7Measurements
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
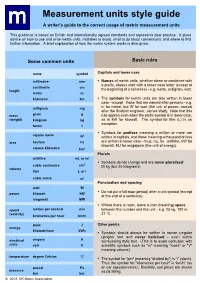
Measurement Units Style Guide a Writer’S Guide to the Correct Usage of Metric Measurement Units
Measurement units style guide A writer’s guide to the correct usage of metric measurement units This guidance is based on British and internationally agreed standards and represents best practice. It gives advice on how to use and write metric units, mistakes to avoid, what to do about conversions, and where to find further information. A brief explanation of how the metric system works is also given. Some common units Basic rules name symbol Capitals and lower case millimetre mm Names of metric units, whether alone or combined with a prefix, always start with a lower case letter (except at centimetre cm length the beginning of a sentence) - e.g. metre, milligram, watt. metre m kilometre km The symbols for metric units are also written in lower case - except those that are named after persons - e.g. milligram mg m for metre, but W for watt (the unit of power, named after the Scottish engineer, James Watt). Note that this mass gram g rule applies even when the prefix symbol is in lower case, (weight) kilogram kg as in kW for kilowatt. The symbol for litre (L) is an exception. tonne t Symbols for prefixes meaning a million or more are square metre 2 m written in capitals, and those meaning a thousand or less area hectare ha are written in lower case - thus, mL for millilitre, kW for kilowatt, MJ for megajoule (the unit of energy). square kilometre km 2 Plurals millilitre mL or ml Symbols do not change and are never pluralised : 3 cubic centimetre cm 25 kg (but 25 kilograms) volume litre L or l cubic metre m3 Punctuation and spacing watt W Do not put a full stop (period) after a unit symbol (except power kilowatt kW at the end of a sentence). -

The Square Kilometre Array (SKA) Will Be an I
INVITED PAPER TheSquareKilometreArray This telescope, to be the largest in the world, will probe the evolution of black holes as well as the basic properties, birth and death of the Universe. By Peter E. Dewdney, Peter J. Hall, Richard T. Schilizzi, and T. Joseph L. W. Lazio ABSTRACT | The Square Kilometre Array (SKA) will be an I. INTRODUCTION ultrasensitive radio telescope, built to further the understand- Advances in astronomy over the past decades have brought ing of the most important phenomena in the Universe, the international community to the verge of charting a including some pertaining to the birth and eventual death of complete history of the Universe. In order to achieve this the Universe itself. Over the next few years, the SKA will make goal, the world community is pooling resources and ex- the transition from an early formative to a well-defined design. pertise to design and construct powerful observatories that This paper outlines how the scientific challenges are translated will probe the entire electromagnetic spectrum, from radio to into technical challenges, how the application of recent gamma-rays, and even beyond the electromagnetic spectrum, technology offers the potential of affordably meeting these studying gravitational waves, cosmic rays, and neutrinos. challenges, and how the choices of technology will ultimately The Square Kilometre Array (SKA) will be one of these be made. The SKA will be an array of coherently connected telescopes, a radio telescope with an aperture of up to a antennas spread over an area about 3000 km in extent, with an million square meters. The SKA was formulated from the 2 aggregate antenna collecting area of up to 106 m at centimeter very beginning as an international, astronomer-led (Bgrass and meter wavelengths. -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -

Land Measurements
© delta alpha publishing MEASUREMENTS LAND LINEAR MEASURE ............................................................ 2 LAND AREA MEASURE ................................................................. 3 VOLUME MEASURE ....................................................................... 4 WEIGHT or MASS ............................................................................ 5 MEASURES OF ANGLES AND ARCS ......................................... 6 AREAS AND VOLUME CALCULATIONS ................................... 6 1 back to the top http://realestatedefined.com © delta alpha publishing LAND LINEAR MEASURE Imperial/US measurements 12 inches (in or ”) = 1 foot (ft or ’) 3 feet = 1 yard (yd) 1,760 yards = 1 mile (mi) = 5,280 feet =320 rods 5½ yards = 1 rod (rd), pole or perch = 16½ feet 40 rods = 1 furlong (fur) = 220 yards 22 yards = 1 chain = 4 rods, poles or perches 220 yards = 10 chains = 1 furlong 8 furlongs = 1 mile = 80 chains 1,852 meters =1 nautical mile = 6,076.115 feet (approx.) Surveying Measurements 7.92 inches = 1 link (li) (Gunter’s or surveyor’s chain) = 0.66 foot 100 links = 1 chain (ch) = 4 rods = 66 feet 80 chains = 1 statute mile (mi.) = 320 rods = 5,280 feet 12 inches = 1 link (Engineer’s chain) 100 links = 1 chain = 100 feet 52.8 chains = 1 mile = 5,280 feet Metric measurements 10 millimetres (mm) = 1 centimetre (cm) 10 centimetres = 1 decimetre (dm) 10 decimetres = 1 meter(AmE)/metre(BrE) = 1,000 millimetres 10 metres = 1 decametre/dekametre (dam) 10 decametres = 1 hectometre (hm) = 100 metres 1,000 metres = 1 kilometre (km) 10,000 metres = 10 kilometres = 1 myriametre Imperial/US to Metric Conversion 0.3937 inches = 1 centimetre (cm) 39.37 inches = 1 metre 3.28084 feet = 1 metre (m) 1.0936 yards = 1 meter(AmE)/metre(BrE) 0.621371 miles = 1 kilometre (km) 2.5400 centimetres = 1 inch 0.3048 metres = 1 foot 0.9144 metres = 1 yard 1.609344 kilometres = 1 mile 2 back to the top http://realestatedefined.com © delta alpha publishing LAND AREA MEASURE Imperial/US measurements 1 square inch (sq. -

KS2 Converting Units
Measurement… @whisto_maths Converting Units What do I need to be able to do? Keywords By the end of this unit you should be able Length: the distance from one point to another to: Mass: a measure of how much matter is in an object. • Recognise metric measures Capacity: the amount an object can contain (normally liquids) • Convert metric measures • Calculate with metric measures Volume: the amount of 3-dimensional space an object takes up (units of length cubed) • Understand Miles and Kilometre Convert: to change a value or expression from one value to another. relationships Imperial: a system of weights and measures originally developed in England. • Recognise Imperial measures and Metric: a system of measuring that replaced the imperial system to fall in line with the rest of Europe. conversions Proportion: values of two items that increase in the same ratio Metric measures Metric conversions Length Common units of length or distance are Length ÷ 10 ÷ 100 ÷ 1000 Millimetres (mm) – “Milli” prefix means one thousandth or ÷ 1000 mm cm m km Centimetres (cm) – “Centi” prefix means one hundredth or ÷ 100 Average height of Metres (m) a man is 2m Kilometres (km) – “Kilo” prefix means a thousand ×1000 Mass × 10 × 100 × 1000 ÷ 1000 ÷ 1000 Mass (Weight) Average weight of g kg t Grams (g) an apple is 100g Kilograms (kg) – “Kilo” prefix means a thousand ×1000 Tonnes (t) × 1000 × 1000 Capacity ÷ 1000 Capacity Average bottle of Milli – thousandth water holds 500ml l Millilitre (ml) - “Milli” prefix means one thousandth or ÷ 1000 ml Centi – hundredth Litre (l) Kilo - thousand × 1000 ÷ 1000 Calculations tips: Metric calculations The final weight is in grams g kg • Do all calculations in the same unit (often A package weighs 350g. -

Measuring the World Music and Lyrics by Graeme Thompson
Mathematical Melodies Measuring the World Music and Lyrics by Graeme Thompson Measuring the World A foot has 12 inches A foot has 5 toes A foot has 30 centimeters As your ruler knows 1 foot 12 inches 30 centimeters ruler knows We’re measuring the world Your little pinkie finger Is a centimeter wide A meter has one hundred centimeters stored inside 1 meter one hundred centimeters all a pinkie wide We’re measuring the world A kilometer is one thousand Meters laid out straight We use them when the distance We are measuring is great 1 kilometer is 1000 meters laid out side by side We’re measuring the world A millimeters less than A centimeter long 10 millimeters And your centimeters strong 10 millimeters are a centimeter long We’re measuring the world Measuring the World 1 Measuring the World Junior: Grade 5 and Grade 6 The Big Ideas Curriculum Connections Measurement Teaching metric conversion Measurement Relationships can be particularly tricky. Grade 5 • select and justify the most appropriate Creating opportunities for standard unit (i.e., millimetre, students to practice purposeful conversion is centimetre, decimetre, metre, kilometre) to the key. Helping students engage through measure length, activities that are meaningful and encourage height, width, and decision making around picking which unit to distance, and to measure the perimeter use in a reasonable way is helpful. Pointing of various polygons; out common or practical uses for metric • solve problems requiring conversion from metres to centimetres and conversion in the students‘ daily lives from kilometres to metres (Sample encourages problem solving and reinforces a problem: Describe the multiplicative relevant personal connection. -

13 the Rhetoric and Politics of Standardization: Measurements and Needs for Precision
13 The rhetoric and politics of standardization: Measurements and needs for precision Important then to escape the pitfalls of any arbitrariness in understanding what we are doing in counting units of length, weight, or any measurements of areas of space, we need to understand what constitutes the unit of measurement in order to use it practically in what we do when we use measuring tools. Measurements such as sums of units of length, area, of volume, angles, weight, and even sums of units of time are countable. In turn we use these measurements to relate to other things that we also define as being countable. How we relate to those countable applications depends upon the measuring tools we create. And what constitutes a unit of measurement is established with these measuring tools within the legal frameworks of what might be considered political power or law, whether laws of the tribe or the sovereign power of a nation. As experts we make political demands that become commands of those that have the political power to standardize measurements in manufacturing, construction, trade, and commerce. They create the law that underpins the technical definitional agreements that are made about measurements by those different social institutional agreements made between social corporate structures and government agencies. Measurements are always made then within certain social and political frameworks. The definitions of measurable units are usually initiated within the jurisdictions of technological and scientific institutions which with their persuasive power are able to eventually reach their legitimized agreements about standards, and they gain their approvable within law using enforceable legal contracts. -
Linear Measures: the Metric System
Units of Measurement: A. The Imperial System Canada uses the metric system – most of the time! However, there are still places and occasions where the imperial system of measurement is used. People often talk about their height in feet and inches or their weight in pounds. Many recipes measure in cups and teaspoons. Another example is the term ‘two by four’ when talking about lumber. That term means that a plank is roughly two inches thick and four inches wide. Another place where the imperial system of measurement is often seen is in the grocery store, especially in the meat/fish and fresh produce sections. Prices and weights are often given in both metric and imperial units of measurement. For example, you may see a sign advertising “Potatoes – 89¢ a pound (lb.) or $1.96 per kilogram (kg)”. The USA uses only a system of measurement related to the imperial one, so items imported from there often do not have a metric equivalent given. Cookbooks frequently use one or the other system of measurement. For all these reasons, it is important to understand both systems and be able to convert one into the other. The most common imperial units of measurement are: Quantity Unit Symbol length foot ft. weight pound lb. volume gallon gal. Here are the most common conversions of imperial units of measurement: Length Weight Volume 1 foot (ft. ) = 12 inches (in.) 1 pound (lb.) = 16 ounces (oz.) 1 pint (pt.) = 2 cups 1 yard (yd.) = 3 feet 1 ton = 2000 pounds (lbs.) 1 quart (qt.) = 2 pints 1 mile (mi.) = 5280 feet or 1760 yards 1 gallon (gal.) = 4 quarts When we convert units in the imperial system, we use a familiar rule: When we convert a larger unit to a smaller unit, we multiply by the conversion factor. -

Engilab Units 2018 V2.2
EngiLab Units 2021 v3.1 (v3.1.7864) User Manual www.engilab.com This page intentionally left blank. EngiLab Units 2021 v3.1 User Manual (c) 2021 EngiLab PC All rights reserved. No parts of this work may be reproduced in any form or by any means - graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems - without the written permission of the publisher. Products that are referred to in this document may be either trademarks and/or registered trademarks of the respective owners. The publisher and the author make no claim to these trademarks. While every precaution has been taken in the preparation of this document, the publisher and the author assume no responsibility for errors or omissions, or for damages resulting from the use of information contained in this document or from the use of programs and source code that may accompany it. In no event shall the publisher and the author be liable for any loss of profit or any other commercial damage caused or alleged to have been caused directly or indirectly by this document. "There are two possible outcomes: if the result confirms the Publisher hypothesis, then you've made a measurement. If the result is EngiLab PC contrary to the hypothesis, then you've made a discovery." Document type Enrico Fermi User Manual Program name EngiLab Units Program version v3.1.7864 Document version v1.0 Document release date July 13, 2021 This page intentionally left blank. Table of Contents V Table of Contents Chapter 1 Introduction to EngiLab Units 1 1 Overview .................................................................................................................................. -
Sg4-Units-Of-Measurement.Pdf
Units of Measurement: A. The Imperial System Canada uses the metric system – most of the time! However, there are still places and occasions where the imperial system of measurement is used. People often talk about their height in feet and inches or their weight in pounds. Many recipes measure in cups and teaspoons. Another example is the term ‘two by four’ when talking about lumber. That term means that a plank is roughly two inches thick and four inches wide. Another place where the imperial system of measurement is often seen is in the grocery store, especially in the meat/fish and fresh produce sections. Prices and weights are often given in both metric and imperial units of measurement. For example, you may see a sign advertising “Potatoes – 89¢ a pound (lb.) or $1.96 per kilogram (kg)”. The USA uses only a system of measurement related to the imperial one, so items imported from there often do not have a metric equivalent given. Cookbooks frequently use one or the other system of measurement. For all these reasons, it is important to understand both systems and be able to convert one into the other. The most common imperial units of measurement are: Quantity Unit Symbol length foot ft. weight pound lb. volume gallon gal. Here are the most common conversions of imperial units of measurement: Length Weight Volume 1 foot (ft. ) = 12 inches (in.) 1 pound (lb.) = 16 ounces (oz.) 1 pint (pt.) = 2 cups 1 yard (yd.) = 3 feet 1 ton = 2000 pounds (lbs.) 1 quart (qt.) = 2 pints 1 mile (mi.) = 5280 feet or 1760 yards 1 gallon (gal.) = 4 quarts When we convert units in the imperial system, we use a familiar rule: When we convert a larger unit to a smaller unit, we multiply by the conversion factor. -

Units of Measurement to Be Used in Air and Ground Operations
International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices,see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Suzanne TRANSMITTAL NOTE NEW EDITIONS OF ANNEXES TO THE CONVENTION ON INTERNATIONAL CIVIL AVIATION It has come to our attention that when a new edition of an Annex is published, users have been discarding, along with the previous edition of the Annex, the Supplement to the previous edition. Please note that the Supplement to the previous edition should be retained until a new Supplement is issued. Suzanne International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations ________________________________ This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices, see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Published in separate English, Arabic, Chinese, French, Russian and Spanish editions by the INTERNATIONAL CIVIL AVIATION ORGANIZATION 999 University Street, Montréal, Quebec, Canada H3C 5H7 For ordering information and for a complete listing of sales agents and booksellers, please go to the ICAO website at www.icao.int First edition 1948 Fourth edition 1979 Fifth edition 2010 Annex 5, Units of Measurement to be Used in Air and Ground Operations Order Number: AN 5 ISBN 978-92-9231-512-2 © ICAO 2010 All rights reserved. -

Measurements and Symbols Used in Plumbing 27
Measurements and 4 Symbols used in Plumbing INTRODUCTION In the previous Units, we have covered plumbing tools, material and pipes. Besides knowing the benefits and suitability of material in various tasks, a plumber must also be efficient in measurement of plumbing material with the help of measurement tools and be able to manage conversion of units easily. Similarly, a plumber should also be able to understand and read the various symbols used in plumbing drawings. Plumbing material is needed as per the requirement of the plumbing work to be done and its plan. Plumbing fitting and fixtures are available in the market in different sizes and types. The size of the plumbing items can vary from inch to feet and metre in height. Plumbing items are also available as per volumetric capacity like water tanks, storage and flush tank, etc. Knowledge of various dimensions and sizes of plumbing items is crucial in the proper selection and purchasing of plumbing material in the market. Unit 4.indd 26 8/7/2018 11:06:08 AM Fig. 4.1: Measuring scale MEASUREMENT OF LENGTH A plumber uses the metallic tape, cloth tape, scale and foot rule for measuring. Metallic tape should be used for accuracy in the measurement. Metre and its divisions are printed on the measuring tape. The symbol of feet is (′) and the symbol of inch is (″). For example, the meaning of 4′-9″ is four feet nine inches. Both the systems, i.e., metric system and FPS (Foot-Pound-Second) system are used in plumbing measurement. (a) In metric systems 1 metre = 10 decimetre (dm) 1 metre =