Measuring Length

Total Page：16

File Type：pdf, Size：1020Kb

05-NelsonMathGr6-Chap05 7/18/05 4:39 PM Page 142 CHAPTER 5 1 Measuring Length Goal Select an appropriate measuring unit. James’s family went to Lighthouse Park in West Vancouver. The park has many very old and tall ﬁr, cedar, and arbutus trees. James tried to decide which unit he would use to measure the trip and everything he saw. He thinks he can use decametres to measure the length of a path around the base of this tree. ? What units of length are appropriate for describing their trip? decametre (dam) James’s Comparison A unit of measurement for length 1 dam ϭ 10 m Dad stood next to a young tree that is just about as tall as he is. Dad’s height is 195 cm. A. What unit would you use to describe the height of the older trees in the park? Explain your choice. B. What unit would you use to describe the distance James’s family travelled to get to Lighthouse Park? Why? C. James picked up a piece of bark from a fallen arbutus tree. The bark is known for being very thin. What unit would you use to describe its thickness? D. What unit would you use to describe the thickness of a cedar leaf? E. What other things in a West Coast rain forest might be measured in the same units as your answer to Part D? 142 NEL 05-NelsonMathGr6-Chap05 7/18/05 4:39 PM Page 143 Reflecting 1. Why did all of the units you chose include “metre”? 2. Suppose a leaf was 7.2 cm long. Why can you say that it had been measured to the nearest millimetre? 3. Why are different units appropriate for different measurements? Checking 4. Select an appropriate unit for each measurement. Explain each choice. a) the height of a room b) the thickness of a window c) the distance across your town or city Practising 5. A nursery is selling young trees. What units are appropriate for these measurements? Explain. a) the heights of the trees b) the lengths of the leaves of the trees 6. For which measurements are centimetres appropriate? Explain. a) the thickness of your math book b) the thickness of your ﬁngernail c) the thickness of 100 sheets of paper 7. Why might you measure the thickness of a wire in millimetres rather than centimetres? 8. Ryan is in a video store. What items in the store, if any, might be measured in these units? a) millimetres c) metres b) centimetres d) kilometres 9. Is it likely that a tall building would be measured in kilometres? Explain. 10. A decimetre is 0.1 metre. A decametre is 10 m. What might be the name of the unit between decametres and kilometres? Explain. NEL 143.

Copy Link

Recommended publications

Standard Caption Abberaviation
TECHNICAL SHEET Page 1 of 2 STANDARD CAPTION ABBREVIATIONS Ref: T120 – Rev 10 – March 02 The abbreviated captions listed are used on all instruments except those made to ANSI C39. 1-19. Captions for special scales to customers’ requirements must comply with BS EN 60051, unless otherwise specified at time of ordering. * DENOTES captions applied at no extra cost. Other captions on request. ELECTRICAL UNITS UNIT SYMBOL UNIT SYMBOL Direct Current dc Watt W * Alternating current ac Milliwatts mW * Amps A * Kilowatts kW * Microamps µA * Megawatts MW * Milliamps mA * Vars VAr * Kiloamps kA * Kilovars kVAr * Millivolts mV * Voltamperes VA * Kilovolts kV * Kilovoltamperes kVA * Cycles Hz * Megavoltamperes MVA * Power factor cos∅ * Ohms Ω * Synchroscope SYNCHROSCOPE * Siemens S Micromhos µmho MECHANICAL UNITS Inches in Micrometre (micron) µm Square inches in2 Millimetre mm Cubic inches in3 Square millimetres mm2 Inches per second in/s * Cubic millimetres mm3 Inches per minute in/min * Millimetres per second mm/s * Inches per hour in/h * Millimetres per minute mm/min * Inches of mercury in hg Millimetres per hour mm/h * Feet ft Millimetres of mercury mm Hg Square feet ft2 Centimetre cm Cubic feet ft3 Square centimetres cm2 Feet per second ft/s * Cubic centimetres cm3 Feet per minute ft/min * Cubic centimetres per min cm3/min Feet per hour ft/h * Centimetres per second cm/s * Foot pound ft lb Centimetres per minute cm/min * Foot pound force ft lbf Centimetres per hour cm/h * Hours h Decimetre dm Yards yd Square decimetre dm2 Square yards yd2 Cubic
[Show full text]
Perri Et Al. 2015. Sedimentary and Thermal Evolution of The
See discussions, stats, and author profiles for this publication at: http://www.researchgate.net/publication/270824977 Sedimentary and thermal evolution of the Eocene-Oligocene mudrocks from the southwestern Thrace Basin (NE Greece) ARTICLE in BASIN RESEARCH · JANUARY 2015 Impact Factor: 2.73 · DOI: 10.1111/bre.12112 CITATION READS 1 99 7 AUTHORS, INCLUDING: Francesco Perri Salvatore Critelli Università della Calabria Università della Calabria 54 PUBLICATIONS 469 CITATIONS 157 PUBLICATIONS 1,723 CITATIONS SEE PROFILE SEE PROFILE Francesco Muto Rocco Dominici Università della Calabria Università della Calabria 45 PUBLICATIONS 266 CITATIONS 46 PUBLICATIONS 173 CITATIONS SEE PROFILE SEE PROFILE Available from: Salvatore Critelli Retrieved on: 19 November 2015 EAGE Basin Research (2015) 1–21, doi: 10.1111/bre.12112 Sedimentary and thermal evolution of the Eocene- Oligocene mudrocks from the southwesternThrace Basin (NEGreece) F. Perri,* L. Caracciolo,† F. Cavalcante,‡ S. Corrado,§ S. Critelli,* F. Muto* and R. Dominici* *Dipartimento di Biologia, Ecologia e Scienze della Terra, Universita della Calabria, Rende (CS), Italy †Chemostrat Ltd., Sandtrak Unit, Ravenscroft Court, Buttington Cross Enterpise, Welshpool, UK ‡CNR – Istituto di Metodologie per l’Analisi Ambientale, Tito Scalo (PZ), Italy §Dipartimento di Scienze, Sezione di Scienze Geologiche, Universita degli Studi “Roma Tre”, Roma, Italy ABSTRACT Paleothermal indicators based on clay mineral and organic matter analyses, were integrated with mudrock geochemistry and stratigraphic data to deﬁne the sedimentary evolution of the southwest- ern Thrace Basin during the Eocene to Oligocene. This multi-method approach allowed us to recon- struct the burial evolution of the basin in Eocene and Oligocene times and to study the mudrock composition and relate this to their provenance and source area weathering.
[Show full text]
Using Integrated Experiments and Mathematical Modeling to Upscale Biotic Weathering Processes from Pore to Field and Global Scales
Poster presentation EGU2011-7118 – EGU General Assembly 2011, Vienna, 6th April 2011 Using integrated experiments and mathematical modeling to upscale biotic weathering processes from pore to field and global scales Jonathan Bridge*, Steven Banwart, and the NERC Weathering Science Consortium Team 1 Kroto Research Institute, The University of Sheffield, Sheffield, United Kingdom. * presenting author Summary Conceptual model: from nanoscale Mineral weathering at hyphae interfaces Figure 1 Soil mycorrhizal fungi act through chemical interactions at nanometer scale to dissolve weathering to global scale systems Section 1 • Minerals incubated in controlled microcosms with minerals, and transport weathering products to plant symbionts through metre scale Pinus sylvestris – Paxillus involutus (3-6 months) 2 cm mycelial networks at diurnal timescales [1]. Biologically-mediated soil development Section 2 • NANOSingle hypha on biotite identified and sectioned to occurs at regional scale over millenia (ka) and coupling between ecological, geological analyse sub-interface mineral composition profiles Studied and atmospheric systems is apparent over evolutionary (Ma) timescales [2]. Our hypha • Removal of K, Al, Mg, Fe over 72 day contact time hypothesis is that quantification of biologically-driven weathering reactions at Section 3 • Model fits data by diffusion-controlled hydrated molecular scale provides a basis for new conceptual approaches to processes such as soil Growth layer formation and release of ions from lattice direction • Significant new dry soil weathering process formation and atmospheric CO2 evolution that occur over much larger temporal and 100 μm spatial scales. A reaction-diffusion model based Section 4 B on ion-exchange release of K+ by To test this we have applied an integrated suite of observations at scales from nanometre Biotite chips exposed to EM fungi in microscosms protons fits depth profiles and to decimetre using common minerals, fungi and physical and chemical conditions.
[Show full text]
It's a Nano World
IT’S A NANO WORLD Learning Goal • Nanometer-sized things are very small. Students can understand relative sizes of different small things • How Scientists can interact with small things. Understand Scientists and engineers have formed the interdisciplinary field of nanotechnology by investigating properties and manipulating matter at the nanoscale. • You can be a scientist DESIGNED FOR C H I L D R E N 5 - 8 Y E A R S O L D SO HOW SMALL IS NANO? ONE NANOMETRE IS A BILLIONTH O F A M E T R E Nanometre is a basic unit of measurement. “Nano” derives from the Greek word for midget, very small thing. If we divide a metre by 1 thousand we have a millimetre. One thousandth of a millimetre is a micron. A thousandth part of a micron is a nanometre. MACROSCALE OBJECTS 271 meters long. Humpback whales are A full-size soccer ball is Raindrops are around 0.25 about 14 meters long. 70 centimeters in diameter centimeters in diameter. MICROSCALE OBJECTS The diameter of Pollen, which human hairs ranges About 7 micrometers E. coli bacteria, found in fertilizes seed plants, from 50-100 across our intestines, are can be about 50 micrometers. around 2 micrometers micrometers in long. diameter. NANOSCALE OBJECTS The Ebola virus, The largest naturally- which causes a DNA molecules, which Water molecules are occurring atom is bleeding disease, is carry genetic code, are 0.278 nanometers wide. uranium, which has an around 80 around 2.5 nanometers atomic radius of 0.175 nanometers long. across. nanometers. TRY THIS! Mark your height on the wall chart.
[Show full text]
Solar Decimetre Radio Bursts
SOLAR DECIMETRE RADIO BURSTS By R. F. MULLALy*t and T. KRISHNAN* [Manuscript recewed September 20, 1962] Summary High resolution studies (2' of arc beam) were made with the east·west arm of the Christiansen radio interferometer for about 50 21·cm solar burst events during 1958-1961. The burst sources were always closely associated in position with already existing radio plage regions of the Sun's slowly varying decimetre radiation. They had sizes of from 2 to 5' of arc, never exceeded but often approached in size their parent plage region, and showed no major movements during their development. Brightness temperatures ranged up to 2 X 109 OK (mostly between 107 and 108 OK). More bursts were observed near the Sun's centre than near the limb, and more on the western than on the eastern half. There was also a curious "gap" of 30° longitude on the eastern half of the Sun with virtually no burst activity. 1. INTRODUCTION A solar decimetre radio burst is part of a complex of simultaneous or closely successive events which may extend from optical to metre wavelengths in the electromagnetic spectrum, and sometimes involve the ejection of corpuscular streams. The characteristics of burst emission in different frequency ranges differ markedly. Further, in the same frequency range burst sources of different types may be distinguished. The basic observations required to delineate radio-frequency bursts comprise dynamic spectra, showing the variation in intensity of emission as a function of both frequency and time; and high resolution studies of the position, size, shape, movement, and brightness temperature of the emitting region.
[Show full text]
Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre
[Show full text]
Measuring the World Music and Lyrics by Graeme Thompson
Mathematical Melodies Measuring the World Music and Lyrics by Graeme Thompson Measuring the World A foot has 12 inches A foot has 5 toes A foot has 30 centimeters As your ruler knows 1 foot 12 inches 30 centimeters ruler knows We’re measuring the world Your little pinkie ﬁnger Is a centimeter wide A meter has one hundred centimeters stored inside 1 meter one hundred centimeters all a pinkie wide We’re measuring the world A kilometer is one thousand Meters laid out straight We use them when the distance We are measuring is great 1 kilometer is 1000 meters laid out side by side We’re measuring the world A millimeters less than A centimeter long 10 millimeters And your centimeters strong 10 millimeters are a centimeter long We’re measuring the world Measuring the World 1 Measuring the World Junior: Grade 5 and Grade 6 The Big Ideas Curriculum Connections Measurement Teaching metric conversion Measurement Relationships can be particularly tricky. Grade 5 • select and justify the most appropriate Creating opportunities for standard unit (i.e., millimetre, students to practice purposeful conversion is centimetre, decimetre, metre, kilometre) to the key. Helping students engage through measure length, activities that are meaningful and encourage height, width, and decision making around picking which unit to distance, and to measure the perimeter use in a reasonable way is helpful. Pointing of various polygons; out common or practical uses for metric • solve problems requiring conversion from metres to centimetres and conversion in the students‘ daily lives from kilometres to metres (Sample encourages problem solving and reinforces a problem: Describe the multiplicative relevant personal connection.
[Show full text]
13 the Rhetoric and Politics of Standardization: Measurements and Needs for Precision
13 The rhetoric and politics of standardization: Measurements and needs for precision Important then to escape the pitfalls of any arbitrariness in understanding what we are doing in counting units of length, weight, or any measurements of areas of space, we need to understand what constitutes the unit of measurement in order to use it practically in what we do when we use measuring tools. Measurements such as sums of units of length, area, of volume, angles, weight, and even sums of units of time are countable. In turn we use these measurements to relate to other things that we also define as being countable. How we relate to those countable applications depends upon the measuring tools we create. And what constitutes a unit of measurement is established with these measuring tools within the legal frameworks of what might be considered political power or law, whether laws of the tribe or the sovereign power of a nation. As experts we make political demands that become commands of those that have the political power to standardize measurements in manufacturing, construction, trade, and commerce. They create the law that underpins the technical definitional agreements that are made about measurements by those different social institutional agreements made between social corporate structures and government agencies. Measurements are always made then within certain social and political frameworks. The definitions of measurable units are usually initiated within the jurisdictions of technological and scientific institutions which with their persuasive power are able to eventually reach their legitimized agreements about standards, and they gain their approvable within law using enforceable legal contracts.
[Show full text]
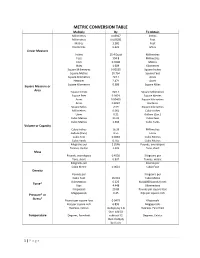
Metric Conversion Table
METRIC CONVERSION TABLE Multiply By To Obtain Millimetres 0.03937 Inches Millimetres 0.003281 Feet Metres 3.281 Feet Kilometres 0.621 Miles Linear Measure Inches 25.4 Exact Millimetres Feet 304.8 Millimetres Feet 0.3048 Metres Miles 1.609 Kilometres Square Millimetres 0.00155 Square Inches Square Metres 10.764 Square Feet Square Kilometres 247.1 Acres Hectares 2.471 Acres Square Kilometres 0.386 Square Miles Square Measure or Area Square Inches 645.2 Square Millimetres Square Feet 0.0929 Square Metres Acres 0.00405 Square Kilometres Acres 0.4047 Hectares Square Miles 2.59 Square Kilometres Millimetres 0.061 Cubic Inches Litres 0.22 Gallons (Can.) Cubic Metres 35.31 Cubic Feet Cubic Metres 1.308 Cubic Yards Volume or Capacity Cubic Inches 16.39 Millimetres Gallons (Can.) 4.55 Litres Cubic Feet 0.0283 Cubic Metres Cubic Yards 0.765 Cubic Metres Kilograms per 2.2046 Pounds, avoirdupois Tonnes, metric 1.102 Tons, short Mass Pounds, avoirdupois 0.4536 Kilograms per Tons, short 0.907 Tonnes, metric Kilograms per Pounds per Cubic Metre 0.0624 Cubic Foot Density Pounds per Kilograms per Cubic Foot 16.019 Cubic Metre Kilonewtons 0.225 Kips(1000 ponds force) Force* Kips 4.448 Kilonewtons Kilopascals 20.89 Pounds per square foot Megapascals 0.45 Kips per square inch Pressure* or Stress* Pounds per square foot 0.0479 Kilopascals Kips per square inch 6.895 Megapascals Degrees, Celsius multiply by 1.8 Degrees, Farenheit then add 32 Temperature Degrees, Farenheit subtract 32 Degrees, Celsius then multiply by 0.555 1 | P a g e METRIC CONVERSION GUIDE Linear Measurement One millimetre (1 mm) is equal to a thousandth part of a metre (0.001 m) and is a little greater than 1/32”.
[Show full text]
1.0 GENERAL 1.1 Abbreviation/Symbol Meaning Μm Micrometre Or Micron Mm Millimetre M Metre Mm Or Mm2 Square Millimetre M Or M2 S
Section 01275 Alberta Transportation Measurement Rules Tender No. [ ] Page 1 1.0 GENERAL 1.1 MEASUREMENT SYSTEM .1 This section specifies the measurement rules that will generally be used for payment purposes unless otherwise specified in the Contract Documents. In case of conflict between the method of measurement specified in this section and the requirements specified in Section 01280 – Measurement Schedule, the latter will govern. .2 Work will be measured in the International System of Units (SI) in accordance with CAN/CSA–Z234.1–89 Canadian Metric Practice Guide. .3 When used in the Contract, the following abbreviations and symbols have the meaning assigned to them. Abbreviation/Symbol Meaning µm micrometre or micron mm millimetre m metre mm2 or mm2 square millimetre m2 or m2 square metre ha hectare kPa kilopascal MPa megapascal m3 or m3 cubic metre l (or where clarity is needed L) litre L.S. lump sum g gram kg kilogram N newton kN kilonewton t tonne no. number (quantity) min minute (time) h hour d day wk week % percent > greater than greater than or equal to < less than less than or equal to $ Canadian dollars ° degree (angle) °C degree Celsius Section 01275 Alberta Transportation Measurement Rules Tender No. [ ] Page 2 1.2 METHOD OF MEASUREMENT .1 Unless otherwise indicated in the Contract Documents: .1 earthwork materials will be measured net in place after compaction, with no allowance for bulking, shrinkage, compression, foundation settlement, or waste; .2 products will be measured net, with no allowance for waste; .3 dimensions used in calculating quantities will be rounded to the nearest unit of dimension as follows: Quantity Dimension [Volume of earth centimetre Volume of concrete millimetre Length of pipe centimetre Area of land decimetre [ ] [ ]] .4 the survey [station line] [station grid] system adopted will be at [10] [15] [20] [30] [100] linear metres spacing for measuring [ ], respectively; .5 contours may be based on aerial photograph interpretation and are approximate only.
[Show full text]
Linear Measures: the Metric System
Units of Measurement: A. The Imperial System Canada uses the metric system – most of the time! However, there are still places and occasions where the imperial system of measurement is used. People often talk about their height in feet and inches or their weight in pounds. Many recipes measure in cups and teaspoons. Another example is the term ‘two by four’ when talking about lumber. That term means that a plank is roughly two inches thick and four inches wide. Another place where the imperial system of measurement is often seen is in the grocery store, especially in the meat/fish and fresh produce sections. Prices and weights are often given in both metric and imperial units of measurement. For example, you may see a sign advertising “Potatoes – 89¢ a pound (lb.) or $1.96 per kilogram (kg)”. The USA uses only a system of measurement related to the imperial one, so items imported from there often do not have a metric equivalent given. Cookbooks frequently use one or the other system of measurement. For all these reasons, it is important to understand both systems and be able to convert one into the other. The most common imperial units of measurement are: Quantity Unit Symbol length foot ft. weight pound lb. volume gallon gal. Here are the most common conversions of imperial units of measurement: Length Weight Volume 1 foot (ft. ) = 12 inches (in.) 1 pound (lb.) = 16 ounces (oz.) 1 pint (pt.) = 2 cups 1 yard (yd.) = 3 feet 1 ton = 2000 pounds (lbs.) 1 quart (qt.) = 2 pints 1 mile (mi.) = 5280 feet or 1760 yards 1 gallon (gal.) = 4 quarts When we convert units in the imperial system, we use a familiar rule: When we convert a larger unit to a smaller unit, we multiply by the conversion factor.
[Show full text]
Engilab Units 2018 V2.2
EngiLab Units 2021 v3.1 (v3.1.7864) User Manual www.engilab.com This page intentionally left blank. EngiLab Units 2021 v3.1 User Manual (c) 2021 EngiLab PC All rights reserved. No parts of this work may be reproduced in any form or by any means - graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems - without the written permission of the publisher. Products that are referred to in this document may be either trademarks and/or registered trademarks of the respective owners. The publisher and the author make no claim to these trademarks. While every precaution has been taken in the preparation of this document, the publisher and the author assume no responsibility for errors or omissions, or for damages resulting from the use of information contained in this document or from the use of programs and source code that may accompany it. In no event shall the publisher and the author be liable for any loss of profit or any other commercial damage caused or alleged to have been caused directly or indirectly by this document. "There are two possible outcomes: if the result confirms the Publisher hypothesis, then you've made a measurement. If the result is EngiLab PC contrary to the hypothesis, then you've made a discovery." Document type Enrico Fermi User Manual Program name EngiLab Units Program version v3.1.7864 Document version v1.0 Document release date July 13, 2021 This page intentionally left blank. Table of Contents V Table of Contents Chapter 1 Introduction to EngiLab Units 1 1 Overview ..................................................................................................................................
[Show full text]