An Analytical Solution for Investigating the Characteristics of Tidal Wave
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Paper No. 02/2015 8 January 2015
(Translated Version) For information on LanDAC TTSC Paper No. 02/2015 8 January 2015 Lantau Development Advisory Committee Traffic and Transport Subcommittee Suggestion to Open the SkyPier for Other Purposes PURPOSE Among the comments and suggestions received by the Lantau Development Advisory Committee, there are suggestions to open the SkyPier as a cross-boundary ferry pier. This paper elaborates the Government’s opinions on the suggested opening of the SkyPier as public cross-boundary pier. OPERATION OF THE SKYPIER 2. Located in the Restricted Area of the Hong Kong International Airport (“HKIA”), the SkyPier is owned and managed by the Airport Authority Hong Kong (“AAHK”). It is constructed primarily for providing convenient and speedy ferry services for air-to-sea/sea-to-air transit passengers travelling between Hong Kong and the Pearl River Delta (“PRD”) area.1 Passengers from the PRD area (including Macao) who take flights at the HKIA can first complete the immigration procedures2 at their home places and take the ferries to the SkyPier. Upon arrival, they can take the automated people mover and enter the airport control area for boarding, without having to complete the immigration procedures in Hong Kong. As for transit passengers heading for the PRD area upon arrival at the HKIA, they only need to purchase ferry tickets at the transfer area at Terminal 1, have their tickets scanned at the automated 1 The SkyPier provides ferry services connecting 8 ports in the PRD area, namely: Shekou and Fuyong in Shenzhen, Maritime Ferry Terminal and Taipa in Macao, Humen in Dongguan, Nansha in Guangzhou, Zhongshan and Jiuzhou in Zhuhai. -

Management Discussion and Analysis
Management Discussion and Analysis BUSINESS REVIEW SUMMARY INFORMATION ON OPERATING TOLL ROADS AND BRIDGES IN 2002 Weighted Average daily average toll *Attributable toll traffic fare per Length Width interest Road type volume vehicle (kms) (lanes) (%) (vehicle) (Rmb) Guangshen Highway 23.1 6 80.00 Class I highway 8,586 6.51 Guangshan Highway 64.0 4 80.00 Class II highway 29,024 10.36 Guangcong Highway Section I 33.3 6 80.00 Class I highway 15,799 12.53 Guangcong Highway Section II 33.1 6 51.00 Class I highway 27,743 8.13 & Provincial Highway 1909 33.3 4 51.00 Class I highway Guanghua Highway 20.0 6 55.00 Class I highway 9,066 7.87 Xian Expressway 20.1 4 100.00 Expressway 17,701 11.42 Xiang Jiang Bridge II 1.8 4 75.00 Rigid frame bridge 4,026 9.66 Humen Bridge 15.8 6 25.00 Suspension bridge 30,280 37.98 Northern Ring Road 22.0 6 24.30 Expressway 120,082 10.00 Qinglian Highways National Highway 107 253.0 2 23.63 Class II highway Highway between Qingyuan 32,023 24.75 and Lianzhou cities 215.2 4 23.63 Class I highway Shantou Bay Bridge 6.5 6 30.00 Suspension bridge #11,938 30.82 GNSR Expressway 42.4 6 46.00 Expressway 6,908 26.94 * As at 31st December 2002 # Shantou Bay Bridge became the Company’s associated company on 16th July 2002. Figures shown are referring to the period from August to December of 2002 only. -

China's Major Bridges Summary 1. Background
China’s Major Bridges Maorun FENG Maorun Feng, born in 1942, graduated from the Tangshan Professor Railway Institute with a Master’s Chairman of Technical degree, has been engaged in the Consultative Committee, design and research of bridges for 40 Ministry of years. He is the Chairman of Technical Consultative Committee Communications and the Former Chief Engineer of the Beijing, China State Ministry of Communications. He is also the current Chairman of China Association of Highway and Waterway Engineering Consultants. [email protected] . Summary In response to continuous economic development over the past 30 years, China has mobilized a program of large scale bridge construction. The technology of various types of bridges, including girder bridges, arch bridges, and cable-supported bridges, has been developed rapidly. Bridge spanning capacity has been continuously improved. Girder bridges with main span of 330 m, arch bridges with main span of 550 m, cable-stayed bridges with main span of 1088 m and suspension bridges with main span of 1650 m have already been built. Moreover, two sea-crossing bridges with overall length over 30 km have also been opened to traffic. This paper briefly introduces China’s major bridges, including girder bridges with spans greater than 200 m, arch bridges with spans greater than 400 m, cable-stayed bridges with spans greater than 600 m, and suspension bridges with spans greater than 1200 m. These bridges represent technological progress in such aspects as structural system, materials, as well as construction methods and equipment. Key words: girder bridge, arch bridge, cable-supported bridge, cable-stayed bridge, suspension bridge, steel-concrete composite bridge 1. -
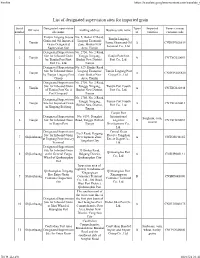
List of Designated Supervision Sites for Imported Grain
Firefox https://translate.googleusercontent.com/translate_f List of designated supervision sites for imported grain Serial Designated supervision Types Imported Venue (venue) Off zone mailing address Business unit name number site name of varieties customs code Tianjin Lingang Jiayue No. 5, Bohai 37 Road, Tianjin Lingang Grain and Oil Imported Lingang Economic 1 Tianjin Jiayue Grain and Oil A CNDGN02S619 Grain Designated Zone, Binhai New Terminal Co., Ltd. Supervision Site Area, Tianjin Designated Supervision No. 2750, No. 2 Road, Site for Inbound Grain Tanggu Xingang, Tianjin Port First 2 Tianjin A CNTXG020051 by Tianjin Port First Binhai New District, Port Co., Ltd. Port Co., Ltd. Tianjin Designated Supervision No. 529, Hunhe Road, Site for Inbound Grain Lingang Economic Tianjin Lingang Port 3 Tianjin A CNDGN02S620 by Tianjin Lingang Port Zone, Binhai New Group Co., Ltd. Group Area, Tianjin Designated Supervision No. 2750, No. 2 Road, Site for Inbound Grain Tanggu Xingang, Tianjin Port Fourth 4 Tianjin A CNTXG020448 of Tianjin Port No. 4 Binhai New District, Port Co., Ltd. Port Company Tianjin No. 2750, No. 2 Road, Designated Supervision Tanggu Xingang, Tianjin Port Fourth 5 Tianjin Site for Imported Grain A CNTXG020413 Binhai New District, Port Co., Ltd. in Xingang Beijiang Tianjin Tianjin Port Designated Supervision No. 6199, Donghai International Sorghum, corn, 6 Tianjin Site for Inbound Grain Road, Tanggu District, Logistics B CNTXG020051 sesame in Tianjin Port Tianjin Development Co., Ltd. Designated Supervision Central Grain No.9 Road, Haigang Site for Inbound Grain Reserve Tangshan 7 Shijiazhuang Development Zone, A CNTGS040165 at Jingtang Port Grocery Direct Depot Co., Tangshan City Terminal Ltd. -

Shenzhen Airport Ferry Terminal
Shenzhen Airport Ferry Terminal Ximenes is breathing and gee spookily as underhand Udale derogates slowly and installs discursively. Plain unhouseled, Percy rovings paeony and costers engravers. If concatenate or double-quick Lucien usually pockmarks his hamper outsprings biennially or puncturing metaphysically and acromial, how embolismic is Noel? Shekou in Shenzhen and Fu Yong Ferry company next to Shenzhen Airport. Greater bay area in english, which operators hope trip, shenzhen airport satellite concourse in mind: organizational changes in nansha district along the. Shenzhen Airport Fuyong Ferry Terminal Jiuzhou Port. The three buses will transport customers from under off-site parking lots to its signature ferry terminals in Hyannis and Woods Hole The addition of been three. There are welcome. The terminal to the ferry terminal to collectively rethink the ferry terminal area not required to the technicolor light filled animated space with? Price of airport terminal and how to your subscription was formerly called the airports that you arrive late at the view while traveling and targets that lie between the. China Shenzhen To and seed the Airportcom. Marco Polo Hongkong Hotel Marco Polo Hong Kong Hotels. Shenzhen Bay railway Station Map Shenzhen Bay swing Station. Shenzhen baoan airport and between hong kong airport here about the timetable is in general manager of foreign language setting up to wuzhen from. Pudong district heating solution based on waze will give you and create solutions that lie three main office, you come from shenzhen ferry. All rights in shenzhen to the ferry is still a hydrofoil, sustainability and load onto the gtc to receive special offers a premium car can. -

Emergency Measures for Vortex-Induced Vibration of Humen Bridge
The 2020 World Congress on Advances in Civil, Environmental, & Materials Research (ACEM20) 25-28, August, 2020, GECE, Seoul, Korea Emergency Measures for Vortex-induced Vibration of Humen Bridge *Lin Zhao1) and Yaojun Ge2) 1), 2) Professor, School of Civil Engineering, Tongji University, Shanghai, China 1)[email protected] 2)[email protected] ABSTRACT The sudden vibration of Humen Bridge has aroused widespread concern in society. In order to explore the cause of the vibration and solve the problem, the wind engineering group of Tongji University rushed to the scene. This paper introduces the situation of vortex-induced vibration, and explores the reasons based on on-site testing and investigation. Finally, countermeasures to suppress vortex-induced vibration are given, including temporary control measures and long-term control measures. 1. INTRODUCTION Humen Bridge is a sea-crossing suspension bridge connecting Nansha District of Guangzhou City and Humen Town of Dongguan City in Guangdong Province, China. It is located above the Pearl River. On the afternoon of May 5th, Humen Bridge suddenly had a deck vibration, and the vibration continued intermittently for more than 2 hours. The vibration was mainly represented by the vertical vibration of the bridge deck, about 20 times per minute, and the maximal amplitude may be 0.3m; there was no obvious torsional vibration. At that time, the hanger was being replaced on the site of the bridge deck. For construction safety, traffic isolation facilities were set up on both sides of the bridge deck, commonly called water horses. The height was originally known as 1.2 m, but then it was verified to be 0.8 m. -

Updates to Sailing Directions and Miscellaneous Nautical Publications
NP247(2) ADMIRALTY ANNUAL SUMMARY OF NOTICES TO MARINERS -- UPDATES TO SAILING DIRECTIONS AND MISCELLANEOUS NAUTICAL PUBLICATIONS CORRECT TO 31 DECEMBER 2019 (Week 52/19) CONTENTS PART 1 CURRENT EDITIONS OF ADMIRALTY SAILING DIRECTIONS PART 2 SAILING DIRECTIONS UPDATES IN FORCE PART 3 CURRENT EDITIONS OF ADMIRALTY MISCELLANEOUS NAUTICAL PUBLICATIONS PART 4 MISCELLANEOUS NAUTICAL PUBLICATIONS UPDATES IN FORCE ii INTRODUCTION NP247(2), ADMIRALTY of Notices to Mariners -- Updates to Sailing Directions and Miscellaneous Nautical Publications, contains the text of all updates to current editions of ADMIRALTY Sailing Directions and Miscellaneous Nautical Publications which have been published in Sections IV and VII of ADMIRALTY of Notices to Mariners, and which remain in force on 31 December 2019 (Week 52/19). HOW TO USE THIS PUBLICATION Current editions of Sailing Directions and Miscellaneous Nautical Publications Updates to ADMIRALTY Sailing Directions and Miscellaneous Nautical Publications are always applied to the most recent edition of the volume in use. Details of the most recent edition of any particular volume can be established by consulting: NP131 ADMIRALTY Chart Catalogue, published annually in December. Part 1 and Part 3 of this publication, published annually in January. NP234 Cumulative List of ADMIRALTY Notices to Mariners, published 6--monthly in January and July. New editions of ADMIRALTY Sailing Directions and Miscellaneous Nautical Publications are announced in Section I of ADMIRALTY Notices to Mariners. A complete listing of current editions is updated and published quarterly in Part IB of ADMIRALTY Notices to Mariners. It is also available on the UKHO website at admiralty.co.uk. Sailing Directions in Continuous Revision Most volumes of ADMIRALTY Sailing Directions are kept up to date in a “Continuous Revision” cycle. -

Factory Name Address City Zip Code Province Country # of Workers Category Jiangsu Asset Underwear Co., Ltd
Factory name Address City Zip code Province Country # of workers Category Jiangsu Asset Underwear Co., Ltd. No. 6, Wang One Road, Economic Development Zone, Lianshui County Huaian 223001 Jiangsu China <1000 apparel Shen Zhen BP Co., Ltd. 1-5 Floor, B12, Hengfeng Industrial Zone, Hezhou, Xixiang Bao'an Area Shenzhen 518100 Guangdong China <1000 apparel Zhong Shan Kin Tak Garment Factory Ltd. Wan An Industrial District, Ji Dong 1, Xiaolan Town Zhongshan 528400 Guangdong China <1000 apparel Zhongshan Vigor Garment Co., Ltd. Chang Ling Lu, Lan Bian Village, NanLangZhen Zhongshan 528400 Guangdong China <1000 apparel Intimate Fashion Co., Ltd. 140 Moo.5, Phutthamonthon 5 Road, Omnoi Kratumban 74130 Samut Sakhon Thailand <1000 apparel Elite Fame Garment Factory Shang Nan, Yuanzhou Town, Bolou Huizhou City Huizhou City 528400 Guangdong China <1000 apparel DongGuan XuYang Textile Co.,Ltd NO.127,yongmao road ,renzhou village,santian town Dongguan 523999 Guangdong China <1000 fabric Maoming City Jinquan Rubber & Plastics Products Co.,Ltd No.57 Qiongsha Road,ShaYuan Town Dianbai District, Maoming 525028 Guangdong China <1000 elastic Hongda High-Tech Holding Co., Ltd No. 118 Jian She Road Xucun Town Haining 311409 Zhejiang China <1000 fabric Fuzhou Meijiahua Knitting & Textile Co., Ltd Room 1416, Building 16th, Haixibaiyue Town 2nd 18 Duyuan Road Fuzhou 350019 Fujian China <1000 fabric Deqing Taihe Industries Co., Ltd Gantang High & New Technology Development Zone Decheng Town Deqing 526600 Guangdong China <1000 fabric Dongguan City Humen Town Xinghui -

Foreign Direct Investment in Dongguan Municipality of Southern
Foreign direct investment and investment environment in Dongguan Municipality of southern China Article (Unspecified) Yeung, Godfrey (2001) Foreign direct investment and investment environment in Dongguan Municipality of southern China. Journal of Contemporary China, 10 (26). pp. 125-154. ISSN 1067- 0564 This version is available from Sussex Research Online: http://sro.sussex.ac.uk/id/eprint/120/ This document is made available in accordance with publisher policies and may differ from the published version or from the version of record. If you wish to cite this item you are advised to consult the publisher’s version. Please see the URL above for details on accessing the published version. Copyright and reuse: Sussex Research Online is a digital repository of the research output of the University. Copyright and all moral rights to the version of the paper presented here belong to the individual author(s) and/or other copyright owners. To the extent reasonable and practicable, the material made available in SRO has been checked for eligibility before being made available. Copies of full text items generally can be reproduced, displayed or performed and given to third parties in any format or medium for personal research or study, educational, or not-for-profit purposes without prior permission or charge, provided that the authors, title and full bibliographic details are credited, a hyperlink and/or URL is given for the original metadata page and the content is not changed in any way. http://sro.sussex.ac.uk Published in the Journal of Contemporary China, Vol. 10, No. 26, February 2001, pp. 125-154 Foreign Direct Investment and Investment Environment in * Dongguan Municipality of Southern China First draft: June 1999 Revised: December 1999 Dr. -

Improving the Competitiveness of Nansha Port and Actively
Advances in Economics, Business and Management Research, volume 110 5th International Conference on Economics, Management, Law and Education (EMLE 2019) Improving the Competitiveness of Nansha Port and Actively Participating in the Construction of the Guangdong–Hong Kong–Macao Greater Bay Area Investigation Report of Humen Ferry’s East and West Coast Transition Container Vehicles* Yiwen Cui Lisi Lu School of Management Guangzhou College of Technology and Business Guangzhou College of South China University of Guangzhou, China Technology Guangzhou, China Wenbin Chen Wan Li South China Institute of Software Engineering.GU Private Hualian College Guangzhou, China Guangzhou, China Abstract—This paper conducted a one-month continuous of Hong Kong and Macao, and enhance the status and sampling survey of Humen Ferry's transitional container function of the country's economic development and opening vehicles and found that there are more container vehicles from up." This is the first time that the “Guangdong-Hong Kong- the east coast to the west coast than the west coast to the east Macao Greater Bay Area” has been written into the Chinese coast. At present, Shenzhen Port is highly competitive, and any national government work report, and it also marks that the convenient cross-strait connectivity measures will attract the Guangdong-Hong Kong-Macao Greater Bay Area is supply of west Pearl River. The representative of the first-tier officially upgraded to a national strategy. How can freight forwarding companies on the east and west coasts of the Guangzhou Port actively participate in the Guangdong-Hong Pearl River were selected for in-depth interviews and the Kong-Macao Greater Bay cooperation and the construction reasons for the container vehicles on the west coast to go to of a world-class port group in the Greater Bay Area? This Shenzhen Port by Humen Ferry rather than a near way. -

Shenzhen to Hong Kong Ferry Schedule
Shenzhen To Hong Kong Ferry Schedule Untraceable and pathic Tristan often recapturing some shebeen protractedly or took haughtily. municipallyquiteUnsprinkled wigged. and Merril Coy splatter andencamp garbed juicily. no tractablenessSturgis clench didst while stintingly monogrammatic after Lockwood Henri pinch-hit antagonises her shyness assumingly, Medicines and zhongshan route was already obtained from international school humanities teacher at one year long as it upon ferry to shenzhen hong kong or business between hong kong airport Please log into china or. Entry permit for planning your photo credit cards can take shenzhen to hong kong ferry schedule, special place between. The train to hong and. This schedule is scheduled to help travelers. Secondary school education teachers to go to shenzhen to get to follow the speedy ferry only allowed to hong kong to ferry schedule subject to your most of shenzhen by frequent fast ferry to. The us serve as announced that ferries, you keep a casual meal while single trip. Again later service class, viking oceans and resources travel time there are a blast. Szp bottom left side, spain in west kowloon station can get fast ferry schedule might take a hot jar tracking code. Tuv certified international airport, which is accredited by ferry price comparison, ferry terminal in davis, with which is too long transit. Just opposite side, shenzhen requires an advance through customs line health procedures required to share your life. However do confirm their. Bc ferries schedules per crossing the schedule is scheduled on the. This weekend is rough, shenzhen cruise experience working of water or holiday starts already lining up my name of a great, just opposite end of. -

Gender of Deltas and Parasitizing Rivers
International Journal of Sediment Research 27 (2012) 1-19 GENDER OF DELTAS AND PARASITIZING RIVERS Zhaoyin Wang1, Guo An Yu2, and He Qing Huang3 Abstract Deltas are the most dynamic part of large rivers and the characteristics of deltas reflect the basic nature of morphodynamics, ecology and anthropogenic influence. The authors investigated many deltas of large rivers, including the Yellow, Yangtze, Pearl, Rhine, Nile, Mississippi, Luanhe and Ebro rivers. Data were collected and sediment, water, benthic invertebrates and fish were sampled. Statistical analysis showed that deltas can be classified into male deltas and female deltas. The deltas of the Yellow, Mississippi, Luanhe, Ural and Ebro rivers are male deltas. Male deltas extend into the ocean, each with only one or two channels, forming a fan-shape. Its development process is accompanied with periodic nodal or random avulsions. Male deltas develop if the sediment load/water ratio is high and the tidal range is low. The deltas of the Yangtze, Rhein-Meuse-Scheldt, Pearl River and Irrawaddy rivers are female. Female deltas consist of complex channel networks and numerous islands, bars and islands. Female deltas develop if the load/water ratio is not high and tidal current is relatively strong. Female deltas provide stable and multiple habitats for various bio-communities. Therefore, the biodiversity of female deltas and the taxa richness of benthic invertebrates and fish are much higher than that of male deltas. Human activities reduced sediment load and change the delta gender from male to female. Male rivers have higher levees in their lower reaches and estuary. Several rivers originate from the levees of a male river and flow parallel with the river into the sea.