Optimal Harvesting Decision Paths When Timber and Water Have an Economic Value in Uneven Forests
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Village Montana Randogne Sierre Anzère Aminona Chermig
Le Bâté Donin 2421 m Bella Lui 2543 m Er de Chermignon Chamossaire 2616 m Les Rousses Funitel Plaine Morte Petit Mont Bonvin La Tièche 2383 m 1971 m 1763 m Remointse du Plan Pas de Maimbré 2362 m Cabane des Violees 2209 m Les Taules Plan des Conches Cry d'Er 2109 m Cabane 2263 m de la Tièche Cave de Pra Combère Prabey Merdechon Ravouéné 1617 m Chetseron Alpage 2112 m des Génissons Prabaron Cave du Sex Les Houlés Pépinet Mont Lachaux Hameau Les Bourlas 2140 m de Colombire Violees Grillesse Les Luys L'Aprîli 1711 m Crans-Cry d'ErMerbé La Dent Samarin 1933 m Prodéfure Corbire Plumachit Les Courtavey Marolires 1649 m L'Arbiche L'Arnouva Dougy C Anzère Zironde Aminona La Giète Délé 1514 m 1515 m Les Giees Plans Mayens Lac Pralong 1150 m Chermignon Les Barzees Le Zotset Vermala Chamossaire Montana-Arnouva Zaumiau 1491 m Les Echerts Sion La Fortsey Parking Les Essampilles Crans-Cry d'Er Cordona Lac Ycoor B 1244 m Icogne Crans Lac Grenon La Comba Pra Peluchon Montana Terrain Flouwald football Planige Les Vernasses Etang Long Bluche Randogne Lac Mollens Leuk Moubra A Fortunau Icogne La Délége Grand Zour Saxonne 1046 m St-Romain Lac Etang Briesses Luc Miriouges Arbaz Montana- Village Miège Triona Venthône Leuk Botyre 799 m Villa Darnona Sergnou Chermignon-d'en-Haut Etang La Place du Louché 893 m Salgesch Veyras Lens 1128 m Diogne Loc Muraz Tovachir Chermignon- d'en-Bas 910 m Villa Raspille Liddes Corin-de-la-Crête Flanthey Valençon Sion / Grimisuat Chelin Ollon Sierre St-Clément Noës 533 m Le Rhône Brig / Leuk Pistes VTT / MTB-Strecke VTT / MTB: -

A New Challenge for Spatial Planning: Light Pollution in Switzerland
A New Challenge for Spatial Planning: Light Pollution in Switzerland Dr. Liliana Schönberger Contents Abstract .............................................................................................................................. 3 1 Introduction ............................................................................................................. 4 1.1 Light pollution ............................................................................................................. 4 1.1.1 The origins of artificial light ................................................................................ 4 1.1.2 Can light be “pollution”? ...................................................................................... 4 1.1.3 Impacts of light pollution on nature and human health .................................... 6 1.1.4 The efforts to minimize light pollution ............................................................... 7 1.2 Hypotheses .................................................................................................................. 8 2 Methods ................................................................................................................... 9 2.1 Literature review ......................................................................................................... 9 2.2 Spatial analyses ........................................................................................................ 10 3 Results ....................................................................................................................11 -

Montana-Crans Station Aux Prises Avec Le Morcellement Communal
FONDATION DOCTEUR IGNACE MARIETAN Nous pensons qu'il est utile de faire connaître la fondation instituée par Monsieur Mariétan, et c'est pour cela que nous citons les clauses du testament la concernant. «Je constitue sous le nom «Fondation Dr Ignace Mariétan» une fonda tion au sens des articles 84 et suivants du Code civil et je l'institue mon héritière unique, lui affectant donc tout ce que je possède sous les réserves énoncées ci-après. Le siège de la fondation est à Sion, sa durée est illimitée. Le but de la fondation est: —' de faciliter la préparation, l'exécution, la publication de travaux scientifiques par la Murithienne, ses membres, ses correspondants ou d'autres personnes présentées par elle; —• de contribuer aux frais de l'administration de la Murithienne par des subventions en espèces, l'achat de machines ou d'appareils ou la mise à disposition de ceux-ci; — de couvrir, si besoin, d'autres dépenses de la Murithienne effectuées dans le cadre de son propre but. Le conseil de la fondation, chargé de la gestion de son patrimoine, exa minera les propositions et suggestions présentées par la Murithienne et décidera souverainement de l'utilisation des revenus annuels du patrimoine de la fondation dans les limites du cadre donné par son but. Le conseil de la fondation comprendra trois membres: ... Le monde scientifique et la Murithienne seront toujours représentés dans le conseil de la fondation.» 8 MONTANA-CRANS STATION AUX PRISES AVEC LE MORCELLEMENT COMMUNAL Etude de géographie humaine 1 par Pierrette Jeanneret, Puliy Je tiens tout d'abord à remercier tous ceux qui, par leur collaboration et la gen tillesse avec laquelle ils ont bien voulu répondre à mes questions, m'ont permis de réaliser ce travail. -

Factsheet Crans-Montana 2020
FACTSHEET CRANS-MONTANA 2020 Altitude of Crans-Montana 1’500 meters (resort) to 3’000 m (glacier) 6 villages Icogne, Lens, Chermignon, Montana, Randogne, Mollens 3 municipalities Crans-Montana, Icogne, Lens Surface 97.8 km2 Residents of the 6 villages A bit more than 15’000 people Residents in the resort About 6’000 people Residents/tourists in peak season About 50’000 people 365 days of access to the mountain by ski lifts 9 lakes │ 1 glacier │ 200 hectares of vineyards │ 6 bisses │ 12 historic villages Best of The Alps member since December 2017! Accommodation Among the wide range of high-quality accommodation there is something for every traveller, from five-star hotels and guest houses to mountain huts, a camp site, chalets and apartments for rent. Attentive service by people who are passionate about what they do, together with a warm and friendly atmosphere, make every stay unforgettable. > 30 Hotels - 7 Luxury - 5 First class - 14 Comfort - 5 Economy > 1 Youth Hostel > 13 B&B > 8 Chalets with hotel services > 5 Accommodations for groups > 5 Mountain huts > 1 Camping > 30 Real estate agencies (for apartment / chalet rentals) Gastronomy & Local Produce In Crans-Montana, whether in the resort or on the pistes, when tastebuds quiver every gourmet will find what they’re looking for amongst the huge choice of restaurants which vary from mountain huts to Michelin-starred establishments. 150 Bars and Restaurants Beer/coffee Factory > 6 Clubs > 1 brewery > 2 Michelin starred restaurants > 1 coffee factory where the coffee > 10 Gault & Millau recognition is roasted in the resort restaurants Cheesemaking Wine producers > 24 wine producers in Crans-Montana Visits and tastings on request Chocolatier Lifestyle & Wellbeing Crans-Montana is a place where you can forget your daily stress and live fully in the moment. -
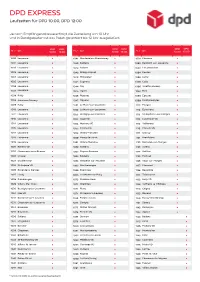
DPD EXPRESS Laufzeiten Für DPD 10:00, DPD 12:00
DPD EXPRESS Laufzeiten für DPD 10:00, DPD 12:00 Je nach Empfängeradresse erfolgt die Zustellung um 10 Uhr und in Randgebieten ist das Paket garantiert bis 12 Uhr ausgeliefert. DPD DPD DPD DPD DPD DPD PLZ Ort 10:00 12:00 PLZ Ort 10:00 12:00 PLZ Ort 10:00 12:00 1000 Lausanne ■ 1041 Montaubion-Chardonney ■ 1091 Chenaux ■ 1001 Lausanne ■ 1042 Bettens ■ 1092 Belmont-sur-Lausanne ■ 1002 Lausanne ■ 1042 Assens ■ 1093 La Conversion ■ 1003 Lausanne ■ 1042 Bioley-Orjulaz ■ 1094 Paudex ■ 1004 Lausanne ■ 1042 Malapalud ■ 1095 Lutry ■ 1005 Lausanne ■ 1043 Sugnens ■ 1096 Cully ■ 1006 Lausanne ■ 1044 Fey ■ 1096 Villette (Lavaux) ■ 1007 Lausanne ■ 1045 Ogens ■ 1097 Riex ■ 1008 Prilly ■ 1046 Rueyres ■ 1098 Epesses ■ 1008 Jouxtens-Mézery ■ 1047 Oppens ■ 1099 Montpreveyres ■ 1009 Pully ■ 1051 Le Mont-sur-Lausanne ■ 1110 Morges ■ 1010 Lausanne ■ 1052 Le Mont-sur-Lausanne ■ 1112 Echichens ■ 1011 Lausanne ■ 1053 Bretigny-sur-Morrens ■ 1113 St-Saphorin-sur-Morges ■ 1012 Lausanne ■ 1053 Cugy VD ■ 1114 Colombier VD ■ 1014 Lausanne ■ 1054 Morrens VD ■ 1115 Vullierens ■ 1015 Lausanne ■ 1055 Froideville ■ 1116 Cottens VD ■ 1017 Lausanne ■ 1058 Villars-Tiercelin ■ 1117 Grancy ■ 1018 Lausanne ■ 1059 Peney-le-Jorat ■ 1121 Bremblens ■ 1019 Lausanne ■ 1061 Villars-Mendraz ■ 1122 Romanel-sur-Morges ■ 1020 Renens VD ■ 1062 Sottens ■ 1123 Aclens ■ 1022 Chavannes-près-Renens ■ 1063 Peyres-Possens ■ 1124 Gollion ■ 1023 Crissier ■ 1063 Boulens ■ 1125 Monnaz ■ 1024 Ecublens VD ■ 1063 Chapelle-sur-Moudon ■ 1126 Vaux-sur-Morges ■ 1025 St-Sulpice VD ■ 1063 Martherenges ■ 1127 -

Dureté De L'eau Dans Le Canton Du Valais
Département de la santé, des affaires sociales et de la culture Service de la consommation et affaires vétérinaires Departement für Gesundheit, Soziales und Kultur Dienststelle für Verbraucherschutz und Veterinärwesen DuretéDépartement desde transports, l’eau de l’équipement et dedans l’environnement le canton du Valais Laboratoire cantonal et affaires vétérinaires Departement für Verkehr, Bau und Umwelt Kantonales Laboratorium und Veterinärwesen CANTON DU VALAIS KANTON WALLIS Rue Pré-d’Amédée 2, 1951 Sion / Rue Pré-d’Amédée 2, 1951 Sitten Tél./Tel. 027 606 49 50 • Télécopie/Fax 027 606 49 54 • e-mail: [email protected] Les communes du Bas-Valais Districts Commune Lieu 0-7 7-15 15-25 25-32 32-42 >42 Districts Commune Lieu 0-7 7-15 15-25 25-32 32-42 >42 Sierre Ayer Nendaz Zinal Bouillet Vétroz Chalais Martigny Bovernier Chandolin Les Nids Chermignon Charrat Chippis Fully Grimentz Isérables Grône Leytron Icogne Martigny Lens Martigny-Combe Miège Riddes Mollens Saillon Montana Saxon Randogne Trient St-Jean Entremont Bagnes St-Léonhard Lourtier/Fregnoley St-Luc Le Chable Sierre Le Cotterg Venthône Bourg-St-Pierre Veyras Liddes Vissoie Le Chable Hérens Les Agettes Orsières Ayent Val Ferret superieur Anzère Rive droite Fortunoz Sembrancher Botyre Vollèges Mayens Pramousse Vollèges (font. église) Evolène St-Maurice Collonges Hérémence Dorénaz Mase Evionnaz Nax Finhaut Marbozet Massongex St-Martin Mex Vernamiège St-Maurice Vex Salvan Ypresse Vernayaz Sion Arbaz Vérossaz Grimisuat Monthey Champéry Salins Collombey-Muraz Savièse Monthey Sion -

Zusammenfassung
Bull. Murithienne 110 (1992): 37-55 CHRONIQUE ORNITHOLOGIQUE VALAISANNE POUR LES ANNEES 1989 ET 1990 par Bertrand Posse1 ZUSAMMENFASSUNG Ornithologische Ergebnisse aus dem Wallis für die Jahre 1989 und 1990 Der Autor sammelt die ornithologischen Beobachtungen aus dem Wallis während der Jahre 1989 und 1990. Neben den Originaldaten von 18 Beobachtern werden auch Ergebnisse, die im «Informationsdienst» der Vogelwarte Sempach oder in der Zeitschrift «Nos Oiseaux» publiziert wurden, aufgeführt. Ce collationnement regroupe les notes de 18 observateurs, complété par des données empruntées à la Station ornithologique de Sempach (S), à la chronique ornithologique romande publiée dans «Nos Oiseaux» (NO) et au fichier Gypaète (G), mis à jour par R. Arlettaz. Quelques modifications ont été apportées à la présentation adoptée en 1979-1980 (Arlettaz & Tenthorey, 1981): les migrations printanière et automnale ont été séparées afin de mieux cerner les différents mouve ments migratoires. Une section particulière a été conservée pour la nidification, en regroupant cette fois-ci tous les indices de présence correspondant aux critères de 1 ' Atlas définis par la Station ornithologique de Sempach. Chaque observation est suivie des initiales de l'auteur ou de son nom complet: RA = Raphaël Arlettaz; DB = Didier Baud; PhB = Philippe Baumann; GC = Gilles Carron; JC = Jesse Curchod; HD = Hubert Duperrex; JF = Jérôme Fournier; CG = Claus Geyer; CK = Christian Keim; AL = Alain Lugon; RL = Ralph Lugon; LM = Lionel Maumary; HM = Hildegard Messerknecht; BP = Bertrand Posse; JCP = Jean-Claude Praz; AS = Antoine Sierro; IS = Irène Simonetta; EW = Emmanuel Widmann. Afin d'éviter des confusions sur les lieux d'observation, toutes les données de la région d'Agarn-Leuk ont été regroupées sous la commune 1 Simplon 11, 1920 Martigny. -

Montana – Mollens – Sierre
Crans-Montana Arts & Métiers Sierre - Crans-Montana FUNICULAIRE ET AUTOBUS Funiculaire Sierre – Montana Lundi - samedi sauf 25,26 déc., 1,2 jan., 19 mars, 5 avril, L’horaire des courses 13, 24 mai, 3 juin, 1,15 août, 1 nov., 8 déc. Brig 100 528 605 628 728 805 828 905 928 1003 1028 1105 1128 1205 1228 1305 1328 1403 1428 1505 1528 1557 1628 1705 1728 1805 1828 1903 1928 2005 2028 omnibus du funiculaire Visp 536 612 636 736 812 836 912 936 1010 1036 1112 1136 1212 1236 1312 1336 1410 1436 1512 1536 1607 1636 1712 1736 1812 1836 1910 1936 2012 2036 J'achète à Crans-Montana Sierre, CFF o 554 635 654 754 835 854 935 954 1033 1054 1135 1154 1235 1254 1335 1354 1433 1454 1535 1554 1625 1654 1735 1754 1835 1854 1933 1954 2035 2054 peut varier en fonction du † Dimanches et 25,26 déc., 1,2 jan., 19 mars, 5 avril, au même prix qu'en plaine! Lausanne 100 545 645 720 745 824 845 920 945 1020 1045 1120 1145 1220 1245 1320 1345 1424 1445 1520 1545 1620 1645 1720 1745 1820 1845 1920 1945 nombre d’arrêts sollicités 13, 24 mai, 3 juin, 1,15 août, 1 nov., 8 déc. Sion 624 654 754 824 854 928 954 1024 1054 1124 1154 1224 1254 1324 1354 1424 1454 1528 1554 1624 1654 1724 1754 1824 1854 1924 1954 2028 2054 Sierre, CFF o 633 703 803 833 903 937 1003 1033 1103 1133 1203 1233 1303 1333 1403 1433 1503 1537 1603 1633 1703 1733 1803 1833 1903 1933 2003 2037 2103 (arrêt sur demande) 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 a Durant les périodes scolaires Sierre / Siders 20 625 650 725 815 845 915 945 1015 1045 1115 -

JDS-2012-04-13.Pdf
DISTRIBUTION TOUS MÉNAGES A. ANTILLE SIERRE SA AGENCES Av. Général-Guisan 5 - 027 455 12 72 BIMENSUEL | JGA 3960 Sierre Vendredi 13 avril 2012 | No 7 | 98e année Le retour de Céline MONTANA | Céline Rey appartient à la Compa- gnie Broadway. La troupe professionnelle de comé- diemusicaleseproduira à Montana-Village les 27 et 28 avril. Un retour aux sources pour l’artiste montanaise. Portrait. >27 Le Romandie avec Tschopp CYCLISME | Le chrono prévu à Crans-Montana le 29 avril va être le juge de paix du Tour de Romandie. Cerise sur le gâteau: Johann Tschopp Les REINES sera au départ de cette épreuve, avant son ren- dez-vous avec le Giro. s’impatientents’impatientent >31 Temps d’arrêt 2 MOLLENS | Le plateau de Conzor s’apprête L’info 6 à accueillir un combat de reines les 21 et 22 avril. Gens d’ici 11 La Noble-Contrée est mobilisée. ARCHIVES REMO Culture-Société 24 > 4-5 Sports 31 PUB On cherche terrains <wm>%"0g1+bnI%K6%4gh8%7S%tV'=z-hZ2dzn-lT-/jkRlOy82%U3%9nDp%Sy</wm> <wm>%"0g1+bnI%K6%4gh8%7S%tV'=z-hZ2dzL-lT-/jkRlOy8l%U3%9nDp%Sy</wm> LAURENT BRANDI <wm>%"0g1+bnI%K6%4gh8%7S%tV'=z-hZYoWe-lT-/jkRlOy8l%U3%9nDp%Sy</wm> <wm>%4qwB+hgm%j/%EwPl%Ca+ANDJX%3x%c4=.C%7S+=HzEj%vT%N"e.7%LB+Z6ckcQD%UL%9tJ32wyQ%0d%O5HYF-AJX2s/-Cv-jDxwCahQC%Gg%l'p4%dh%DlL/ub%XmO'o-LRHuPl-rb-CqyKrIE/r.YGQ%ow%'1fRm2%ra%/2r1nmSbfZb%0TUtV.fLh%Q"%yPQgvGrdbmd%7q%R57YeaLEfW2r%ovGu5.dtG%re%h6r1nmwRL"bX%dh%DlU/1b%Xm5Rq+g3W+Nd+BD%iKnk%lIJ=+vu2+X1G'%3a%cdFOog%5e</wm> <wm>%gyDp+7z8%kH%wDlO%aZ+0"xrW%K6%4g1.a%Si+15Twk%Ah%"n'.S%Bp+QC4P4Xx%cB%tGrKfDJX%dE%m95Nv-0rtLvV-aA-kx6DaZ7Xt%uz%OV3g%E7%xOBH=L%W8mVb-BjYgbG-IL-ayJqIswHY.NuX%bD%VFUj8f%IZ%HfIFM8iLUQL%dhcGp.LUp%Xn%JlXzAuIEL8E%Sy%j9SN'ZBwUefI%bAu=3.q"Q%I'%7CIFM8DjBnLW%E7%xOcHFL%W89jy+NU7+"L+o3%Rq04%OsxK+A=4U+ev=2%qQ%gwA8LT%tV</wm> -

Survol Dessecours Valaisans
GENS D’ICI SORTIR A. ANTILLE SIERRE SA FLANTHEY MOLLENS AGENCES LA MEILLEURE LES CONTEUSES ANNE SYRAHDUVALAIS MARTIN ET CHRISTINE EST L’ŒUVRE DE MÉTRAILLER TIRENT L’ENCAVEUR 6 LEUR RÉVÉRENCE. 31 CHRISTIAN LAMON. LEJOURNAL BIMENSUEL DE SIERRE JGA 3960 SIERRE DISTRIBUTION TOUS MÉNAGES Vendredi No 22 6 décembre 2013 ACTU Survol ANNIVIERS La commune inau- gure une piscine à des secours Zinal. Pleins feux sur les infrastructures anniviardes. >4 valaisans SPORTS VENTHÔNE L’année de Yann Martiaétéexcep- tionnelle: 599 places gagnées à l’ATP. >27 SIERRE Jean-Marc Bellagamba dirige l’OCVS (Organisation cantonale valaisanne des secours) depuis une année. Il Av. Général-Guisan 5 - 027 455 12 72 dresse le bilan de son action, à l’aube de la saison hivernale. HOFMANN/NF > 16-17 WWW.LEJDS.CH [email protected] PUB On cherche terrains Hyundai <wm>10CAsNsjY0MDA20zWzNLUwswAAC-L4Sw8AAAA=</wm> LAURENT BRANDI<wm>10CAsNsjY0MDA20zWzNLUwNwUA969SLA8AAAA=</wm> <wm>10CAsNsjY0MDA20zU3NDI1MwMAgvxjwg8AAAA=</wm><wm>10CAsNsjY0MDA20zU3NDI1MwYADQgJsg8AAAA=</wm><wm>10CAsNsjY0MDA20zU3NDI1MwIAmzgOxQ8AAAA=</wm> ix35 <wm>10CFWMMQrDQAwEX6RjV9IJOVcadyZFcK_GpM7_q5zduViGgWH3ffSGe-v2PrbPIGAhsfSMHExv2nWQ1ixjUlVBe2GBMs0fuVhMA-pKBCrwQgogtKKiaPOARTcH2-_8_gGLKpDzfwAAAA==</wm> Agent<wm>10CFWMMQ6EMAwEX-Ro145NICWiQ1ec6N0gav5fXY6OYjUaabT73r3g2bp9ju3bCVhIzN4m72y1qGsnrViLQVUFbWH1Rs4ar14shgH5bwQUTMkQN1GmU5M2HpisVsFyn9cP_aL1sIAAAAA=</wm> officiel <wm>10CFXKrQ6AMAxF4Sfqcm9Ly88kmVsQBD9D0Ly_YuAQR5zkqzV7wtda<wm>10CFWMoQ7DMBBDv-gi29dckwVOZVXBNH6kKt7_ozV<wm>10CFWMrQ6AMBCDn-iW63V_MElwBEHwMwTN-ytuOETTNv3jAwZPfva-j1rwy3M73ttrEPCwlarhg20pqhqkF29xl-oC_cSbWsp6Kdl3c_1aFBllgJL2RpqDJbcwcCafTQztqPsmYCFjFSPyJyGpK6ZtGRTf4UpaAs7os6OnxeLfkB7jBWeQRadI_nhh9qbaByNQMesemATscYKX8eA2wPBc9FAl7y2P988bgJyOkaYejIMzbBkX5X0-ZBzDVAF1ggxFx_aOGu6z-sBxmh3gZTPeX0BsnKohYAAAAA=</wm>HIAAAA=</wm>ws-FnpbgAAAAA==</wm> -

Conference Presentation Reference
Conference Presentation In the search of explaining Local Regulatory Arrangements in Crans-Montana BRETHAUT, Christian Reference BRETHAUT, Christian. In the search of explaining Local Regulatory Arrangements in Crans-Montana. In: POLIRSURD Workshop, Crêt-Bêrard, Switzerland, 10-11 février, 2015 Available at: http://archive-ouverte.unige.ch/unige:74457 Disclaimer: layout of this document may differ from the published version. 1 / 1 In the search of explaining Local Regulatory Arrangements in Crans- Montana POLIRSURD Workshop 10-11.2.2015, Crêt-Bêrard Christian Bréthaut, Geneva Water Hub Institute for environmental sciences University of Geneva [email protected] Outline of the presentation - Water and tourism - Crans-Montana: context - The Local Regulatory Arrangement (LRA) - The LRA in Crans-Montana - A reading of this case through the lens of NIE Water and tourism (1) - Tourism implies an unusual water consumption - Peaks of consumption - Great fluctuation of inhabitants of the tourism resort - In consequence, in the field: - Necessity to calibrate infrastructures following the highest number of users - Difficulties in planning the needs - Strong and punctual intersectoral rivalries Water and tourism (2) An interesting context to study: - How do stakeholders interact? - What is the functioning of institutions? - What makes the system work on the long term? The case of Crans-Montana 85 │ - One ski resort in the Swiss N Glacier de la Plaine Morte Alps divided between six La Tièche municipalities La Raspille L’Ertentse - Crossed-interdependencies -

Des Origines D'une Région Autarcique Au Développement D'une Ville
Des origines d’une région autarcique au développement d’une ville touristique à la montagne Table des matières.................................................................................................................. Introduction: une région faite pour le tourisme........................................................................2 Les origines de l’autonomie des villages ................................................................................3 Les guerres: une occasion de découvrir le monde..................................................................3 La tension monte entre les collectivités réunies de force........................................................4 L’apprentissage de l’hôtellerie à l’étranger..............................................................................4 1890: construction du premier hôtel........................................................................................5 Le ski, dès 1905 .....................................................................................................................6 De neige et de glace ..............................................................................................................6 Le charme des randonnées estivales .....................................................................................7 Le ski en hiver, le golf en été..................................................................................................7 D’autres loisirs se développent...............................................................................................8