DOCSLIB.ORG

Chapter 31 Ideal Gas Laws

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 31 Ideal Gas Laws CHAPTER 31 IDEAL GAS LAWS EXERCISE 144, Page 317 1. The pressure of a mass of gas is increased from 150 kPa to 750 kPa at constant temperature. Determine the final volume of the gas, if its initial volume is 1.5 m 3 . Since the change occurs at constant temperature (i.e. an isothermal change), Boyle's law applies, 3 i.e. p 1 V 1 = p 2 V 2 where p 1 = 150 kPa, p 2 = 750 kPa and V 1 = 1.5 m Hence, (150)(1.5) = (750)V 2 150 1.5 from which, volume V = = 0.3 m 3 2 750 2. In an isothermal process, a mass of gas has its volume reduced from 50 cm 3 to 32 cm 3 . If the initial pressure of the gas is 80 kPa, determine its final pressure. Since the change occurs at constant temperature (i.e. an isothermal change), Boyle's law applies, 3 3 i.e. p 1 V 1 = p 2 V 2 where p 1 = 80 kPa, V 1 = 50 cm and V 2 = 32 cm Hence, (80)(50) = (p 2 )(32) 80 50 from which, pressure p = = 125 kPa 2 32 1 3. The piston of an air compressor compresses air to of its original volume during its stroke. 4 Determine the final pressure of the air if the original pressure is 100 kPa, assuming an isothermal change. Since the change occurs at constant temperature (i.e. an isothermal change), Boyle's law applies, 354 © John Bird Published by Taylor and Francis 1 i.e. p V = p V where p = 100 kPa, V = V 1 1 2 2 1 2 4 1 1 Hence, (100)( V ) = (p )( V ) 1 2 4 1 100 V 100 from which, pressure p = 1 = 400 kPa 2 11 V 441 4. A quantity of gas in a cylinder occupies a volume of 2 m 3 at a pressure of 300 kPa. A piston slides in the cylinder and compresses the gas, according to Boyle's law, until the volume is 0.5 m 3 . If the area of the piston is 0.02 m 2 , calculate the force on the piston when the gas is compressed. An isothermal process means constant temperature and thus Boyle's law applies, i.e. p 1 V 1 = p 2 V 2 3 3 where V 1 = 2 m , V 2 = 0.5 m and p 1 = 300 kPa. Hence, (300)(2) = p 2 (0.5) 300 2 from which, pressure, p = = 1200 kPa 2 0.5 force Pressure = , from which, force = pressure area. area Hence, force on the piston = (1200 10 3 Pa)(0.02 m 2 ) = 24000 N = 24 kN 5. The gas in a simple pump has a pressure of 400 mm of mercury (Hg) and a volume of 10 mL. If the pump is compressed to a volume of 2 mL, calculate the pressure of the gas, assuming that its temperature does not change? Since PV11 PV 2 2 then (400 mm Hg)(10 mL) = ( P2 )(2 mL) 355 © John Bird Published by Taylor and Francis 400mm Hg 10mL from which, new pressure, P = = 2000 mm of mercury 2 2mL 356 © John Bird Published by Taylor and Francis EXERCISE 145, Page 319 1. Some gas initially at 16C is heated to 96C at constant pressure. If the initial volume of the gas is 0.8 m 3 , determine the final volume of the gas. Since the change occurs at constant pressure (i.e. an isobaric process), Charles’ law applies, VV i.e. 12 TT12 3 where V 1 = 0.8 m , T 1 = 16C = (16 + 273)K = 289 K and T 2 = (96 + 273)K = 369 K. 0.8 V Hence, 2 289 369 (0.8)(369) from which, volume at 96C, V = = 1.02 m 3 2 289 2. A gas is contained in a vessel of volume 0.02 m 3 at a pressure of 300 kPa and a temperature of 15C. The gas is passed into a vessel of volume 0.015 m 3 . Determine to what temperature the gas must be cooled for the pressure to remain the same. Since the process is isobaric it takes place at constant pressure and hence Charles’ law applies, VV i.e. 12 TT12 3 3 where T 1 = (15 + 273)K = 288 K and V 1 = 0.02 m and V 2 = 0.015 m 0.02 0.015 Hence 288 T2 (0.015)(288) from which, final temperature, T = = 216 K or (216 - 273)C i.e. - 57C 2 0.02 3. In an isobaric process gas at a temperature of 120C has its volume reduced by a sixth. Determine the final temperature of the gas. Since the process is isobaric it takes place at constant pressure and hence Charles’ law applies, 357 © John Bird Published by Taylor and Francis VV i.e. 12 TT12 5 where T = (120 + 273)K = 393 K and V = V 1 2 6 1 5 V V 1 Hence 1 6 393 T2 5 V1 393 6 5 from which, final temperature, T 2 = 393 = 327.5 K V61 = (327.5 - 273)C = 54.5C 4. The volume of a balloon is 30 litres at a temperature of 27ºC. If the balloon is under a constant internal pressure, calculate its volume at a temperature of 12ºC. VV Since 12 TT12 where T1 = (27 + 273)K = 300 K and T2 = (12 + 273)K = 285 K 30litres V Hence, 2 300K 285K 30litres 285K and new volume, V = = 28.5 litres 2 300K 358 © John Bird Published by Taylor and Francis EXERCISE 146, Page 320 1. Gas, initially at a temperature of 27C and pressure 100 kPa, is heated at constant volume until its temperature is 150C. Assuming no loss of gas, determine the final pressure of the gas. pp Since the gas is at constant volume, the pressure law applies, i.e. 12 TT12 where T 1 = (27 + 273)K = 300 K, T 2 = (150 + 273)K = 423 K and p 1 = 100 kPa 100 p Hence, 2 300 423 (100)(423) from which, final pressure, p = = 141 kPa 2 300 2. A pressure vessel is subjected to a gas pressure of 8 atmospheres at a temperature of 15ºC. The vessel can withstand a maximum pressure of 28 atmospheres. Calculate the gas temperature increase the vessel can withstand. PP Since 12 TT12 where T1 = (15 + 273)K = 288 K 8atmospheres 28atmospheres Hence, 288K T2 28atmospheres 288K from which, new temperature, T = = 1008 K or (1008 – 273)ºC = 735ºC 2 8atmospheres Hence, temperature rise = (1008 – 288)K = 720 K or temperature rise = (735 – 15)ºC = 720ºC Note that a temperature change of 720 K = a temperature change of 720ºC 359 © John Bird Published by Taylor and Francis EXERCISE 147, Page 321 1. A gas A in a container exerts a pressure of 120 kPa at a temperature of 20C. Gas B is added to the container and the pressure increases to 300 kPa at the same temperature. Determine the pressure that gas B alone exerts at the same temperature. Initial pressure, p A = 120 kPa, and the pressure of gases A and B together, p = p A + p B = 300 kPa By Dalton's law of partial pressure, the pressure of gas B alone is p B = p - p A = 300 - 120 = 180 kPa 360 © John Bird Published by Taylor and Francis EXERCISE 148, Page 322 1. A gas occupies a volume of 1.20 m 3 when at a pressure of 120 kPa and a temperature of 90C. Determine the volume of the gas at 20C if the pressure is increased to 320 kPa. pV pV Using the combined gas law: 11 2 2 TT12 3 where V 1 = 1.20 m , p 1 = 120 kPa, p 2 = 320 kPa, T 1 = (90 + 273)K = 363 K and (120)(1.20) (320) V T = (20 + 273)K = 293 K, gives: 2 2 363 293 (120)(1.20)(293) from which, volume at 20C, V = = 0.363 m 3 2 (363)(320) 2. A given mass of air occupies a volume of 0.5 m 3 at a pressure of 500 kPa and a temperature of 20C. Find the volume of the air at STP. pV pV Using the combined gas law: 11 2 2 TT12 3 where V 1 = 0.5 m , p 1 = 500 kPa, T 1 = (20 + 273)K = 293 K , p 2 = 101.325 kPa, and (500)(0.5) (101.325) V T = 0C = 273 K, gives: 2 2 293 273 (500)(0.5)(273) from which, volume at STP, V = = 2.30 m 3 2 (293)(101.325) 3. A balloon is under an internal pressure of 110 kPa with a volume of 16 litres at a temperature of 22ºC. If the balloon’s internal pressure decreases to 50 kPa, what will be its volume if the temperature also decreases to 12ºC. 361 © John Bird Published by Taylor and Francis pV pV Using the combined gas law: 11 2 2 TT12 where V 1 = 16 litres, p 1 = 110 kPa, p 2 = 50 kPa, T 1 = (22 + 273)K = 295 K and (110)(16) (50) V T = (12 + 273)K = 285 K, gives: 2 2 295 285 (110)(16)(285) from which, volume at 12C, V = = 34.0 litres 2 (295)(50) 4. A spherical vessel has a diameter of 2.0 m and contains hydrogen at a pressure of 300 kPa and a temperature of - 30C. Determine the mass of hydrogen in the vessel.
Load more

Recommended publications
  • Thermodynamics Notes
    Thermodynamics Notes Steven K. Krueger Department of Atmospheric Sciences, University of Utah August 2020 Contents 1 Introduction 1 1.1 What is thermodynamics? . .1 1.2 The atmosphere . .1 2 The Equation of State 1 2.1 State variables . .1 2.2 Charles' Law and absolute temperature . .2 2.3 Boyle's Law . .3 2.4 Equation of state of an ideal gas . .3 2.5 Mixtures of gases . .4 2.6 Ideal gas law: molecular viewpoint . .6 3 Conservation of Energy 8 3.1 Conservation of energy in mechanics . .8 3.2 Conservation of energy: A system of point masses . .8 3.3 Kinetic energy exchange in molecular collisions . .9 3.4 Working and Heating . .9 4 The Principles of Thermodynamics 11 4.1 Conservation of energy and the first law of thermodynamics . 11 4.1.1 Conservation of energy . 11 4.1.2 The first law of thermodynamics . 11 4.1.3 Work . 12 4.1.4 Energy transferred by heating . 13 4.2 Quantity of energy transferred by heating . 14 4.3 The first law of thermodynamics for an ideal gas . 15 4.4 Applications of the first law . 16 4.4.1 Isothermal process . 16 4.4.2 Isobaric process . 17 4.4.3 Isosteric process . 18 4.5 Adiabatic processes . 18 5 The Thermodynamics of Water Vapor and Moist Air 21 5.1 Thermal properties of water substance . 21 5.2 Equation of state of moist air . 21 5.3 Mixing ratio . 22 5.4 Moisture variables . 22 5.5 Changes of phase and latent heats .
    [Show full text]
  • Chapter 3. Second and Third Law of Thermodynamics
    Chapter 3. Second and third law of thermodynamics Important Concepts Review Entropy; Gibbs Free Energy • Entropy (S) – definitions Law of Corresponding States (ch 1 notes) • Entropy changes in reversible and Reduced pressure, temperatures, volumes irreversible processes • Entropy of mixing of ideal gases • 2nd law of thermodynamics • 3rd law of thermodynamics Math • Free energy Numerical integration by computer • Maxwell relations (Trapezoidal integration • Dependence of free energy on P, V, T https://en.wikipedia.org/wiki/Trapezoidal_rule) • Thermodynamic functions of mixtures Properties of partial differential equations • Partial molar quantities and chemical Rules for inequalities potential Major Concept Review • Adiabats vs. isotherms p1V1 p2V2 • Sign convention for work and heat w done on c=C /R vm system, q supplied to system : + p1V1 p2V2 =Cp/CV w done by system, q removed from system : c c V1T1 V2T2 - • Joule-Thomson expansion (DH=0); • State variables depend on final & initial state; not Joule-Thomson coefficient, inversion path. temperature • Reversible change occurs in series of equilibrium V states T TT V P p • Adiabatic q = 0; Isothermal DT = 0 H CP • Equations of state for enthalpy, H and internal • Formation reaction; enthalpies of energy, U reaction, Hess’s Law; other changes D rxn H iD f Hi i T D rxn H Drxn Href DrxnCpdT Tref • Calorimetry Spontaneous and Nonspontaneous Changes First Law: when one form of energy is converted to another, the total energy in universe is conserved. • Does not give any other restriction on a process • But many processes have a natural direction Examples • gas expands into a vacuum; not the reverse • can burn paper; can't unburn paper • heat never flows spontaneously from cold to hot These changes are called nonspontaneous changes.
    [Show full text]
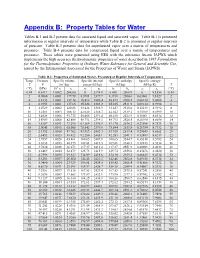
  • Appendix B: Property Tables for Water
    Appendix B: Property Tables for Water Tables B-1 and B-2 present data for saturated liquid and saturated vapor. Table B-1 is presented information at regular intervals of temperature while Table B-2 is presented at regular intervals of pressure. Table B-3 presents data for superheated vapor over a matrix of temperatures and pressures. Table B-4 presents data for compressed liquid over a matrix of temperatures and pressures. These tables were generated using EES with the substance Steam_IAPWS which implements the high accuracy thermodynamic properties of water described in 1995 Formulation for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, issued by the International Associated for the Properties of Water and Steam (IAPWS). Table B-1: Properties of Saturated Water, Presented at Regular Intervals of Temperature Temp. Pressure Specific volume Specific internal Specific enthalpy Specific entropy T P (m3/kg) energy (kJ/kg) (kJ/kg) (kJ/kg-K) T 3 (°C) (kPa) 10 vf vg uf ug hf hg sf sg (°C) 0.01 0.6117 1.0002 206.00 0 2374.9 0.000 2500.9 0 9.1556 0.01 2 0.7060 1.0001 179.78 8.3911 2377.7 8.3918 2504.6 0.03061 9.1027 2 4 0.8135 1.0001 157.14 16.812 2380.4 16.813 2508.2 0.06110 9.0506 4 6 0.9353 1.0001 137.65 25.224 2383.2 25.225 2511.9 0.09134 8.9994 6 8 1.0729 1.0002 120.85 33.626 2385.9 33.627 2515.6 0.12133 8.9492 8 10 1.2281 1.0003 106.32 42.020 2388.7 42.022 2519.2 0.15109 8.8999 10 12 1.4028 1.0006 93.732 50.408 2391.4 50.410 2522.9 0.18061 8.8514 12 14 1.5989 1.0008 82.804 58.791 2394.1 58.793 2526.5
    [Show full text]
  • Equation of State of an Ideal Gas
    ASME231 Atmospheric Thermodynamics NC A&T State U Department of Physics Dr. Yuh-Lang Lin http://mesolab.org [email protected] Lecture 3: Equation of State of an Ideal Gas As mentioned earlier, the state of a system is the condition of the system (or part of the system) at an instant of time measured by its properties. Those properties are called state variables, such as T, p, and V. The equation which relates T, p, and V is called equation of state. Since they are related by the equation of state, only two of them are independent. Thus, all the other thermodynamic properties will depend on the state defined by two independent variables by state functions. PVT system: The simplest thermodynamic system consists of a fixed mass of a fluid uninfluenced by chemical reactions or external fields. Such a system can be described by the pressure, volume and temperature, which are related by an equation of state f (p, V, T) = 0, (2.1) 1 where only two of them are independent. From physical experiments, the equation of state for an ideal gas, which is defined as a hypothetical gas whose molecules occupy negligible space and have no interactions, may be written as p = RT, (2.2) or p = RT, (2.3) where -3 : density (=m/V) in kg m , 3 -1 : specific volume (=V/m=1/) in m kg . R: specific gas constant (R=R*/M), -1 -1 -1 -1 [R=287 J kg K for dry air (Rd), 461 J kg K for water vapor for water vapor (Rv)].
    [Show full text]
  • [5] Magnetic Densimetry: Partial Specific Volume and Other Applications
    74 MOLECULAR WEIGHT DETERMINATIONS [5] [5] Magnetic Densimetry: Partial Specific Volume and Other Applications By D. W. KUPKE and J. W. BEAMS This chapter consists of three parts. Part I is a summary of the principles and current development of the magnetic densimeter, with which density values may be obtained conveniently on small volumes of solution with the speed and accuracy required for present-day ap- plications in protein chemistry. In Part II, the applications, including definitions, are outlined whereby the density property may be utilized for the study of protein solutions. Finally, in Part III, some practical aspects on the routine determination of densities of protein solutions by magnetic densimetry are listed. Part I. Magnetic Densimeter The magnetic densimeter measures by electromagnetic methods the vertical (up or down) force on a totally immersed buoy. From these measured forces together with the known mass and volume of the buoy, the density of the solution can be obtained by employing Archimedes' principle. In practice, it is convenient to eliminate evaluation of the mass and volume of the buoy and to determine the relation of the mag- netic to the mechanical forces on the buoy by direct calibration of the latter when it is immersed in liquids of known density. Several workers have devised magnetic float methods for determin- ing densities, but the method first described by Lamb and Lee I and later improved by MacInnes, Dayhoff, and Ray: is perhaps the most accurate means (~1 part in 106) devised up to that time for determining the densities of solutions. The magnetic method was not widely used, first because it was tedious and required considerable manipulative skill; second, the buoy or float was never stationary for periods long enough to allow ruling out of wall effects, viscosity perturbations, etc.; third, the technique required comparatively large volumes of the solution (350 ml) for accurate measurements.
    [Show full text]
  • Chapter 3 3.4-2 the Compressibility Factor Equation of State
    Chapter 3 3.4-2 The Compressibility Factor Equation of State The dimensionless compressibility factor, Z, for a gaseous species is defined as the ratio pv Z = (3.4-1) RT If the gas behaves ideally Z = 1. The extent to which Z differs from 1 is a measure of the extent to which the gas is behaving nonideally. The compressibility can be determined from experimental data where Z is plotted versus a dimensionless reduced pressure pR and reduced temperature TR, defined as pR = p/pc and TR = T/Tc In these expressions, pc and Tc denote the critical pressure and temperature, respectively. A generalized compressibility chart of the form Z = f(pR, TR) is shown in Figure 3.4-1 for 10 different gases. The solid lines represent the best curves fitted to the data. Figure 3.4-1 Generalized compressibility chart for various gases10. It can be seen from Figure 3.4-1 that the value of Z tends to unity for all temperatures as pressure approach zero and Z also approaches unity for all pressure at very high temperature. If the p, v, and T data are available in table format or computer software then you should not use the generalized compressibility chart to evaluate p, v, and T since using Z is just another approximation to the real data. 10 Moran, M. J. and Shapiro H. N., Fundamentals of Engineering Thermodynamics, Wiley, 2008, pg. 112 3-19 Example 3.4-2 ---------------------------------------------------------------------------------- A closed, rigid tank filled with water vapor, initially at 20 MPa, 520oC, is cooled until its temperature reaches 400oC.
    [Show full text]
  • Ideal Gasses Is Known As the Ideal Gas Law
    ESCI 341 – Atmospheric Thermodynamics Lesson 4 –Ideal Gases References: An Introduction to Atmospheric Thermodynamics, Tsonis Introduction to Theoretical Meteorology, Hess Physical Chemistry (4th edition), Levine Thermodynamics and an Introduction to Thermostatistics, Callen IDEAL GASES An ideal gas is a gas with the following properties: There are no intermolecular forces, except during collisions. All collisions are elastic. The individual gas molecules have no volume (they behave like point masses). The equation of state for ideal gasses is known as the ideal gas law. The ideal gas law was discovered empirically, but can also be derived theoretically. The form we are most familiar with, pV nRT . Ideal Gas Law (1) R has a value of 8.3145 J-mol1-K1, and n is the number of moles (not molecules). A true ideal gas would be monatomic, meaning each molecule is comprised of a single atom. Real gasses in the atmosphere, such as O2 and N2, are diatomic, and some gasses such as CO2 and O3 are triatomic. Real atmospheric gasses have rotational and vibrational kinetic energy, in addition to translational kinetic energy. Even though the gasses that make up the atmosphere aren’t monatomic, they still closely obey the ideal gas law at the pressures and temperatures encountered in the atmosphere, so we can still use the ideal gas law. FORM OF IDEAL GAS LAW MOST USED BY METEOROLOGISTS In meteorology we use a modified form of the ideal gas law. We first divide (1) by volume to get n p RT . V we then multiply the RHS top and bottom by the molecular weight of the gas, M, to get Mn R p T .
    [Show full text]
  • TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # M3/Kg Kj/Kg Kj/Kg Kj/Kg K Sat
    720 Tables in SI Units TABLE A-2 Properties of Saturated Water (Liquid–Vapor): Temperature Table Specific Volume Internal Energy Enthalpy Entropy # m3/kg kJ/kg kJ/kg kJ/kg K Sat. Sat. Sat. Sat. Sat. Sat. Sat. Sat. Temp. Press. Liquid Vapor Liquid Vapor Liquid Evap. Vapor Liquid Vapor Temp. Њ v ϫ 3 v Њ C bar f 10 g uf ug hf hfg hg sf sg C O 2 .01 0.00611 1.0002 206.136 0.00 2375.3 0.01 2501.3 2501.4 0.0000 9.1562 .01 H 4 0.00813 1.0001 157.232 16.77 2380.9 16.78 2491.9 2508.7 0.0610 9.0514 4 5 0.00872 1.0001 147.120 20.97 2382.3 20.98 2489.6 2510.6 0.0761 9.0257 5 6 0.00935 1.0001 137.734 25.19 2383.6 25.20 2487.2 2512.4 0.0912 9.0003 6 8 0.01072 1.0002 120.917 33.59 2386.4 33.60 2482.5 2516.1 0.1212 8.9501 8 10 0.01228 1.0004 106.379 42.00 2389.2 42.01 2477.7 2519.8 0.1510 8.9008 10 11 0.01312 1.0004 99.857 46.20 2390.5 46.20 2475.4 2521.6 0.1658 8.8765 11 12 0.01402 1.0005 93.784 50.41 2391.9 50.41 2473.0 2523.4 0.1806 8.8524 12 13 0.01497 1.0007 88.124 54.60 2393.3 54.60 2470.7 2525.3 0.1953 8.8285 13 14 0.01598 1.0008 82.848 58.79 2394.7 58.80 2468.3 2527.1 0.2099 8.8048 14 15 0.01705 1.0009 77.926 62.99 2396.1 62.99 2465.9 2528.9 0.2245 8.7814 15 16 0.01818 1.0011 73.333 67.18 2397.4 67.19 2463.6 2530.8 0.2390 8.7582 16 17 0.01938 1.0012 69.044 71.38 2398.8 71.38 2461.2 2532.6 0.2535 8.7351 17 18 0.02064 1.0014 65.038 75.57 2400.2 75.58 2458.8 2534.4 0.2679 8.7123 18 19 0.02198 1.0016 61.293 79.76 2401.6 79.77 2456.5 2536.2 0.2823 8.6897 19 20 0.02339 1.0018 57.791 83.95 2402.9 83.96 2454.1 2538.1 0.2966 8.6672 20 21 0.02487 1.0020
    [Show full text]
  • Estimation of Internal Pressure of Liquids and Liquid Mixtures
    Available online at www.ilcpa.pl International Letters of Chemistry, Physics and Astronomy 5 (2012) 1-7 ISSN 2299-3843 Estimation of internal pressure of liquids and liquid mixtures N. Santhi 1, P. Sabarathinam 2, G. Alamelumangai 1, J. Madhumitha 1, M. Emayavaramban 1 1Department of Chemistry, Government Arts College, C.Mutlur, Chidambaram-608102, India 2Retd. Registrar & Head of the Department of Technology, Annamalai University, Annamalainagar-608002, India E-mail address: [email protected] ABSTRACT By combining the van der Waals’ equation of state and the Free Length Theory of Jacobson, a new theoretical model is developed for the prediction of internal pressure of pure liquids and liquid mixtures. It requires only the molar volume data in addition to the ratio of heat capacities and critical temperature. The proposed model is simple, reliably accurate and capable of predicting internal pressure of pure liquids with an average absolute deviation of 4.24% in the predicted internal pressure values compared to those given in literature. The average absolute deviation in the predicted internal pressure values through the proposed model for the five binary liquid mixtures tested varies from 0.29% to 1.9% when compared to those of literature values. Keywords: van der Waals, pressure of liquids, theory of Jacobson, capacity of heat liquids, equation of Srivastava and Berkowitz 1. INTRODUTION The importance of internal pressure in understanding the properties of liquids and the full potential of internal pressure as a structural probe did become apparent with the pioneering work of Hildebrand 1, 2 and the first review of the subject by Richards 3 appeared in 1925.
    [Show full text]
  • The Carnot Cycle, Reversibility and Entropy
    entropy Article The Carnot Cycle, Reversibility and Entropy David Sands Department of Physics and Mathematics, University of Hull, Hull HU6 7RX, UK; [email protected] Abstract: The Carnot cycle and the attendant notions of reversibility and entropy are examined. It is shown how the modern view of these concepts still corresponds to the ideas Clausius laid down in the nineteenth century. As such, they reflect the outmoded idea, current at the time, that heat is motion. It is shown how this view of heat led Clausius to develop the entropy of a body based on the work that could be performed in a reversible process rather than the work that is actually performed in an irreversible process. In consequence, Clausius built into entropy a conflict with energy conservation, which is concerned with actual changes in energy. In this paper, reversibility and irreversibility are investigated by means of a macroscopic formulation of internal mechanisms of damping based on rate equations for the distribution of energy within a gas. It is shown that work processes involving a step change in external pressure, however small, are intrinsically irreversible. However, under idealised conditions of zero damping the gas inside a piston expands and traces out a trajectory through the space of equilibrium states. Therefore, the entropy change due to heat flow from the reservoir matches the entropy change of the equilibrium states. This trajectory can be traced out in reverse as the piston reverses direction, but if the external conditions are adjusted appropriately, the gas can be made to trace out a Carnot cycle in P-V space.
    [Show full text]
  • Pressure Vessels
    PRESSURE VESSELS David Roylance Department of Materials Science and Engineering Massachusetts Institute of Technology Cambridge, MA 02139 August 23, 2001 Introduction A good deal of the Mechanics of Materials can be introduced entirely within the confines of uniaxially stressed structural elements, and this was the goal of the previous modules. But of course the real world is three-dimensional, and we need to extend these concepts accordingly. We now take the next step, and consider those structures in which the loading is still simple, but where the stresses and strains now require a second dimension for their description. Both for their value in demonstrating two-dimensional effects and also for their practical use in mechanical design, we turn to a slightly more complicated structural type: the thin-walled pressure vessel. Structures such as pipes or bottles capable of holding internal pressure have been very important in the history of science and technology. Although the ancient Romans had developed municipal engineering to a high order in many ways, the very need for their impressive system of large aqueducts for carrying water was due to their not yet having pipes that could maintain internal pressure. Water can flow uphill when driven by the hydraulic pressure of the reservoir at a higher elevation, but without a pressure-containing pipe an aqueduct must be constructed so the water can run downhill all the way from the reservoir to the destination. Airplane cabins are another familiar example of pressure-containing structures. They illus- trate very dramatically the importance of proper design, since the atmosphere in the cabin has enough energy associated with its relative pressurization compared to the thin air outside that catastrophic crack growth is a real possibility.
    [Show full text]
  • CHAPTER 17 Internal Pressure and Internal Energy of Saturated and Compressed Phases Ainstitute of Physics of the Dagestan Scient
    CHAPTER 17 Internal Pressure and Internal Energy of Saturated and Compressed Phases ILMUTDIN M. ABDULAGATOV,a,b JOSEPH W. MAGEE,c NIKOLAI G. POLIKHRONIDI,a RABIYAT G. BATYROVAa aInstitute of Physics of the Dagestan Scientific Center of the Russian Academy of Sciences, Makhachkala, Dagestan, Russia. E-mail: [email protected] bDagestan State University, Makhachkala, Dagestan, Russia cNational Institute of Standards and Technology, Boulder, Colorado 80305 USA. E- mail: [email protected] Abstract Following a critical review of the field, a comprehensive analysis is provided of the internal pressure of fluids and fluid mixtures and its determination in a wide range of temperatures and pressures. Further, the physical meaning is discussed of the internal pressure along with its microscopic interpretation by means of calorimetric experiments. A new relation is explored between the internal pressure and the isochoric heat capacity jump along the coexistence curve near the critical point. Various methods (direct and indirect) of internal pressure determination are discussed. Relationships are studied between the internal pressure and key thermodynamic properties, namely expansion coefficient, isothermal compressibility, speed of sound, enthalpy increments, and viscosity. Loci of isothermal, isobaric, and isochoric internal pressure maxima and minima were examined in addition to the locus of zero internal pressure. Details were discussed of the new method of direct internal pressure determination by a calorimetric experiment that involves simultaneous measurement of the thermal pressure coefficient (∂P / ∂T )V , i.e. internal pressure Pint = (∂U / ∂V )T and heat capacity cV = (∂U / ∂T )V . The dependence of internal pressure on external pressure, temperature and density for pure fluids, and on concentration for binary mixtures is considered on the basis of reference (NIST REFPROP) and crossover EOS.
    [Show full text]