DOCSLIB.ORG

Chapter 3. Second and Third Law of Thermodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 3. Second and Third Law of Thermodynamics Chapter 3. Second and third law of thermodynamics Important Concepts Review Entropy; Gibbs Free Energy • Entropy (S) – definitions Law of Corresponding States (ch 1 notes) • Entropy changes in reversible and Reduced pressure, temperatures, volumes irreversible processes • Entropy of mixing of ideal gases • 2nd law of thermodynamics • 3rd law of thermodynamics Math • Free energy Numerical integration by computer • Maxwell relations (Trapezoidal integration • Dependence of free energy on P, V, T https://en.wikipedia.org/wiki/Trapezoidal_rule) • Thermodynamic functions of mixtures Properties of partial differential equations • Partial molar quantities and chemical Rules for inequalities potential Major Concept Review • Adiabats vs. isotherms p1V1 p2V2 • Sign convention for work and heat w done on c=C /R vm system, q supplied to system : + p1V1 p2V2 =Cp/CV w done by system, q removed from system : c c V1T1 V2T2 - • Joule-Thomson expansion (DH=0); • State variables depend on final & initial state; not Joule-Thomson coefficient, inversion path. temperature • Reversible change occurs in series of equilibrium V states T TT V P p • Adiabatic q = 0; Isothermal DT = 0 H CP • Equations of state for enthalpy, H and internal • Formation reaction; enthalpies of energy, U reaction, Hess’s Law; other changes D rxn H iD f Hi i T D rxn H Drxn Href DrxnCpdT Tref • Calorimetry Spontaneous and Nonspontaneous Changes First Law: when one form of energy is converted to another, the total energy in universe is conserved. • Does not give any other restriction on a process • But many processes have a natural direction Examples • gas expands into a vacuum; not the reverse • can burn paper; can't unburn paper • heat never flows spontaneously from cold to hot These changes are called nonspontaneous changes. It is useful to predict whether a physical/chemical change will go spontaneously in the forward or backward direction. The second law and entropy, S, a state function of the system, is what tells us this. Carnot, investigating heat engines, was the first to answer the question of spontaneity. Nicolas Léonard Sadi Carnot 1796-1832 "father of thermodynamics" The Carnot Engine and Carnot Cycle A heat engine is an engine that uses heat to generate mechanical work by carrying a "working substance" through a cyclic process. A quantity of heat qh is withdrawn from the hot reservoir (the boiler) A quantity of heat qc (negative by convention) is discharged to the cold reservoir (the condenser) the work done by the engine is w (negative by convention). The Carnot Engine and Carnot Cycle http://galileoandeinstein.physics.virginia.edu/mor e_stuff/flashlets/carnot.htm Carnot Heat Engines Step 1: Reversible, isothermal expansion from A to B at Th ∆U1 = 푞ℎ + 푤1 = 0 (isothermal, ideal gas) Heat= 푞ℎ 푉퐵 Work 푤1 = −푅푇ℎ푙푛 = −푞ℎ 푉퐴 Step 2: Reversible, adiabatic expansion from B to C; Th→Tc Heat= 푞 = 0(adiabatic) 푇푐 Work 푤2 = ∆푈2 = ׬ 퐶푣푑푇 푇ℎ 푇푐 퐶 푚 푉 න 푣 푑푇 = −Rln 퐶 푇 푉퐵 푇ℎ Step 4: Reversible, adiabatic compression from D to Step 3: Reversible, isothermal compression from C to D at Tc A; Tc→Th Heat= 푞 = 0(adiabatic) ℎ ∆U1 = 푞푐 + 푤3 = 0 (isothermal, ideal gas) Work 푤4 = ∆푈4 = ׬ 퐶푣푑푇 Heat= 푞 (negative because heat is leaving the system) 푇푐 푐 푇ℎ 푉퐷 퐶 푚 푉 Work 푤3 = −푅푇푐푙푛 = −푞푐 푣 퐴 푉퐶 න 푑푇 = −Rln 푇 푉퐷 푇푐 Efficiency of Heat Engine ∆U퐶푌퐶퐿 = 0 = 푞ℎ+푞퐶 + 푤1 + 푤2 + 푤3 + 푤4 = 푞푐푦푐푙+푤퐶푦푐푙 −푤퐶푦푐푙= 푞푐푦푐푙 = 푞ℎ + 푞퐶 푤표푟푘 푝푒푟푓표푟푚푒푑 −푤 푞 푞 푞 Efficiency: = 퐶푦푐푙= ℎ+ 퐶 = 1 − 퐶 ≡ 휂. ℎ푒푎푡 푠푢푝푝푙푒푑 푞ℎ 푞ℎ 푞ℎ 푇 퐶 푚 푉 푉 Comparing adiabatic steps: ׬ ℎ 푣 푑푇 = −Rln 퐵 = −Rln 퐴 푇푐 푇 푉퐶 푉퐷 푉 푉 푉 푉 푉 푉 Ratios of volumes are equal: 퐵 = 퐴, so 퐶 = 퐵, so −ln 퐷 = ln 퐵 푉퐶 푉퐷 푉퐷 푉퐴 푉퐶 푉퐴 푉퐵 푉퐷 푉퐵 Can not rewrite heats: 푅푇ℎ푙푛 = 푞ℎ ; 푅푇푐푙푛 = 푞푐=−푅푇푐푙푛 푉퐴 푉퐶 푉퐴 푞 푞 푞 푞 Therefore, 푐 = − ℎ 푎푛푑 푐 + ℎ = 0 푇푐 푇ℎ 푇푐 푇ℎ Means two things: 1) Even though q is not a state function, q/T is! 푑푞 We define this as entropy 푑푆 ≡ 푟푒푣 푇 Although a change in S must be calculated along a reversible path, entropy can be defined for any process 푇 푇 −푇 2) Can use T in efficiency calculation. 휂 = 1 − 푐 = ℎ 푐 푇ℎ 푇ℎ Heat Engines and Refrigerators Operate Heat Engine in Reverse Supply work to system Remove heat from cold reservoir, and add it to hot reservoir Work required to furnish heat qh with a heat pump 푇ℎ − 푇푐 푤 = −푞ℎ 푇ℎ Ratio of work required to remove heat qc with a/c or refrigerator 푤 푇ℎ − 푇푐 = 푞푐 푇푐 푞푐 푇푐 Coefficient of performance 푐 = = 푤 푇ℎ − 푇푐 Definition of entropy (S) Thermodynamic definition – entropy is related to the heat flow f dS= dq /T , DS 1 T dq rev rev i e.g. DS for isothermal reversible expansion of ideal gas: DU = q+w = 0, so, qrev = -wrev = nRT ln(Vf/Vi) DS = qrev/T = nR ln(Vf/Vi) Statistical definition of entropy (S) Statistical definition – entropy is related to the probability Entropy is a measure of the number of possible microscopic states of a system. S=k ln W (k: Boltzmann constant, W: number of microstates W) W is a measure of disorder of the system in a sense. e.g. There is only one way to have 100 coins with all heads up: W=1 There are 100891344545564193334812497256 ways to have half of the coins are heads up: W=100891344545564193334812497256 – a lot more probable. http://www.bbc.com/earth/story/20150309-why-does-time-only-run-forwards Inequality of Clausius The second law discusses the properties of entropy. • Start with First Law dU dq PexdV • For a reversible process, P = Pex & dq = TdS • Gives dU TdS PdV (true for any process, reversible or not since S and U are state variables) • Now use dU = dq + dw • equate 2 equations for dU TdS PdV dq PexdV TdS dq P Pex dV If P > Pex , sys. will expand, dV > 0, 2nd term is + If P < Pex , sys. will contract, dV < 0, 2nd term is + If P = Pex , 2nd term = 0 (equilibrium) Therefore, TdS dq Second Law • If the process is reversible, the equality applies Rudolf Julius • If any part of the process is irreversible, the inequality applies Emanuel Clausius 2 It is impossible for dS dq T January 1822 – 24 August 1888) In an isolated system, dq = 0 DS > 0 spontaneous, irreversible process DS = 0 reversible process DS < 0 impossible process! Second law of thermodynamics - direction of spontaneous change Spontaneous changes occurs in the direction where the energy of isolated system is dispersed in a random, chaotic way. 2nd Law: Total entropy of an isolated system increases in the course of a spontaneous change. DStot >0 You can't break even. dU w q Can't convert all energy to work. q TdS Even in a perfectly efficient system, lose some to entropy. For a reversible system, dU TdS w http://www.bbc.com/earth/story/20150309-why-does-time-only-run-forwards Entropy of System and Surroundings The second law does not say that the entropy of a system can never spontaneously decrease. It does say that the entropy of the universe can never decrease. So, if in a spontaneous process, the entropy of the system goes down, then the entropy of the surroundings must go up. dSsur= dqsur, rev/T , dSsur= dqsur/T To predict spontaneity in a system that is not isolated, must calculate both entropy of system and surroundings. • Surroundings typically very large, and V or P is constant. • Heat transferred to the surrounding is dU or dH, state function – same regardless of reversible path or not. • Entropy change in surroundings can be simply calculated from the heat transferred to the surroundings and its temperature. dSsys = dqsys, rev/T • For reversible process, heat can be used to calculate the entropy change. • For irreversible process, find a reversible path having the same initial and final state. Example of entropy change system & surroundings (reversible case) Reversible isothermal compression of ideal gas 22.4 L of gas compressed to 11.2 L at 273K • For system, DU = 0, qrev = -w = nRTln(Vf/Vi) = 8.314 x 273 ln(1/2) = -1573J DS = qrev /T, -1573/273 = -5.76 J/K (entropy of system decreased) • For surroundings, Heat is added to the surrounding from the system, qsur = - qrev DSsur = qsurv /T, 1573/273 = 5.76 J/K (entropy of surroundings increased) • Total entropy change DStotal = DSsys + DSsur = -5.76 J/K + 5.76 J/K = 0 J/K Total entropy change is zero for a reversible process ! Example of entropy change system & surroundings (irreversible case) Isothermal compression of ideal gas (P1V1=P2V2) initially at 1 atm 22.4 L of gas compressed to 11.2 L at 273K with external pressure same as final pressure • For system, Calculate heat for the reversible path with same initial and final states. Entropy change in the system is the same as in the previous page. -5.76 J/K • For surroundings, must know how much heat is transferred DSsur = qsur /T = - qsys/T, qsys can be calculated by looking at system. DU = 0, qsys = -w = Pext DV = 2 atm x101.325 J/L-atm· (-11.2 L)= -2270J DSsur = 2270/273 = 8.31 J/K • Total entropy change DStotal = DSsys + DSsur = -5.76 J/K + 8.31 J/K = 2.55 J/K Total entropy change is positive for an irreversible process ! Calculating Entropy Changes dU PdV 푑푈 = 푑푞 + 푑푤 to get dS T I.
Load more

Recommended publications
  • ENERGY, ENTROPY, and INFORMATION Jean Thoma June
    ENERGY, ENTROPY, AND INFORMATION Jean Thoma June 1977 Research Memoranda are interim reports on research being conducted by the International Institute for Applied Systems Analysis, and as such receive only limited scientific review. Views or opinions contained herein do not necessarily represent those of the Institute or of the National Member Organizations supporting the Institute. PREFACE This Research Memorandum contains the work done during the stay of Professor Dr.Sc. Jean Thoma, Zug, Switzerland, at IIASA in November 1976. It is based on extensive discussions with Professor HAfele and other members of the Energy Program. Al- though the content of this report is not yet very uniform because of the different starting points on the subject under consideration, its publication is considered a necessary step in fostering the related discussion at IIASA evolving around th.e problem of energy demand. ABSTRACT Thermodynamical considerations of energy and entropy are being pursued in order to arrive at a general starting point for relating entropy, negentropy, and information. Thus one hopes to ultimately arrive at a common denominator for quanti- ties of a more general nature, including economic parameters. The report closes with the description of various heating appli- cation.~and related efficiencies. Such considerations are important in order to understand in greater depth the nature and composition of energy demand. This may be highlighted by the observation that it is, of course, not the energy that is consumed or demanded for but the informa- tion that goes along with it. TABLE 'OF 'CONTENTS Introduction ..................................... 1 2 . Various Aspects of Entropy ........................2 2.1 i he no me no logical Entropy ........................
    [Show full text]
  • Lecture 4: 09.16.05 Temperature, Heat, and Entropy
    3.012 Fundamentals of Materials Science Fall 2005 Lecture 4: 09.16.05 Temperature, heat, and entropy Today: LAST TIME .........................................................................................................................................................................................2� State functions ..............................................................................................................................................................................2� Path dependent variables: heat and work..................................................................................................................................2� DEFINING TEMPERATURE ...................................................................................................................................................................4� The zeroth law of thermodynamics .............................................................................................................................................4� The absolute temperature scale ..................................................................................................................................................5� CONSEQUENCES OF THE RELATION BETWEEN TEMPERATURE, HEAT, AND ENTROPY: HEAT CAPACITY .......................................6� The difference between heat and temperature ...........................................................................................................................6� Defining heat capacity.................................................................................................................................................................6�
    [Show full text]
  • A Simple Method to Estimate Entropy and Free Energy of Atmospheric Gases from Their Action
    Article A Simple Method to Estimate Entropy and Free Energy of Atmospheric Gases from Their Action Ivan Kennedy 1,2,*, Harold Geering 2, Michael Rose 3 and Angus Crossan 2 1 Sydney Institute of Agriculture, University of Sydney, NSW 2006, Australia 2 QuickTest Technologies, PO Box 6285 North Ryde, NSW 2113, Australia; [email protected] (H.G.); [email protected] (A.C.) 3 NSW Department of Primary Industries, Wollongbar NSW 2447, Australia; [email protected] * Correspondence: [email protected]; Tel.: + 61-4-0794-9622 Received: 23 March 2019; Accepted: 26 April 2019; Published: 1 May 2019 Abstract: A convenient practical model for accurately estimating the total entropy (ΣSi) of atmospheric gases based on physical action is proposed. This realistic approach is fully consistent with statistical mechanics, but reinterprets its partition functions as measures of translational, rotational, and vibrational action or quantum states, to estimate the entropy. With all kinds of molecular action expressed as logarithmic functions, the total heat required for warming a chemical system from 0 K (ΣSiT) to a given temperature and pressure can be computed, yielding results identical with published experimental third law values of entropy. All thermodynamic properties of gases including entropy, enthalpy, Gibbs energy, and Helmholtz energy are directly estimated using simple algorithms based on simple molecular and physical properties, without resource to tables of standard values; both free energies are measures of quantum field states and of minimal statistical degeneracy, decreasing with temperature and declining density. We propose that this more realistic approach has heuristic value for thermodynamic computation of atmospheric profiles, based on steady state heat flows equilibrating with gravity.
    [Show full text]
  • Calculating the Configurational Entropy of a Landscape Mosaic
    Landscape Ecol (2016) 31:481–489 DOI 10.1007/s10980-015-0305-2 PERSPECTIVE Calculating the configurational entropy of a landscape mosaic Samuel A. Cushman Received: 15 August 2014 / Accepted: 29 October 2015 / Published online: 7 November 2015 Ó Springer Science+Business Media Dordrecht (outside the USA) 2015 Abstract of classes and proportionality can be arranged (mi- Background Applications of entropy and the second crostates) that produce the observed amount of total law of thermodynamics in landscape ecology are rare edge (macrostate). and poorly developed. This is a fundamental limitation given the centrally important role the second law plays Keywords Entropy Á Landscape Á Configuration Á in all physical and biological processes. A critical first Composition Á Thermodynamics step to exploring the utility of thermodynamics in landscape ecology is to define the configurational entropy of a landscape mosaic. In this paper I attempt to link landscape ecology to the second law of Introduction thermodynamics and the entropy concept by showing how the configurational entropy of a landscape mosaic Entropy and the second law of thermodynamics are may be calculated. central organizing principles of nature, but are poorly Result I begin by drawing parallels between the developed and integrated in the landscape ecology configuration of a categorical landscape mosaic and literature (but see Li 2000, 2002; Vranken et al. 2014). the mixing of ideal gases. I propose that the idea of the Descriptions of landscape patterns, processes of thermodynamic microstate can be expressed as unique landscape change, and propagation of pattern-process configurations of a landscape mosaic, and posit that relationships across scale and through time are all the landscape metric Total Edge length is an effective governed and constrained by the second law of measure of configuration for purposes of calculating thermodynamics (Cushman 2015).
    [Show full text]
  • Thermodynamics
    ME346A Introduction to Statistical Mechanics { Wei Cai { Stanford University { Win 2011 Handout 6. Thermodynamics January 26, 2011 Contents 1 Laws of thermodynamics 2 1.1 The zeroth law . .3 1.2 The first law . .4 1.3 The second law . .5 1.3.1 Efficiency of Carnot engine . .5 1.3.2 Alternative statements of the second law . .7 1.4 The third law . .8 2 Mathematics of thermodynamics 9 2.1 Equation of state . .9 2.2 Gibbs-Duhem relation . 11 2.2.1 Homogeneous function . 11 2.2.2 Virial theorem / Euler theorem . 12 2.3 Maxwell relations . 13 2.4 Legendre transform . 15 2.5 Thermodynamic potentials . 16 3 Worked examples 21 3.1 Thermodynamic potentials and Maxwell's relation . 21 3.2 Properties of ideal gas . 24 3.3 Gas expansion . 28 4 Irreversible processes 32 4.1 Entropy and irreversibility . 32 4.2 Variational statement of second law . 32 1 In the 1st lecture, we will discuss the concepts of thermodynamics, namely its 4 laws. The most important concepts are the second law and the notion of Entropy. (reading assignment: Reif x 3.10, 3.11) In the 2nd lecture, We will discuss the mathematics of thermodynamics, i.e. the machinery to make quantitative predictions. We will deal with partial derivatives and Legendre transforms. (reading assignment: Reif x 4.1-4.7, 5.1-5.12) 1 Laws of thermodynamics Thermodynamics is a branch of science connected with the nature of heat and its conver- sion to mechanical, electrical and chemical energy. (The Webster pocket dictionary defines, Thermodynamics: physics of heat.) Historically, it grew out of efforts to construct more efficient heat engines | devices for ex- tracting useful work from expanding hot gases (http://www.answers.com/thermodynamics).
    [Show full text]
  • Chemistry C3102-2006: Polymers Section Dr. Edie Sevick, Research School of Chemistry, ANU 5.0 Thermodynamics of Polymer Solution
    Chemistry C3102-2006: Polymers Section Dr. Edie Sevick, Research School of Chemistry, ANU 5.0 Thermodynamics of Polymer Solutions In this section, we investigate the solubility of polymers in small molecule solvents. Solubility, whether a chain goes “into solution”, i.e. is dissolved in solvent, is an important property. Full solubility is advantageous in processing of polymers; but it is also important for polymers to be fully insoluble - think of plastic shoe soles on a rainy day! So far, we have briefly touched upon thermodynamic solubility of a single chain- a “good” solvent swells a chain, or mixes with the monomers, while a“poor” solvent “de-mixes” the chain, causing it to collapse upon itself. Whether two components mix to form a homogeneous solution or not is determined by minimisation of a free energy. Here we will express free energy in terms of canonical variables T,P,N , i.e., temperature, pressure, and number (of moles) of molecules. The free energy { } expressed in these variables is the Gibbs free energy G G(T,P,N). (1) ≡ In previous sections, we referred to the Helmholtz free energy, F , the free energy in terms of the variables T,V,N . Let ∆Gm denote the free eneregy change upon homogeneous mix- { } ing. For a 2-component system, i.e. a solute-solvent system, this is simply the difference in the free energies of the solute-solvent mixture and pure quantities of solute and solvent: ∆Gm G(T,P,N , N ) (G0(T,P,N )+ G0(T,P,N )), where the superscript 0 denotes the ≡ 1 2 − 1 2 pure component.
    [Show full text]
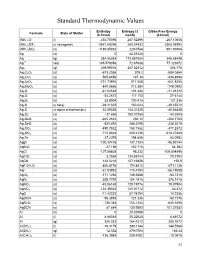
  • Standard Thermodynamic Values
    Standard Thermodynamic Values Enthalpy Entropy (J Gibbs Free Energy Formula State of Matter (kJ/mol) mol/K) (kJ/mol) (NH4)2O (l) -430.70096 267.52496 -267.10656 (NH4)2SiF6 (s hexagonal) -2681.69296 280.24432 -2365.54992 (NH4)2SO4 (s) -1180.85032 220.0784 -901.90304 Ag (s) 0 42.55128 0 Ag (g) 284.55384 172.887064 245.68448 Ag+1 (aq) 105.579056 72.67608 77.123672 Ag2 (g) 409.99016 257.02312 358.778 Ag2C2O4 (s) -673.2056 209.2 -584.0864 Ag2CO3 (s) -505.8456 167.36 -436.8096 Ag2CrO4 (s) -731.73976 217.568 -641.8256 Ag2MoO4 (s) -840.5656 213.384 -748.0992 Ag2O (s) -31.04528 121.336 -11.21312 Ag2O2 (s) -24.2672 117.152 27.6144 Ag2O3 (s) 33.8904 100.416 121.336 Ag2S (s beta) -29.41352 150.624 -39.45512 Ag2S (s alpha orthorhombic) -32.59336 144.01328 -40.66848 Ag2Se (s) -37.656 150.70768 -44.3504 Ag2SeO3 (s) -365.2632 230.12 -304.1768 Ag2SeO4 (s) -420.492 248.5296 -334.3016 Ag2SO3 (s) -490.7832 158.1552 -411.2872 Ag2SO4 (s) -715.8824 200.4136 -618.47888 Ag2Te (s) -37.2376 154.808 43.0952 AgBr (s) -100.37416 107.1104 -96.90144 AgBrO3 (s) -27.196 152.716 54.392 AgCl (s) -127.06808 96.232 -109.804896 AgClO2 (s) 8.7864 134.55744 75.7304 AgCN (s) 146.0216 107.19408 156.9 AgF•2H2O (s) -800.8176 174.8912 -671.1136 AgI (s) -61.83952 115.4784 -66.19088 AgIO3 (s) -171.1256 149.3688 -93.7216 AgN3 (s) 308.7792 104.1816 376.1416 AgNO2 (s) -45.06168 128.19776 19.07904 AgNO3 (s) -124.39032 140.91712 -33.472 AgO (s) -11.42232 57.78104 14.2256 AgOCN (s) -95.3952 121.336 -58.1576 AgReO4 (s) -736.384 153.1344 -635.5496 AgSCN (s) 87.864 130.9592 101.37832 Al (s)
    [Show full text]
  • Thermodynamic Entropy As an Indicator for Urban Sustainability?
    Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 00 (2017) 000–000 www.elsevier.com/locate/procedia Urban Transitions Conference, Shanghai, September 2016 Thermodynamic entropy as an indicator for urban sustainability? Ben Purvisa,*, Yong Maoa, Darren Robinsona aLaboratory of Urban Complexity and Sustainability, University of Nottingham, NG7 2RD, UK bSecond affiliation, Address, City and Postcode, Country Abstract As foci of economic activity, resource consumption, and the production of material waste and pollution, cities represent both a major hurdle and yet also a source of great potential for achieving the goal of sustainability. Motivated by the desire to better understand and measure sustainability in quantitative terms we explore the applicability of thermodynamic entropy to urban systems as a tool for evaluating sustainability. Having comprehensively reviewed the application of thermodynamic entropy to urban systems we argue that the role it can hope to play in characterising sustainability is limited. We show that thermodynamic entropy may be considered as a measure of energy efficiency, but must be complimented by other indices to form part of a broader measure of urban sustainability. © 2017 The Authors. Published by Elsevier Ltd. Peer-review under responsibility of the organizing committee of the Urban Transitions Conference. Keywords: entropy; sustainability; thermodynamics; city; indicators; exergy; second law 1. Introduction The notion of using thermodynamic concepts as a tool for better understanding the problems relating to “sustainability” is not a new one. Ayres and Kneese (1969) [1] are credited with popularising the use of physical conservation principles in economic thinking. Georgescu-Roegen was the first to consider the relationship between the second law of thermodynamics and the degradation of natural resources [2].
    [Show full text]
  • Chapter 19 Chemical Thermodynamics
    Chapter 19 Chemical Thermodynamics Entropy and free energy Learning goals and key skills: Explain and apply the terms spontaneous process, reversible process, irreversible process, and isothermal process. Define entropy and state the second law of thermodynamics. Calculate DS for a phase change. Explain how the entropy of a system is related to the number of possible microstates. Describe the kinds of molecular motion that a molecule can possess. Predict the sign of DS for physical and chemical processes. State the third law of thermodynamics. Compare the values of standard molar entropies. Calculate standard entropy changes for a system from standard molar entropies. Calculate the Gibbs free energy from the enthalpy change and entropy change at a given temperature. Use free energy changes to predict whether reactions are spontaneous. Calculate standard free energy changes using standard free energies of formation. Predict the effect of temperature on spontaneity given DH and DS. Calculate DG under nonstandard conditions. Relate DG°and equilibrium constant (K). Review Chapter 5: energy, enthalpy, 1st law of thermo Thermodynamics: the science of heat and work Thermochemistry: the relationship between chemical reactions and energy changes Energy (E) The capacity to do work or to transfer heat. Work (w) The energy expended to move an object against an opposing force. w = F d Heat (q) Derived from the movements of atoms and molecules (including vibrations and rotations). Enthalpy (H) Enthalpy is the heat absorbed (or released) by a system during a constant-pressure process. 1 0th Law of Thermodynamics If A is in thermal equilibrium with B, and B is in thermal equilibrium with C, then C is also in thermal equilibrium with A.
    [Show full text]
  • Lecture 6: Entropy
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 6: Entropy 1 Introduction In this lecture, we discuss many ways to think about entropy. The most important and most famous property of entropy is that it never decreases Stot > 0 (1) Here, Stot means the change in entropy of a system plus the change in entropy of the surroundings. This is the second law of thermodynamics that we met in the previous lecture. There's a great quote from Sir Arthur Eddington from 1927 summarizing the importance of the second law: If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equationsthen so much the worse for Maxwell's equations. If it is found to be contradicted by observationwell these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of ther- modynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation. Another possibly relevant quote, from the introduction to the statistical mechanics book by David Goodstein: Ludwig Boltzmann who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. There are many ways to dene entropy. All of them are equivalent, although it can be hard to see. In this lecture we will compare and contrast dierent denitions, building up intuition for how to think about entropy in dierent contexts. The original denition of entropy, due to Clausius, was thermodynamic.
    [Show full text]
  • Energy and Enthalpy Thermodynamics
    Energy and Energy and Enthalpy Thermodynamics The internal energy (E) of a system consists of The energy change of a reaction the kinetic energy of all the particles (related to is measured at constant temperature) plus the potential energy of volume (in a bomb interaction between the particles and within the calorimeter). particles (eg bonding). We can only measure the change in energy of the system (units = J or Nm). More conveniently reactions are performed at constant Energy pressure which measures enthalpy change, ∆H. initial state final state ∆H ~ ∆E for most reactions we study. final state initial state ∆H < 0 exothermic reaction Energy "lost" to surroundings Energy "gained" from surroundings ∆H > 0 endothermic reaction < 0 > 0 2 o Enthalpy of formation, fH Hess’s Law o Hess's Law: The heat change in any reaction is the The standard enthalpy of formation, fH , is the change in enthalpy when one mole of a substance is formed from same whether the reaction takes place in one step or its elements under a standard pressure of 1 atm. several steps, i.e. the overall energy change of a reaction is independent of the route taken. The heat of formation of any element in its standard state is defined as zero. o The standard enthalpy of reaction, H , is the sum of the enthalpy of the products minus the sum of the enthalpy of the reactants. Start End o o o H = prod nfH - react nfH 3 4 Example Application – energy foods! Calculate Ho for CH (g) + 2O (g) CO (g) + 2H O(l) Do you get more energy from the metabolism of 1.0 g of sugar or
    [Show full text]
  • Estimation of Internal Pressure of Liquids and Liquid Mixtures
    Available online at www.ilcpa.pl International Letters of Chemistry, Physics and Astronomy 5 (2012) 1-7 ISSN 2299-3843 Estimation of internal pressure of liquids and liquid mixtures N. Santhi 1, P. Sabarathinam 2, G. Alamelumangai 1, J. Madhumitha 1, M. Emayavaramban 1 1Department of Chemistry, Government Arts College, C.Mutlur, Chidambaram-608102, India 2Retd. Registrar & Head of the Department of Technology, Annamalai University, Annamalainagar-608002, India E-mail address: [email protected] ABSTRACT By combining the van der Waals’ equation of state and the Free Length Theory of Jacobson, a new theoretical model is developed for the prediction of internal pressure of pure liquids and liquid mixtures. It requires only the molar volume data in addition to the ratio of heat capacities and critical temperature. The proposed model is simple, reliably accurate and capable of predicting internal pressure of pure liquids with an average absolute deviation of 4.24% in the predicted internal pressure values compared to those given in literature. The average absolute deviation in the predicted internal pressure values through the proposed model for the five binary liquid mixtures tested varies from 0.29% to 1.9% when compared to those of literature values. Keywords: van der Waals, pressure of liquids, theory of Jacobson, capacity of heat liquids, equation of Srivastava and Berkowitz 1. INTRODUTION The importance of internal pressure in understanding the properties of liquids and the full potential of internal pressure as a structural probe did become apparent with the pioneering work of Hildebrand 1, 2 and the first review of the subject by Richards 3 appeared in 1925.
    [Show full text]