Data-Driven Dynamic Network Modeling for Analyzing the Evolution of Product Competitions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DX7 PRODUCT PROFILE PART 1 PART 2 Marketing Product
DX7 PRODUCT PROFILE PART 1 PART 2 marketing product CONTENTS 目录 2 PART 1 Marketing 1. marketing analysis 2. DX7 position 1. Marketing Analysis competitive products focused : l DX7,2700mm wheel base ,marches towards midsize car market. l Considering from the close entry price,wheel base and market share,we sum up some of the competitive products as below: benchmarking core competitive competitive product: product: Haval H6 ChanganCS75 4 1. Marketing Analysis competitive products focused : major competitive products: Pentium X80 DongFeng FengShenAX7 subordinate competitive Chery Tiggo5 BYD S6 product: 5 1. Marketing Analysis competitive products focused : subordinate competitive products: GAC TrumpchiGS4 VenuciaT70 JAC S5 6 2. DX7 position Hitting Directly the Target Market--- Marching towards A-Class SUV Marketing Hitiing on City SUV face to the opportunity: Market demand:the market potential for A-Class City SUV is remarkeable. 7 2. DX7 position Dedicated to creating SEM'S first Intelligent City Luxury SUV with global fashion shape、 international building cars quality and supassing the same level market . 8 2. DX7position All-Around Safety Super Configuration l C-NCAP five star safety design Fashion Design l APA automatic parking system standard,super high strengh cage body l designed by global famous design l AVM All-around View Monitor structure company ---Pininfarina l voice recognition system l positive safety l Pininfarina sport esthetics system(ESC/ROP/HDC/HSA) l EAGLE fairshape design l BSW l LED daytime running lamp+AFS Excellent -

Fakulta Strojní Ústav Automobilů, Spalovacích Motorů a Kolejových Vozidel
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ ÚSTAV AUTOMOBILŮ, SPALOVACÍCH MOTORŮ A KOLEJOVÝCH VOZIDEL PŘEHLED A TRENDY VE VÝVOJI PŘEVODOVEK OSOBNÍCH AUTOMOBILŮ OVERVIEW AND TRENDS IN THE DEVELOPMENT OF PASSENGER CAR TRANSMISSIONS BAKALÁŘSKÁ PRÁCE AUTOR PRÁCE: Monika Rémišová VEDOUCÍ PRÁCE: doc. Dr. Ing. Gabriela Achtenová AKADEMICKÝ ROK: 2017/2018 STUDIJNÍ PROGRAM: Strojírenství STUDIJNÍ OBOR: Konstruování podporované počítačem Prohlášení Prohlašuji, že jsem svou bakalářskou práci vypracovala samostatně a použila pouze podklady uvedené v přiloženém seznamu. Nemám závažný důvod proti užití tohoto díla ve smyslu § 60 Zákona č.121/2000 Sb., o právu autorském, o právech souvisejících s právem autorským a o změně některých zákonů (autorský zákon). V Praze dne 12. 7. 2018 …………………………………… Monika Rémišová Poděkování Ráda bych tímto chtěla poděkovat vedoucí mé bakalářské práce doc. Dr. Ing. Gabriele Achtenové za zájem, vedení, cenné rady a čas, který mi věnovala. Anotace RÉMIŠOVÁ M., Přehled a trendy ve vývoji převodovek osobních automobilů, Praha 6, 2018. Bakalářská práce na Strojní fakultě ČVUT v Praze. Vedoucí baka- lářské práce doc. Dr. Ing. Gabriela Achtenová. 47 stran, 3 obrázky, 27 grafů Bakalářská práce je zaměřena na převodové systémy, které byly používány v le- tech 1995 až 2016 v osobních automobilech. Jsou popsány funkce hybridních vo- zidel a jejich užití. Hlavním cílem je graficky zpracovat statistiku. Klíčová slova Statistika, převodovka, převodové ústrojí, pohon, osobní automobil Annotation RÉMIŠOVÁ M., Overview and trends in the development of passenger car transmissions, Prague 6, 2018. The Bechelor´s work at Machine faculty CTU in Prague. The supervisor of this bachelor´s work is doc. Dr. Ing. Gabriela Achtenová. 47 pages, 3 pictures, 27 graphs This bachelor´s work is specialized in gearbox that were used from 1995 to 2016 in passanger cars. -

QYT AUTO PARTS CO., LTD Email: [email protected] ; [email protected] Whatsapp: +86 13634216230 QYT No
QYT AUTO PARTS CO., LTD Email: [email protected] ; [email protected] WhatsApp: +86 13634216230 QYT no. Description Corss Ref. Application TOYOTA;LEXUS (SO0001‐SO0300) TOYOTA CAMRY ACV40 06‐12; SO0001 Steering Tie rod ends 45470‐09090 LEXUS LEXUS ES350/ES240 07‐ TOYOTA CAMRY ACV40 06‐12; SO0002 Steering Tie rod ends 45460‐09140 LEXUS LEXUS ES350/ES240 07‐ TOYOTA CAMRY SO0003 Steering Tie rod ends 45460‐09160 ACV50(2012‐) TOYOTA CAMRY SO0004 Steering Tie rod ends 45460‐09250 ACV50(2012‐) GEELY PANDA,HAIJING,GEELY YUANJING, YUANJING 18‐, SO0005 Steering Tie rod ends 45047‐49045 YUANJINGX3,GEELY EMGRAND EC7,GEELY ENGLON ,BINRUI;BYD F0,BYD F3/F3R/G3/G3R/L3;TOYOTA COROLLA;LIFAN LIFAN 620;JAC YUEYUE GEELY PANDA,HAIJING,GEELY YUANJING, YUANJING 18‐, SO0006 Steering Tie rod ends 45046‐49115 YUANJINGX3,GEELY EMGRAND EC7,GEELY ENGLON ,BINRUI;BYD F0,BYD F3/F3R/G3/G3R/L3;TOYOTA COROLLA;LIFAN LIFAN 620;JAC YUEYUE CHANGAN RAETON;TOYOTA CAMRY2.4/3.0 (03),PREVIA ACR30 (34M); SO0007 Steering Tie rod ends 45460‐39615 LEXUS ES300/MCV30 01‐06 CHANGAN RAETON;TOYOTA CAMRY2.4/3.0 (03),PREVIA ACR30 (34M); SO0008 Steering Tie rod ends 45470‐39215 LEXUS ES300/MCV30 01‐06 BYD SURUI,SONG MAX;ZOTYE Z300; SO0009 Steering Tie rod ends 45046‐09590 TOYOTA COROLLA 07‐/VERSO 11‐/LEVIN 14‐ BYD SURUI ,SONG MAX;ZOTYE Z300; SO0010 Steering Tie rod ends 45047‐09590 TOYOTA COROLLA 07‐/VERSO 11‐/LEVIN 14‐ SO0011 Steering Tie rod ends 45464‐30060 TOYOTA REIZ/CROWN;LEXUS LEXUS IS250/300 06‐,GS300/350/430 05‐ SO0012 Steering Tie rod ends 45463‐30130 TOYOTA REIZ/CROWN;LEXUS LEXUS -

Evidence from Chinese Electric Automotive Industry Leader BYD
2016 Proceedings of PICMET '16: Technology Management for Social Innovation Catching Up in a Bidirectional Way: Evidence from Chinese Electric Automotive Industry Leader BYD Bowen Zhang, Xianjun Li, Donghui Meng, Lewis Liu Department of Automotive Engineering, State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing, P. R. China Abstract--To catch up with leaders, whether latecomers for industrial practice, as some latecomer firms do use both should follow an “imitation to innovation” path or an ways to catch up at the same time. One important reason for “innovating to leapfrog” path is still not quite clear. To shine this gap between theory and practice is that the technology a some light on this issue, we focus on the case of BYD, a latecomer firm needs for catching up at a certain stage is latecomer growing from nobody to the pioneer of Chinese usually treated as a whole. In fact, the technology consists of electric automotive industry and the champion in world electric vehicle sales in a dozen years. We find that BYD catches up in a different parts, a latecomer firm may be weak in most of the bidirectional way by which it has kept doing imitation and technology that it needs to learn from imitation, but it may be innovation from the start and made them well balanced to relatively strong in a certain technology that it can do R&D achieve the best of cost performance. This is different from the and innovate. In other words, latecomer firms may not catch unidirectional view that a latecomers’ catching-up either starts up in a unidirectional way, either imitation or innovation, but from a reverse innovation way like "from imitation to in a bidirectional way that they do imitation and innovation at innovation", or from a leapfrogging way that requires the same time. -

Electrifying the World's Largest New Car Market; Reinstate At
August 31, 2016 ACTION Buy BYD Co. (1211.HK) Return Potential: 15% Equity Research Electrifying the world’s largest new car market; reinstate at Buy Source of opportunity Investment Profile Electrification is set to reshape China’s auto market and we expect BYD to Low High lead this trend given its strong product portfolio, vertically integrated model Growth Growth and high OPM vs. peers. A comparative analysis with Tesla shows many Returns * Returns * strategic similarities but BYD’s new energy vehicle business trades at a sizable Multiple Multiple discount, which we see as unjustified given its large cost savings, capacity Volatility Volatility utilization, and front-loaded investment. China’s new energy vehicle market is Percentile 20th 40th 60th 80th 100th poised to deliver c.30% CAGR (vs. 4% for traditional cars) over the next decade. BYD Co. (1211.HK) We have removed the RS designation from BYD. It is on the Buy List with a Asia Pacific Autos & Autoparts Peer Group Average * Returns = Return on Capital For a complete description of the investment 12-m TP of HK$61.93, implying 15% upside. Our scenario analysis, flexing profile measures please refer to the disclosure section of this document. sales volume and margin assumptions, implies a further 30% valuation upside. Catalyst Key data Current Price (HK$) 54.00 1) More cities in China are likely to announce local preferential policies in 12 month price target (HK$) 61.93 Market cap (HK$ mn / US$ mn) 110,705.4 / 14,270.1 the new energy vehicle (NEV) segment once the result of the subsidy fraud Foreign ownership (%) -- probe is announced. -

Data-Driven Dynamic Network Modeling for Analyzing the Evolution of Product Competitions
Jian Xie School of Mechanical Engineering, Beijing Institute of Technology, 5 South Zhonguancun Street, Haidian District, Beijing 100081, China e-mail: [email protected] Youyi Bi University of Michigan-Shanghai Jiao Tong University Joint Institute, Downloaded from http://asmedigitalcollection.asme.org/mechanicaldesign/article-pdf/142/3/031112/6649149/md_142_3_031112.pdf by Northwestern University, Yaxin Cui on 19 May 2021 Shanghai Jiao Tong University, 800 Dong Chuan Road, Shanghai 200240, China e-mail: [email protected] Data-Driven Dynamic Network Zhenghui Sha System Integration & Design Modeling for Analyzing the Informatics Laboratory, University of Arkansas, Evolution of Product Competitions 863 West Dickson Street, Fayetteville, AR 72701 Understanding the impact of engineering design on product competitions is imperative for e-mail: [email protected] product designers to better address customer needs and develop more competitive products. In this paper, we propose a dynamic network-based approach for modeling and analyzing Mingxian Wang the evolution of product competitions using multi-year buyer survey data. The product co- Global Data Insight & Analytics, consideration network, formed based on the likelihood of two products being co-considered Ford Motor Company, from survey data, is treated as a proxy of products’ competition relations in a market. The Dearborn, MI 48120 separate temporal exponential random graph model (STERGM) is employed as the dynamic e-mail: [email protected] network modeling technique to model the evolution of network as two separate processes: link formation and link dissolution. We use China’s automotive market as a case study to Yan Fu illustrate the implementation of the proposed approach and the benefits of dynamic Global Data Insight & Analytics, network models compared to the static network modeling approach based on an exponential Ford Motor Company, random graph model (ERGM). -

Auto Pricelist 2020 3 16 Hyundai, Suzuki, Mazda, MG And
BRAND: TOYOTA PRICE TOYOTA ALPHARD 3.5L GAS A/T 3,740,000.00 TOYOTA ALPHARD 3.5L GAS A/T (WHITE PEARL) 3,755,000.00 TOYOTA ALTIS 1.6E GAS M/T 999,000.00 TOYOTA ALTIS 1.6G GAS A/T MC 1,115,000.00 TOYOTA ALTIS 1.6G GAS M/T MC 1,045,000.00 TOYOTA ALTIS 1.6V GAS A/T MC 1,185,000.00 TOYOTA ALTIS 1.6V GAS A/T MC (WHITE PEARL) 1,200,000.00 TOYOTA ALTIS 1.8V HV CVT 1,580,000.00 TOYOTA ALTIS 2.0V GAS A/T 1,477,000.00 TOYOTA ALTIS 2.0V GAS A/T (WHITE PEARL) 1,492,000.00 TOYOTA AVANZA 1.3E GAS A/T 919,000.00 TOYOTA AVANZA 1.3E GAS M/T 876,000.00 TOYOTA AVANZA 1.3J GAS M/T 743,000.00 TOYOTA AVANZA 1.5G GAS A/T 1,012,000.00 TOYOTA AVANZA 1.5G GAS M/T 969,000.00 TOYOTA AVANZA 1.5G VELOZ A/T 1,077,000.00 TOYOTA CAMRY 2.5G GAS A/T 1,806,000.00 TOYOTA CAMRY 2.5G GAS A/T (WHITE PEARL) 1,821,000.00 TOYOTA CAMRY 2.5S GAS A/T 1,855,000.00 TOYOTA CAMRY 2.5S GAS A/T (WHITE PEARL) 1,870,000.00 TOYOTA CAMRY 2.5V GAS A/T 1,992,000.00 TOYOTA CAMRY 2.5V GAS A/T (WHITE PEARL) 2,007,000.00 TOYOTA CAMRY 3.5Q V6 GAS A/T 2,175,000.00 TOYOTA CAMRY 3.5Q V6 GAS A/T (WHITE PEARL) 2,190,000.00 TOYOTA COASTER 29-SEATER DSL M/T 3,618,000.00 TOYOTA FJ CRUISER 4.0L V6 GAS 4X4 A/T 2,083,000.00 TOYOTA FORTUNER 2.4 DSL A/T TRD 1,831,000.00 TOYOTA FORTUNER 2.4 DSL A/T TRD (WHITE PEARL) 1,846,000.00 TOYOTA FORTUNER 2.4G 4X2 DSL A/T 1,723,000.00 TOYOTA FORTUNER 2.4G 4X2 DSL M/T 1,633,000.00 TOYOTA FORTUNER 2.4V 4X2 DSL A/T 1,947,000.00 TOYOTA FORTUNER 2.4V 4X2 DSL A/T (WHITE PEARL) 1,962,000.00 TOYOTA FORTUNER 2.7G GAS 4X2 A/T 1,638,000.00 TOYOTA FORTUNER 2.8V 4X4 DSL A/T 2,286,000.00 -
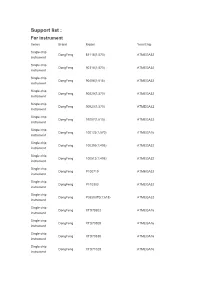
Support List : for Instrument Series Brand Model Year/Chip
Support list : For instrument Series Brand Model Year/Chip Single chip DongFeng 81118(1;570) ATMEGA32 instrument Single chip DongFeng 90318(1;570) ATMEGA32 instrument Single chip DongFeng 90408(1;615) ATMEGA32 instrument Single chip DongFeng 90820(1;570) ATMEGA32 instrument Single chip DongFeng 90923(1;570) ATMEGA32 instrument Single chip DongFeng 91007(1;615) ATMEGA32 instrument Single chip DongFeng 100123(1;570) ATMEGA16 instrument Single chip DongFeng 100305(1;495) ATMEGA32 instrument Single chip DongFeng 100512(1;495) ATMEGA32 instrument Single chip DongFeng P100719 ATMEGA32 instrument Single chip DongFeng P110303 ATMEGA32 instrument Single chip DongFeng P3820070(1;615) ATMEGA32 instrument Single chip DongFeng XTD70802 ATMEGA16 instrument Single chip DongFeng XTD70808 ATMEGA16 instrument Single chip DongFeng XTD70830 ATMEGA16 instrument Single chip DongFeng XTD71028 ATMEGA16 instrument Single chip DongFeng XTD71105 ATMEGA32 instrument Single chip DongFeng XTD80516 ATMEGA32 instrument Single chip DongFeng XTD90818 ATMEGA32 V1 instrument Single chip DongFeng XTD91126 ATMEGA32 instrument Single chip DongFeng XTD120814 ATMEGA32 instrument Single chip FOTON Auman ATMEGA32 instrument Single chip FuDi ZB157J1D1 ATMEGA16 instrument Single chip HaFei Zhongyi ATMEGA169 instrument Single chip Geely ZB156A ATMEGA169 V1 instrument Single chip Geely ZB127LS ATMEGA169 V1 instrument Single chip Geely ZB137LZ ATMEGA169 instrument Single chip Geely ZB118TYJ ATMEGA16 instrument Single chip Geely ZB106 ATMEGA16 instrument Single chip Geely ZB118 ATMEGA16 -

Green Car Congress: BYD's Qin Plug-In Hybrid the Best Selling
24 June 2014 Go to GCC Discussions forum About GCC Contact RSS Subscribe Twitter headlines « DOI: latest Gulf of Mexico oil & gas lease sales garner $872M in high bids | Main | Average Carbon Intensity of crude to California refineries in 2012 down very slightly from 2010 baseline » Print this post BYD’s Qin plug-in hybrid the best selling automotive EV in Google China Search 21 March 2014 GCC Web BYD’s second-generation Dual-Mode, plug-in hybrid electric sedan Qin has posted a second month of strong sales in February. Trends in March now make it “China’s Best-Selling Tweets From the Editor (different than Electric Vehicle” according to China’s National Passenger Car @GreenCarCongres headlines in Association. In the first weeks of 2014, more than 6,000 Qin horizontal menu) vehicles were sold, accounting for more than one-half of 2nd-generation Dual Mode (DM II) the Chinese new-energy vehicle market. plug-in hy brid sy stem of the Q in. C lick to enlarge. Analysts are not expecting sales to slow, as both Shanghai and Beijing announced earlier this month that they will now permit BYD new energy vehicles to qualify for local municipality green-vehicle incentives and be licensed in those regions. BYD’s Q in. C lick to enlarge. The Qin combines a 1.5-liter, turbocharged, direct-injection 4-cylinder, 113 kW (152 hp), 240 N·m (177 lb-ft) engine with a 110 kW (148 hp), 250 N·m (184 lb-ft) electric motor; combined system power is 217 kW (291 hp) maximum with 479 N·m (353 lb-ft) maximum torque. -

Proceedings Of
DRAFT Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference IDETC/CIE2019 August 18-21, 2019, Anaheim, CA, USA IDETC2019- 98385 DATA-DRIVEN DYNAMIC NETWORK MODELING FOR ANALYZING THE EVOLUTION OF PRODUCT COMPETITIONS Jian Xie Youyi Bi Zhenghui Sha Industrial Engineering Laboratory Integrated Design Automation System Integration & Design Beijing Institute of Technoloty Laboratory Informatics Laboratory Beijing, China Northwestern University University of Arkansas Evanston, IL, USA Fayetteville, AR, USA Mingxian Wang, Yan Fu Noshir Contractor Lin Gong Wei Chen1 Ford Analytics Science of Networks in Industrial Engineering Integrated Design Global Data Insight & Communities Laboratory Automation Laboratory Analytics Northwestern University Beijing Institute of Northwestern University Ford Motor Company Evanston, IL, USA Technoloty Evanston, IL, USA Dearborn, MI, USA Beijing, China ABSTRACT interpret the dynamic network-based models in studying Understanding the impact of engineering design on product temporal changes in product competition relations. competitions is imperative for product designers to better Keywords: engineering design, product competition, address customer needs and develop more competitive products. dynamic network analysis, ERGM, STERGM In this paper, we propose a dynamic network analysis based modeling approach to analyze the evolution of product 1. INTRODUCTION competitions using multi-year product survey data. We choose The objective of this paper is to develop an approach based Separate Temporal Exponential Random Graph Model on dynamic network modeling to study the impact of engineering (STERGM) as the statistical inference framework because it design and existing market competitions on the evolution of considers the evolution of dynamic networks as two separate product competition relations using multi-year product survey processes: formation and dissolution. -

Antecedents of Brand Equity: the Chinese Path to Building Brands a Case-Study of GEELY and BYD Automotive Brands
Durham E-Theses Antecedents of Brand Equity: The Chinese Path to Building Brands A Case-study of GEELY and BYD Automotive Brands MOHAMED, NOHA, AHMED, ALAAELDINE How to cite: MOHAMED, NOHA, AHMED, ALAAELDINE (2013) Antecedents of Brand Equity: The Chinese Path to Building Brands A Case-study of GEELY and BYD Automotive Brands , Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/10670/ Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in Durham E-Theses • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full Durham E-Theses policy for further details. Academic Support Oce, Durham University, University Oce, Old Elvet, Durham DH1 3HP e-mail: [email protected] Tel: +44 0191 334 6107 http://etheses.dur.ac.uk 2 Antecedents of Brand Equity: The Chinese Path to Building Brands A Case-study of GEELY and BYD Automotive Brands Thesis Submitted to Durham University Business School DURHAM UNIVERSITY In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Noha A. Alaa El Dine Mohamed, MBA May 2014 STATEMENT OF COPYRIGHT “The copyright of this thesis rests with the author. -

China Autos and Auto Parts
China autos and auto parts EQUITY: AUTOS & AUTO PARTS New wheels and new drivers Global Markets Research 9 July 2014 Replacement, financing, and favourable seasonality to fuel sales growth upgrade in 2H14F Anchor themes We raise our 2014F PV sales volume growth forecast to 13% from 12% We remain constructive on the Defying market concerns over a slowdown in the beginning of the year, 2H14F outlook for new auto including a real estate market slowdown and more new car sales restrictions, sales, underpinned by growing new passenger vehicle (PV) sales volume grew at 11% YTD, which beats replacement demand and consensus of 8-10% at end-2013. We attribute such resilience to the availability of auto financing. We emergence of replacement demand, auto financing, and rising affordability in prefer SUVs, entry-level luxury, lower-tier cities. As a result, we raise our PV sales volume growth forecast for and OEMs with strong new 2014F and 2015F to 12.9% and 11.4% (from 12.1% and 11.0%), respectively. model pipelines. Any risk of a significant slowdown in 2H14F should be well-contained, owing to these structurally positive factors, as well as further macro policy easing, as Nomura vs consensus projected by the Nomura economics team, in our view. We expect the Street to Our 2014F new PV sales start raising its forecasts around the interim results season in August. volume growth forecast of 13% Key beneficiaries of these positive trends will be SUVs (partly replacement- y-y is above consensus of 10%. demand driven), entry-level luxury models (thanks to rising affordability and availability of auto financing), and OEMs with strong new model pipelines (to Research analysts capture the peak-season demand from September onwards), in our view.