DOCSLIB.ORG

Temperature and Thermodynamics, Part II • Topics to Be Covered

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Temperature and Thermodynamics, Part II • Topics to Be Covered Temperature and Thermodynamics, Part II • Topics to be Covered – Profiles of Temperature in the Boundary Layer – Potential temperature – Adiabatic Lapse Rate – Thermal Stratification 1/8/17 ESPM 129 Biometeorology Why are We Interested in Thermal Stratification of the Atmosphere? • Compare Temperatures measured at Different Heights and Altitudes • Creates or Suppresses Turbulence and Diffusion • Adiabatic Lifting can Cause Cooling – It can cause water to change phases – Condensation Promotes the Formation of Clouds and Rain • Adiabatic Compression can Cause Heating – Downslope Santa Ana winds, Hot and Dry • Microclimate Modification – Wind machines Break the Nocturnal Inversion Layer and Prevent Frost ESPM 129 Biometeorology Changes in Air Pressure and Density with Height, Ideal Conditions 3000 3000 2500 2500 2000 2000 1500 1500 Height, m Height, 1000 m Height, 1000 dP=−ρ g dz mPea ()− a ρ = 500 a 500 RT 0 0 65 70 75 80 85 90 95 100 105 0.85 0.90 0.95 1.00 1.05 1.10 1.15 1.20 Pressure, kPa Air Density, kg m-3 Air Parcel Lifted Expands and Becomes Less Dense because Surrounding Pressure is Less, Consequently Its Temperature Drops as the Parcel Expends ESPM 129 Biometeorology Temperature Profiles in the Boundary Layer: Adiabatic Lapse Rate 3000 2500 −1 2000 Γ=−9.8Kkm 1500 Height, m Height, 1000 500 0 265 270 275 280 285 290 295 300 305 Tair, K ESPM 129 Biometeorology Potential Temperature, θ The Temperature a Parcel of Air would have if it were Expanded or Compressed, Adiabatically, from its Existing Temperature and Pressure to a Standard, near sea level (P=101.3 kPa): Wallace and Hobbs, 1977 P R/(m c ) P R/C θ = T( 0 ) ⋅ p θ = T( 0 ) p P P T, Temperature (K) R, Universal Gas Constant, 8.314 P, Pressure, kPa P0, reference pressure, eg 101.3 kPa Cp, Heat Capacity of air at constant pressure cp, specific heat capacity of air at constant pressure ESPM 129 Biometeorology Temperature Profiles in the Boundary Layer: Adiabatic Lapse Rate and Potential Temperature 70 3000 75 2500 80 2000 85 1500 Height, m Height, 90 1000 Pressure, kPa 95 500 100 0 265 270 275 280 285 290 295 300 305 296 298 300 302 304 T , K air Potential Temperature, K ESPM 129 Biometeorology Profiles of Air and Potential Temperature June 1, 1999, 1800 UT Oak Ridge, TN 700 Virtual Potential Temperature 750 Dry Bulb Temperature 800 Stable 850 Pressure,mb neutral 900 950 unstable 1000 280 290 300 310 320 Temperature, K ESPM 129 Biometeorology Fundamentals of Thermal Stratification stable thermal unstable stratification near neutral thermal stability stratifiation Tparcel < Tair Tparcel > Tair m m m Height, ∂T ∂T Height, Height, =−Γ = −Γ ∂T z ∂z =−Γ ∂ ∂z m m ∂θ Height, ∂θ =0 =0 m ∂θ Height, ∂z ∂z =0 Height, ∂z ESPM 129 Biometeorology Thermal stratification causes the atmosphere to be either buoyant or stable ∂θ ∂T • The atmosphere is neutrally stratified if: v = 0 v = −Γ ∂z ∂z • The atmosphere is unstably stratified if: ∂θ v ∂Tv < 0 < −Γ ∂z ∂z • The atmosphere is stably stratified if: ∂θ v ∂T > 0 v > −Γ ∂z ∂z ESPM 129 Biometeorology Upcoming Features • Describe Adiabatic Processes and Potential Temperature in terms of variables we measure, P and T • Start with 1st Law of Thermodynamics • Normalize 1st Law by Mass, yielding ‘Specific’ Equation • Substitute Terms with Gas Laws, converting Equation from a function of heat capacity for volume, Cv, to that for pressure, Cp • Rearrange Equation so T is on one side and P is on the other • Integrate both sides, yielding equations Ln(T) and Ln(P) • Take anti-log and solve for potential temperature ESPM 129 Biometeorology Adiabatic Process An air parcel changes its physical state (either its pressure, volume or temperature) without heat being added or withdrawn from the surrounding environment . dQ = 0 ESPM 129 Biometeorology Understanding Adiabatic Compression and Expansion, And its Impact on Temperature Profiles With the First Law of Thermodynamics dQ = CV dT + PdV = 0 CV dT = −PdV Change in Change in Work internal Energy No Heat is Exchanged, But Temperature Can Change Change in Internal Energy Equals Change in Work Done on the Parcel ESPM 129 Biometeorology Understanding Adiabatic Processes in the Atmosphere by considering Parcels of Air per unit Mass (m), Specific quantities Q q = Change in Volume per unit Mass is m Equivalent to the change of the inverse in density, ρ W w = m U dV 1 u = = d( ) = dα m m ρ C c = v v m C c = p p m ESPM 129 Biometeorology The Specific Form of the 1st Law of Thermodynamics 1 dq = c dT + Pd( ) = c dT + Pdα v ρ v ESPM 129 Biometeorology Algebraic Tricks to Express dq as f(T, P) and solve for Pdα ρRT RT P = Pα = m m 1 1 d(Pα) = αdP + Pdα = d(RT) = RdT m m R Pdα = −adP + dT m ESPM 129 Biometeorology Algebraic Tricks to Express dq as f(T, P), things we can measure R Pdα = −adP + dT m dq= cv dT− Pdα R dq = (c + )dT −αdP v m ESPM 129 Biometeorology Change in Specific Heat, dq, is a function of the Specific Heat Capacity, cp, times a change in Temperature, minus A change in pressure, dP….terms we can MEASURE R dq=+() c dT −α dP v m R cc=+ pvm dq= cp dT−α dP ESPM 129 Biometeorology Define specific heat capacity at constant P Isobaric case, dP equals 0 R dq = (c + )dT −αdP v m dq R | = c + = c dT p v m p ESPM 129 Biometeorology Adiabatic Process, dq=0 dq==0 cp dT −α dP dP c dT==α dP p ρ ESPM 129 Biometeorology dP mP cdT==α dP ρ = p ρ RT RTdP P: Pressure cp dT = V: volume mP n: number of moles R: Universal Gas Constant m: mass per mole T: absolute air temperature dT R dP ρ: air density c = p TmP ESPM 129 Biometeorology dT R dP R dP == TmcPCP⋅ pp T dT R P dP = ∫ T m c ∫ P θ ⋅ p P0 T R P ln = ln θ m⋅cp P0 ESPM 129 Biometeorology T R P ln = ln θ m⋅cp P0 TRP exp(ln )= exp( ln ) θ mc⋅ p P0 R TPmc⋅ p = θ P0 ESPM 129 Biometeorology Potential Temperature P R/(m c ) θ = T( 0 ) ⋅ p P P R/C θ = T( 0 ) p P ESPM 129 Biometeorology Adiabatic lapse rate, How Temperature Changes with Height 0 =ρ cp dT− dP ρ cp dT= dP dP Hydrostatic Equation = −ρg dz Change in Pressure with height is a function of the density of Air times the acceleration due to gravity, g ESPM 129 Biometeorology Dry Adiabatic Lapse Rate dT dP ρρcg==− p dz dz dT g |adiabatic =−=Γ dz cp The dry adiabatic lapse rate, 9.8 K km-1 ESPM 129 Biometeorology Moist Adiabatic water vapor condenses and latent heat of condensation is released. dT g | =−=Γ dz moistde moist c + λ s p dT λ is the latent heat of vaporization des/dT is the slope of the saturation vapor pressure-temperature curve. ESPM 129 Biometeorology Key Points • Define Thermal Stratification – Neutral, Stable and Unstable Conditions • Define Potential Temperature • Define Adiabatic Processes – Dry and Moist Adiabatic Lapse Rate • Define First Law of Thermodynamics ESPM 129 Biometeorology Summary • Potential temperature is the temperature of a parcel of air that is moved Adiabatically from a level in the atmosphere to a reference Pressure. – It is defined for conditions when changes heat energy are zero (dQ=0). • Thermal stratification causes the ∂θ atmosphere to be either buoyant or v = 0 stable ∂z ∂θ – The atmosphere is neutrally stratified if: v < 0 – The atmosphere is unstably stratified if: ∂z ∂θ – The atmosphere is stably stratified if: v > 0 ∂z ESPM 129 Biometeorology .
Load more

Recommended publications
  • Potential Vorticity
    POTENTIAL VORTICITY Roger K. Smith March 3, 2003 Contents 1 Potential Vorticity Thinking - How might it help the fore- caster? 2 1.1Introduction............................ 2 1.2WhatisPV-thinking?...................... 4 1.3Examplesof‘PV-thinking’.................... 7 1.3.1 A thought-experiment for understanding tropical cy- clonemotion........................ 7 1.3.2 Kelvin-Helmholtz shear instability . ......... 9 1.3.3 Rossby wave propagation in a β-planechannel..... 12 1.4ThestructureofEPVintheatmosphere............ 13 1.4.1 Isentropicpotentialvorticitymaps........... 14 1.4.2 The vertical structure of upper-air PV anomalies . 18 2 A Potential Vorticity view of cyclogenesis 21 2.1PreliminaryIdeas......................... 21 2.2SurfacelayersofPV....................... 21 2.3Potentialvorticitygradientwaves................ 23 2.4 Baroclinic Instability . .................... 28 2.5 Applications to understanding cyclogenesis . ......... 30 3 Invertibility, iso-PV charts, diabatic and frictional effects. 33 3.1 Invertibility of EPV ........................ 33 3.2Iso-PVcharts........................... 33 3.3Diabaticandfrictionaleffects.................. 34 3.4Theeffectsofdiabaticheatingoncyclogenesis......... 36 3.5Thedemiseofcutofflowsandblockinganticyclones...... 36 3.6AdvantageofPVanalysisofcutofflows............. 37 3.7ThePVstructureoftropicalcyclones.............. 37 1 Chapter 1 Potential Vorticity Thinking - How might it help the forecaster? 1.1 Introduction A review paper on the applications of Potential Vorticity (PV-) concepts by Brian
    [Show full text]
  • Chapter 2 Approximate Thermodynamics
    Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR.
    [Show full text]
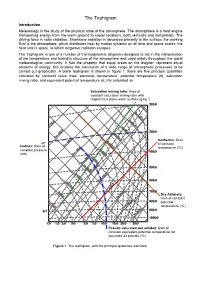
  • The Tephigram Introduction Meteorology Is the Study of the Physical State of the Atmosphere
    The Tephigram Introduction Meteorology is the study of the physical state of the atmosphere. The atmosphere is a heat engine transporting energy from the warm ground to cooler locations, both vertically and horizontally. The driving force is solar radiation. Shortwave radiation is absorbed primarily at the surface; the working fluid is the atmosphere, which distributes heat by motion systems on all time and space scales; the heat sink is space, to which longwave radiation escapes. The Tephigram is one of a number of thermodynamic diagrams designed to aid in the interpretation of the temperature and humidity structure of the atmosphere and used widely throughout the world meteorological community. It has the property that equal areas on the diagram represent equal amounts of energy; this enables the calculation of a wide range of atmospheric processes to be carried out graphically. A blank tephigram is shown in figure 1; there are five principal quantities indicated by constant value lines: pressure, temperature, potential temperature (θ), saturation mixing ratio, and equivalent potential temperature (θe) for saturated air. Saturation mixing ratio: lines of constant saturation mixing ratio with respect to a plane water surface (g kg-1) Isotherms: lines of constant Isobars: lines of temperature (ºC) constant pressure (mb) Dry Adiabats: lines of constant potential temperature (ºC) Pseudo saturated wet adiabat: lines of constant equivalent potential temperature for saturated air parcels (ºC) Figure 1. The tephigram, with the principal quantities indicated. The principal axes of a tephigram are temperature and potential temperature; these are straight and perpendicular to each other, but rotated through about 45º anticlockwise so that lines of constant temperature run from bottom left to top right on the diagram.
    [Show full text]
  • Dry Adiabatic Temperature Lapse Rate
    ATMO 551a Fall 2010 Dry Adiabatic Temperature Lapse Rate As we discussed earlier in this class, a key feature of thick atmospheres (where thick means atmospheres with pressures greater than 100-200 mb) is temperature decreases with increasing altitude at higher pressures defining the troposphere of these planets. We want to understand why tropospheric temperatures systematically decrease with altitude and what the rate of decrease is. The first order explanation is the dry adiabatic lapse rate. An adiabatic process means no heat is exchanged in the process. For this to be the case, the process must be “fast” so that no heat is exchanged with the environment. So in the first law of thermodynamics, we can anticipate that we will set the dQ term equal to zero. To get at the rate at which temperature decreases with altitude in the troposphere, we need to introduce some atmospheric relation that defines a dependence on altitude. This relation is the hydrostatic relation we have discussed previously. In summary, the adiabatic lapse rate will emerge from combining the hydrostatic relation and the first law of thermodynamics with the heat transfer term, dQ, set to zero. The gravity side The hydrostatic relation is dP = −g ρ dz (1) which relates pressure to altitude. We rearrange this as dP −g dz = = α dP (2) € ρ where α = 1/ρ is known as the specific volume which is the volume per unit mass. This is the equation we will use in a moment in deriving the adiabatic lapse rate. Notice that € F dW dE g dz ≡ dΦ = g dz = g = g (3) m m m where Φ is known as the geopotential, Fg is the force of gravity and dWg is the work done by gravity.
    [Show full text]
  • Introduction to Atmospheric Dynamics Chapter 2
    Introduction to Atmospheric Dynamics Chapter 2 Paul A. Ullrich [email protected] Part 3: Buoyancy and Convection Vertical Structure This cooling with height is related to the dynamics of the atmosphere. The change of temperature with height is called the lapse rate. Defnition: The lapse rate is defned as the rate (for instance in K/km) at which temperature decreases with height. @T Γ ⌘@z Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate For a dry adiabatic, stable, hydrostatic atmosphere the potential temperature θ does not vary in the vertical direction: @✓ =0 @z In a dry adiabatic, hydrostatic atmosphere the temperature T must decrease with height. How quickly does the temperature decrease? R/cp p0 Note: Use ✓ = T p ✓ ◆ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate The adiabac change in temperature with height is T @✓ @T g = + ✓ @z @z cp For dry adiabac, hydrostac atmosphere: @T g = Γd − @z cp ⌘ Defnition: The dry adiabatic lapse rate is defned as the g rate (for instance in K/km) at which the temperature of an Γd air parcel will decrease with height if raised adiabatically. ⌘ cp g 1 9.8Kkm− cp ⇡ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate This profle should be very close to the adiabatic lapse rate in a dry atmosphere. Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Fundamentals Even in adiabatic motion, with no external source of heating, if a parcel moves up or down its temperature will change. • What if a parcel moves about a surface of constant pressure? • What if a parcel moves about a surface of constant height? If the atmosphere is in adiabatic balance, the temperature still changes with height.
    [Show full text]
  • Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity
    APRIL 2016 Y U V A L A N D K A S P I 1709 Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity JANNI YUVAL AND YOHAI KASPI Department of Earth and Planetary Sciences, Weizmann Institute of Science, Rehovot, Israel (Manuscript received 12 May 2015, in final form 25 October 2015) ABSTRACT The relation between the mean meridional temperature gradient and eddy fluxes has been addressed by several eddy flux closure theories. However, these theories give little information on the dependence of eddy fluxes on the vertical structure of the temperature gradient. The response of eddies to changes in the vertical structure of the temperature gradient is especially interesting since global circulation models suggest that as a result of greenhouse warming, the lower-tropospheric temperature gradient will decrease whereas the upper- tropospheric temperature gradient will increase. The effects of the vertical structure of baroclinicity on at- mospheric circulation, particularly on the eddy activity, are investigated. An idealized global circulation model with a modified Newtonian relaxation scheme is used. The scheme allows the authors to obtain a heating profile that produces a predetermined mean temperature profile and to study the response of eddy activity to changes in the vertical structure of baroclinicity. The results indicate that eddy activity is more sensitive to temperature gradient changes in the upper troposphere. It is suggested that the larger eddy sensitivity to the upper-tropospheric temperature gradient is a consequence of large baroclinicity concen- trated in upper levels. This result is consistent with a 1D Eady-like model with nonuniform shear showing more sensitivity to shear changes in regions of larger baroclinicity.
    [Show full text]
  • Nomaly Patterns in the Near-Surface Baroclinicity And
    1 Dominant Anomaly Patterns in the Near-Surface Baroclinicity and 2 Accompanying Anomalies in the Atmosphere and Oceans. Part II: North 3 Pacific Basin ∗ † 4 Mototaka Nakamura and Shozo Yamane 5 Japan Agency for Marine-Earth Science and Technology, Yokohama, Kanagawa, Japan ∗ 6 Corresponding author address: Mototaka Nakamura, Japan Agency for Marine-Earth Science and 7 Technology, 3173-25 Showa-machi, Kanazawa-ku, Yokohama, Kanagawa 236-0001, Japan. 8 E-mail: [email protected] † 9 Current affiliation: Science and Engineering, Doshisha University, Kyotanabe, Kyoto, Japan. Generated using v4.3.2 of the AMS LATEX template 1 ABSTRACT 10 Variability in the monthly-mean flow and storm track in the North Pacific 11 basin is examined with a focus on the near-surface baroclinicity. Dominant 12 patterns of anomalous near-surface baroclinicity found from EOF analyses 13 generally show mixed patterns of shift and changes in the strength of near- 14 surface baroclinicity. Composited anomalies in the monthly-mean wind at 15 various pressure levels based on the signals in the EOFs show accompany- 16 ing anomalies in the mean flow up to 50 hPa in the winter and up to 100 17 hPa in other seasons. Anomalous eddy fields accompanying the anomalous 18 near-surface baroclinicity patterns exhibit, broadly speaking, structures antic- 19 ipated from simple linear theories of baroclinic instability, and suggest a ten- 20 dency for anomalous wave fluxes to accelerate–decelerate the surface west- 21 erly accordingly. However, the relationship between anomalous eddy fields 22 and anomalous near-surface baroclinicity in the midwinter is not consistent 23 with the simple linear baroclinic instability theories.
    [Show full text]
  • Thermodynamics of Convection in the Moist Atmosphere B
    Thermodynamics of convection in the moist atmosphere B. Legras, LMD/ENS http://www.lmd.ens.fr/legras 1 References recommanded books: - Fundamentals of Atmospheric Physics, M.L. Salby, Academic Press - Cloud dynamics, R.A. Houze, Academic Press Other more advanced books (plus avancés): - Thermodynamics of Atmospheres and Oceans, J.A. Curry & P.J. Webster - Atmospheric Convection, K.A. Emanuel, Oxford Univ. Press Papers - Bolton, The computation of equivalent potential temperature, MWR, 108, 1046- 1053, 1980 2 OUTLINE OF FIRST PART ● Introduction. Distribution of clouds and atmospheric circulation ● Atmospheric stratification. Dry air thermodynamics and stability. ● Moist unsaturated thermodynamics. Virtual temperature. Boundary layer. ● Moist air thermodynamics and the generation of clouds. ● Equivalent potential temperature and potential instability. ● Pseudo-equivalent potential temperature and conditional instability ● CAPE, CIN and ● An example of large-scale cloud parameterization ● 3 Introduction. Distribution of clouds and atmospheric circulation 4 Large-scale organisation of clouds IR false color composite image, obtained par combined data from 5 Geostationary satellites 22/09/2005 18:00TU (GOES-10 (135O), GOES-12 (75O), METEOSAT-7 (OE), METEOSAT-5 (63E), MTSAT (140E)) Cloud bands Cloud bands Cyclone Rita Clusters of convective clouds associated with mid- Cyclone Rita Clusters of convective clouds associated with mid- in the tropical region (15S – latitude in the tropical region (15S – latitude 15 N) perturbations 15 N) perturbations
    [Show full text]
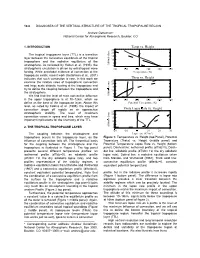
  • Temp Vs. Height Theta Vs. Height Theta Lapse Rate Vs. Height
    10.8 DIAGNOSES OF THE VERTICAL STRUCTURE OF THE TROPICAL TROPOPAUSE REGION Andrew Gettelman* National Center for Atmospheric Research, Boulder, CO 1. INTRODUCTION Temp vs. Height 25 20 The tropical tropopause layer (TTL) is a transition 15 layer between the convective equilibrium of the tropical ¦ 10 troposphere and the radiative equilibrium of the 5 stratosphere. As reviewed by Holton et al. (1995), the Altitude (km) 0 ¢ ¡ ¢ ¡ ¢ stratospheric circulation is driven by extratropical wave 100¡ 150 200 250 300 350 o forcing. While anectodal evidence of convection at the Temperature£¥¤ ( K) tropopause exists, recent work (Gettelman et al., 2001) indicates that such convection is rare. In this work we Theta vs. Height 25 examine the relative roles of tropospheric convection 20 and large scale diabatic heating at the tropopause and 15 ¦ try to define the coupling between the troposphere and 10 the stratosphere. 5 We find that the level of main convective influence Altitude (km) 0 ¡ ¡ ¡ ¡ ¡ in the upper troposphere is at 10−12km, which we 200¡ 300 400 500 600 700 define as the base of the tropopause layer. Above this Potential Temeprature (K) level, as noted by Folkins et al. (1999), the impact of convection drops off rapidly as air approaches Theta Lapse § Rate vs. Height 25 stratospheric stability. The level of maximum 20 convection varies in space and time, which may have 15 ¦ important implications for the chemistry of the TTL. 10 5 2. THE TROPICAL TROPOPAUSE LAYER Altitude (km) 0 © ¡ -20¨ -10 0 10 20 30 -1 The coupling between the stratosphere and Lapse rate (K km ) troposphere occurs in the tropopause layer, as the Figure 1: Temperature vs.
    [Show full text]
  • References: Humidity Variables
    ESCI 340 - Cloud Physics and Precipitation Processes Lesson 2 - Thermodynamics of Moist Air Dr. DeCaria References: Glossary of Meteorology, 2nd ed., American Meteorological Society A Short Course in Cloud Physics, 3rd ed., Rogers and Yau, Chs. 1 and 2 Humidity Variables This section contains a review of the humidity variables used by meteorologists. vapor pressure, e: The partial pressure of the water vapor in the atmosphere. saturation vapor pressure, es: The vapor pressure at which liquid water and vapor would be in equilibrium. • Saturation vapor pressure is found from the Clausius-Clapeyron Equation, Lv 1 1 es = e0 exp − (1) Rv T0 T where T0 = 273:15K, e0 = 611 Pa, Lv is the latent heat of vaporization, and Rv is the specific gas constant for water vapor. • The Clausius-Clapeyron equation gives the saturation vapor pressure over a flat surface of pure liquid water. • If the liquid contains impurities, or the interface between the liquid and vapor is curved, corrections for the solute effect and curvature effect must be applied. Relative Humidity, RH: Relative humidity is defined as the ratio of vapor pressure to saturation vapor pressure, and is expressed as a percent. e RH = × 100% (2) es • Relative humidity is always defined in terms of a flat surface of pure liquid water. • The World Meteorological Organization (WMO) uses an alternate definition of relative humidity, which is the ratio of mixing ratio to saturation mixing ratio, r RH = × 100%: (3) rs The two definitions (2) and (3) are not identical, but are very close and are usually considered to be interchangeable.
    [Show full text]
  • Potential Temperature Manuel Baumgartner1,2, Ralf Weigel2, Ulrich Achatz4, Allan H
    https://doi.org/10.5194/acp-2020-361 Preprint. Discussion started: 4 May 2020 c Author(s) 2020. CC BY 4.0 License. Reappraising the appropriate calculation of a common meteorological quantity: Potential Temperature Manuel Baumgartner1,2, Ralf Weigel2, Ulrich Achatz4, Allan H. Harvey3, and Peter Spichtinger2 1Zentrum für Datenverarbeitung, Johannes Gutenberg University Mainz, Germany 2Institute for Atmospheric Physics, Johannes Gutenberg University Mainz, Germany 3Applied Chemicals and Materials Division, National Institute of Standards and Technology, Boulder, CO, USA 4Institut für Atmosphäre und Umwelt, Goethe-Universität Frankfurt, Frankfurt am Main, Germany Correspondence: Manuel Baumgartner ([email protected]) Abstract. The potential temperature is a widely used quantity in atmospheric science since it is conserved for air’s adiabatic changes of state. Its definition involves the specific heat capacity of dry air, which is traditionally assumed as constant. However, the literature provides different values of this allegedly constant parameter, which are reviewed and discussed in this study. Furthermore, we derive the potential temperature for a temperature-dependent parameterization of the specific heat capacity of 5 dry air, thus providing a new reference potential temperature with a more rigorous basis. This new reference shows different values and vertical gradients in the upper troposphere and the stratosphere compared to the potential temperature that assumes constant heat capacity. The application of the new reference potential temperature to the prediction of gravity wave breaking altitudes reveals that the predicted wave breaking height may depend on the definition of the potential temperature used. 1 Introduction 10 According to the book Thermodynamics of the Atmosphere by Alfred Wegener (1911), the first published use of the expression potential temperature in meteorology is credited to Wladimir Köppen (1888)1 and Wilhelm von Bezold (1888), both following the conclusions of Hermann von Helmholtz (1888) (Kutzbach, 2016).
    [Show full text]
  • An Assessment of Low-Level Baroclinity and Vorticity Within a Simulated Supercell
    FEBRUARY 2013 BECK AND WEISS 649 An Assessment of Low-Level Baroclinity and Vorticity within a Simulated Supercell JEFFREY BECK Centre National de Recherches Me´te´orologiques, Me´te´o-France, Toulouse, France CHRISTOPHER WEISS Atmospheric Science Group, Texas Tech University, Lubbock, Texas (Manuscript received 7 May 2011, in final form 12 July 2012) ABSTRACT Idealized supercell modeling has provided a wealth of information regarding the evolution and dynamics within supercell thunderstorms. However, discrepancies in conceptual models exist, including uncertainty regarding the existence, placement, and forcing of low-level boundaries in these storms, as well as their importance in low-level vorticity development. This study offers analysis of the origins of low-level bound- aries and vertical vorticity within the low-level mesocyclone of a simulated supercell. Low-level boundary location shares similarities with previous modeling studies; however, the development and evolution of these boundaries differ from previous conceptual models. The rear-flank gust front develops first, whereas the formation of a boundary extending north of the mesocyclone undergoes numerous iterations caused by competing outflow and inflow before a steady-state boundary is produced. A third boundary extending northeast of the mesocyclone is produced through evaporative cooling of inflow air and develops last. Con- ceptual models for the simulation were created to demonstrate the evolution and structure of the low-level boundaries. Only the rear-flank gust front may be classified as a ‘‘gust front,’’ defined as having a strong wind shift, delineation between inflow and outflow air, and a strong pressure gradient across the boundary. Trajectory analyses show that parcels traversing the boundary north of the mesocyclone and the rear-flank gust front play a strong role in the development of vertical vorticity existing within the low-level mesocyclone.
    [Show full text]