Potential Vorticity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Potential Vorticity Dynamics and Tropopause Fold
POTENTIAL VORTICITY DYNAMICS AND TROPOPAUSE FOLD M.D. ANDREI1,2, M. PIETRISI1,2, S. STEFAN1 1 University of Bucharest, Faculty of Physics, P.O.BOX MG 11, Magurele, Bucharest, Romania Emails: [email protected]; [email protected] 2 National Meteorological Administration, Bucuresti-Ploiesti Ave., No. 97, 013686, Bucharest, Romania Received November 1, 2017 Abstract. Extra tropical cyclones evolution depends a lot on the dynamically and thermodynamically interactions between the lower and the upper troposphere. The aim of this paper is to demonstrate the importance of dynamic tropopause fold in the development of a cyclone which affected Romania in 12th and 13th of November, 2016. The coupling between a positive potential vorticity anomaly and the jet stream has caused the fall of dynamic tropopause, which has a great influence in the cyclone deepening. This synoptic situation has resulted in a big amount of precipitation and strong wind gusts. For the study, ALARO limited area spectral model analyzes (e.g., 300 hPa Potential Vorticity, 1,5 PVU field height, 300 hPa winds, mean sea level pressure), data from the Romanian National Meteorological Administration meteorological stations, cross-sections and satellite images (water vapor and RGB) were used. Accordingly, the results of this study will be used in operational forecast, for similar situations which would appear in the future, and can improve it. Key words: potential vorticity, tropopause fold, cyclone. 1. INTRODUCTION Dynamic tropopause is the 1.5 or 2 PVU (potential vorticity units) surface that separates the dry, stable, stratospheric air from the humid, unstable, tropospheric air [1]. The dynamic tropopause fold corresponds to a positive potential vorticity anomaly, with high amplitude in the upper troposphere [2, 3], which induces a cyclonic circulation that propagates to the surface and reduce, under it, static stability. -

Potential Vorticity Diagnosis of a Simulated Hurricane. Part I: Formulation and Quasi-Balanced Flow
1JULY 2003 WANG AND ZHANG 1593 Potential Vorticity Diagnosis of a Simulated Hurricane. Part I: Formulation and Quasi-Balanced Flow XINGBAO WANG AND DA-LIN ZHANG Department of Meteorology, University of Maryland at College Park, College Park, Maryland (Manuscript received 20 August 2002, in ®nal form 27 January 2003) ABSTRACT Because of the lack of three-dimensional (3D) high-resolution data and the existence of highly nonelliptic ¯ows, few studies have been conducted to investigate the inner-core quasi-balanced characteristics of hurricanes. In this study, a potential vorticity (PV) inversion system is developed, which includes the nonconservative processes of friction, diabatic heating, and water loading. It requires hurricane ¯ows to be statically and inertially stable but allows for the presence of small negative PV. To facilitate the PV inversion with the nonlinear balance (NLB) equation, hurricane ¯ows are decomposed into an axisymmetric, gradient-balanced reference state and asymmetric perturbations. Meanwhile, the nonellipticity of the NLB equation is circumvented by multiplying a small parameter « and combining it with the PV equation, which effectively reduces the in¯uence of anticyclonic vorticity. A quasi-balanced v equation in pseudoheight coordinates is derived, which includes the effects of friction and diabatic heating as well as differential vorticity advection and the Laplacians of thermal advection by both nondivergent and divergent winds. This quasi-balanced PV±v inversion system is tested with an explicit simulation of Hurricane Andrew (1992) with the ®nest grid size of 6 km. It is shown that (a) the PV±v inversion system could recover almost all typical features in a hurricane, and (b) a sizeable portion of the 3D hurricane ¯ows are quasi-balanced, such as the intense rotational winds, organized eyewall updrafts and subsidence in the eye, cyclonic in¯ow in the boundary layer, and upper-level anticyclonic out¯ow. -

(Potential) Vorticity: the Swirling Motion of Geophysical Fluids
(Potential) vorticity: the swirling motion of geophysical fluids Vortices occur abundantly in both atmosphere and oceans and on all scales. The leaves, chasing each other in autumn, are driven by vortices. The wake of boats and brides form strings of vortices in the water. On the global scale we all know the rotating nature of tropical cyclones and depressions in the atmosphere, and the gyres constituting the large-scale wind driven ocean circulation. To understand the role of vortices in geophysical fluids, vorticity and, in particular, potential vorticity are key quantities of the flow. In a 3D flow, vorticity is a 3D vector field with as complicated dynamics as the flow itself. In this lecture, we focus on 2D flow, so that vorticity reduces to a scalar field. More importantly, after including Earth rotation a fairly simple equation for planar geostrophic fluids arises which can explain many characteristics of the atmosphere and ocean circulation. In the lecture, we first will derive the vorticity equation and discuss the various terms. Next, we define the various vorticity related quantities: relative, planetary, absolute and potential vorticity. Using the shallow water equations, we derive the potential vorticity equation. In the final part of the lecture we discuss several applications of this equation of geophysical vortices and geophysical flow. The preparation material includes - Lecture slides - Chapter 12 of Stewart (http://www.colorado.edu/oclab/sites/default/files/attached- files/stewart_textbook.pdf), of which only sections 12.1-12.3 are discussed today. Willem Jan van de Berg Chapter 12 Vorticity in the Ocean Most of the fluid flows with which we are familiar, from bathtubs to swimming pools, are not rotating, or they are rotating so slowly that rotation is not im- portant except maybe at the drain of a bathtub as water is let out. -

Statistical Single-Station Short-Term Forecasting of Temperature and Probability of Precipitation: Area Interpolation and NWP Combination
APRIL 1999 RAIBLE ET AL. 203 Statistical Single-Station Short-Term Forecasting of Temperature and Probability of Precipitation: Area Interpolation and NWP Combination CHRISTOPH C. RAIBLE,GEORG BISCHOF,KLAUS FRAEDRICH, AND EDILBERT KIRK Meteorologisches Institut, UniversitaÈt Hamburg, Hamburg, Germany (Manuscript received 18 February 1998, in ®nal form 21 October 1998) ABSTRACT Two statistical single-station short-term forecast schemes are introduced and applied to real-time weather prediction. A multiple regression model (R model) predicting the temperature anomaly and a multiple regression Markov model (M model) forecasting the probability of precipitation are shown. The following forecast ex- periments conducted for central European weather stations are analyzed: (a) The single-station performance of the statistical models, (b) a linear error minimizing combination of independent forecasts of numerical weather prediction and statistical models, and (c) the forecast representation for a region deduced by applying a suitable interpolation technique. This leads to an operational weather forecasting system for the temperature anomaly and the probability of precipitation; the statistical techniques demonstrated provide a potential for future ap- plications in operational weather forecasts. 1. Introduction (Wilson 1985; Dallavalle 1996; KnuÈpffer 1996) as well Although, in general, numerical weather prediction as the long-term prediction (more than a month ahead) (NWP) models are hard to beat in very short-term fore- of monthly mean temperature (Nicholls 1980; Navato casting (up to 24 h), they do require a substantial amount 1981; Madden 1981; Norton 1985). Thus, the ®rst pur- of computation time and the model forecasts are not pose of this paper is to set up a statistical model of always stable at this timescale. -

ISSUES : DATA SET Investigating the Footprint of Climate Change On
- 1 - TIEE Teaching Issues and Experiments in Ecology - Volume 10, April 2014 ISSUES : DATA SET Investigating the footprint of climate change on phenology and ecological interactions in north-central North America Kellen M. Calinger Department of Evolution, Ecology, and Organismal Biology, The Ohio State University, Columbus, OH 43210-1293; [email protected] THE ECOLOGICAL QUESTION: Have long-term temperatures changed throughout Ohio? How will these temperature changes impact plant and animal phenology, ecological interactions, and, as a result, species diversity? ECOLOGICAL CONTENT: Climate change, phenology, pollinators, trophic mismatch, species diversity, arrival time, mutualism WHAT STUDENTS DO: o Produce and analyze graphs of temperature change using large, long-term data sets (Synthesis, Analysis) o Develop methods for calculating species-specific shifts in flowering time with temperature increase (Synthesis) o Use these methods to calculate flowering shifts in six plant Aquilegia canadensis (red columbine) species (Application) flowering with open and closed flowers o Describe the ecological consequences of shifting plant and animal phenology (Comprehension) o Understand how interactions between species as well as with their abiotic environment affect community structure and species diversity (Knowledge, Comprehension) o Evaluate data “cherry-picking” as a climate change skeptic tactic (Evaluation) STUDENT-ACTIVE APPROACHES: Open-ended inquiry, guided inquiry, cooperative learning, critical thinking SKILLS: Work with large data sets, create and analyze multiple types of graphs, connect the development of procedures and data analysis to clarifying ecological impacts of climate change ASSESSABLE OUTCOMES: Student-made graphs, calculations of temperature and phenology shifts, answers to short questions, brief paragraphs describing student-generated methods TIEE, Volume 10 © 2014 – Kellen M. -

A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods
water Review A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods Elahe Akbari 1,2, Seyed Kazem Alavipanah 1,*, Mehrdad Jeihouni 1, Mohammad Hajeb 1,3, Dagmar Haase 4,5 and Sadroddin Alavipanah 4 1 Department of Remote Sensing and GIS, Faculty of Geography, University of Tehran, Tehran 1417853933, Iran; [email protected] (E.A.); [email protected] (M.J.); [email protected] (M.H.) 2 Department of Climatology and Geomorphology, Faculty of Geography and Environmental Sciences, Hakim Sabzevari University, Sabzevar 9617976487, Iran 3 Department of Remote Sensing and GIS, Shahid Beheshti University, Tehran 1983963113, Iran 4 Department of Geography, Humboldt University of Berlin, Unter den Linden 6, 10099 Berlin, Germany; [email protected] (D.H.); [email protected] (S.A.) 5 Department of Computational Landscape Ecology, Helmholtz Centre for Environmental Research UFZ, 04318 Leipzig, Germany * Correspondence: [email protected]; Tel.: +98-21-6111-3536 Received: 3 October 2017; Accepted: 16 November 2017; Published: 14 December 2017 Abstract: Oceans/Seas are important components of Earth that are affected by global warming and climate change. Recent studies have indicated that the deeper oceans are responsible for climate variability by changing the Earth’s ecosystem; therefore, assessing them has become more important. Remote sensing can provide sea surface data at high spatial/temporal resolution and with large spatial coverage, which allows for remarkable discoveries in the ocean sciences. The deep layers of the ocean/sea, however, cannot be directly detected by satellite remote sensors. -

Appendix a Gempak Parameters
GEMPAK Parameters APPENDIX A GEMPAK PARAMETERS This appendix contains a list of the GEMPAK parameters. Algorithms used in computing these parameters are also included. The following constants are used in the computations: KAPPA = Poisson's constant = 2 / 7 G = Gravitational constant = 9.80616 m/sec/sec GAMUSD = Standard atmospheric lapse rate = 6.5 K/km RDGAS = Gas constant for dry air = 287.04 J/K/kg PI = Circumference / diameter = 3.14159265 References for some of the algorithms: Bolton, D., 1980: The computation of equivalent potential temperature., Monthly Weather Review, 108, pp 1046-1053. Miller, R.C., 1972: Notes on Severe Storm Forecasting Procedures of the Air Force Global Weather Central, AWS Tech. Report 200. Wallace, J.M., P.V. Hobbs, 1977: Atmospheric Science, Academic Press, 467 pp. TEMPERATURE PARAMETERS TMPC - Temperature in Celsius TMPF - Temperature in Fahrenheit TMPK - Temperature in Kelvin STHA - Surface potential temperature in Kelvin STHK - Surface potential temperature in Kelvin N-AWIPS 5.6.L User’s Guide A-1 October 2003 GEMPAK Parameters STHC - Surface potential temperature in Celsius STHE - Surface equivalent potential temperature in Kelvin STHS - Surface saturation equivalent pot. temperature in Kelvin THTA - Potential temperature in Kelvin THTK - Potential temperature in Kelvin THTC - Potential temperature in Celsius THTE - Equivalent potential temperature in Kelvin THTS - Saturation equivalent pot. temperature in Kelvin TVRK - Virtual temperature in Kelvin TVRC - Virtual temperature in Celsius TVRF - Virtual -

Genesis of Diamond Dust and Thick Cloud Episodes Observed Above Dome C, Antarctica by Ricaud Et Al
Manuscript Title: Genesis of Diamond Dust and Thick Cloud Episodes observed above Dome C, Antarctica by Ricaud et al. RESPONSES TO THE REVIEWERS We would like to thank the reviewers for their insightful comments that were helpful in improving substantially the presentation and contents of the revised manuscript. We have addressed appropriately all issues raised by the reviewers. The reviewers' comments are repeated below in blue and our responses appear in black. The title has been modified into: Genesis of Diamond Dust, Ice Fog and Thick Cloud Episodes observed and modelled above Dome C, Antarctica We have inserted this sentence in the acknowledgments: We finally would like to thank the two anonymous reviewers to their fruitful comments. Changes have been highlighted in yellow in the revised manuscript. 1 Anonymous Referee #1 This manuscript intends to study of cold weather conditions (over Antarctica). It focuses on clouds and diamond dust, and various observational platforms and model simulations over more than 1 month of observations. There are several issues with this manuscript and need to be improved significantly before goes to publication. Because of above I see that paper needs to be improved significantly before making a decision if it is appropriate for this ACP. ® Specific changes have been made in response to the reviewers' comments and are described below. Major/minor issues: 1. Objectives are not clearly set up. Lots of information but nothing to do with objectives. ® We have clarified this crucial point. The objectives of the paper are mainly to investigate the processes that cause the presence of thick cloud and diamond dust/ice fog episodes above the Dome C station based on observations and verify whether operational models can evaluate them. -

Predicting Extremes Presenter: Gil Compo
Predicting Extremes Presenter: Gil Compo Subject Matter Experts: Tom Hamill, Marty Hoerling, Matt Newman, Judith Perlwitz NOAA Physical Sciences Laboratory Review November 16-20, 2020 Physical Science for Predicting Extremes Observe Initial focus in What extreme events have happened? How can we measure the important processes? Predicting Extremes is on Users & Stakeholders Subseasonal to Understand Seasonal (S2S) Physical Sciences LaboratoryHow predictable is an extreme event? What are the physical laws governing the processes? Predict Generate improved predictions, consistent with our understanding of the physical laws. By design, PSL’s activities are “predicting Predict the expected forecast skill in advance the nation’s path through a varying and changing climate” consistent with NOAA’s encompassing mission to “understand Communicate and predict changes in climate, weather, Convey what is known and not known about extremes in oceans, and coasts, and to share that ways that facilitate effective decision making. knowledge and information with others.” 2 Goals for Predicting Extremes • Observe Extreme Events Advanced observations Data assimilation Reanalysis • Understand conditional and unconditional (climatological) distributions and their tails What is predictable at what leads? • Improve predictions of these distributions at all leads Even the mean is hard! Only some forecasts may have useful skill – Need to identify “Forecasts of Opportunity” • Communicate new understanding and improved predictions to stakeholders and decision makers -

Chapter 2 Approximate Thermodynamics
Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR. -
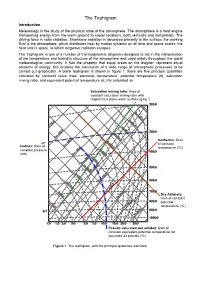
The Tephigram Introduction Meteorology Is the Study of the Physical State of the Atmosphere
The Tephigram Introduction Meteorology is the study of the physical state of the atmosphere. The atmosphere is a heat engine transporting energy from the warm ground to cooler locations, both vertically and horizontally. The driving force is solar radiation. Shortwave radiation is absorbed primarily at the surface; the working fluid is the atmosphere, which distributes heat by motion systems on all time and space scales; the heat sink is space, to which longwave radiation escapes. The Tephigram is one of a number of thermodynamic diagrams designed to aid in the interpretation of the temperature and humidity structure of the atmosphere and used widely throughout the world meteorological community. It has the property that equal areas on the diagram represent equal amounts of energy; this enables the calculation of a wide range of atmospheric processes to be carried out graphically. A blank tephigram is shown in figure 1; there are five principal quantities indicated by constant value lines: pressure, temperature, potential temperature (θ), saturation mixing ratio, and equivalent potential temperature (θe) for saturated air. Saturation mixing ratio: lines of constant saturation mixing ratio with respect to a plane water surface (g kg-1) Isotherms: lines of constant Isobars: lines of temperature (ºC) constant pressure (mb) Dry Adiabats: lines of constant potential temperature (ºC) Pseudo saturated wet adiabat: lines of constant equivalent potential temperature for saturated air parcels (ºC) Figure 1. The tephigram, with the principal quantities indicated. The principal axes of a tephigram are temperature and potential temperature; these are straight and perpendicular to each other, but rotated through about 45º anticlockwise so that lines of constant temperature run from bottom left to top right on the diagram. -

A Vorticity-And-Stability Diagram As a Means to Study Potential Vorticity
https://doi.org/10.5194/wcd-2021-31 Preprint. Discussion started: 29 June 2021 c Author(s) 2021. CC BY 4.0 License. A vorticity-and-stability diagram as a means to study potential vorticity nonconservation Gabriel Vollenweider1, Elisa Spreitzer1, and Sebastian Schemm1 1Institute for Atmospheric and Climate Science, ETH Zürich, Zürich, Switzerland Correspondence: Sebastian Schemm ([email protected]) Abstract. The study of atmospheric circulation from a potential vorticity (PV) perspective has advanced our mechanistic understanding of the development and propagation of weather systems. The formation of PV anomalies by nonconservative processes can provide additional insight into the diabatic-to-adiabatic coupling in the atmosphere. PV nonconservation can be driven by changes in static stability, vorticity or a combination of both. For example, in the presence of localized latent heating, 5 the static stability increases below the level of maximum heating and decreases above this level. However, the vorticity changes in response to the changes in static stability (and vice versa), making it difficult to disentangle stability from vorticity-driven PV changes. Further diabatic processes, such as friction or turbulent momentum mixing, result in momentum-driven, and hence vorticity-driven, PV changes in the absence of moist diabatic processes. In this study, a vorticity-and-stability diagram is introduced as a means to study and identify periods of stability- and vorticity-driven changes in PV. Potential insights and 10 limitations from such a hyperbolic diagram are investigated based on three case studies. The first case is an idealized warm conveyor belt (WCB) in a baroclinic channel simulation. The simulation allows only condensation and evaporation.