DOCSLIB.ORG

An Assessment of Low-Level Baroclinity and Vorticity Within a Simulated Supercell

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
An Assessment of Low-Level Baroclinity and Vorticity Within a Simulated Supercell FEBRUARY 2013 BECK AND WEISS 649 An Assessment of Low-Level Baroclinity and Vorticity within a Simulated Supercell JEFFREY BECK Centre National de Recherches Me´te´orologiques, Me´te´o-France, Toulouse, France CHRISTOPHER WEISS Atmospheric Science Group, Texas Tech University, Lubbock, Texas (Manuscript received 7 May 2011, in final form 12 July 2012) ABSTRACT Idealized supercell modeling has provided a wealth of information regarding the evolution and dynamics within supercell thunderstorms. However, discrepancies in conceptual models exist, including uncertainty regarding the existence, placement, and forcing of low-level boundaries in these storms, as well as their importance in low-level vorticity development. This study offers analysis of the origins of low-level bound- aries and vertical vorticity within the low-level mesocyclone of a simulated supercell. Low-level boundary location shares similarities with previous modeling studies; however, the development and evolution of these boundaries differ from previous conceptual models. The rear-flank gust front develops first, whereas the formation of a boundary extending north of the mesocyclone undergoes numerous iterations caused by competing outflow and inflow before a steady-state boundary is produced. A third boundary extending northeast of the mesocyclone is produced through evaporative cooling of inflow air and develops last. Con- ceptual models for the simulation were created to demonstrate the evolution and structure of the low-level boundaries. Only the rear-flank gust front may be classified as a ‘‘gust front,’’ defined as having a strong wind shift, delineation between inflow and outflow air, and a strong pressure gradient across the boundary. Trajectory analyses show that parcels traversing the boundary north of the mesocyclone and the rear-flank gust front play a strong role in the development of vertical vorticity existing within the low-level mesocyclone. In addition, baroclinity near the rear-flank downdraft proves to be key in producing horizontal vorticity that is eventually tilted, providing a majority of the positive vertical vorticity within the low-level mesocyclone. 1. Introduction low-level dynamics to assess the development and im- pact of vorticity generated in different parts of the Conceptual models of supercell thunderstorm struc- storm. ture were developed in the late 1970s (Brandes 1978; One of the pioneering modeling studies documenting Lemon and Doswell 1979) and have remained relatively the dynamics of a supercell in detail (with 1-km hori- unchanged. While these conceptual models have gen- zontal grid spacing) was performed by Klemp et al. erally been accepted, verification of boundaries and air (1981). The simulation contained features and structure masses through in situ measurements has been limited that compared well with observations. The ability to because of the difficulty and potential hazards of re- replicate an observed supercell through model simula- cording direct measurements within the storm itself tion solely via a proximity sounding led Klemp et al. (Shabbott and Markowski 2006). Specifically, measure- (1981) to suggest that the larger-scale environment plays ments of low-level thermodynamics have been lacking, an important role in the structure and dynamics of these particularly within the downshear region of the storm. storms. Using similar modeling methods, Klemp and Therefore, the necessity exists for more research of Rotunno (1983) discovered a mechanism through which low-level vertical vorticity is strengthened and sub- sequently repositioned around the simulated low-level Corresponding author address: Jeffrey R. Beck, Centre National de Recherches Me´te´orologiques, Me´te´o-France, DT/AD/RH, 42 mesocyclone. Analysis revealed that low-level air north- Avenue G. Coriolis, 31057 Toulouse CEDEX 1, France. east of the mesocyclone flowed parallel to the ‘‘cold E-mail: [email protected] frontal boundary’’ as it moved toward the low-level DOI: 10.1175/MWR-D-11-00115.1 Ó 2013 American Meteorological Society Unauthenticated | Downloaded 10/06/21 09:59 PM UTC 650 MONTHLY WEATHER REVIEW VOLUME 141 mesocyclone. This boundary was identified by the 218C many different environments in which supercells form perturbation isotherm; therefore, a quantifiable amount most certainly change the low-level evolution and of solenoidally produced horizontal vorticity was pres- boundaries within these storms. Moreover, recent obser- ent in this region of the simulation. A parcel traversing vational studies using Doppler-on-Wheels (DOW) and this boundary acquires significant (mesocyclonic) values Shared Mobile Atmospheric Research and Teaching Ra- of horizontal vorticity in a short period of time (e.g., dar (SMART-R) data (e.g., French et al. 2004; Beck et al. ;300 s). Klemp and Rotunno (1983) found that this 2006; Wurman et al. 2007a,b) have shown variability in horizontal vorticity, with a magnitude comparable to low-level boundary strength within the forward flank of that within the environmental inflow, is subsequently observed storms [many showing the absence of a forward- tilted within the gradient of vertical velocity near the flank gust front (FFGF) in the convergence field]. While mesocyclone, thus enhancing low-level vertical vortic- these studies lacked thermodynamic data, project Verifi- ity. Rotunno and Klemp (1985) found a buoyancy gra- cation of the Origins of Rotation in Tornadoes Experiment dient associated with this cold-air boundary, concluding (VORTEX) collected mobile mesonet measurements that it is important to the solenoidal generation of hor- within a number of supercells. Using the data collected izontal vorticity. during this project, Markowski et al. (2002) documented Wicker and Wilhelmson (1995) found two separate the virtual potential temperature perturbations and origins for parcels with trajectories terminating in the equivalent potential temperature values around hook mesocyclone: one northeast of the mesocyclone, with echoes and the near-mesocyclonic region of supercells. the other aloft, northwest of the mesocyclone, near the Both tornadic and nontornadic storms were sampled, with forward-flank gust front (defined by the authors as the evidence of a gradual east-to-west increase in the virtual 21-K potential temperature isotherm) extending north potential temperature deficit north of each mesocyclone. from the center of rotation. Parcels originating from the The conceptual model presented at the conclusion of the northeast were found to contribute most significantly to study showed a north–south boundary extending out of the vertical vorticity budget of the low-level mesocy- the low-level vertical vorticity maximum, separate from clone. These parcels then traverse a portion of the cold- the rear-flank gust front (RFGF), very similar to Brandes air boundary immediately north of the mesocyclone, (1978). These results mirror those found in Markowski acquiring baroclinically produced horizontal vorticity. et al. (2011), where again a north–south-oriented bound- An earlier paper by Davies-Jones and Brooks (1993) ary was found to exist separate from the RFGF in found that the method in which the baroclinity associ- a number of nontornadic supercell thunderstorms. Finally, ated along the cold-air boundary is tilted ultimately Shabbott and Markowski (2006) studied similar mobile proved fundamental in the production of positive ver- mesonet-collected thermodynamic properties from the tical vorticity near the ground. Specifically, in the pres- forward flank of supercells. A gradual east-to-west in- ence of a rear-flank downdraft, solenoidal generation of crease in density potential temperature deficit was found horizontal vorticity would allow the vorticity vector to exist in many of the storms, but no sharp thermody- within the downdraft to depart from trajectory paths, namic or kinematic boundary was found. Therefore, given resulting in a positive component of vertical vorticity as the discrepancies in forward-flank characteristics and im- the parcel reaches the surface within the downdraft. In plied low-level dynamics between many of these studies, it this sense, the authors’ findings, concerning the impor- is important to focus additional research to determine how tance of baroclinity along the boundary north of the this region of the storm impacts the development of the mesocyclone, mirror those found by Rotunno and Klemp low-level mesocyclone. (1985) and Wicker and Wilhelmson (1995). These results A common thread throughout these research papers is are corroborated by Adlerman et al. (1999), who found a lack of a mutual definition for a baroclinic boundary parcels entering the mesocyclone originate from regions within a supercell. Terms such as cold-frontal or cold-air northwest, north, and northeast of the mesocyclone and boundary, in addition to gust front, are used, sometimes experience positive vertical vorticity tendency upon de- defined using values of perturbation potential temper- scent in the rear-flank downdraft (RFD). ature, or in other cases, the convergence of the wind Established observational conceptual models, along field. However, general consensus is now to use the term with past numerical supercell simulations, have not al- ‘‘gust front’’ as the primary description of a baroclinic ways agreed on low-level baroclinity/boundary strength boundary within a supercell thunderstorm. Per the Glos- and position, specifically within the forward flank. In ad- sary of Meteorology (Glickman 2000), a gust front is de- dition, a spectrum of supercell
Load more

Recommended publications
  • Uplift of Africa As a Potential Cause for Neogene Intensification of the Benguela Upwelling System
    LETTERS PUBLISHED ONLINE: 21 SEPTEMBER 2014 | DOI: 10.1038/NGEO2249 Uplift of Africa as a potential cause for Neogene intensification of the Benguela upwelling system Gerlinde Jung*, Matthias Prange and Michael Schulz The Benguela Current, located o the west coast of southern negligible Neogene uplift of the South African Plateau18. Recently, Africa, is tied to a highly productive upwelling system1. Over for East Africa, evidence emerged for a rather simultaneous the past 12 million years, the current has cooled, and upwelling beginning of uplift of the eastern and western branches around has intensified2–4. These changes have been variously linked 25 million years ago19 (Ma), in contrast to a later uplift of the to atmospheric and oceanic changes associated with the western part around 5 Ma as previously suggested20. Palaeoelevation glaciation of Antarctica and global cooling5, the closure of change estimates, for example for the Bié Plateau, during the the Central American Seaway1,6 or the further restriction of past 10 Myr range from ∼150 m (ref. 16) to 1,000 m (ref.7 ). the Indonesian Seaway3. The upwelling intensification also These discrepancies depend strongly on the methods used for occurred during a period of substantial uplift of the African the estimation of uplift, some giving more reliable estimates of continent7,8. Here we use a coupled ocean–atmosphere general the timing of uplift than of uplift rates16, whereas others are circulation model to test the eect of African uplift on Benguela better suited for estimating palaeoelevations but less accurate upwelling. In our simulations, uplift in the East African Rift in the timing7.
    [Show full text]
  • Navier-Stokes Equation
    ,90HWHRURORJLFDO'\QDPLFV ,9 ,QWURGXFWLRQ ,9)RUFHV DQG HTXDWLRQ RI PRWLRQV ,9$WPRVSKHULFFLUFXODWLRQ IV/1 ,90HWHRURORJLFDO'\QDPLFV ,9 ,QWURGXFWLRQ ,9)RUFHV DQG HTXDWLRQ RI PRWLRQV ,9$WPRVSKHULFFLUFXODWLRQ IV/2 Dynamics: Introduction ,9,QWURGXFWLRQ y GHILQLWLRQ RI G\QDPLFDOPHWHRURORJ\ ÎUHVHDUFK RQ WKH QDWXUHDQGFDXVHRI DWPRVSKHULFPRWLRQV y WZRILHOGV ÎNLQHPDWLFV Ö VWXG\ RQQDWXUHDQG SKHQRPHQD RIDLU PRWLRQ ÎG\QDPLFV Ö VWXG\ RI FDXVHV RIDLU PRWLRQV :HZLOOPDLQO\FRQFHQWUDWH RQ WKH VHFRQG SDUW G\QDPLFV IV/3 Pressure gradient force ,9)RUFHV DQG HTXDWLRQ RI PRWLRQ K KKdv y 1HZWRQµVODZ FFm==⋅∑ i i dt y )ROORZLQJDWPRVSKHULFIRUFHVDUHLPSRUWDQW ÎSUHVVXUHJUDGLHQWIRUFH 3*) ÎJUDYLW\ IRUFH ÎIULFWLRQ Î&RULROLV IRUFH IV/4 Pressure gradient force ,93UHVVXUHJUDGLHQWIRUFH y 3UHVVXUH IRUFHDUHD y )RUFHIURPOHIW =⋅ ⋅ Fpdydzleft ∂p F=− p + dx dy ⋅ dz right ∂x ∂∂pp y VXP RI IRUFHV FFF= + =−⋅⋅⋅=−⋅ dxdydzdV pleftrightx ∂∂xx ∂∂ y )RUFHSHUXQLWPDVV −⋅pdV =−⋅1 p ∂∂ρ xdmm x ρ = m m V K 11K y *HQHUDO f=− ∇ p =− ⋅ grad p p ρ ρ mm 1RWHXQLWLV 1NJ IV/5 Pressure gradient force ,93UHVVXUHJUDGLHQWIRUFH FRQWLQXHG K 11K f=− ∇ p =− ⋅ grad p p ρ ρ mm K K ∇p y SUHVVXUHJUDGLHQWIRUFHDFWVÄGRZQKLOO³RI WKHSUHVVXUHJUDGLHQW y ZLQG IRUPHGIURPSUHVVXUHJUDGLHQWIRUFHLVFDOOHG(XOHULDQ ZLQG y WKLV W\SH RI ZLQGVDUHIRXQG ÎDW WKHHTXDWRU QR &RULROLVIRUFH ÎVPDOOVFDOH WKHUPDO FLUFXODWLRQ NP IV/6 Thermal circulation ,93UHVVXUHJUDGLHQWIRUFH FRQWLQXHG y7KHUPDOFLUFXODWLRQLVFDXVHGE\DKRUL]RQWDOWHPSHUDWXUHJUDGLHQW Î([DPSOHV RYHQ ZDUP DQG ZLQGRZ FROG RSHQILHOG ZDUP DQG IRUUHVW FROG FROGODNH DQGZDUPVKRUH XUEDQUHJLRQ
    [Show full text]
  • Potential Vorticity
    POTENTIAL VORTICITY Roger K. Smith March 3, 2003 Contents 1 Potential Vorticity Thinking - How might it help the fore- caster? 2 1.1Introduction............................ 2 1.2WhatisPV-thinking?...................... 4 1.3Examplesof‘PV-thinking’.................... 7 1.3.1 A thought-experiment for understanding tropical cy- clonemotion........................ 7 1.3.2 Kelvin-Helmholtz shear instability . ......... 9 1.3.3 Rossby wave propagation in a β-planechannel..... 12 1.4ThestructureofEPVintheatmosphere............ 13 1.4.1 Isentropicpotentialvorticitymaps........... 14 1.4.2 The vertical structure of upper-air PV anomalies . 18 2 A Potential Vorticity view of cyclogenesis 21 2.1PreliminaryIdeas......................... 21 2.2SurfacelayersofPV....................... 21 2.3Potentialvorticitygradientwaves................ 23 2.4 Baroclinic Instability . .................... 28 2.5 Applications to understanding cyclogenesis . ......... 30 3 Invertibility, iso-PV charts, diabatic and frictional effects. 33 3.1 Invertibility of EPV ........................ 33 3.2Iso-PVcharts........................... 33 3.3Diabaticandfrictionaleffects.................. 34 3.4Theeffectsofdiabaticheatingoncyclogenesis......... 36 3.5Thedemiseofcutofflowsandblockinganticyclones...... 36 3.6AdvantageofPVanalysisofcutofflows............. 37 3.7ThePVstructureoftropicalcyclones.............. 37 1 Chapter 1 Potential Vorticity Thinking - How might it help the forecaster? 1.1 Introduction A review paper on the applications of Potential Vorticity (PV-) concepts by Brian
    [Show full text]
  • North Sea Barotropic Tides Abstract Strategy of Mixed Meshes
    Modelling of coastal long-wave dynamics on unstructured mixed meshes under strong nonlinearity and pronounced baroclinity Alexey Androsov, Sergey Danilov, Vera Fofonova, Natalja Rakowsky, Karen Helen Wiltshire and Sven Harig Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research, Postfach 12-01-61, 27515 Bremerhaven, Germany, ([email protected] +49(0471) 4831-2106)‏ Abstract Results: North Sea barotropic tides Numerical modelling of coastal zone dynamics provides basis for solving a wide range of hydrogeological, engineering and ecological problems. A novel three-dimensional unstructured-mesh model is applied to simulate the dynamics of the density field and turbulence characteristics. The model is based on a finite-volume discretization and works on mixed unstructured meshes composed of triangles and quads. Although triangular meshes are Fig. 1 Fragments of the quads (left) and mixed (right) mesh used in numerical simulations. most flexible geometrically, quads are more efficient numerically and do not support spurious Fig. 2 Tidal map of the M2 wave: the amplitude in cm and phase (solid line) in inertial modes of triangular cell-vertex discretization. Mixed meshes composed of triangles and Here we present results of simulations of M2 tide in the degrees. The triangles indicate the station locations. A dashed rectangle shows North Sea. A large amount of observations is available the domain where the mesh is refined; the transition zone is over its periphery. quads combine benefits of both. In particular, triangular transitional zones can be used to join for this region helping to validate the model. Computations have been performed on three meshes quadrilateral meshes of differing resolution.
    [Show full text]
  • Chapter 2 Approximate Thermodynamics
    Chapter 2 Approximate Thermodynamics 2.1 Atmosphere Various texts (Byers 1965, Wallace and Hobbs 2006) provide elementary treatments of at- mospheric thermodynamics, while Iribarne and Godson (1981) and Emanuel (1994) present more advanced treatments. We provide only an approximate treatment which is accept- able for idealized calculations, but must be replaced by a more accurate representation if quantitative comparisons with the real world are desired. 2.1.1 Dry entropy In an atmosphere without moisture the ideal gas law for dry air is p = R T (2.1) ρ d where p is the pressure, ρ is the air density, T is the absolute temperature, and Rd = R/md, R being the universal gas constant and md the molecular weight of dry air. If moisture is present there are minor modications to this equation, which we ignore here. The dry entropy per unit mass of air is sd = Cp ln(T/TR) − Rd ln(p/pR) (2.2) where Cp is the mass (not molar) specic heat of dry air at constant pressure, TR is a constant reference temperature (say 300 K), and pR is a constant reference pressure (say 1000 hPa). Recall that the specic heats at constant pressure and volume (Cv) are related to the gas constant by Cp − Cv = Rd. (2.3) A variable related to the dry entropy is the potential temperature θ, which is dened Rd/Cp θ = TR exp(sd/Cp) = T (pR/p) . (2.4) The potential temperature is the temperature air would have if it were compressed or ex- panded (without condensation of water) in a reversible adiabatic fashion to the reference pressure pR.
    [Show full text]
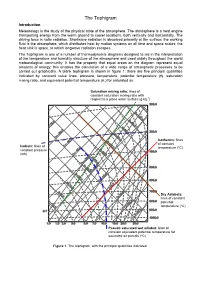
  • The Tephigram Introduction Meteorology Is the Study of the Physical State of the Atmosphere
    The Tephigram Introduction Meteorology is the study of the physical state of the atmosphere. The atmosphere is a heat engine transporting energy from the warm ground to cooler locations, both vertically and horizontally. The driving force is solar radiation. Shortwave radiation is absorbed primarily at the surface; the working fluid is the atmosphere, which distributes heat by motion systems on all time and space scales; the heat sink is space, to which longwave radiation escapes. The Tephigram is one of a number of thermodynamic diagrams designed to aid in the interpretation of the temperature and humidity structure of the atmosphere and used widely throughout the world meteorological community. It has the property that equal areas on the diagram represent equal amounts of energy; this enables the calculation of a wide range of atmospheric processes to be carried out graphically. A blank tephigram is shown in figure 1; there are five principal quantities indicated by constant value lines: pressure, temperature, potential temperature (θ), saturation mixing ratio, and equivalent potential temperature (θe) for saturated air. Saturation mixing ratio: lines of constant saturation mixing ratio with respect to a plane water surface (g kg-1) Isotherms: lines of constant Isobars: lines of temperature (ºC) constant pressure (mb) Dry Adiabats: lines of constant potential temperature (ºC) Pseudo saturated wet adiabat: lines of constant equivalent potential temperature for saturated air parcels (ºC) Figure 1. The tephigram, with the principal quantities indicated. The principal axes of a tephigram are temperature and potential temperature; these are straight and perpendicular to each other, but rotated through about 45º anticlockwise so that lines of constant temperature run from bottom left to top right on the diagram.
    [Show full text]
  • Downloaded 10/01/21 01:41 AM UTC 442 MONTHLY WEATHER REV1 EW Vol
    July 1967 Richard D. Lindzen 441 PLANETARY WAVES ON BETA-PLANES RICHARD D. LINDZEN National Center for Atmospheric Research, Boulder, Colo. ABSTRACT The problem of linearized oscillations of the gaseous envelope of a rotating sphere (with periods in excess of a day) is considered using the @-planeapproximation. Two particular &planes are used-one centered at the equator, the other at a middle latitude. Both forced and free oscillations are considered. With both 8-planes it is possible to approximate known solutions on a sphere. The use of either 8-plane alone, however, results in an inadequate description. In particular it is shown that the equatorial @-planeprovides good approximations to the positive equiv- alent depths of the solar diurnal oscillation, while the midlatitude 8-plane provides good approximations to the negative equivalent depths. The two 8-planes are also used to describe Rossby-Haurwitz waves on rapidly rotating planets, and the vertical propagatability of planetary waves with periods of a day or longer. 1. INTRODUCTION [ll], Dikii [4], Golitsyn and Dikii [7], Lindzen [14], Kato [12], etc.). To a certain extent, even the recent, extensive One of the simplest general types of problems of numerical investigation of Laplace’s Tidal Equation by importance to atmospheric dynamics is that of linearized Longuet-Higgins [15] suffers from these limitations. The wave motions in the gaseous envelope of a rotating sphere. difficulty of the equation has prevented the development The waves are generally taken to be small perturbations of simple formulae of great generality. on a barotropic, motion-free basic state. The pressure is In this paper we shall show that by the use of two generally assumed to be hydrostatic and the fluid is 0-planes-one centered at the equator, the other at some assumed to be inviscid and adiabatic; the horizontal middle latitude-simple relations may be obtained which component of the Earth’s rotation is neglected.
    [Show full text]
  • Dry Adiabatic Temperature Lapse Rate
    ATMO 551a Fall 2010 Dry Adiabatic Temperature Lapse Rate As we discussed earlier in this class, a key feature of thick atmospheres (where thick means atmospheres with pressures greater than 100-200 mb) is temperature decreases with increasing altitude at higher pressures defining the troposphere of these planets. We want to understand why tropospheric temperatures systematically decrease with altitude and what the rate of decrease is. The first order explanation is the dry adiabatic lapse rate. An adiabatic process means no heat is exchanged in the process. For this to be the case, the process must be “fast” so that no heat is exchanged with the environment. So in the first law of thermodynamics, we can anticipate that we will set the dQ term equal to zero. To get at the rate at which temperature decreases with altitude in the troposphere, we need to introduce some atmospheric relation that defines a dependence on altitude. This relation is the hydrostatic relation we have discussed previously. In summary, the adiabatic lapse rate will emerge from combining the hydrostatic relation and the first law of thermodynamics with the heat transfer term, dQ, set to zero. The gravity side The hydrostatic relation is dP = −g ρ dz (1) which relates pressure to altitude. We rearrange this as dP −g dz = = α dP (2) € ρ where α = 1/ρ is known as the specific volume which is the volume per unit mass. This is the equation we will use in a moment in deriving the adiabatic lapse rate. Notice that € F dW dE g dz ≡ dΦ = g dz = g = g (3) m m m where Φ is known as the geopotential, Fg is the force of gravity and dWg is the work done by gravity.
    [Show full text]
  • Introduction to Atmospheric Dynamics Chapter 2
    Introduction to Atmospheric Dynamics Chapter 2 Paul A. Ullrich [email protected] Part 3: Buoyancy and Convection Vertical Structure This cooling with height is related to the dynamics of the atmosphere. The change of temperature with height is called the lapse rate. Defnition: The lapse rate is defned as the rate (for instance in K/km) at which temperature decreases with height. @T Γ ⌘@z Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate For a dry adiabatic, stable, hydrostatic atmosphere the potential temperature θ does not vary in the vertical direction: @✓ =0 @z In a dry adiabatic, hydrostatic atmosphere the temperature T must decrease with height. How quickly does the temperature decrease? R/cp p0 Note: Use ✓ = T p ✓ ◆ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate The adiabac change in temperature with height is T @✓ @T g = + ✓ @z @z cp For dry adiabac, hydrostac atmosphere: @T g = Γd − @z cp ⌘ Defnition: The dry adiabatic lapse rate is defned as the g rate (for instance in K/km) at which the temperature of an Γd air parcel will decrease with height if raised adiabatically. ⌘ cp g 1 9.8Kkm− cp ⇡ Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Lapse Rate This profle should be very close to the adiabatic lapse rate in a dry atmosphere. Paul Ullrich Introduction to Atmospheric Dynamics March 2014 Fundamentals Even in adiabatic motion, with no external source of heating, if a parcel moves up or down its temperature will change. • What if a parcel moves about a surface of constant pressure? • What if a parcel moves about a surface of constant height? If the atmosphere is in adiabatic balance, the temperature still changes with height.
    [Show full text]
  • UC Irvine Faculty Publications
    UC Irvine Faculty Publications Title The modeled response of the mean winter circulation to zonally averaged SST trends Permalink https://escholarship.org/uc/item/89c8g2h3 Journal Journal of Climate, 14(21) Author Magnusdottir, G. Publication Date 2001-11-01 DOI 10.1175/1520-0442(2001)014<4166:TMROTM>2.0.CO;2 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California 4166 JOURNAL OF CLIMATE VOLUME 14 The Modeled Response of the Mean Winter Circulation to Zonally Averaged SST Trends GUDRUN MAGNUSDOTTIR Department of Earth System Science, University of California, Irvine, Irvine, California (Manuscript received 27 July 2000, in ®nal form 23 May 2001) ABSTRACT The response of the atmospheric winter circulation in both hemispheres to changes in the meridional gradient of sea surface temperature (SST) is examined in an atmospheric general circulation model. Climatological SSTs are employed for the control run. The other runs differ in that a zonally symmetric component is added to or subtracted from the climatological SST ®eld. The meridional structure of the variation in SST gradient is based on the observed change in zonally averaged SST over the last century. The SST trend has maxima of about 1 K at high latitudes of both hemispheres. Elsewhere, the increase in SST over the last century is fairly uniform at about 0.5 K. In both hemispheres the response to decreased SST gradients is decreased baroclinity in the lower troposphere and increased baroclinity in the upper troposphere, with the reverse response when the SST gradient is increased.
    [Show full text]
  • Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity
    APRIL 2016 Y U V A L A N D K A S P I 1709 Eddy Activity Sensitivity to Changes in the Vertical Structure of Baroclinicity JANNI YUVAL AND YOHAI KASPI Department of Earth and Planetary Sciences, Weizmann Institute of Science, Rehovot, Israel (Manuscript received 12 May 2015, in final form 25 October 2015) ABSTRACT The relation between the mean meridional temperature gradient and eddy fluxes has been addressed by several eddy flux closure theories. However, these theories give little information on the dependence of eddy fluxes on the vertical structure of the temperature gradient. The response of eddies to changes in the vertical structure of the temperature gradient is especially interesting since global circulation models suggest that as a result of greenhouse warming, the lower-tropospheric temperature gradient will decrease whereas the upper- tropospheric temperature gradient will increase. The effects of the vertical structure of baroclinicity on at- mospheric circulation, particularly on the eddy activity, are investigated. An idealized global circulation model with a modified Newtonian relaxation scheme is used. The scheme allows the authors to obtain a heating profile that produces a predetermined mean temperature profile and to study the response of eddy activity to changes in the vertical structure of baroclinicity. The results indicate that eddy activity is more sensitive to temperature gradient changes in the upper troposphere. It is suggested that the larger eddy sensitivity to the upper-tropospheric temperature gradient is a consequence of large baroclinicity concen- trated in upper levels. This result is consistent with a 1D Eady-like model with nonuniform shear showing more sensitivity to shear changes in regions of larger baroclinicity.
    [Show full text]
  • Nomaly Patterns in the Near-Surface Baroclinicity And
    1 Dominant Anomaly Patterns in the Near-Surface Baroclinicity and 2 Accompanying Anomalies in the Atmosphere and Oceans. Part II: North 3 Pacific Basin ∗ † 4 Mototaka Nakamura and Shozo Yamane 5 Japan Agency for Marine-Earth Science and Technology, Yokohama, Kanagawa, Japan ∗ 6 Corresponding author address: Mototaka Nakamura, Japan Agency for Marine-Earth Science and 7 Technology, 3173-25 Showa-machi, Kanazawa-ku, Yokohama, Kanagawa 236-0001, Japan. 8 E-mail: [email protected] † 9 Current affiliation: Science and Engineering, Doshisha University, Kyotanabe, Kyoto, Japan. Generated using v4.3.2 of the AMS LATEX template 1 ABSTRACT 10 Variability in the monthly-mean flow and storm track in the North Pacific 11 basin is examined with a focus on the near-surface baroclinicity. Dominant 12 patterns of anomalous near-surface baroclinicity found from EOF analyses 13 generally show mixed patterns of shift and changes in the strength of near- 14 surface baroclinicity. Composited anomalies in the monthly-mean wind at 15 various pressure levels based on the signals in the EOFs show accompany- 16 ing anomalies in the mean flow up to 50 hPa in the winter and up to 100 17 hPa in other seasons. Anomalous eddy fields accompanying the anomalous 18 near-surface baroclinicity patterns exhibit, broadly speaking, structures antic- 19 ipated from simple linear theories of baroclinic instability, and suggest a ten- 20 dency for anomalous wave fluxes to accelerate–decelerate the surface west- 21 erly accordingly. However, the relationship between anomalous eddy fields 22 and anomalous near-surface baroclinicity in the midwinter is not consistent 23 with the simple linear baroclinic instability theories.
    [Show full text]