'The Fire Burns Much Better ...' Phd
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Scale Models Brassmasters 4Mm SCALE KITS and FITTINGS
Brassmasters Scale Models PO Box 1137 Sutton Coldfield West Midlands B76 1FU www.brassmasters.co.uk 4mm SCALE KITS AND FITTINGS CATALOGUE AND PRICE LIST 1 May 2018 email : [email protected] TERMS OF TRADE All products listed in this catalogue are available direct by mail order or from our stand at selected exhibitions. Details of the exhibitions we attend are advertised in the model press and on our website. Payment Cash, postal order or cheque with order. Unfortunately, we are unable to accept foreign currency or non - Sterling cheques. Please make your postal orders/cheques payable to " BRASSMASTERS ". We can also accept payments in Sterling by electronic credit into the following UK bank account Name: Brassmasters Scale Models Sort code: 090127 Account number: 74795972 Please contact us first to ensure the items are in stock You may find it useful to download our excel Order Form (make sure you save it to your PC before completing your Please email us when you have made the payment We also accept credit card payments for both UK and overseas customers. Email us with your order and we will send you an iZettle invoice which can be paid using your card. For overseas customers only who do not want to pay via credit card, we can take payment via Paypal - please email us for the post & packing charge. Whilst every effort will be made to supply ex-stock, we will notify you if we cannot deliver your order within twenty- eight days. Please bear in mind that this is a part-time hobby business for us; we try to post out twice weekly, but we only collect our post from the PO Box once each week. -

The Communication Cord
60163 TORNADO 2007 PRINCE OF WALES 3403 ANON New Steam for the Main Line Building Britain’s Most Powerful Steam Locomotive Recreating Gresley’s last design THE COMMUNICATION CORD No. 60 Winter 2021 The rather wonderful sight of one of the Trust’s two new boilers in the X-ray room at DB Meiningen for analysis of the welded seams. DB Meiningen THE RACE IS ON! by Graham Langer There can be no doubt that the Covid-19 push the P2 project over the line it will & Darlington Railway bi-centenary pandemic has had an extremely negative require a final herculean effort in both celebrations during 2025. We need all the impact on the heritage railway movement terms of fundraising and construction to help we can get from our Covenantors and it will probably be some years before ensure that we meet our deadlines, getting and supporters and one of the best ways the financial damage done can be mended No. 2007 Prince of Wales into steam during to achieve this is to bring new people to and The A1 Steam Locomotive Trust has 2022, into traffic by the end of 2023 and the party – after all, it’s not every day you not been entirely immune. If we are to “front and centre” during the Stockton get the chance to be part of history! TCC 1 CONTENTS EDITORIAL by Graham Langer FROM THE CHAIR by Steve Davies PAGE 1 The race is on! “Nothing great will ever be achieved without great men, he Covid-19 essential pipe runs, conduits and the commitment to the P2; second, please and men are great only if they are determined to be so.” situation, and myriad of other small components act as an ambassador on our behalf and PAGE 2 T So said Charles de Gaulle. -

FLYING SCOTSMAN’ LNER 4-6-2 1:32 SCALE • 45 Mm GAUGE
‘FLYING SCOTSMAN’ LNER 4-6-2 1:32 SCALE • 45 mm GAUGE ENGINEERING SAMPLE SHOWN Sir Nigel Gresley was renowned for his Pacific express locomo- SPECIFICATIONS tives, the first of which, the A1 class, entered service in 1922. The A3 was a modification of the A1 and over time all of the sur- Scale 1:32 viving A1s were rebuilt as A3s. No. 4472 “Flying Scotsman” was Gauge 45 mm built in 1923 and went on to become one of the most famous Mini. radius 6ft 6in. (2 m) steam locomotives in the world setting many records along the way. After the war it was renumbered 103 then, after the nation- Dimensions 26.5 x 3.5 x 5.25 in. alisation, carried the number 60103, remaining in service on the Construction Brass & stainless steel East Coast mainline until 1963. During its service career it cov- Electric Version ered over 2,000,000 miles and travelled non-stop from London Power 0~24V DC to Edinburgh in 8 hours. It was sold into private ownership, was Full cab interior design sent to America and Australia and is today under restoration at Features The National Railway Museum in York. Constant lighting Live Steam Version We are currently developing a 1:32 scale live steam version of our very successful electric LNER A3 Class “Flying Scotsman”. Power Live steam, butane fired The model is gas-fired with slide valves and has all the features Boiler Copper the Gauge 1 fraternity have come to expect from an Accucraft Valve gear Walschaerts valve gear locomotive. -

A Brief History of Front-End Research and Latest Developments
A Brief History of Front-End Research and Latest Developments Ir. J.J.G. Koopmans Ph.D. Paper presented during the conference on “Developments in modern Steam Traction” in the National Railway Museum in York, 11th of December 2006. 1 Introduction This paper will cover some of the historic highlights of the development of front-ends during the last 200 years. It is also intended to give a phenomenal description of the functioning of a front-end. Illustration and proof of the examples is provided by some of the results of the tests with the RTM 54 steam locomotive. Notion The discussion is about the use of exhausted steam to create artificial draught in the boiler of steam locomotives. Figure 1 Terence Cuneo's painting of the first steam locomotive The history of the front-end started with Richard Trevithick, who mounted a blast pipe from the cylinders to the chimney, and turned its orifice upwards. The 20th century painting by Terence Cuneo, present in the Welsh National Museum, shows this detail together with the feedwater heater around the blast pipe. The picture shows the joyous moment it represents, but this author has some reservations about the way Trevithick is represented, walking with a spanner in his hand. Locomotive owners and engineers have a common and lasting tendency to be on the locomotive themselves! Some 60- years later the first serious research on the subject was started by Prof. Zeuner1. He used a simplified model of a front-end. During the tests he found that certain dimensional ratios in the front-end gave an asymptotic limit to its performance. -

Full Page Photo
THE LIFE AND TIMES OF A DUKE Martyn J. McGinty AuthorHouse™ UK Ltd. 500 Avebury Boulevard Central Milton Keynes, MK9 2BE www.authorhouse.co.uk Phone: 08001974150 © 2011. Martyn J. McGinty. All rights reserved No part of this book may be reproduced, stored in a retrieval system, or transmitted by any means without the written permission of the author. First published by AuthorHouse 04/25/2011 ISBN: 978-1-4567-7794-4 (sc) ISBN: 978-1-4567-7795-1 (hc) ISBN: 978-1-4567-7796-8 (e) Front Cover Photo: Th e Duke at Didcot (Courtesy P. Treloar) Any people depicted in stock imagery provided by Th inkstock are models, and such images are being used for illustrative purposes only. Certain stock imagery © Th inkstock. Th is book is printed on acid-free paper. Because of the dynamic nature of the Internet, any web addresses or links contained in this book may have changed since publication and may no longer be valid. Th e views expressed in this work are solely those of the author and do not necessarily refl ect the views of the publisher, and the publisher hereby disclaims any responsibility for them. Born out of Tragedy and Riddles, his lineage traceable, unerasable, back through the great houses of Chapelon, Giffard, Stephenson, Belpaire and Watt, the Duke was laid to rust by the sea, a few meagre miles from the mills that shaped the steel that formed the frames that bore the machine that Crewe built. Time passed and the Duke was made well again by kindly strangers. -

The Lner Society
6 0163 TORNADO THE New Steam for the Main Line COMMUNICATION CORD No. 39 Summer 2015 Andrew Southwell Andrew Having taken over from Alycidon in York, Tornado heads the return leg at Great Heck. AN A1 JUBILEE! by Graham Langer After a difficult start to the year it feels would be proved wrong and that by 2014 ‘The Silver Jubilee Talisman’ on Saturday like the sun has come out and is now construction would have started on that 26th September and ‘The Peppercorn shining on the Trust during its Silver organisation’s second, massive, steam Phoenix’ on New Year’s Eve, the former Jubilee Year. Yes, it’s been 25 years since locomotive? The A1 Steam Locomotive a celebration of 25 years of Trust activity, a group of visionaries got together and Trust really has something to celebrate the latter a commemoration of the final decided to do something extraordinary, this year. A1 working by No. 60145 Saint Mungo on to build a brand new main line steam As if all this were not enough, The A1 31st December 1965; why not join us and express locomotive! Who would have Steam Locomotive Trust has been able enjoy some exhilarating East Coast Main thought, back in 1990, that the dream to announce not one, but two more of Line running behind a thoroughbred on would become reality, all the doubters its own railtours in the next six months, her ‘home’ track? TCC 1 by Mark Allatt CONTENTS From the chair by Graham Langer PAgE 1 editorial An A1 Jubilee s I write this years. -

Derby Locomotive Drawings List.Xlsx
Derby Locomotive Drawing Lists Description: The collection consists of approximately 6000 drawings, plus 135 registers and lists. They cover the period from 1874 to 1961. The drawings relate to the construction, modification and rebuilding of locomotives of the Midland Railway, London Midland & Scottish Railway and British Railways, with occasional drawings from other railway companies and contractors. The drawings are mainly on linen with some blueprints, as well as Ozalid and paper copies. Each drawing has a number and/ or a letter code. These letter and number codes also relate to the registers, schedules and lists. The significance of these codes is explained in the ‘System of Arrangement’ section below. System of Arrangement: The drawings are arranged in the archive in five series and are listed as such in the catalogue. 1. Main Series. These are organised by drawing number in numerical sequence. Most drawings have a two number date prefix that usually relates to the year in which the drawing was produced, but may sometimes relate to the year the drawing was entered in the register. 2. D Numerical series. These are also organised by drawing number, but prefixed by the section reference, such as D1, D2, D3, D4 or D5. 3. Diagrams and Sketches. These are also organised by drawing number, but prefixed according to the section reference code, such as DS, DD, S, D or ED. 4. BR Standard Drawings from Derby. These drawings are proper to the main collection of British Rail Standard Drawings, but were found with the main Derby Works sequences. They are numerical with the prefix SL/DE. -

Great Steam Locomotives
Great Steam Locomotives Since George Stephenson’s Locomotion No. 1 carried its first excited passengers along the Stockton to Darlington railway in 1825, Britain has loved steam locomotives. Railways travelled by steam locomotives let people travel further than they had ever done before and businesses could now transport their goods to market much more quickly. Many great steam locomotives were made and some of them are still famous today. Rocket Flying Scotsman In 1829 father and son team George and Robert The Flying Scotsman was designed by Sir Nigel Stephenson entered their steam locomotive, Rocket, Gresley and built in Doncaster in 1923. The into the Rainhill Trials. This was a competition Flying Scotsman was named because it provided to find a locomotive for the new Liverpool to The Flying Scotsman passenger service between Manchester Railway line. Six locomotives started London and Edinburgh. the competition but the Rocket won. The Flying Scotsman was the first steam To many people the Rocket will always be the locomotive to travel non-stop from London to greatest steam locomotive. It was the fastest of its Edinburgh in 1928 and in 1934 it was the first day reaching a record speed of 29 miles per hour steam locomotive to reach a top speed of 100 in the Rainhill trials. miles per hour. Mallard Evening Star The Mallard was another of Sir Nigel Gresley’s The Evening Star was famous before it was even designs. It was very fast, sleek and could pull long built in 1960 because it was to be the last steam passenger trains at more than 100 miles per hour. -

Lms Locomotives
LMS LOCOMOTIVES PART 1 Standard Classes LENS OF SUTTON ASSOCIATION List 22 (Issue 2 November 2009) LMS 9673 circa 1930s (24445) L.O.S.A. List 22 LMS Locos Part 1 Page 1 THE LENS OF SUTTON ASSOCIATION LMS Locomotives Part 1 The Standard Classes This catalogue lists the Standard LMS steam locomotive classes The order of data for each entry is as follows: Negative number, locomotive number, locomotive name if applicable, date if known, aspect of locomotive in the photograph (right or left; ¾, broadside or head on; front or rear), location if known, any other relevant comment, eg livery FOWLER Class 3 2-6-2T 40054 at Clapham Junction c1954 (23052) 23000 LMS 15520 early 30's L3/4f shed view 23001 LMS 15527 early 30's R3/4f inside roundhouse 23002 LMS 15530 early 30's L3/4f Kentish Town Shed 24447 LMS 15532 early 30's L3/4f St.Pancras Station, heading local passenger 23003 LMS 15550 early 30's L3/4f shed view 23004 LMS 15552 early 30's L3/4f shed view 23005 LMS 2 late 30's L3/4f shed view 23006 LMS 3 late 30's R3/4f shed view; Copy 23007 LMS 3 c1935 R3/4f shed view 23008 LMS 10 c1947 R3/4f Watford Junction 23009 LMS 16 c1947 R3/4f Walsall Shed 23010 LMS 16 late 30's R3/4f shed view 23011 LMS 17 18.8.35 R3/4f Walsall Shed 23012 LMS 17 c1947 R3/4f Walsall Shed 23013 LMS 22 late 40's L3/4f station view, running bunker first on local passenger 23014 LMS 22 late 40's R3/4f Cricklewood Shed 23015 LMS 22 late 30's L3/4f Kentish Town Shed 23016 LMS 23 late 30's L3/4f shed view 23017 LMS 24 late 30's L3/4f Kentish Town Shed L.O.S.A. -

Glorious Trains Part Two
Hugo Marsh Neil Shuttleworth Thomas Forrester Director Director Director Glorious Trains Part Two Tuesday 29th June 2021 at 10.00 Special Auction Services Contact the below specialists for further information: Plenty Close Off Hambridge Road NEWBURY RG14 5RL Telephone: 01635 580595 Email: [email protected] www.specialauctionservices.com Dominic Foster Graham Bilbe Bob Leggett Toys Trains Toys,Trains & Figures Due to the nature of the items in this auction, buyers must satisfy themselves concerning their authenticity prior to bidding and returns will not be accepted, subject to our Terms and Conditions. Additional images are available on request. Buyers Premium with SAS & SAS LIVE: 20% plus Value Added Tax making a total of 24% of the Hammer Price the-saleroom.com Premium: 25% plus Value Added Tax making a total of 30% of the Hammer Price 1. A Hornby 0 Gauge No 3E 6-volt 6. A converted Hornby 0 Gauge No 10. An assortment of Hornby 0 AC ‘Flying Scotsman’ Locomotive only, an O Locomotive and Tender, both in Great Gauge Clockwork Mechanisms, including early example with external brush-caps to Western lined green, the early loco without an early No 2 motor fitted for ‘Control’ the right side, black smokebox and plain cylinders as no 2251, originally clockwork operation (from 4-4-0 or 4-4-4T), lacks gold numbers to cab-sides, G-VG, light and now fitted with an original Hornby control rods otherwise G-VG, with three playwear, very slight damage to front right 20v electric mechanism with replacement No 1 motor units (nickelled sides) -

Trains Galore
Hugo Marsh Neil Thomas Forrester (Director) Shuttleworth (Director) (Director) Trains Galore 11th & 12th December 2018 at 10:00 Viewing: 10th December 2018 10:00-16:00 11th December 2018 10:00- 16:00 16:00-18:00 Mulled Wine, Mince Pies & Nibbles 12th December 2018 Morning of auction from 9:00 Otherwise by appointment Saleroom One 81 Greenham Business Park NEWBURY RG19 6HW Telephone: 01635 580595 Fax: 0871 714 6905 Email: [email protected] www.specialauctionservices.com Bob Leggett Graham Bilbe Dominic Foster Toys, Trains & Trains Toys & Trains Figures Bid Here Without Being Here All you need is your computer and an internet connection and you can make real-time bids in real-world auctions at the-saleroom.com. You don’t have to be a computer whizz. All you have to do is visit www.the-saleroom.com and register to bid - its just like being in the auction room. A live audio feed means you hear the auctioneer at exactly the same time as other bidder. You see the lots on your computer screen as they appear in the auction room, and the auctioneer is aware of your bids the moment you make them. Just register and click to bid! ORDER OF AUCTION DAY ONE : 11th December 2018 N Gauge 1-57 TT Gauge 58-124 HOn3, HOm & On3O Gauge 125-147 Hornby OO Gauge 148-277 Lima OO & HO Gauge 278-300 Bachmann OO Gauge 301-381 Hornby-Dublo 382-452 Hornby-Dublo Catalogues 453-459 Wrenn OO Gauge 460-469 Other OO Gauge 470-522 Kitbuilt OO Gauge 523-584 HO Gauge 585-717 American HO Gauge 718-736 DAY TWO: 12th December 2018 Railwayana 737-806 Railway Pictures, Prints & Books 807-827 Penny Toys, Floor Trains & S Gauge 828-835 Hornby O Gauge 836-909 Bassett-Lowke 910-937 Modern O Gauge 938-989 Finescale O Gauge 990-1099 Other O Gauge 1100-1236 Gauge I 1237-1315 LGB & Other Garden Railway 1316-1332 Wide Gauges & Live Steam 1333-1414 Buyers Premium: 17.5% plus Value Added Tax making a total of 21% of the Hammer Price Internet Buyers Premium: 22.5% plus Value Added Tax making a total of 27% of the Hammer Price 2 www.specialauctionservices.com N GAUGE 14. -
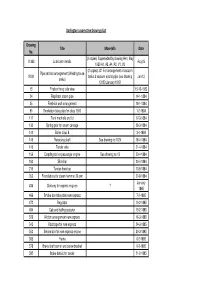
Darlington Locomotive Drawings List.Xlsx
Darlington Locomotive Drawings List Drawing Title More Info Date No. (2 copies) Superseded by drawing H41, May 11363 Lubricator details Aug-25 1939 A1, A3, A4, P2, V1, V2 (2 copies) J21 For arrangement of vacuum Pipe and rod arrangement (Westinghouse 8108 brake & vacuum ejector pipe (see drawing Jan-12 brake) 13123 January 1912) 15 Firebox fixing side view 15-12-1883 24 Regulator steam pipe 14-1-1884 35 Firebrick arch arrangement 18-1-1884 90 Smokebox tube plate for class 1500 1-2-1884 117 Tank manhole and lid 17-3-1884 130 Spring gear for steam carriage 28-3-1884 140 Boiler class 8 3-4-1884 146 Reversing shaft See drawing no 1024 18-4-1884 149 Tender axle 21-4-1884 156 Coupling rod ex passenger engine See drawing no 13 23-4-1884 163 Slide bar 24-4-1884 219 Tender draw bar 13-6-1884 352 Foundations for steam hammer 20 cwt 20-8-1884 January 434 Chimney for express engines ? 1885 466 Smoke box tube plate new express 7-2-1885 472 Regulator 10-2-1885 494 Cab and trailing splasher 19-2-1885 526 Motion arrangement new express 16-3-1885 543 Blast pipe for new express 24-3-1885 553 Smoke box for new express engine 30-3-1885 566 Frame 6-2-1885 578 Brake shaft carrier and screw bracket 9-3-1885 582 Brake details for tender 21-2-1885 Darlington Locomotive Drawings List Drawing Title More Info Date No. 594 Screw coupling and side chain 15-3-1885 Arrangement of ashpan and firebars new 600 17-4-1885 express Whistle gear and cab handrail for new 617 25-4-1885 express Smoke box arrangement for new express 628 2-5-1885 engine 635 Deflecting plate for