The Residence Time of the Water in Lago Maggiore (N. Italy): First Results from an Eulerian-Lagrangian Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Franklin University Switzerland Student Handbook 2020-2021
STUDENT HANDBOOK 2021-2022 ACADEMIC YEAR MISSION The Office of Student Life facilitates student learning and development through intercultural opportunities, immigration support, health and wellness services, and other co-curricular experiences. ABOUT US We know that student engagement outside the classroom is critical to success in the classroom and in life. Our programs and services are designed to help students achieve their academic goals; engage in experiential learning; develop intercultural maturity; cultivate relationships within Franklin and the surrounding communities; exhibit civic responsibility, and graduate with a stronger sense of cross-cultural perspectives that allows them to build careers that take them beyond national boundaries. EQUAL OPPORTUNITIES Franklin University Switzerland is committed to the principle of equal opportunity and to providing an academic and work environment free from discrimination. The University prohibits discrimination on the basis of race, color, national or ethnic origin, religion, sex, sexual orientation, gender identity or gender expression, age, disability, and other legally protected statuses. LEARNING OUTCOMES Students will be able to: • Demonstrate an understanding of, and develop relationships within, the Franklin and surrounding communities while utilizing Franklin and local community resources. • Demonstrate civic responsibility, ownership, and accountability on and off campus. • Display intercultural maturity in all aspects of your life. • Demonstrate the ability to contribute to -
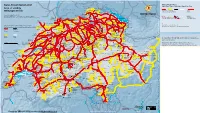
Swiss Travel System Map 2021
ai160326587010_STS-GB-Pass-S-21.pdf 1 21.10.20 09:37 Kruth Strasbourg | Paris Karlsruhe | Frankfurt | Dortmund | Hamburg | Berlin Stuttgart Ulm | München München Swiss Travel System 2021 Stockach Swiss Travel Pass Blumberg-Zollhaus Engen Swiss Travel Pass Youth | Swiss Travel Pass Flex Bargen Opfertshofen Überlingen Area of validity Seebrugg Beggingen Singen Ravensburg DEUTSCHLAND Radolfzell Schleitheim Hemmental Lines for unlimited travel (tunnel) Mulhouse Thayngen Mainau Geltungsbereich Meersburg Schaffhausen Ramsen Linien für unbegrenzte Fahrten (Tunnel) Zell (Wiesental) Wangen (Allgäu) Erzingen Oster- Neuhausen Stein a.R. Konstanz fingen Version/Stand/Etat/Stato:12.2020 (Baden) Rheinau Kreuzlingen Friedrichshafen Waldshut Due to lack of space not all lines are indicated. Subject to change. Marthalen Basel Weil a.R. Aus Platzgründen sind nicht alle Linien angegeben. Änderungen vorbehalten. Bad Zurzach Weinfelden Lines with reductions (50%, 1 25%) No reductions EuroAirport Riehen Koblenz Eglisau Frauenfeld Romanshorn Lindau Basel St.Johann Basel Möhlin Laufenburg Immenstadt Linien mit Vergünstigungen (50%, 1 25%) Keine Ermässigung Bad Bf Nieder- Stein-Säckingen Bülach Sulgen Arbon Basel Rheinfelden weningen Braunau Sonthofen Delle Pratteln Turgi Rorschach Bregenz Boncourt Ettingen Frick Brugg Zürich Bischofszell Rheineck Bonfol Liestal Baden Flughafen Winterthur Wil Rodersdorf Dornach Oberglatt Heiden St.Margrethen Aesch Gelterkinden Kloten Turbenthal St.Gallen Walzenhausen Roggenburg Wettingen Also valid for local public transport -
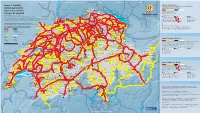
Swiss Pass Validity
Strasbourg | Paris | Luxembourg | Bruxelles Karlsruhe | Frankfurt | Dortmund | Hamburg | Berlin Stuttgart Ulm | München München Area of validity Stockach Swiss Travel Pass Swiss Travel Pass Youth | Swiss Travel Pass Flex | Swiss Travel Pass Flex Youth Geltungsbereich Ravensburg Beggingen Singen DEUTSCHLAND Thayngen Radolfzell Insel Lines for unlimited travel Rayon de validité Mulhouse Schleitheim Mainau Schaffhausen Meersburg Linien für unbegrenzte Fahrten Zell (Wiesental) Lignes avec utilisation illimitée Campo di validità Neuhausen Stein a.R. Konstanz Erzingen Linee per corse illimitate Version/Stand/Etat/Stato: 10. 2014 (Baden) Rheinau Kreuzlingen Friedrichshafen Waldshut Due to lack of space not all lines are indicated. Subject to change. Marthalen Basel Weil a. R. Aus Platzgründen sind nicht alle Linien angegeben. Änderungen vorbehalten. Bad Zurzach Weinfelden Lines with reductions (50%, 1 25%) No reductions EuroAirport Riehen Koblenz Eglisau Frauenfeld Romanshorn Lindau Pour des raisons de place, toutes les lignes ne sont pas indiquées. Sous réserve de modifications. Basel St. Johann Basel Möhlin Laufenburg Immenstadt Linien mit Vergünstigungen (50%, 1 25%) Keine Ermässigung Bad Bf Nieder- Lignes avec réductions (50%, 1 25%) Aucune réduction Per motivi di spazio, non tutte le linee sono presenti. Con riserva di modifiche. R’felden Stein-Säckingen Bülach Sulgen Arbon Basel weningen Sonthofen Linee che prevedono sconti (50%, 1 25%) Nessuno sconto Delle Pratteln Turgi Rorschach Bregenz Boncourt Ettingen Frick Brugg Bischofszell Rheineck -

Dynamic Modelling of the Fate of DDT in Lake Maggiore: Preliminary Results
Dynamic modelling of the fate of DDT in Lake Maggiore: Preliminary results S. Dueri, J. M. Zaldívar and A. Olivella Institute for Environment and Sustainability 2005 EUR 21663 EN 1 The mission of the Institute for Environment and Sustainability is to provide scientific and technical support to EU policies for the protection of the environment contributing to sustainable development in Europe. European Commission Directorate-General Joint Research Centre Institute for Environment and Sustainability Contact information Address:Via E. Fermi 1, TP 272 E-mail: [email protected] Tel.:+39-0332789202 Fax: +39-0332785807 http://ies.jrc.cec.eu.int http://www.jrc.cec.eu.int Legal Notice Neither the European Commission nor any person acting on behalf of the Commission is responsible for the use which might be made of this publication. A great deal of additional information on the European Union is available on the Internet. It can be accessed through the Europa server http://europa.eu.int EUR 21663 EN Luxembourg: Office for Official Publications of the European Communities © European Communities, 2005 Reproduction is authorised provided the source is acknowledged Printed in Italy 2 CONTENTS 1. INTRODUCTION 4 2. FATE AND TRANSPORT OF DDT: MASS BALANCE MODEL 5 2.1 Sorptium equilibria 7 2.2 Air-Water Exchange 8 2.3 Dry and wet deposition 12 2.4 Sediment deposition: Settling 13 2.5 Sediments-Water Exchange 13 2.6 Resuspension and burial 15 2.7 Pore water diffusion 16 2.8 Sediment biodiffusion 16 2.9 Chemical loss rate 17 3. LAKE MAGGIORE PARAMETERS AND BOUNDARY DATA 17 3.1. -

List of Rivers of Italy
Sl. No Name Draining Into Comments Half in Italy, half in Switzerland - After entering Switzerland, the Spöl drains into 1 Acqua Granda Black Sea the Inn, which meets the Danube in Germany. 2 Acquacheta Adriatic Sea 3 Acquafraggia Lake Como 4 Adda Tributaries of the Po (Left-hand tributaries) 5 Adda Lake Como 6 Adige Adriatic Sea 7 Agogna Tributaries of the Po (Left-hand tributaries) 8 Agri Ionian Sea 9 Ahr Tributaries of the Adige 10 Albano Lake Como 11 Alcantara Sicily 12 Alento Adriatic Sea 13 Alento Tyrrhenian Sea 14 Allaro Ionian Sea 15 Allia Tributaries of the Tiber 16 Alvo Ionian Sea 17 Amendolea Ionian Sea 18 Amusa Ionian Sea 19 Anapo Sicily 20 Aniene Tributaries of the Tiber 21 Antholzer Bach Tributaries of the Adige 22 Anza Lake Maggiore 23 Arda Tributaries of the Po (Right-hand tributaries) 24 Argentina The Ligurian Sea 25 Arno Tyrrhenian Sea 26 Arrone Tyrrhenian Sea 27 Arroscia The Ligurian Sea 28 Aso Adriatic Sea 29 Aterno-Pescara Adriatic Sea 30 Ausa Adriatic Sea 31 Ausa Adriatic Sea 32 Avisio Tributaries of the Adige 33 Bacchiglione Adriatic Sea 34 Baganza Tributaries of the Po (Right-hand tributaries) 35 Barbaira The Ligurian Sea 36 Basentello Ionian Sea 37 Basento Ionian Sea 38 Belbo Tributaries of the Po (Right-hand tributaries) 39 Belice Sicily 40 Bevera (Bévéra) The Ligurian Sea 41 Bidente-Ronco Adriatic Sea 42 Biferno Adriatic Sea 43 Bilioso Ionian Sea 44 Bisagno The Ligurian Sea 45 Biscubio Adriatic Sea 46 Bisenzio Tyrrhenian Sea 47 Boesio Lake Maggiore 48 Bogna Lake Maggiore 49 Bonamico Ionian Sea 50 Borbera Tributaries -

Pescare Nel Bacino 5 (Verbano
ANNO 2020 2 INDIRIZZI UTILI E RIFERIMENTI TERRITORIALI AGRICOLTURA, CACCIA E PESCA INSUBRIA -Varese Orario di apertura al pubblico: Viale Belforte, 22 ▪ da lunedì a venerdì: 09.00 - 12.30 21100 VARESE (VA) ▪ Mercoledì: 14.30 - 16.30 Attività: gestione faunistica Sportello Utenza: 0332.338367 [email protected] AGRICOLTURA, CACCIA E PESCA INSUBRIA -Como Orario di apertura al pubblico: Via L. Einaudi, 1 ▪ da lunedì a venerdì: 09.00 - 12.30 22100 COMO (CO) Attività: gestione faunistica ▪ Mercoledì: 14.30 - 16.30 Sportello Utenza: 031.320570 [email protected] AGRICOLTURA, CACCIA E PESCA Brianza -Lecco Corso Promessi Sposi, 132, Orario di apertura al pubblico: 23900 LECCO (LC) ▪ da lunedì a venerdì: 09.00 - 12.30 Attività: gestione faunistica ▪ Mercoledì: 14.30 - 16.30 Sportello Utenza: 0341.358946 [email protected] PESCARE NEL BACINO 5 – VERBANO LARIO CERESIO 4 PESCARE NEL BACINO 5 – VERBANO LARIO CERESIO PREMESSA Questa pubblicazione ha carattere divulgativo e non legale; essa riassume i regolamenti di pesca in vigore nel bacino n° 5 -Verbano, Lario, Ceresio- al 1 gennaio 2020 Il bacino 5 comprende la porzione lombarda dei laghi Verbano, Ceresio, Lario e i laghi Mezzola, Garlate e Olginate, Varese, Comabbio, Monate, Montorfano, Alserio, Segrino, Piano, Pusiano, Annone, con i loro tributari. Sono escluse tutte le acque che ricadono nella Provincia di Sondrio. Appartengono al bacino 5 il fiume Adda immissario nel tratto compreso fra il Lario e il confine con la provincia di Sondrio, il fiume Adda emissario fino al nuovo Ponte ferroviario del Lavello, il fiume Ticino fino al ponte di Sesto Calende, il fiume Olona fino al ponte di Vedano e il fiume Lambro fino al ponte di Nibionno sulla Sp 342. -

Piano Sociale Di Zona Ambito Di Luino
Piano Sociale di Zona Ambito di Luino Assemblea dei Sindaci 2018 - 2020 Agra Bedero Valcuvia Brezzo di Bedero Brissago Valtravaglia Cadegliano Viconago Castelveccana Cremenaga Cugliate Fabiasco Cunardo Curiglia con Monteviasco Dumenza Ferrera di Varese Germignaga Grantola Lavena Ponte Tresa Luino Maccagno con Pino e Veddasca Marchirolo Marzio Mesenzana Montegrino Valtravaglia Porto Valtravaglia Tronzano Lago Maggiore Valganna Indice CAPITOLO 1 GLI ESITI DELLA PROGRAMMAZIONE NEL TRIENNIO 2015-2017 Le attività di programmazione………………………………………………………………………………………. p. 1 La valutazione delle attività ricompositive del sistema di conoscenza ………………………. p. 1 I soggetti …..………………………………………………………………………………………………………………………… p. 1 Gli obiettivi .……………………………………………………………………………………………………………………….. p. 1 I risultati .……………………………………………………….……………………………………………………………………. p. 2 La valutazione delle attività ricompositive dei percorsi a favore dei fruitori del sistema di servizi/interventi/prestazioni ……………………………………………………………………… p. 2 Gli obiettivi .……………………………………………………………………………………………………………………….. p. 2 I risultati .……………………………………………………….……………………………………………………………………. p. 3 La valutazione delle attività ricompositive delle risorse ….………………………………………….. p. 3 Gli obiettivi .……………………………………………………………………………………………………………………….. p. 3 I risultati .……………………………………………………….……………………………………………………………………. p. 4 La valutazione degli interventi/progetti/servizi previsti in fase di programmazione, sia zonali sia sovra zonali………………. ….……………………………….................................... p. 4 I Servizi .………………………………………………………………………………………………………………………………. -

Rechtssache T-304/13 P: Rechtsmittel, Eingelegt Am 31. Mai 2013 Von
24.8.2013 DE Amtsblatt der Europäischen Union C 245/9 Urteil des Gerichts vom 10. Juli 2013 — Kreyenberg/ Alvarez Alvarez (Besozzo), Salvatore Amato (Lavagna, Italien), HABM — Kommission (MEMBER OF €e euro experts) Angiola Amore (Angera, Italien), Giuseppe Amoruso (Besozzo), Michel Amsellem (Sangiano, Italien), Fivos Andritsos (Gavirate, (Rechtssache T-3/12) ( 1 ) Italien), Alessandro Annoni (Laveno, Italien), Massimo Anselmi (Sesto Calende, Italien), Carlo Antoniotti (Orino, Italien), Aldo (Gemeinschaftsmarke — Nichtigkeitsverfahren — Gemein Ardia (Besozzo), Fernando Arroja (Varese, Italien), Karin Asch schaftsbildmarke MEMBER OF €e euro experts — Absolutes berger (Ranco, Italien), Andreas Aschberger (Ranco), Heikki Au Eintragungshindernis — Embleme der Union und ihrer Tätig lamo (Besozzo), Davide Auteri (Varese), Roberto Babich (Gavi keitsbereiche — Euro-Zeichen — Art. 7 Abs. 1 Buchst. i der rate), Valentino Bada (Ispra), Vagn Bak-Mikkelsen (Angera), Si Verordnung (EG) Nr. 207/2009) mone Bano (Mornago, Italien), Joaquin Baraibar (Ispra), Vittorio Barale (Vercelli, Italien), Stefano Baranzini (Angera), Thomas Barbas (Varese), Caterina Barbera (Laveno), Marco Barbero (Ver (2013/C 245/12) bania, Italien), Paulo Barbosa (Ispra), Elena Bardelli (Monvalle, Italien), Renzo Bardelli (Besozzo), Jose Ignacio Barredo Cano Verfahrenssprache: Deutsch (Ispra), Marco Basso (Varano Borghi, Italien), Maurizio Bavetta (Cadrezzate, Italien), Claudio Belis (Ispra), Carlo Bellora (Mai land, Italien), Alan Belward (Cittiglio), Zita Bemova (Taino, -

Agra Angera Azzate Barasso Bardello Bedero Valcuvia Besano Besozzo
va AREA 4 - AMBIENTE E TERRITORIO Settore Energia, Rifiuti, Risorse Idriche Ufficio Tutela Acque Referente pratica: Ing. Roberta Peroni Tel. 0332/252914 Varese, lì 18 giugno 2019 Prot. n. «PEC» Classificazione 9.8.2 Nell’eventuale risposta citare il numero di protocollo e la classificazione sopraindicati. Egr. Sig. Sindaco del Comune di Agra Angera Azzate Barasso Bardello Bedero Valcuvia Besano Besozzo Biandronno Bodio Lomnago Brebbia Bregano Brezzo di Bedero Brinzio Brusimpiano Buguggiate Cadegliano Viconago Cadrezzate con Osmate Casale Litta Casciago Castelveccana Cazzago Brabbia Cittiglio Comabbio Comerio Cuasso al Monte Cugliate Fabiasco Cunardo Dumenza Galliate Lombardo Gavirate - 1 - Provincia di Varese, Piazza Libertà, 1 - 21100 Varese - Tel 0332 252111 C.F. n. 80000710121 - P.I. n. 00397700121 - www.provincia.va.it - [email protected] Germignaga Inarzo Ispra Lavena Ponte Tresa Laveno Mombello Leggiuno Luino Maccagno con Pino e Veddasca Mercallo Monvalle Porto Ceresio Porto Valtravaglia Ranco Sesto Calende Taino Ternate Travedona Monate Tronzano Lago Maggiore Valganna Varano Borghi Varese Vergiate e p.c. Spett.le Ufficio d'Ambito della Provincia di Varese [email protected] Oggetto: Regolamento Regionale n. 6 del 29 marzo 2019. Richiesta di collaborazione per la diffusione delle nuove disposizioni in materia di acque reflue domestiche nella fascia dei laghi. Con la presente si informa che la Regione Lombardia ha emanato il Regolamento 29 marzo 2019, n. 6 (BURL del 2/04/2019 - Suppl. n. 14) "Disciplina e regimi amministrativi degli scarichi di acque reflue domestiche e di acque reflue urbane, disciplina dei controlli degli scarichi e delle modalità di approvazione dei progetti degli impianti di trattamento delle acque reflue urbane", il quale è entrato in vigore il 3 aprile u.s. -

62.429 Ponte Tresa - Fornasette - Luino (I) Stato: 11
ANNO D'ORARIO 2021 62.429 Ponte Tresa - Fornasette - Luino (I) Stato: 11. Marzo 2021 201 203 205 207 209 211 213 215 217 219 221 Ponte Tresa, Stazione 05 53 06 23 06 40 07 10 07 40 08 10 09 10 10 10 11 10 12 10 13 10 Ponte Tresa, Dogana 05 53 06 23 06 40 07 10 07 40 08 10 09 10 10 10 11 10 12 10 13 10 Barico, Bivio per Barico 05 56 06 26 06 43 07 13 07 43 08 13 09 13 10 13 11 13 12 13 13 13 Madonna del Piano, Paese 05 58 06 28 06 45 07 15 07 45 08 15 09 15 10 15 11 15 12 15 13 15 Molinazzo di Monteggio, 06 00 06 30 06 47 07 17 07 47 08 17 09 17 10 17 11 17 12 17 13 17 Posta Ponte Cremenaga, Paese 06 02 06 32 06 49 07 19 07 49 08 19 09 19 10 19 11 19 12 19 13 19 Fornasette, 06 05 06 35 06 52 07 22 07 52 08 22 09 22 10 22 11 22 12 22 13 22 Villaggio vacanze Fornasette, 06 06 06 36 06 53 07 23 07 53 08 23 09 23 10 23 11 23 12 23 13 23 Dogana Svizzera Luino, Centro Sportivo (I) 06 11 06 41 06 58 07 28 07 58 08 28 09 28 10 28 11 28 12 28 13 28 Luino, Piazza Libertà (I) 06 15 06 45 07 02 07 32 08 02 08 32 09 32 10 32 11 32 12 32 13 32 Luino, Stazione FS (I) 06 20 06 50 07 07 07 37 08 07 08 37 09 37 10 37 11 37 12 37 13 37 223 225 227 229 231 233 235 237 239 241 243 Ponte Tresa, Stazione 14 10 15 10 16 10 17 10 17 40 18 10 18 40 19 10 20 10 21 10 22 10 Ponte Tresa, Dogana 14 10 15 10 16 10 17 10 17 40 18 10 18 40 19 10 20 10 21 10 22 10 Barico, Bivio per Barico 14 13 15 13 16 13 17 13 17 43 18 13 18 43 19 13 20 13 21 13 22 13 Madonna del Piano, Paese 14 15 15 15 16 15 17 15 17 45 18 15 18 45 19 15 20 15 21 15 22 15 Molinazzo di Monteggio, 14 -

Twenty-Year Sediment Contamination Trends in Some Tributaries of Lake Maggiore (Northern Italy): Relation with Anthropogenic Factors
Environmental Science and Pollution Research https://doi.org/10.1007/s11356-021-13388-6 RESEARCH ARTICLE Twenty-year sediment contamination trends in some tributaries of Lake Maggiore (Northern Italy): relation with anthropogenic factors Laura Marziali1 & Licia Guzzella1 & Franco Salerno1 & Aldo Marchetto2 & Lucia Valsecchi 1 & Stefano Tasselli1,3 & Claudio Roscioli1 & Alfredo Schiavon1,4 Received: 3 November 2020 /Accepted: 8 March 2021 # The Author(s), under exclusive licence to Springer-Verlag GmbH Germany, part of Springer Nature 2021 Abstract Lake tributaries collect contaminants from the watershed, which may accumulate in lake sediments over time and may be removed through the outlets. DDx, PCB, PAH, PBDE, and trace element (Hg, As, Cd, Ni, Cu, Pb) contamination was analyzed over 2001– 2018 period in sediments of the 5 main tributaries and of the outlet of Lake Maggiore (Northern Italy). Sediment cores were collected in two points of the lake, covering 1995–2017 period. Concentrations were compared to Sediment Quality Guidelines (PECs), potential sources and drivers (land use, population numbers, industrial activities, hydrology) were analyzed, and temporal trends were calculated (Mann-Kendall test). PCB, PBDE, Pb, Cd, and Hg contamination derives mainly from heavy urbanization and industry. Cu and Pb show a temporal decreasing trend in the basin, likely as result of improved wastewater treatments and change in use. A recent PAH increase in the whole lake may derive from a single point source. A legacy DDx and Hg industrial pollution is still present, due to high persistence in sediments. Values of DDx, Hg, Pb, and Cu above the PECs in lake sediments and/or in the outlet show potential risk for aquatic organisms. -

3 Maggio 2020 Lmit
3 MAGGIO 2020 LMIT - KM 55 D+ 4.170 m LMIminiT - KM 20 D+ 1.430 m OGNI CONCORRENTE CON L’ISCRIZIONE DICHIARA DI CONOSCERE E ACCETTARE IL PRESENTE REGOLAMENTO SENZA RISERVE. 1 - INFORMAZIONI GENERALI Il LAGO MAGGIORE INTERNATIONAL TRAIL e il LAGO MAGGIORE INTERNATIONAL mini TRAIL sono organizzati dall' A.S.D. Val Veddasca e MolineraRunning. La manifestazione può fregiarsi del patrocinio della Comunità Montana Valli del Verbano e dei Comuni di Maccagno con Pino e Veddasca / Tronzano Lago Maggiore / Curiglia con Monteviasco / Dumenza (facenti parte della Provincia di Varese). Le gare competitive sono due: *LAGO MAGGIORE INTERNATIONAL TRAIL (LMIT) 55 Km con 4.170 m D+; - Valore ITRA 3, per la CCC (“Courmayeur-Champex-Chamonix CCC®”), per la TDS ("Sur les Traces des Ducs de Savoie") e per OCC 2021. *LAGO MAGGIORE INTERNATIONAL mini TRAIL (LMIminiT) 20 Km con 1.430 m D+; - Valore ITRA 1, per la CCC (“Courmayeur-Champex-Chamonix CCC®”), per la TDS ("SurlesTracesdesDucs de Savoie") e per OCC 2021. 2 - PREMI Non sono previsti premi in denaro. I premi sono cumulabili. Sono assegnati premi in natura/accessori tecnici/abbigliamento tecnico/coppe. Al termine della gara vengono comunque redatte le classifiche generali con i tempi di arrivo e pubblicate sul sito WWW.LMIT.INFO. Le uniche categorie sono “uomini” e “donne”. Verranno premiati: - I primi 10 uomini e le prime 10 donne assoluti dei due Trail (a prescindere da qualunque tipo di tesseramento); - Il primo uomo e la prima donna assoluti di ogni categoria di entrambe le gare; - La donna e l’uomo più anziani della manifestazione.