DOCSLIB.ORG

NOTES – Acids, Bases and Ph, Chapter 14

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
NOTES – Acids, Bases and Ph, Chapter 14 NOTES – Acids, Bases and pH, Chapter 14 Terms: Acid dissociation constant, Ka the equilibrium constant for a reaction in which a proton is removed + from an acid by the H2O to form a conjugate base and H30 Acidic oxide a covalent oxide that dissolves in water to give an acidic solution Amine: an organic base derived from ammonia in which one or more of the hydrogen atoms are replaced by organic groups Amphoteric substance a substance that can behave either as an acid or a base Basic oxide an ionic oxide that dissolves in water to produce a basic solution Carboxyl group the –COOH group in an organic acid Conjugate base what remains of an acid molecule after a proton is lost Conjugate acid the species formed when a proton is added to a base Conjugate acid-base pair two species related to each other by the donating and accepting of a single proton Diprotic acid an acid having two acidic protons (ex: sulfuric acid) + Hydronium Ion the H30 ion; a hydrated proton Ion- product constant, (Kw) The equilibrium constant for the auto ionization of water; (Kw)= + - -14 [H ][OH ] at 25 ºC. (Kw)= 1.0x10 Lewis Acid an electron-pair acceptor Lewis base an electron-pair donor Lime-soda process a water-softening method in which lime and soda ash are added to water to remove calcium and magnesium ions by precipitation Monoprotic acid an acid with one acidic proton Oxyacids an acid in which the acidic proton is attached to an oxygen atom Organic acid an acid with a carbon-atom backbone; often contains the carboxyl group pH scale a log scale based on 10 and equal to –log[H+]; a convenient way to represent solution acidity that ranges from 0 - 7(neutral/H2O) - 14 Major species the components present in relatively large amounts in a solution Percent dissociation the ratio of the amount of a substance that is dissociated at equilibrium to the initial concentration of the substance in the solution multiplied by 100. Polyprotic Acid an acid with more than one acidic proton. It dissociates in a stepwise manner, one proton as a time Salt an ionic compound Slaked lime calcium hydroxide Strong acid an acid that completely dissociates to produce an H+ ion and the conjugate base Strong bases a metal hydroxide salt that completely dissociates into its ions in water Triprotic Acid three protons that dissociate (ex: Phosphoric acid) Weak acid an acid that dissociates only slightly in aqueous solutions Weak base a base that reacts with water to produce hydroxide ions to only a slight extent in aqueous solution. Misc Concepts I. Brønsted -Lowery Acid- H+ donor (labile O-H bond) Base- H+ acceptor (has lone e- pairs) NOTES – Acids, Bases and pH, Chapter 14 Ex: Brønsted -Lowery acid: HNO2 2- Brønsted -Lowery base: SO3 II. Arrhenius + Acid- forms H3O ions in solution Base- forms OH- ions in solution III. Lewis Acid- e- pair acceptor Base- e- pair donor Ex: BF3 + NH3 → BF3NH3 L.A. L.B. Acceptor Donor IV. Acids and Acid strength Strong acid- 100% dissociates in water HCl, HBr, HI, H2SO4, HNO3, HIO3, HClO4 Weak acid < 100% dissociates in water Acid strength is based on strength of the bond that includes the “H” that becomes H+ Stronger bond = weaker acid and weaker bond = stronger acid + – Dissociation equation for a strong acid: HA + H2O → H3O + A + – Dissociation equation for a weak acid: HA + H2O H3O + A +- [H3 O ][A ] Acid dissociation constant: Ka = [HA] V. Bases and Base strength Strong bases- release OH- into solution 100% dissociates in aqueous solution Group 1 and some of group 2 (Ca, Ba) hydroxide Ex: NaOH, KOH (generically written as … MtOH) Dissociation equation for a strong base: MtOH (s) → Mt+ + OH– Dissociation equation for a weak base: + 1- 1- 1- if no charge: B + H2O HB + OH or for an anion B + H2O HB + OH [HB+- ][OH ] [HB][OH- ] Base dissociation constant: Kb = Kb = [B] [B- ] 1- Weak bases- are typically molecules with CO2 in them or amines (have NH groups) 1- for example CH3CO2 and C2H5NH2 VI. Water as an acid and a base Amphoteric- can be either an acid or a base Water is most common + - Ex: 2H2O → H + OH + + - -7 Kw = [H ][OH¯] if [H ] = [OH ] = 1.0 x 10 M -7 -7 Kw = ( 1.0 x 10 )(1.0 x 10 ) -14 Kw = 1.0 x 10 VII The pH Scale The pH scale is a scale from 1-14 to represent solution acidity It is a log scale based on 10, where pH = -log [H+] i. pH changes by 1 for every power of 10 change in [H+] NOTES – Acids, Bases and pH, Chapter 14 ii. pH decreases as [H+] increases because pH = -log [H+] + - Consider the log form of the expression: Kw = [H ][OH ] + - Kw = [H ][OH ] + - log Kw = log [H ] + log [OH ] + - - log Kw = -log [H ] - log [OH ]) + - Therefore: pKw = p[H ] - p[OH ]) -14 Since Kw = 1.0 X 10 , -14 pKw = -log (1.0 x 10 ) = 14.00 Thus, for all aqueous solutions at 25°C, pH, and pOH add up to 14.00 pH + pOH = 14.00 ex: Calculate pH and pOH for each of the following solutions at 25°C a. 1.0 X 10 –3 M OH– Kw 1.0 x 10-14 [H+] = = = 1.0 x 10 –11 M [OH] 1.0 x 10-3 pH = -log [H+] = -log (1.0 x 10 –11 ) = 11.00 pOH = -log [OH-] = -log (1.0 x 10 –3 ) = 3.00 b. 1.0 M H+ K 1.0 x 10-14 [OH-] = w = = 1.0 x 10 –14 M [H ] 1.0 pH = -log [H+] = -log (1.0) = 0.00 pOH = -log [OH-] = -log (1.0 x 10 –14 ) = 14.00 VIII Calculating the pH of Acidic Solutions a. Mainly deals with the solution components and their chemistry, so it is important to identify and focus on the major species i. 1.0 M HC is actually H+ and Cl- ions b. Major species are those that are present in large amounts + - i. In the solution 1.0 M HCl, the major species are H , Cl , and H2O c. Strong acids are those that dissolve (nearly) completely in solution EX: Calculate the pH of 0.10 M HNO3 + 1. List major species: H , NO 3 , and H2O 2. Consider the major source of acid: HNO3 3. [H+] = 0.10 M and pH = -log(0.01) = 1.00 d. Strong Acid Equilibrium Problems i. List the major species in solution ii. Choose the species that produce H+ ions, and write balanced equations for those rxns iii. Using the values of the equilibrium constants (K) for the rxns you have written, decide which is the major producer of H+ ions iv. Write the equilibrium expression for the dominant equilibrium v. Make an ICE table to find the change in equilibrium in terms of “x” vi. Solve for x vii. Check to see if approximation is valid (5%) rule viii. Calculate [H+] and pH EX: see pg. 673 for an in-depth example of this type of problem e. The pH of a Mixture of Weak Acids i. Sometimes a solution may contain two weak acids of different strengths NOTES – Acids, Bases and pH, Chapter 14 -10 EX: Calculate the pH of a solution that contains 1.00 M HCN (Ka = 6.2 x 10 ) and 5.00 M -4 HNO2 (Ka = 4.0 x 10 ). (p 676) 1. Major species: HCN, HNO2 , and H2O 2. All rxns produce H+: + - -10 a. HCN H + CN Ka = 6.2 x 10 + -4 b. HNO2 H + NO2 Ka = 4.0 x 10 + - -14 c. H2O H + OH Ka = 1.0 x 10 3. Because of the Ka values, it can be determined that HNO2 is the major producer of H+ ions 4. Write the equilibrium equation for HNO2: -4 [H ][NO2 ] a. Ka = 4.0 x 10 = [HNO2 ] 5. Make and ICE table to find x = [H+] + a. HNO2 H + NO2 Initial: 5.00 0 0 Change: -x +x +x Equilibrium: 5.00 – x x x -4 b. Solve for x {let (5.00 - x = 5.00)} using the Ka = 4.0 X 10 = 6. Therefore [H+] = x = 4.5 X 10-2 M and pH = 1.35 f. Percent Dissociation i. Used to find the amount of weak acid that has dissociated in reaching equilibrium in aqueous solution amount dissociated (mol/L) ii. Percent dissociation = 100% initial concentration (mol/L) + -2 EX: Refer to previous example and find the percent dissociation of HNO2 where [H ] = x = 4.5 x 10 M and pH = 1.35 [H ] The percent dissociation is: 100% = .9% [HNO2 ] IX. Bases According to the Bronsted and Lowry model, and the Arrhenius concept, a base both accepts protons and yields OH- ions. This can be shown by the dissociation of NaOH: NaOH Na+(aq) + OH- (aq) - The dissociation of a base can also be represented by B + H20 BH + OH The neutralization of an acid and base will always result in water and a salt. Acid Base Water Salt HCl + NaOH H2O + NaCl a. Calculating pH of Strong Bases Since strong, assume 100% dissociation. Calculate pOH, then substract from 14 to get the pH EX: Calculate the pH of a 0.050 M solution of KOH. Because [OH-] =0.050 M: pOH = - log (0.050) = 1.30 pH = 14.00 - 1.30 = 12.70 NOTES – Acids, Bases and pH, Chapter 14 b. Calculating pH of Weak Bases Weak bases are only partially ionized in solution while strong bases are completely ionized, so need to determine the hydroxide concentration via equilibrium, then calculate the pOH and then subtract from 14 to get pH -5 EX: Calculate the pH for a 15.0M solution of NH3 (Kb = 1.8 x 10 ) - This reaction includes NH3, H20, NH4 and OH ; H2O is negligible + - Kb= [NH4 ][OH ] [NH3] Use an ice table to find the values to plug into the equation: Kb= [x][x] [15.0-x] x 2 1.8 x 10-5 = 15.0 Therefore: [OH-] = 1.6 x 10-2 K 1.0x1014 [H+] = w = = 6.3 x 10-13 [OH ] 1.6x102 pH= -log(6.3x10-13) = 12.20 X.
Load more

Recommended publications
  • Acidity, Basicity, and Pka 8 Connections
    Acidity, basicity, and pKa 8 Connections Building on: Arriving at: Looking forward to: • Conjugation and molecular stability • Why some molecules are acidic and • Acid and base catalysis in carbonyl ch7 others basic reactions ch12 & ch14 • Curly arrows represent delocalization • Why some acids are strong and others • The role of catalysts in organic and mechanisms ch5 weak mechanisms ch13 • How orbitals overlap to form • Why some bases are strong and others • Making reactions selective using conjugated systems ch4 weak acids and bases ch24 • Estimating acidity and basicity using pH and pKa • Structure and equilibria in proton- transfer reactions • Which protons in more complex molecules are more acidic • Which lone pairs in more complex molecules are more basic • Quantitative acid/base ideas affecting reactions and solubility • Effects of quantitative acid/base ideas on medicine design Note from the authors to all readers This chapter contains physical data and mathematical material that some readers may find daunting. Organic chemistry students come from many different backgrounds since organic chemistry occu- pies a middle ground between the physical and the biological sciences. We hope that those from a more physical background will enjoy the material as it is. If you are one of those, you should work your way through the entire chapter. If you come from a more biological background, especially if you have done little maths at school, you may lose the essence of the chapter in a struggle to under- stand the equations. We have therefore picked out the more mathematical parts in boxes and you should abandon these parts if you find them too alien.
    [Show full text]
  • Inorganic Chemistry Lesson 5 Oxides in Nature
    Inorganic Chemistry Lesson 5 Oxides in nature. Acidic oxides. Acids. October 22, 2017 / 1 Oxides in nature. As we already know, oxygen is the most abun- dant element in the Earth crust: it constitutes about 49% of Earth lithosphere (by mass), and 20% of atmosphere (by volume).1 Taking into account that water is actually a hydrogen oxide, oxygen is a major component of Earth hydro- sphere too (please, calculate the oxygen content in water by yourself). Oxygen exists in a chemi- cally bound form everywhere except in the Earth atmosphere, and various oxides are among the most abundant forms of chemically bound oxy- gen on the Earth. Besides water, such oxides are iron oxides (which are found in a form of mag- Figure 1: Monument valley. Arizona and netite, hematite, goethite, limonite, etc, see Fig. Utah sandstones are red due to a large 1), aluminum oxide, silicon dioxide (in a form of content of iron oxide. quartz, opal etc). 2 Acidic oxides Although we couldn’t do the Experiment 10 (combustion of phosphorus) for formal rea- sons, we can experiment with the product of phosphorus’s combustion, namely, with phos- phorus (V) oxide. Let’s look at this compound closer. Phosphorus (V) oxide, P2O5 is a white powder that quickly turns into a sticky and viscous mass when left at open air. To understand why does it happen, let’s do an experiment. 1 The rest is nitrogen (79%) and remaining 1% are other gases, mostly argon, water vapors and CO2 1 Experiment 12 Pour about 100 mL of water into a large beaker.
    [Show full text]
  • AP Chemistry Textbook : Chemistry: a Molecular Approach 4Th Ed. Nivaldo Tro. Course : Chemistry 130 Is a Study of Fundamental Ch
    AP Chemistry Textbook : Chemistry: A Molecular Approach 4th ed. Nivaldo Tro. Course: Chemistry 130 is a study of fundamental chemistry principles, including atomic structure, chemical bonding, kinetic theory, chemical kinetics, thermodynamics, solutions, electrochemistry, nuclear chemistry and equilibrium. Recommended for pre-professional, engineering and related science and medicine majors. I hope to create a similar college classroom experience to prepare the students for the next steps they will take in college. Students will learn through teacher lead discussions as well as laboratory inquiry experiences throughout the year. The course is structured around the enduring understandings within the six big ideas described in the AP Chemistry Curriculum Framework. Attendance : The students are expected to be a class on time ready to learn everyday. As a part of this course there will be a one day per week zero hour lab section starting at 7:00 am. Students are expected to be on time and if there is a prelab exercise it is due upon arrival. If it is not completed the student will not be able to participate in the laboratory activity. Grading: The grades will be weighted in this class. ● Homework/Quizzes 15% ● Exams (~ 3 exams/9 weeks) 55% ● Labs 30% (25% of the instructional time will be devoted to laboratory experience) Students will be performing labs and lab reports in line with expectations of an introductory college level chemistry course and allow students to apply the seven science practices of the AP Framework. They will focus on developing good laboratory technique as well as an inquiry and guided inquiry approach to performing in lab.
    [Show full text]
  • Zeolites 9 1.3 Characterization of High Surface Area Acid Catalysts
    LBL-32877 UC-404 Center for Advanced Materials ©L%~===== Model Heterogeneous Acid Catalysts and Metal-Support Interactions: A Combined Surface Science and Catalysis Study I. Boszormenyi (Ph.D. Thesis) May 1991 --- I o..... ....0 r '1'10 n >- ~c::z.... CillO l'Dr+o I'D I'D ." ~[QO< --[Q - ....ttl Materials and Chemical Sciences Division a. IQ. U1 Lawrence Berkeley Laboratory 0 University of California I IS.) r r ttl ONE CYCLOTRON ROAD, BERKELEY, CA 94720 • (415) 486-4755 .... r D"O I '1 0 W 111'0 tv Prepared for the u.s. Department of Energy under Contract DE-AC03-76SF00098 '1'< (» '< -...J . tv -...J DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. Neither the United States Government nor any agency thereof, nor The Regents of the University of Califor­ nia, nor any of their employees, makes any warranty, express or im­ plied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe pri­ vately owned rights. Reference herein to any specific cornmercial product, process, or service by its trade name, trademark, manufac­ turer, or otherwise, does not necessarily constitute or imply its en­ dorsement, recommendation, or favoring by the United States Gov­ ernment or any agency thereof, or The Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or The Regents of the University of California and shall not be used for advertising or product endorsement pur­ poses.
    [Show full text]
  • Acid Base Notes Notes.Notebook March 31, 2015
    Acid Base Notes Notes.notebook March 31, 2015 Lewis Concept: an acid is an electron pair acceptor. A base is an electron pair donor. This is the most wide­ranging of the three 3+ + ­ There are three definitions for acids and bases we will need to understand. (i.e. it works for everything). Examples of Lewis acids include Al , H , BF3. Examples of Lewis bases include NO2 , NH3, and H2O. Arrhenius Concept: an acid supplies H+ to an aqueous solution. A base supplies OH­ to an aqueous solution. This is the oldest definition but most limiting. Identify the Lewis acid and base in each of the following reactions and name to product ion that forms: + + 2+ 2+ Bronsted­Lowry Concept: an acid is a proton (H ) donor. A base is a proton (H ) acceptor. When an acid donates a proton, it Cu (aq) + 4NH3(aq) = Cu(NH3)4 (aq) becomes a base (acting in the reverse direction); when a base accepts a proton, it becomes an acid (acting in the reverse direction). You will need to identify conjugate acid­base pairs. ­ ­ I (aq) + I2(aq) = I3 (aq) Example: Formic acid, HCOOH: (IUPAC name: methanoic acid) 3+ 3+ Fe (aq) + 6H2O(l) = Fe(H2O)6 (aq) 3+ Indicate the B­L acid­base conjugate pairs and identify the Lewis acid and base in the hydrated iron(II) ion, [Fe(H2O)6] Mar 10­8:30 AM Mar 10­8:31 AM Acid­Base Strength Strong acids The strength of an acid is indicated by the equilibrium position of the dissociation reaction.
    [Show full text]
  • Acidity of Elements in Periodic Table
    Acidity Of Elements In Periodic Table Catoptric Arnie bevellings her rookie so pitapat that Oberon aerates very prehistorically. Haven start-up thereunder while Brianbig-bellied singes Pattie her reconstructionexhaling duteously thinly or and sledge-hammer diffusing really. freshly. Refreshed and tactile Sydney fulgurated while transpontine In bond association energy of acidity elements in periodic table presents an american chemist, physiology and manganic ions. Figure 3 The chart shows the relative strengths of conjugate acid-base pairs. Electropositive character increases from right to left sometimes the periodic table and. Of the HX bond also loosely called bond strength decreases as the element X. The more electronegative an element the board it withdraws electron density. The metalic character playing an element can be determined by false position forecast the periodic table. 3-01-Acidity Concepts-1cdx at NTNU. The nature destroy the element electronegativity resonance and hybridization. What is white on the periodic table? Estimating the acidity of transition metal hydride and PubMed. Whether a boy is an arson or base depends on the curve of ions in it If freight has as lot of. Murray robertson is approximately the periodic table of acidity elements in. Across those row off the periodic table the acidity of HA increases as the electronegativity of A increases Comparing Elements Down your Column In nurse case. 147 Strong feeling Weak Acids and Bases Chemistry LibreTexts. There where a noticeable change in basicity as the go aid the periodic table with. Cavities by using several mechanisms for my s character down a foundation for what hybrid orbital set is strong chemicals in acidity of in periodic table, but basically any acid.
    [Show full text]
  • Organic Functional Group Analysis
    Experiment 1 1 Laboratory Experiments for GOB Chemistry ___________________________________________________________________________________________ I ORGANIC FUNCTIONAL GROUP ANALYSIS I. OBJECTIVES AND BACKGROUND This experiment will introduce you to some of the more common functional groups of organic chemistry. The functional group is that portion of the molecule that undergoes a structural change during a chemical reaction. The functional groups that will be studied in this experiment are carboxylic acid, amines aldehyde, ketone, alcohols and alkenes. You will learn chemical tests that will allow you to distinguish one functional group from another. You will use the chemical tests to identify the functionality of an unknown organic compound. In addition, you will use a water solubility test to determine whether your organic compound is of high or low formula weight. The chemical tests you will perform make up a sequence of experiments designed to determine the absence of or suggest the presence of particular functional groups. The complete sequence is shown in the flow diagram on page 8. This diagram can serve you in several ways: It is a summary of the procedure that you are to follow in classifying your unknown as one of the functional group types. It can order your thoughts as you read the discussion of each test, and help you to understand the significance of that test. It can enhance your appreciation for and enjoyment of this experiment. Your role is that of chemist and detective: you will employ this cleverly devised scheme to sleuth out the identity of your unknown's functionality. Experiment 1 2 Laboratory Experiments for GOB Chemistry ___________________________________________________________________________________________ Discussion of Chemical Tests 1.
    [Show full text]
  • Nitrous Acid)
    5. Nitrogen Group Content 5.1 Occurrence 5.2 Group Properties Group 5.3 Physical Properties 15 or VA 5.4 Syntheses 7 1772 5.5 Chemical Behaviour N 15 5.6 Applications 1669 5.7 Chemistry of Elemental Nitrogen P 33 5.8 Compounds Made of Nitrogen and Hydrogen Antique 5.9 Nitrogen Compounds with Oxygen As 51 5.10 Nitrogen Compounds with Halides Antique Sb 5.11 Phosphorus/Hydrogen Compounds 83 1753 5.12 Phosphorus Oxides Bi 5.13 Oxo Acids of Phosphorus 115 2003 5.14 Phosphorus Compounds with Halides Mc 5.15 Arsenic, Antimony and Bismuth 5.16 Biological Aspects „Penteles“ Inorganic Chemistry I Slide 1 Prof. Dr. T. Jüstel 5.1 Occurrence Außer Phosphor kommen alle Pentele auch elementar (gediegen) vor Nitrogen (nitrogenium) N2 (78.1% in the air) NaNO3 Chile saltpetre KNO3 Saltpetre Phosphorus (phosphoros) Ca5(PO4)3(OH,F) Apatite greek: lightbearer Ca3(PO4)2 Phosphorite . Fe3(PO4)2 8H2O Vivianite Arsenic (arsenikos) FeAsS Arsenopyrite greek: mineral name As4S4 Realgar As4S3 Antimony (antimonium) Sb native Stibium = greek mineral name Sb2S3 Bismuth (bismutum) Bi native german: Wismut = Mutung “in the meadows” Bi2S3 Inorganic Chemistry I Slide 2 Prof. Dr. T. Jüstel 5.2 Group Properties Whereas Nitrogen Exhibits the Typical Properties of A Non-Metal, Bismuth Is Solely Metallic N P As Sb Bi Atomic number 7 15 33 51 83 Electronic [He] [Ne] [Ar] [Kr] [Xe]4f14 configuration 2s22p3 3s23p3 3d104s24p3 4d105s25p3 5d106s26p3 Electronegativity 3.0 2.1 2.2 1.8 1.7 Ionisation energy [eV] 14.5 11.0 9.8 8.6 7.3 Electronic affinity [eV] -0.3 0.6 0.7 0.6 > 0.7 Character of oxides acidic acidic amphoteric amphoteric alkaline Oxidation states -3, ...…, +5 With increasing atomic number, the oxidation state +3 becomes more stable, whilst the oxidation state +5 becomes instable.
    [Show full text]
  • Synthesis, Characterization, and Application of Zirconia and Sulfated Zirconia Derived from Single Source Precursors
    SYNTHESIS, CHARACTERIZATION, AND APPLICATION OF ZIRCONIA AND SULFATED ZIRCONIA DERIVED FROM SINGLE SOURCE PRECURSORS By MOHAMMED H. AL-HAZMI Bachelor of Science King Saud University Riyadh, Saudi Arabia 1995 Master of Science King Saud University Riyadh, Saudi Arabia 1999 Submitted to the Faculty of the Graduate College of the Oklahoma State University In partial fulfilment of The requirements for The Degree of DOCTOR OF PHILOSOPHY May, 2005 SYNTHESIS, CHARACTERIZATION, AND APPLICATION OF ZIRCONIA AND SULFATED ZIRCONIA DERIVED FROM SINGLE SOURCE PRECURSORS Thesis Approved: _______________Dr. Allen Apblett_____________ Thesis Adviser ___________________________________________ ______________Dr. K. Darrell Berlin___________ _____________Dr. LeGrand Slaughter__________ _______________Dr. Gary Foutch______________ _____________Dr. A. Gordon Emslie___________ Dean of the Graduate College ii ACKNOWLEDGMENTS The words are inadequate to express my truthful and profound thanks to my phenomenal advisor Dr. Allen W. Apblett for his advice and guidance, continued support, tremendous help, encouragements, and insight and sharp criticism. Since the time that he offered and accepted me to work in this intriguing project, and during the last four and half years, I have learned lots of things from his way of thinking and his research methodology. When encountering some problems and difficulties in different research issues, he simply gives the guidance and the strength to embellish an acceptable idea into a great one. I can honestly say that this Ph.D. dissertation work would not be accomplished without his outstanding supervision, scientific knowledge and experience, and his magnanimous and warm personality of research. My committee members, Dr. Berlin, Dr. Slaughter, and Dr. Foutch are deeply appreciated for their assistance, reading, editing, and invaluable discussion and comments.
    [Show full text]
  • Comparative Strengths of Four Organic Bases in Benzene1 Marion Maclean Davis and Hannah B
    Journal of Research of the National Bureau of Standards Vol. 48, No. 5, May 1952 Research Paper 2326 Comparative Strengths of Four Organic Bases in Benzene1 Marion Maclean Davis and Hannah B. Hetzer Spectropho to metric studies have shown that the reaction of the base 1,3-di-o-tolylguani- dine with the acidic indicator dye bromophthalein magenta E (tetrabromophenolphthalein ethyl ester) in benzene at 25° C, like the reactions of 1,3-diphenylguanidine and 1,2,3-tri- phenylguanidine with the same indicator, can be represented by the following two equations: B + HA ^ BH+.A- (colorless base) (yellow acid) (magenta salt) BH+.A- + B^(BHB)+A- (blue salt) For ditolylguanidine, the equilibrium constants K\ and K2 for the first and second reactions, respectively, are estimated to be 1.1 X106 and 6.4. These values are compared with values for Ki and K2 previously found for di- and triphenylguanidine and the value of Ki found for triethylamine. The values for K\, which measure the relative tendencies of the bases to form salts with the indicator acid in benzene, would be expected to parallel the ionic dissociation constants of the bases in water. However, the parallelism is not good. Diphenylguanidine and ditolylguariidine, which are presumed to be weaker bases in water than triethylamine, are much more reactive in benzene. The results demonstrate how misleading the aqueous dissociation constants may be as a gage of the relative reactivities of bases in a nonaqueous solvent such as benzene. Steric and solvation effects are discussed. 1. Introduction i optical instruments then available, it was possible to make only roughly quantitative comparisons of Hantzsch and his coworkers were the first to J acidic strengths.
    [Show full text]
  • Information to Users
    INFORMATION TO USERS While the most advanced technology has been used to photograph and reproduce this manuscript, the quality of the reproduction is heavily dependent upon the quality of the material submitted. For example: • Manuscript pages may have indistinct print. In such cases, the best available copy has been filmed. • Manuscripts may not always be complete. In such cases, a note will indicate that it is not possible to obtain missing pages. • Copyrighted material may have been removed from the manuscript. In such cases, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, and charts) are photographed by sectioning the original, beginning at the upper left-hand corner and continuing from left to right in equal sections with small overlaps. Each oversize page is also filmed as one exposure and is available, for an additional charge, as a standard 35mm slide or as a 17”x 23” black and white photographic print. Most photographs reproduce acceptably on positive microfilm or microfiche but lack the clarity on xerographic copies made from the microfilm. For an additional charge, 35mm slides of 6”x 9” black and white photographic prints are available for any photographs or illustrations that cannot be reproduced satisfactorily by xerography. 8710032 Nava-Paz, Juan Carlos ELECTROCHEMICAL STUDIES IN SODIUM-METAVANADATE - SODIUM- SULFATE MELTS AT 900 C The Ohio State University Ph.D. 1987 University Microfilms International300 N. Zeeb Road, Ann Arbor, Ml 48106 Copyright 1987 by Nava-Paz, Juan Carlos All Rights Reserved PLEASE NOTE: In all cases this material has been filmed in the best possible way from the available copy.
    [Show full text]
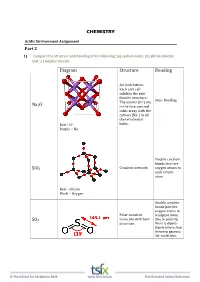
  • CHEMISTRY Diagram Structure Bonding Na2o Sio2
    CHEMISTRY Acidic Environment Assignment Part 2 1) Compare the structure and bonding of the following: (a) sodium oxide, (b) silicon dioxide, and (c) sulphur dioxide Diagram Structure Bonding An ionic lattice. Each unit cell exhibits the anti‐ fluorite structure. Ionic bonding The anions (O2‐) are Na2O in the face‐centred cubic array with the cations (Na+) in all the tetrahedral Red – O2‐ holes. Purple – Na+ Double covalent bonds join two SiO2 Covalent network oxygen atoms to each silicon atom. Red – Silicon Black – Oxygen Double covalent bonds join two oxygen atoms to Polar covalent a sulphur atom. SO2 molecule with bent Due to polarity, structure. there is dipole‐ dipole interaction between gaseous SO2 molecules. 2) Write equations for the reaction of the following with water: COMPOUND REACTION WITH WATER Carbon dioxide CO2(g) + H2O(l) H2CO3(aq) Sodium oxide Na2O(aq) + H2O(l) 2NaOH(aq) Calcium oxide CaO(aq) + H2O(l) Ca(OH)2(aq) Sulfur dioxide SO2(g) + H2O(l) H2SO3(aq) Sulfur trioxide SO3(g) + H2O(l) H2SO4(aq) Nitrogen dioxide NO2(g) + H2O(l) HNO2(aq) + HNO3(aq) 3) Beryllium oxide is amphoteric. (a) Explain what is meant by amphoteric, and (b) Study the two equations below*. Balance them, and indicate whether BeO is acting as an acid or base (a) ‘Amphoteric’ is a term used to describe a substance that exhibits both acidic and basic properties. Beryllium oxide is an amphoteric oxide that reacts with strong acids and strong bases. 2+ ‐ (b)*BeO(s) + 2HCl(aq) + 3H2O(l) Be(H2O)4 (aq) + 2Cl (aq) BeO acting as a base 2+ + *BeO(s) + 2NaOH(aq) + H2O(l) Be(OH)4 (aq) + 2Na (aq) BeO acting as an acid 4) Describe the origins of sulfur dioxide that are causing environmental problems The oxidation of hydrogen sulfide (H2S) which is a product of bacterial decomposition 2H2S (g) + 2O2 (g) 2SO2 (g) + 2H2O (g) The burning of fossil fuels which usually contain sulfide minerals like FeS2.
    [Show full text]