DOCSLIB.ORG

Optimization of Thruster Allocation for Dynamically Positioned Marine Vessels

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optimization of Thruster Allocation for Dynamically Positioned Marine Vessels UNIVERSITY OF RIJEKA FACULTY OF ENGINEERING Department of Naval Architecture and Ocean Engineering Marko Valčić OPTIMIZATION OF THRUSTER ALLOCATION FOR DYNAMICALLY POSITIONED MARINE VESSELS DOCTORAL THESIS Rijeka, 2020 UNIVERSITY OF RIJEKA FACULTY OF ENGINEERING Department of Naval Architecture and Ocean Engineering Marko Valčić OPTIMIZATION OF THRUSTER ALLOCATION FOR DYNAMICALLY POSITIONED MARINE VESSELS DOCTORAL THESIS Supervisor: Prof. D. Sc. Jasna Prpić-Oršić Rijeka, 2020 SVEUČILIŠTE U RIJECI TEHNIČKI FAKULTET Zavod za brodogradnju i inženjerstvo morske tehnologije Marko Valčić OPTIMIZACIJA ALOKACIJE PROPULZORA KOD DINAMIČKI POZICIONIRANIH PLOVNIH OBJEKATA DOKTORSKI RAD Mentorica: prof. dr. sc. Jasna Prpić-Oršić Rijeka, 2020. Thesis Supervisor: Prof. D. Sc. Jasna Prpić-Oršić University of Rijeka, Faculty of Engineering, Rijeka, Croatia This doctoral thesis was defended on 6 March 2020 at the University of Rijeka, Faculty of Engineering, Rijeka, Croatia, in front of the following Evaluation Committee: 1 Prof. D. Sc. Roko Dejhalla, Chairman of the Committee University of Rijeka, Faculty of Engineering, Rijeka, Croatia 2 Prof. D. Sc. Senka Maćešić, Member of the Committee University of Rijeka, Faculty of Engineering, Rijeka, Croatia 3 Prof. D. Sc. Nastia Degiuli, Member of the Committee University of Zagreb, Faculty of Mechanical Engineering and Naval Architecture, Zagreb, Croatia Dedicated to my parents, Dora and Šime. "Truth is much too complicated to allow anything but approximations." John von Neumann Acknowledgments This work has been supported in part by the Croatian Science Foundation under the projects HRZZ-IP-2013-11-8722 (Greener Approach to Ship Design and Optimal Route Planning) and HRZZ-IP-2018-01-3739 (Decision Support System for Green and Safe Ship Routing). This work has also been supported in part by the University of Rijeka under the projects uniri-tehnic-18-266 (The impact of environmental loads on the characteristics of dynamic positioning systems for marine vessels) and uniri-tehnic-18-18 (Uncertainties of ship speed loss evaluation under real weather conditions), and by the University of Rijeka, Faculty of Engineering, Rijeka, Croatia. During this PhD Study, I was fortunate enough to interact and discuss with a number of researchers from whom I have benefited substantially. Therefore, I would like to express my appreciation to all of them who have offered their time, advice, assistance, support and encouragement. Most of all I would like to thank my supervisor, Professor Jasna Prpić-Oršić from the Faculty of Engineering, University of Rijeka, Rijeka, Croatia, for taking me in as a PhD Candidate, for believing in me, and for being such a great advisor and a great friend during all these years. Your encouragement and support were the key to solving every single problem or obstacle that came up during this research. Special thanks also goes to Professor Radoslav Nabergoj from the Faculty of Engineering, University of Trieste, Trieste, Italy, for the motivation received to accomplish this work and for lots of valuable discussions about initial key ideas related to dynamic positioning and thruster interactions. Particularly motivating periods during this PhD study were my research visits to the Centre for Autonomous Marine Operations and Systems (AMOS), Department of Marine Technology, Norwegian University of Science and Technology (NTNU), Trondheim, Norway, from 2015 to 2017. Hence, I would like to express my sincere gratitude to my hosts, Professor Odd M. Faltinsen, Scientific advisor of AMOS, Professor Asgeir J. Sørensen, Director of AMOS, and Professor Sverre Steen, Head of Department of Marine Technology. Special thanks goes to Professor Sverre Steen and his former MSc student Mikal H. Espedal, for very valuable discussions on the thruster-thruster interactions and for providing me great support in extending the thruster-thruster interaction model based on the results of Mr. Erik Lehn, to whom I am also very grateful. Due to the limited space, it is not quite possible to mention all the people I would still like to thank. However, at least I can say a sincere thanks to all my dear professors, colleagues and friends from the University of Rijeka, Faculty of Maritime Studies and Faculty of Engineering, for their great support and friendship. At last, but not least, I especially have to point out that my family has always been with me and supported me from the very beginning in every way possible. I thank them immensely for their love and support, because without them this kind of work would not be possible to complete. A special gratitude goes to my wife Sonja for all those years of understanding, encouragement and support. viii Abstract Existing strategies and proposed methods for optimal thruster allocation in dynamic positioning systems of marine vessels are primarily focused on minimization of power consumption with handling of numerous constraints and limitations that should be satisfied at the same time. This particularly applies to thruster saturation and forbidden zones that are usually used in order to avoid or reduce thrust losses due to thruster-thruster interactions. By defining a forbidden zone for an azimuth thruster, generally a non-convex thrust region is left over which consequently can cause the significant deviations in allocated thruster azimuth angles and increase the time required for thrust and azimuth angle allocation. On the other hand, one can notice that thruster interaction effects such as axial and transverse current, thruster-hull interaction, thruster-thruster interaction and ventilation are rarely taken into account. These effects, whether they occur separately or in combinations, can cause significant thrust losses, which without appropriate reallocation strategy would consequently lead to degradation of vessel position and heading, as well as to increase of response time and power consumption. In dynamic positioning systems, nonlinear objective functions, and nonlinear equality and inequality constraints within optimal thrust allocation procedures cannot be handled directly by means of the solvers like industry-standardized quadratic programing, at least not without appropriate linearization technique applied, which can be computationally very expensive. Thus, if optimization requirements are strict and problem should be solved for nonlinear objective function with nonlinear equality and inequality constraints, than one should use some appropriate nonlinear optimization technique. In addition, implementation of thruster interactions in optimal thrust allocation can easily transform the optimization problem into nonlinear and non-convex, which can become very demanding. In this context, two optimization approaches have been proposed. The first one is based on the weighted generalized inverse matrix approach, and the other one on the hybrid approach using sequential quadratic programing and direct search algorithms coupled with generalized regression neural network. The latter one is particularly convenient for handling non-convex and nonlinear optimization issues related to generally nonlinear power-thrust relationship and to non-convex nature of forbidden zones and thruster interaction effects. Moreover, both optimization approaches can handle selected thruster interaction effects with negligible increase in total power consumption, compared to the strategy based on forbidden zones only, while minimizing the tear and wear of thrusters at the same time. Obtained results were evaluated with numerous simulations involving different initial conditions and with direct comparison of analysed strategies that include forbidden zones, i.e. thruster-thruster interactions. Key words Dynamic positioning systems, thruster interactions, thrust losses, thruster allocation, nonlinear optimization ix Sažetak Postojeće strategije i predložene metode optimalne alokacije propulzora u sustavima za dinamičko pozicioniranje plovnih objekata su primarno usredotočene na minimizaciju potrošnje električne energije uz istovremeno zadovoljavanje brojnih ograničenja i uvjeta. To se posebno odnosi na zasićenje propulzora, kao i na zabranjene zone koje se uobičajeno koriste kako bi se izbjegli ili smanjili gubici poriva uzrokovani međudjelovanjem propulzora. Uvođenjem zabranjene zone za neki azimutni propulzor, skup mogućih rješenja tog propulzora općenito će postati ne-konveksan, što posljedično može rezultirati značajnim promjenama u alociranim azimutima te povećanjem vremena potrebnog za alokaciju propulzora. S druge strane, može se primijetiti da se učinci međudjelovanja propulzora poput aksijalnog i poprečnog sustrujanja, međudjelovanja propulzor-trup, međudjelovanja propulzor-propulzor i ventilacije, vrlo rijetko uzimaju u obzir. Ovi učinci, neovisno da li se javljaju svaki posebno ili u kombinacijama, mogu uzrokovati značajno smanjenje poriva, što bez odgovarajuće realokacijske strategije posljedično može dovesti do degradacije pozicije i smjera napredovanja plovnog objekta, te do povećanja vremena odziva i potrošnje električne energije. U sustavima za dinamičko pozicioniranje, nelinearne funkcije cilja te nelinearna ograničenja u obliku jednakosti i nejednakosti ne mogu se izravno uzeti u obzir u optimalnoj alokaciji poriva. Kod industrijski prihvaćene metode kvadratičnog programiranja potrebno je provesti odgovarajuću linearizaciju koja može cijelu optimizaciju učiniti vrlo zahtjevnom u računalnom smislu. Stoga, ukoliko su zahtjevi optimizacije strogi, i problem je potrebno riješiti za
Load more

Recommended publications
  • A Study of the Twin Fin Concept for Cruise Ship Applications
    Centre for Naval Architecture A Study of the Twin Fin Concept for Cruise Ship Applications Frida Nyström [email protected] Master of Science Thesis KTH Stockholm, Sweden June 2015 Abstract The aim with this thesis is to investigate if the Twin Fin concept can be a beneficial propulsion system for large cruise ships, about 300 m long. The Twin Fin concept is a new propulsion system, launched in 2014 by Caterpillar Propulsion [1]. The concept is diesel-electric and has two fins, containing a gearbox and an electric motor, immersed in water [2]. Previous investigations have shown the concept to have several advantages compared to other propulsion systems . A seismic vessel, Polarcus, has been retrofitted with the Twin Fin concept and it has been proved to have both operating and cost benefits compared to its previous arrangement with azimuth thrusters [3]. Diesel-electric propulsion is common for cruise ships, which would make the Twin Fin concept a possible propulsion solution for them. It’s of interest to investigate if the concept can be as beneficial for large cruise ship as it has shown to be for other vessel types. To investigate this the whole concept is considered. A cruise ship hull and fins are modeled with computer-aided design (CAD) using CAESES/FRIENDSHIP- Framework (CAESES/FFW), starting building up a procedure for customization of fin design into ship layout. Tracking of the operation of similar cruise ships is performed with automatic identification system (AIS) in order to create an operational profile for the model cruise ship. A propeller is designed for the model cruise ship, using a Caterpillar Propulsion in-house software.
    [Show full text]
  • Veth Rudder Propellers Toturn Yourworld the Power
    VETH RUDDER PROPELLERS TO TURN YOUR WORLD YOUR TURN TO THE POWER POWER THE BY About Veth Propulsion Veth Propulsion, by Twin Disc, is a customer-oriented Dutch thruster manufacturer. A family-owned company, established in Papendrecht in the Netherlands in 1951, and international player which is leading in quality, service, innovation and sustainability. Veth Propulsion develops and produces various types of Your requirements are our starting point to entering into a Z-drives, including retractable thrusters, Hybrid Drives, Swing relationship. Due of the wide range of products, combined Outs and deck mounted units. You can find the Veth Rudder with the expertise of our staff and our innovative designs, you propeller everywhere, from inland marine to tug and offshore can always expect a total concept. vessels. The type of Z-drive that best suits your needs, depends on factors such as the type of vessel you have and the desired You can also choose to have the drive line delivered with your maneuverability. It revolves around what you consider to be rudder propeller or thruster. As a leading Scania and Sisu Diesel important! dealer, Veth Propulsion delivers new and remanufactured propulsion engines (variable speed) and generator engines You can expect a personal and down-to-earth approach and a (set and variable speed). reliable image and brand awareness in several marine markets. Your sailing profile and specific needs form the basis for our Relying on our expertise and decades of experience, we can bespoke solutions including rudder propellers, bow thrusters, give you advice on the most suitable solution and possibilities.
    [Show full text]
  • DYNAMIC POSITIONING CONFERENCE October 10-11, 2017
    Author’s Name Name of the Paper Session DYNAMIC POSITIONING CONFERENCE October 10-11, 2017 Thrusters Influence of Thruster Response Time on DP Capability by Time-Domain Simulations D. Jürgens, M. Palm Voith Turbo, Heidenheim, Germany D. Jürgens, M. Palm Influence of Thruster Response Time on DP Capability Abstract Due to their simplicity static approaches are a commonly used method of assessing the DP capability of offshore vessels. These static approaches are essentially based on a balance of forces and moments caused by environmental conditions, as well as the thruster forces. The ensuing DP plots usually come up with unrealistically high application limits regarding admissible environmental conditions for a given operation. This phenomenon is due to the fact that important influencing factors are being neglected. One example is the assumption that the vessel is at rest and another one is the fact that the responsiveness of thrusters is not considered. With the Voith-Schneider-Propeller an alternative propulsion system for DP applications is available. It differs from conventional azimuth thrusters primarily because of its faster thrust variation and thrust change over zero position. Since static approaches completely ignore this factor, this paper intends to quantify the influences of the response time of a thruster on the wind envelope with the help of time-domain DP simulations and the ensuing capability plots. For this purpose comprehensive simulations have been carried out for an offshore support vessel while varying the dynamic thruster characteristics. Relevant assessments show that the response time has a significant influence on the DP capability and thus the operational window.
    [Show full text]
  • Construction of a Hardware-In-The-Loop Simulator for Azipod Control System Testing
    Markus Nylund Construction of a hardware-in-the-loop simulator for Azipod control system testing Thesis submitted for examination for the degree of Master of Science in Technology. Espoo 03.08.2016 Thesis supervisor: Prof. Seppo Ovaska Thesis advisor: D.Sc. (Tech.) Juha Orivuori Aalto-universitetet, PL 11000, 00076 AALTO www.aalto.fi Sammandrag av diplomarbete Författare Markus T. V. Nylund Titel Construction of a hardware-in-the-loop simulator for Azipod control system testing Examensprogram Utbildningsprogrammet för elektronik och elektroteknik Huvud-/biämne Elektronik med tillämpningar Kod S3007 Övervakare Prof. Seppo Ovaska Handledare TkD Juha Orivuori Datum 03.08.2016 Sidantal 9+90 Språk engelska Sammandrag Syftet med detta diplomarbete är att konstruera en simulator för Azipod® roderpropellern. Azipod® är ett varumärke av en roderpropeller med en elmotor som driver propellern. Hela roderenheten är belägen utanför fartygets skrov och det är möjligt att rotera roderpropellern obegränsat runt sin axel. Unikt för roderpropellrar är att drivkraften kan göras fullständigt elektriskt samt att roderpropellern är en dragande propeller till skillnad från tryckande konventionella propellrar. Dessa egenskaper ökar på ett fartygs energieffektivitet. Målet med arbetet är att bygga en (Azipod®) roderpropellersimulator och en tillhörande styrenhet som liknar fartygs styrenheter. Fokus för arbetet ligger på propulsionsstyrenheten. Simulatorn skall fungera liknande som den kommersiella produkten, men med mindre hårdvara. Fartygs styrkonsolpaneler samt alla nödvändiga mätinstrument virtualiseras. Ett extra program skapas för att möjliggöra stimulans för systemet för de virtualiserade mätinstrumenten. Detta program körs från en godtycklig dator som är uppkopplad till simulator nätverket. Simulering av Azipod® roderpropellern utförs av två sammankopplade motorer. Den ena motorn representerar en Azipod® rodermotor och den andra motorn belastar propulsionsmotorn.
    [Show full text]
  • Optimal Thrust Allocation Methods for Dynamic Positioning of Ships
    Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Optimal Thrust Allocation Methods for Dynamic Positioning of Ships A thesis submitted to the Delft Institute of Applied Mathematics in partial fulfillment of the requirements for the degree MASTER OF SCIENCE in APPLIED MATHEMATICS by CHRISTIAAN DE WIT Delft, the Netherlands July 2009 Copyright © 2009 by Christiaan de Wit. All rights reserved. MSc THESIS APPLIED MATHEMATICS “Optimal Thrust Allocation Methods for Dynamic Positioning of Ships” CHRISTIAAN DE WIT Delft University of Technology Daily supervisor Responsible professor Dr. J.W. van der Woude Prof. dr. K.I. Aardal Other thesis committee members M. Gachet, Ingenieur ENSTA Dr. R.J. Fokkink July 2009 Delft, the Netherlands Optimal Thrust Allocation Methods for Dynamic Positioning of Ships Christiaan de Wit July 2009 Environment from Abstract The first Dynamic Positioning (DP) systems emerged in the 1960’s from the need for deep water drilling by the offshore oil and gas industry, as conventional mooring systems, like a jack-up barge or an anchored rig, can only be used in shallow waters. GustoMSC has been developing DP drill ships since the early 1970’s and it is still one of their core businesses. DP systems automatically control the position and heading of a ship subjected to environmental and external forces, using its own actuators. The thrust allocator of a DP system is responsible for the thrust distribution over the actuators of the ship. Apart from minimizing the power consumption an ideal thrust allocator can also take other aspects into account, such as forbidden/spoil zones and thruster relations.
    [Show full text]
  • Extending Uptimes for Tugs with the Voith Schneider Propeller (VSP) Case Study SHIPBUILDING & EQUIPMENT PROPULSION & MANOEUVRING TECHNOLOGY
    voith.com Extending uptimes for tugs with the Voith Schneider Propeller (VSP) Case study SHIPBUILDING & EQUIPMENT PROPULSION & MANOEUVRING TECHNOLOGY Extending uptime for tugs SEAKEEPING BEHAVIOUR Rolling movements are often the limiting factor for tug operations in waves. However, the Voith Schneider Propeller (VSP) with its fast and dynamic thrust adjustment, enables efficient active roll stabilisation and dynamic positioning (DP). This opens up new opportunities to increase the efficiency of tug operations, write Dr Dirk Jürgens and Michael Palm from Germany’s Voith GmbH. Tug rolling motions are often the limiting factor in offshore applications. While the waves counter LNG carriers from an optimal direction – from bow or stern – tugs often have to operate un- der the worst beam wave conditions. At a moderate significant wave height of Hs = 1.9m, roll angles of up to 26.7° were measured [5], with significant implica- tions for crew welfare and productivity. The VWT or RAVE Tug is a well- heberrechtlich untersagt. proven design and the Carrousel Rave Tug (CRT) [6] offers scope to deploy active Voith Roll Stabilization (VRS). As a re- sult, roll movements can be reduced con- siderably, by as much as 70% on tugs. The basis for the VRS is the fast response of the VSP [7], [8]. This article explains the effect of VRS using calculations, model tests and cus- tomer feedback as examples. The conclu- sion is that through the targeted use of Figure 1: Voith Water Tractor, Forte, equipped with two Voith Schneider Propellers (VSP36EC) VRS to reduce roll, the operating times and the electronic Voith Roll Stabilization (VRS) Source for all images and figures: Voith of offshore tugs can be significantly ex- ugs must now work in bigger waves because today’s larger vessels require Tthem to make line connections ear- lier, particularly in areas where consider- able waves build up [1].
    [Show full text]
  • A Methodology to Select the Electric Propulsion System for Platform Supply Vessels (PSV)
    CRISTIAN ANDRÉS MORALES VÁSQUEZ A methodology to select the electric propulsion system for Platform Supply Vessels (PSV) Dissertation submitted to Escola Politécnica da Universidade de São Paulo to obtain the degree of Master of Science in Engineering. São Paulo 2014 CRISTIAN ANDRÉS MORALES VÁSQUEZ A methodology to select the electric propulsion system for Platform Supply Vessels (PSV) Dissertation submitted to Escola Politécnica da Universidade de São Paulo to obtain the degree of Master of Science in Engineering. Concentration Area: Naval Architecture and Ocean Engineering. Advisor: Prof. Dr. Helio Mitio Morishita São Paulo 2014 Este exemplar foi revisado e corrigido em relação à versão original, sob responsabilidade única do autor e com a anuência de seu orientador. São Paulo, 27 de maio de 2014. Assinatura do autor ____________________________ Assinatura do orientador _______________________ Catalogação-na-publicação Morales Vasquez, Cristian Andres A methodology to select the electric propulsion system for Platform Supply Vessels / C.A. Morales Vasquez. – versão corr. -- São Paulo, 2014. 246 p. Dissertação (Mestrado) – Escola Politécnica da Universidade de São Paulo. Departamento de Engenharia Naval e Oceânica. 1.Propulsão 2.Navios I. Universidade de São Paulo. Escola Politécnica. Departamento de Engenharia Naval e Oceânica II.t. This work is especially dedicated to my parents, Tuli Vásquez and Andrés Morales. ACKNOWLEDGMENTS I would like to express my most sincere gratitude to my advisor, Prof. Dr. Helio Mitio Morishita, for giving me the opportunity to develop my Master’s dissertation with his help and guidance, for his teachings about naval architecture and ocean engineering, for his patience and for his excellent support. Thank you very much professor.
    [Show full text]
  • Hybrid Propulsion
    Rotterdam Mainport University of Applied Sciences - RMU Hybrid Propulsion Electrical Installations Group members: Arie Meerkerk Simon Zaalberg Nicky de Wit Wilco van Wijk Henk Kievit Group Principal: Mr. Voesenek Group Managers: Mr. Van kluijven Mrs. Toemen 1 Contents Preface: .................................................................................................................................................... 4 Introduction: ............................................................................................................................................ 5 1. What is hybrid propulsion, and what types of hybrid propulsion exist? ............................................ 6 1.1 Azimuth thrusters .................................................................................................................... 6 1.1.1 Azipod/ Azipull: ................................................................................................................ 6 1.2 Diesel-electrical ............................................................................................................................. 7 1.3 Gas-electric .................................................................................................................................... 7 2. On what types of ships would hybrid propulsion actually be useful? ................................................. 8 2.1 Ship types ...................................................................................................................................... 8
    [Show full text]
  • Marine Products and Systems
    MARINE PRODUCTS AND SYSTEMS kongsberg.com Our technologies, products and systems are continually improving. For the latest information please go to www.km.kongsberg.com All information is subject to change without notice. Content Introduction 03 Ship design 05 Propulsion systems 25 Diesel and gas engines 35 PROPULSORS • Azimuth thrusters 49 • Propellers 61 • Waterjets 67 • Tunnel thrusters 75 • Promas 81 • Podded propulsors 87 Reduction gears 97 STABILISATION AND MANOEUVRING • Stabilisers 101 • Steering gear 109 • Rudders 117 Deck machinery solutions 123 ELECTRICAL POWER AND AUTOMATION SYSTEMS • Electrical power systems 145 • Automation systems 163 Global service and support 171 02 We are determined to provide our customers with innovative and dependable marine systems that ensure optimal operation at sea. By utilising and integrating our technology, experience and competencies within design, deck machinery, propulsion, positioning, detection and automation we aim to give our customers the full picture - shaping the future of the maritime industry. Our industry expertise covers a fleet of more than 30,000 vessels. While we are the largest marine technology specialist organisation in the world, with the most extensive product and knowledge base, our focus continues to be on customers and the environment. Only by listening to you and predicting industry needs can we enable the transformation needed to put safety and sustainability first, while continuing to generate value for all stakeholders. The Full Picture consists of our product portfolios, world class support networks and more than 3500 expert staff located in 34 countries across the globe. We are shaping the maritime future with leading edge operational technology, solutions for big data and digital transformation, new electric and hybrid power systems and truly game-changing developments in remote operations and Maritime Autonomous Surface Ships (MASS).
    [Show full text]
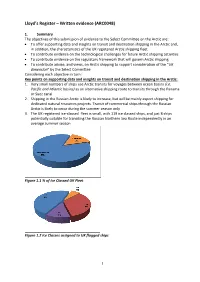
  • Lloyd's Register – Written Evidence (ARC0048)
    Lloyd’s Register – Written evidence (ARC0048) 1. Summary The objectives of this submission of evidence to the Select Committee on the Arctic are: To offer supporting data and insights on transit and destination shipping in the Arctic and, in addition, the characteristics of the UK registered Arctic shipping fleet. To contribute evidence on the technological challenges for future Arctic shipping activities To contribute evidence on the regulatory framework that will govern Arctic shipping To contribute advice, and views, on Arctic shipping to support consideration of the “UK dimension” by the Select Committee Considering each objective in turn: Key points on supporting data and insights on transit and destination shipping in the Arctic: 1. Very small numbers of ships use Arctic transits for voyages between ocean basins (i.e. Pacific and Atlantic basins) as an alternative shipping route to transits through the Panama or Suez canal 2. Shipping in the Russian Arctic is likely to increase, but will be mainly export shipping for dedicated natural resources projects. Transit of commercial ships through the Russian Arctic is likely to occur during the summer season only 3. The UK registered ice-classed fleet is small, with 119 ice classed ships, and just 8 ships potentially suitable for transiting the Russian Northern Sea Route independently in an average summer season Figure 1.1 % of Ice Classed UK Fleet Figure 1.2 Ice Classes assigned to UK flagged ships 1 Key points on the technological challenges for future Arctic shipping activities: 1. Technological challenges remain for efficient Arctic shipping with a significant build and operating cost premium associated with current generation of Arctic capable ships 2.
    [Show full text]
  • A Procedure for the Dynamic Positioning Estimation in Initial Ship-Design
    A Procedure for the Dynamic Positioning Estimation in Initial Ship-Design Syed Marzan Ul Hasan Master Thesis presented in partial fulfillment of the requirements for the double degree: “Advanced Master in Naval Architecture” conferred by University of Liege "Master of Sciences in Applied Mechanics, specialization in Hydrodynamics, Energetics and Propulsion” conferred by Ecole Centrale de Nantes developed at University of Rostock, Germany in the framework of the “EMSHIP” Erasmus Mundus Master Course in “Integrated Advanced Ship Design” EMJMD 159652 – Grant Agreement 2015-1687 Supervisor: Dr. Robert Bronsart , University of Rostock, Germany Reviewer: Dr. Lionel Gentaz, École Centrale de Nantes, France Rostock, February 2018 P 2 Syed Marzan Ul Hasan (This page is intentionally left blank) Master Thesis developed at University of Rostock, Germany Declaration of Authorship I, …………………………………………………………………………………………….Syed Marzan Ul Hasan declare that this thesis and the work presented in it are my own and has been generated by me as the result of my own original research. ………………………………………………………………………………………………………… A Procedure for the Dynamic Positioning Estimation in Initial Ship-Design ………………………………………………………………………………………………………… I confirm that: 1. This work was done wholly or mainly while in candidature for a research degree at this University; 2. Where any part of this thesis has previously been submitted for a degree or any other qualification at this University or any other institution, this has been clearly stated; 3. Where I have consulted the published work of others, this is always clearly attributed; 4. Where I have quoted from the work of others, the source is always given. With the exception of such quotations, this thesis is entirely my own work; 5.
    [Show full text]
  • Comparative Investigation on Influence of the Positioning Time of Azimuth Thrusters on the Accuracy of DP
    Author’s Name Name of the Paper Session DYNAMIC POSITIONING CONFERENCE October 9-10, 2012 Thrusters Comparative Investigation on Influence of the Positioning Time of Azimuth Thrusters on the Accuracy of DP D. Jürgens, M. Palm, A. Brandner Voith Turbo Marine, Heidenheim, Germany D. Jürgens, M. Palm, A.Brandner, Voith Voith Schneider Propeller 1. Introduction The Voith Schneider Propeller (VSP) allows extremely fast thrust variation [1]. Contrary to all other types of azimuth thrusters (thrust changes accordingly to polar coordinates), the thrust is varied on the basis of X/Y logic. Fig. 1 shows both thruster types; the Voith Radial Propeller (VRP) is an azimuth thruster developed by Voith Turbo Marine. As a result, ships with VSP can be kept stable in dynamic positioning (DP) mode, while the rolling motion of the vessel can also be reduced. DP capabilities and good sea handling are very important for the offshore industry. Fig. 1 Voith Schneider Propeller (VSP) and Voith Azimuth Thruster (VRP) In 2003, Voith Turbo Schneider Propulsion started to carry out intensive research programs aimed at making the VSP available to the offshore industry as an efficient propulsion system. These R & D activities focused primarily on the development of the Voith Roll Stabilization (VRS), model tests and CFD calculations on the interaction between the ship's hull and the propulsor ( [2], [3] and [4]). The first VSP-driven platform supply vessel is the Edda Fram (Fig. 2.) of Ostensjö Rederi AS. In the meantime, the vessel has demonstrated the successful application of VSPs in offshore service in over 35 000 operating hours.
    [Show full text]