DOCSLIB.ORG

Cutting Edge Preparation of Precision Cutting Tools by Applying Micro-Abrasive Jet Machining and Brushing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cutting Edge Preparation of Precision Cutting Tools by Applying Micro-Abrasive Jet Machining and Brushing Carlos Julio Cortés Rodríguez Cutting edge preparation of precision cutting tools by applying micro-abrasive jet machining and brushing kassel university press Die vorliegende Arbeit wurde vom Fachbereich Maschinenbau der Universität Kassel als Dissertation zur Erlangung des akademischen Grades eines Doktors der Ingenieurwissenschaften (Dr.-Ing.) angenommen. Erster Gutachter: Prof. Dr.-Ing. Franz Tikal Zweiter Gutachter: Prof. Dr.-Ing. Jens Hesselbach Tag der mündlichen Prüfung 17. April 2009 Bibliografische Information der Deutschen Nationalbibliothek Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie; detaillierte bibliografische Daten sind im Internet über http://dnb.d-nb.de abrufbar Zugl.: Kassel, Univ., Diss. 2009 ISBN print: 978-3-89958-712-8 ISBN online: 978-3-89958-713-5 URN: urn:nbn:de:0002-7135 © 2009, kassel university press GmbH, Kassel www.upress.uni-kassel.de Druck und Verarbeitung: Unidruckerei der Universität Kassel Printed in Germany iii Vorwort Die vorliegende Dissertation entstand wÄahrendmeiner Arbeit als Doktorand am Instituts fÄurProduktionstechnik und Logistik der UniversitÄatKassel im Fachgebiet Pro- duktionstechnik und Werkzeugmaschinen. Dem Fachgebietsleiter, Herrn Prof. Dr.-Ing. Franz Tikal, danke ich herzlich fÄur seine UnterstÄutzungund hilfreichen Anregungen, die diese Arbeit ermÄoglichten. Herrn Prof. Dr.-Ing. Jens Hesselbach, danke ich fÄurdie UbernahmeÄ des Korreferates. Den Herren Prof. Dr.-Ing. Eberhard Paucksch und Prof. Dr.-Ing. Wolfgang Klose danke ich fÄurdie Bereitschaft zur Teilnahme an der PrÄufungskommission. Mein Dank gilt darÄuber hinaus dem Kollegium des Fachgebiets, das durch die frucht- baren Discussionen und Anregungen zum Gelingen dieser Arbeit beigetragen hat. Der Universidad Nacional de Colombia danke ich fÄurdie UnterstÄutzungund der Stiftung COLFUTURO fÄurdie ¯nanzielle Hilfe. Der KAAD danke ich fÄurdie GewÄahrung eines Stipendiums Äuber 22 Monate und dem ALBAN Programm danke ich fÄurdie GewÄahrung eines Stipendiums Äuber 18 Monate. Ein besonderer Dank gilt meinen Eltern Luis und Alicia, die meine Ausbildung ermÄoglicht haben und meiner Frau Patricia und meinen Kindern Sebastian und Juliana fÄurdie liebevolle UnterstÄutzungund die mir ihre Geduld und Zeit geschenkt haben. Kassel, im April 2009 Carlos Julio Cort¶esRodr¶³guez iv Abstract For the systemic development of precision cutting tools, it is indispensable to observe four related aspects; the cutting tool material, the coating technology, the macro geometry of the tool and the cutting edge preparation. The present work is focused on the last aspect. In accordance with the speci¯ed requirements of the machining process to achieve the quality characteristics of the workpiece, it is necessary to keep in mind the speci¯cations of the cutting tool and particularly their cutting edge preparation. Therefore, to achieve a cutting edge preparation to satisfy the requirements, in terms of reproducibility, quality, cost and flexibility, the selection and planning of the preparation process has special im- portance. In this work, in ¯rst instance, a reproducible methodology of characterization of the cutting edge preparation was proposed, in terms of micro and meso geometry of the cutting tool, as well as the corresponding required measurement strategy by using a chromatic sensor. For the above-mentioned, concepts of di®erential geometry and fractal geometry were used, together with the existent international norms for surface measure- ment. Considering this characterization of the geometry of the cutting edge, three cutting edge preparation processes for cemented carbide tools were analyzed; micro-abrasive jet machining, brushing-polishing and brushing with abrasive ¯laments. By using design of experiments (DoE) and regression analysis, the influence of the process parameters on the quantity of removed material and on the characteristics of the surface of the cutting tool was observed. Aspects as radius of the cutting edge, notchedness (chipping) of the cutting edge, and microstructuring of the cutting tool surfaces were considered for each process. Additionally, machining experiments to observe the influence of the radius of the cutting edge and the preparation process on the cutting forces and the wear of the cutting tool were carried out. With the obtained information from DoE and regression analysis, as well as of the machining experiments, the considered preparation processes can be evaluated, compared, selected and planned. A planning strategy for cutting edge preparation processes considering the nominal removed area as process time function, and an equation to express the development of the notchedness as function of process time, was proposed. The presented aspects of process planning can be applied to other preparation processes. By using DoE, the variability of the obtained cutting edge radius is analyzed, and experimental models that express the removed area as function of the process parameters for the considered preparation processes, were developed. Considering the results of orthogonal cutting tests, the prepa- ration by means of rounding of the cutting edge has a positive e®ect, compared with sharp edges, in the decrease of the cutting forces and force ratio after that a critical point in the development of the test was reached. Additionally, the tools with rounded cutting edges showed a lower ¯nal flank wear than the sharp edges. Di®erences in flank wear for cutting edges with the same radii but obtained by di®erent preparation processes can be explained by di®erences in notchedness and microstructuring. Likewise, the existence of an optimal radius that causes the lower ¯nal flank wear, is observed. v Kurzfassung FÄureine systematische Entwicklung von PrÄazisionszerspanungswerkzeugen, ist es not- wendig vier zusammenhÄangendeAspekte zu beachten: den Schneidsto®, die Beschich- tungstechnologie, die Makrogeometrie und die SchneidkantenprÄaparation.Die vorliegende Arbeit behandelt den letzten dieser vier Aspekte. Bestimmte Anforderungen an die Zerspanungsverfahren sind notwendig, um die geforderten QualitÄatsmerkmalevon Bau- teilen zu garantieren. Es ist daher erforderlich die Spezi¯kationen der Zerspanungswerk- zeuge zu kennen, insbesondere die SchneidkantenprÄaparation.Hierbei spielt die Auswahl und Planung der SchneidkantenprÄaparationeine wichtige Rolle um den Anforderungen in Hinblick auf Reproduzierbarkeit, QualitÄat,Kosten und FlexibilitÄatzu genÄugen. In dieser Arbeit wird an erster Stelle eine Methode zur Charakterisierung der Schneidkan- tenprÄaparationin Hinblick auf Meso- und Mikrogeometrie vorgeschlagen, welche mit Hilfe entsprechender Messtechnik und basierend auf dem Einsatz eines chromatischen Sensors durchgefÄuhrtwird. FÄurdiese Methode wurden Konzepte der di®erentiellen und frak- talen Geometrie, sowie internationale Normen zur Oberfl¨achenmessung angewendet. Zur vorgeschlagenen Charakterisierung der Geometrie der Schneidkante, wurden drei Schneid- kantenprÄaparationsverfahren von Hartmetallwerkzeugen analysiert: Mikrostrahlen, BÄurs- ten-Polieren und BÄurstenmit abrasiven Filamenten. Mittels statistischer Versuchsplanung (DoE) und der Regressionsanalyse wurde der Einfluss der Prozessparameter auf das Ab- tragsmaterial und auf die Merkmale der Werkzeugoberfl¨achen bestimmt. Weitere Aspekte wie der Schneidkantenradius, Schartigkeit und die Mikrostrukturierung der Span- und Freifl¨ache, wurden fÄurjedes SchneidkantenprÄaparationsverfahren untersucht. ZusÄatzlich wurden Zerspanungsversuche durchgefÄuhrt,um den Einfluss des Schneidkantenradius und der PrÄaparationsverfahren auf die SchnittkrÄafteund den Freifl¨achenverschlei¼ zu be- stimmen. Mit den Ergebnissen der statistischen Versuchsplanung, der Regressionsanalyse sowie der Zerspanungsversuche kÄonnenverschiedene PrÄaparationsverfahren verglichen, ausgewertet, geplant und ausgewÄahltwerden. Eine Planungsstrategie zur Schneidkantenverrundung unter BerÄucksichtigung der Abtragsfl¨ache, der Abtragsrate und eine Gleichung zum Verhalten der Schartigkeit als Funktion der Bearbeitungszeit werden vorgeschlagen. Durch DoE werden die Streuung des erzielten Kantenradius bestimmt und experimentelle Modelle vorgeschlagen, um die Abtragsfl¨ache als einen Parameter bei der PrÄaparationsverfahren mit einzubinden. In Anbetracht der Ergebnisse der Versuche mit Orthogonalprozessen und im Vergleich mit scharfen Kanten hat die Verrundung der Schneidkante einen positiven E®ekt in Bezug auf die Verringerung der SchnittkrÄaftenach dem kritischen Punkt. ZusÄatzlich zeigten die Werkzeuge mit verrundeten Schneidkanten am ende der Versuche einen niedrigeren Freifl¨achenverschlei¼ als solche mit scharfen Kanten. Unterschiede des Freifl¨achenver- schlei¼es bei Kanten mit gleichen Radien aber verschiedenen PrÄaparationsverfahren kÄonnen durch Unterschiede in der Schartigkeit und der Mikrostrukturierung erklÄartwerden. Eben- so wird beobachtet, dass ein optimaler Radius den Freifl¨achenverschlei¼ reduzieren kann. vi Contents Vorwort iii Abstract iv Kurzfassung v Nomenclature xi 1 Introduction 1 2 Problem outline and objectives 3 2.1 Problem de¯nition . 3 2.2 Research objectives . 8 2.3 Methodology . 8 3 Fundamentals 9 3.1 Importance and purposes of the cutting edge preparation . 9 3.2 Cutting edge preparation geometries . 13 3.3 Factors influencing the cutting edge geometry . 15 3.4 Influence of the cutting edge preparation in machining . 16 3.4.1 Size e®ect and micromachining . 17 3.4.2 Chip formation . 22 3.4.3 Forces, strain and stresses
Load more

Recommended publications
  • Drill Press Operator: Instructor's Guide
    DOCUMENT RESUME 2D 109 N77 CE 004 335 AUTHOR Kagan, Alfre d; And Others TITLE -Drill Press Operator: Instructor's Guide. INSTITUTION New York State Education Dept., Albany. Bureau of Continuing Education Curriculum Development.; New York State Education Dept., Albany. Bureau of Secondary,Curriculum Development. PUB DATE 75 NOTE . 85p.; Part of SingleTool Skills Program, Machine Industries Occupations EDRS PPICE MIP-$0.76 HC-$4.43 PLUS POSTAGE DESCRIPTORS Adult Education; *Curriculum Guides; Machine Tool Operators; *Machine Tools; Metal Working Occupations; Post Secondary Education; Secondary Education; Shop Curriculum; *Trade and Industrial Education IDENTIFIERS *Drill Press Operators ABSTRACT The course is intended to kelp meet, in a relatively short time, the need for trained operators in metalworking. It can be used by students with little education or experience and is suitable far use in adult education programs and in manpower development and training progress. The course is designed' to be completed in approximately 30 weeks and can be adapted for use in secondary 'schools. On successful completion of the course the student will be qualified for an entry-level job as operator in a drill press; he will not qualify as a eachinist. The guide includes h general job content outline for the teacher to use in explaining what the operator's job includes. There are Il shop projects (comprising 19 jobs) accompanied by 32 pages of drawings for the projects. Three of the jobs introducb students to the use of metric measurement. For each job there is a job sheet providing details on performance objectives, equipment, operations, materials, references, procedure, techniques, and time required.
    [Show full text]
  • Surface Plates
    CALL US TODAY +1-262-422-1197 BUSCH PRECISION EQUIPMENTcan help you… Improve manufacturing efficiency and quality • Reduce costs and increase profits Worldwide consumer preference for L better products and the accompanying development of international quality standards demands meticulous QUALITY attention to accuracy in all phases of ASSURANCE & manufacturing. PRODUCT This catalog describes over 300 standard SATISFACTION types and sizes of basic precision Since 1907, BUSCH has been equipment designed to: serving industry’s basic precision equipment needs. L Facilitate layout of tooling As a diversified full-service L Speed production and assembly machine center, as well as a L Simplify and speed inspection manufacturer of precision equipment, we know and use the L Provide quality assurance products. Every effort is made to provide the highest quality products consistent with cost and material availability. Each In addition to the standard items item is carefully inspected and calibrated to insure conformance illustrated in this catalog, we also to specified tolerances and for compliance with all recognized design and manufacture custom standards. Inspection and calibration are performed by equipment to meet special applications. qualified technicians using appropriate state-of-the-art instrumentation. We also recondition worn or repair Certification of Accuracy is available for any item on request damaged equipment. This can be a and such certification is traceable to the National Institute of wise financial move in that regrinding Standards and Technology (NIST). Detailed information on our out-of-tolerance items can be calibration and inspection procedures and instrumentation can accomplished at considerable savings be found on page 19. over replacement cost.
    [Show full text]
  • E-1 Small Tool Instruments and Data Management Gauge Blocks Height
    Small Tool Instruments and E Data Management INDEX Gauge Blocks Features E-2 Gauge Blocks Accuracies E-4 Metric Rectangular Gauge Block Sets E-6 Inch Rectangular Gauge Block Sets E-11 Micrometer Inspection Gauge Block Sets E-12 Caliper Inspection Gauge Block Sets E-13 Individual Metric Rectangular Gauge Blocks E-14 Individual Inch Rectangular Gauge Blocks E-16 Height Master Rectangular Gauge Blocks with CTE E-17 ZERO CERA BLOCKS E-17 Rectangular Gauge Block Accessories E-18 Metric Square Gauge Block Sets E-20 Inch Square Gauge Block Sets E-21 Individual Metric Square Gauge Blocks E-22 Reference Gages Individual Inch Square Gauge Blocks E-23 Square Gauge Block Accessories E-24 Ceraston E-26 Maintenance Kit for Gauge Blocks E-26 Step Master E-27 Custom-made Blocks & Gages E-27 Gauge Block Interferometer GBI E-28 Granite Surface Gauge Block Comparator GBCD-100A E-28 Plates & Bench Gauge Block Comparator GBCD-250 E-29 Gauge Block Comparator GBCS-250 E-29 Comparator Height Master Height Master E-30 Digital Height Master E-30 CERA Height Master E-31 Auxiliary Block Kit E-31 Riser Blocks E-31 Universal Height Master E-32 Check Master E-33 Reference Gages Standard Scales E-34 Working Standard Scales E-34 CERA Straight Master E-35 Snap Gage Checker E-36 High Precision Square E-36 CERA/Steel Combination Square Master E-37 Gauge Block Sets Precision Square E-38 Precision Dial Square E-38 Combination Square Set E-39 E Steel Rules E-40 Thickness Gages E-41 Radius Gages E-42 Thread Pitch Gages E-42 E Digital Universal Protractor E-43 Universal Bevel
    [Show full text]
  • Performance Standards Vertical Milling Level I
    Performance Standards Vertical Milling Level I Material Mild steel or low carbon steel 1.5" x 2" x 2.6" Duty Setup and operate vertical milling machines. Perform routine milling, and location of hole centers within +/-.005". Performance Standard Given raw material, print, hand, precision, and cutting tools, as well as access to an appropriate vertical milling machine and its accessories, produce a part matching the blueprint specifications using appropriate trade techniques and speeds and feeds. The part specified should require squaring up from the raw state, have at least one milled slot, require the location of at least two drilled and reamed holes within positional tolerance of .014” and have three steps controlled by tolerances of +/-.005". Other Evaluation Criteria 1. Finishes are at least 125 Ra microinches. 2. No sharp edges. Accuracy Level: +/- .015 on all fractions, +/-.005 on all decimals unless otherwise specified on the blueprint. Finishes Surfaces to be square within .005 over 4". Finished surfaces are to be 125 Ra microinches unless otherwise specified. Assessment Equipment and Material Workstation: A common workbench, a vertical mill. Table capacity of approximately 12"X36". Material: A part matching the material requirements of the vertical milling print, material: Mild steel. Tooling: A 6" milling vise or greater, screws, studs, nuts, washers, and clamps sufficient to secure the vise, or the part to the table. Assorted parallels, ball peen, and soft-faced hammers, assorted cutters and cutter adapters fitted to the machine spindle, files, magnetic base for indicators, soft jaws for the vise, drill chuck, drills, reamers, combination drill and countersink or spotting drill, countersink, and edge finder.
    [Show full text]
  • Evaluation Instructions Machining Level II Grinding: Flats and Angles
    Evaluation Instructions Machining Level II Grinding: Flats and Angles General Instructions 1. Make sure that the candidate has his/her own copy of the part print, job instructions and understands the criteria for performance evaluation. Times indicated are guidelines and will not be part of the assessment. 2. Provide access to the tools, equipment and materials as suggested on the next page. 3. Identify each candidate’s work upon completion and permanently mark all parts. 4. Complete the evaluation of the candidate’s project as soon as possible after completion. Be sure to complete the SPONSOR portion of the Performance Affidavit for successful projects. Monitoring the Performance 1. Make sure that the steel block used to complete the project agrees with the specifications on the part print. 2. Always check to see that the candidate is using the workholding devices and tooling in a safe and secure manner. 3. Check that all personal protection and safety precautions are being employed. Stop any candidate from creating an unsafe condition. A candidate should not be allowed to start, continue, or return to the project until an unsafe condition is resolved. If the unsafe condition is of the candidate’s making, the evaluator or sponsor should require that the candidate completely restart the project after the safety issue has been resolved and appropriate instruction has been given. Completion of the Performance Evaluation 1. Check to see that the candidate has provided proper cleanup of tools, equipment and work area. 2. Check to see that tools are returned to their proper storage locations. 3.
    [Show full text]
  • Introduction Machine Types
    Introduction In this part of the Molex eGUIDE we will discover and learn the operations and procedures that go behind surface grinding. As you learn you would appreciate the process of producing and finishing flat surfaces and you would find yourself better adapted to the processes and demands on work at the Molex tool room. We will begin with a definition on grinding and then focus on surface grinding to understand machine types, machine know-how and the surface grinding process that is demonstrated on the job - to help you identify with best practices adopted at Molex. This course is intended to serve as a guide to on the job demands and hence it is treated with a practical approach covering all facets of surface grinding as a process with the niceties of this grinding technology. How would one define grinding? Grinding is a process of fine metal cutting, achieved by the action of many small individual abrasive grains. These abrasive grains are formed into a grinding wheel that is rotated against the work piece at high speeds. Grinding machines and grinding processes are essential to most manufacturing industries, and at Molex we have proven our expertise with very high precision work covering Surface Grinding, Profile grinding, CNC Surface grinding, CNC Jig Grinding and CNC Optical Profile Grinding. Having understood the process of grinding, let's understand - What surface grinding is about? Surface Grinding is the process of producing and finishing flat surfaces by means of a grinding machine employing a revolving abrasive wheel. Machine Types Surface grinding is performed on two different types of surface grinding machines that are differentiated by the position of the grinding wheel spindle in relation to the table that holds the work.
    [Show full text]
  • NIMS Machining Level I Preparation Guide Grinding
    NIMS Machining Level I Preparation Guide Grinding Table of Contents Overview pages 2 - 6 · Introduction page 2 · Who Wrote the Questions page 2 · How to Prepare for the Credentialing Exam page 3 · Areas of Knowledge Measured by the Credentialing Exam pages 3 - 5 · Before the Credentialing Exam page 5 · At the Testing Site page 6 Machining Exam – Grinding pages 7 - 28 · Credentialing Exam Content, Sample Question Overview page 7 · Credentialing Exam Specifications page 8 · Task List pages 9 - 25 · Sample Exam pages 9 - 25 · Answer Key pages 26 - 28 © 2003 National Institute for Metalworking Skills, Inc. Page 1 of 28 Overview Introduction This preparation guide or test advisor is intended to help machinists study and prepare for the National Institute for Metalworking Skills (NIMS) written credentialing exam. The sample exam will prepare machinists to take the actual credentialing exam. None of the questions are duplicates from the actual credentialing exam. However, this preparation guide is a useful tool for reviewing technical knowledge and identifying areas of strength and deficiency for adequate credentialing exam preparation. Achieving a NIMS credential is a means through which machinists can prove their abilities to themselves, to their instructors or employers and to the customer. By passing the NIMS credentialing exam, you will earn a valuable and portable credential. Because the credentialing exam is challenging, you will have the satisfaction of proving to yourself and others that you have reached a level of competency that is accepted nationally. Who Wrote the Questions A panel of technical experts, from all areas of the metalworking industry, wrote the questions used on the actual credentialing exam.
    [Show full text]
  • Dedicated to Accuracy and Precision
    Opus Precision Flat Lapping Service The Opus Precision Flat Lapping Service can DEDICATED TO ACCURACY AND PRECISION be applied to a wide range of materials and our expertise and skills in flat lapping are applied to a diverse range of components for the Oil & Gas, Aerospace, Printing, Automotive, Medical and Electronic industries. Flat Lapping is ideal for close tolerance work. Opus can work to a flatness and parallelism tolerance of 0.05 μm and thickness to ± 0.05 μm (size, shape and material dependant). Whilst most materials can be lapped, Opus has particular experience with all types of steel (including stainless), tungsten carbide, various ceramics (including PZT), copper, aluminium and titanium. A range of finishes can also be produced ranging from highly reflective, mirror like finishes to satin and matt finishes depending upon the material. Flat Lapping projects can be verified in our temperature controlled laboratory. Our flat lapping service offers highly specialised hand lapping techniques to suit one-off component parts and for large quantity components we offer machine lapping on single sided or double sided lapping machines. Our extensive range of plant and equipment includes surface grinders, single and double sided lapping machines, Fizeau laser flatness interferometers, Talysurf 10, fibre laser marking machine and a temperature controlled fine lapping department. Opus Special Manufacturing FREE UKAS Opus’s Special Manufacturing is based upon the Calibration Certificate combination of traditional tool making skills with upon request experience gained in reference gauge manufacturing and special lapping skills. Opus can manufacture and verify gauges, precision fixtures and components to very close tolerances that can seldom be matched by other companies.
    [Show full text]
  • Drilling Machines General Information
    TC 9-524 Chapter 4 DRILLING MACHINES GENERAL INFORMATION PURPOSE USES This chapter contains basic information pertaining to drilling A drilling machine, called a drill press, is used to cut holes machines. A drilling machine comes in many shapes and into or through metal, wood, or other materials (Figure 4-1). sizes, from small hand-held power drills to bench mounted Drilling machines use a drilling tool that has cutting edges at and finally floor-mounted models. They can perform its point. This cutting tool is held in the drill press by a chuck operations other than drilling, such as countersinking, or Morse taper and is rotated and fed into the work at variable counterboring, reaming, and tapping large or small holes. speeds. Drilling machines may be used to perform other Because the drilling machines can perform all of these operations. They can perform countersinking, boring, operations, this chapter will also cover the types of drill bits, counterboring, spot facing, reaming, and tapping (Figure 4-2). took, and shop formulas for setting up each operation. Drill press operators must know how to set up the work, set speed and feed, and provide for coolant to get an acceptable Safety plays a critical part in any operation involving finished product. The size or capacity of the drilling machine power equipment. This chapter will cover procedures for is usually determined by the largest piece of stock that can be servicing, maintaining, and setting up the work, proper center-drilled (Figure 4-3). For instance, a 15-inch drilling methods of selecting tools, and work holding devices to get machine can center-drill a 30-inch-diameter piece of stock.
    [Show full text]
  • NIMS Machining Level I Preparation Guide Milling
    NIMS Machining Level I Preparation Guide Milling Table of Contents Overview page 2 - 5 · Introduction page 2 · Who Wrote the Questions page 2 · How to Prepare for the Credentialing Exam page 3 · Areas of Knowledge Measured by the Exam pages 3, 4 · Before the Exam page 5 · At the Testing Site page 5 Machining Exam – Milling pages 6 - 31 · Exam Content and Sample Question Overview page 6 · Task Specifications page 7 · Task List pages 7 - 25 · Sample Exam pages 8 - 26 · Answer Key pages 26 - 31 © 2003 National Institute for Metalworking Skills, Inc. Page 1 of 31 Overview Introduction This preparation guide or test advisor is intended to help machinists study and prepare for the National Institute for Metalworking Skills (NIMS) written credentialing exam. The sample test will help prepare machinists to take the actual credentialing exam. None of the questions are duplicates from the actual exam. However, this preparation guide is a useful for reviewing technical knowledge and identifying areas of strength and deficiency needed so that the student has what is needed to do well on the exam. Achieving a NIMS credential is a means through which machinists can prove their abilities to themselves, to their instructors or employers and to the customer. By passing the NIMS credentialing exam, you will earn a valuable and portable credential. Because the test is challenging, you will have the satisfaction of proving to yourself and others that you have reached a level of competency that is accept nationally. Who Wrote the Questions A panel of technical experts, from all areas of the metalworking industry, wrote the questions used on the actual credentialing exam.
    [Show full text]
  • Kurt General Catalog.Pdf
    KURT® KURT PH 763.574.8309 email [email protected] www.kurtworkholding.com Introduction .................................2 HD CarvLock Towers ........... 18-21 VersatileLock Vises (3400)... 40-41 InnerLock Jaw Plates ................65 Kurt Torque Handle TH6 ............69 Application Chart .........................3 Rotary Table Workholding .........22 AngLock PT-Series Vises ..... 42-43 Machinable Jaw Plate ...............65 Replacement Vise Handles ........69 NEW SideWinder ...................... 4-5 HD/HDL Vise How To Order ........23 Custom Workholding ........... 44-45 Standard Jaw Plates ..................65 Handle Hanger ...........................69 NEW PinLock Mounting System HD/HDL Jaws Kits and Back to Back Vises .............. 46-47 Groove Lock ...............................66 Vise Screw Hex Extensions........69 and Receiver Bushings ............ 6-7 Fixture Plates ....................... 24-27 MoveLock Modular System . 48-49 Magnetic Jaw Plate and Spanner Wrench ........................69 NEW MaxLock 350 DoubleLock Vises ................ 28-29 MiniLock .............................. 50-51 Parallel Set ................................66 Swivel Base ...............................70 Multi-Axis Vise .............................8 ClusterLock Cluster Tower.........30 Self-Centering Vise .............. 52-53 6" Magnetic Jaw Plates.............66 Sine Keys (Non-Expandable NEW MaxLock SCMX425 & ClusterLock ................................31 NEW Sine Plates ........................67 SCMX250 Multi-Axis Vise ............9 Extra
    [Show full text]
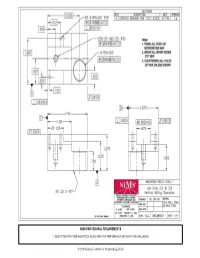
  • NIMS Step Block General Procedure
    NIMS PROCEDURAL REQUIREMENTS 1. SUBMIT THIS PRINT AND WORKPIECE ALONG WITH THE PERFORMANCE AFFIDAVIT FOR EVALUATION © 2005 National Institute for Metalworking Skills NIMS Step Block General Procedure 1) Cut a piece of 1.5” X 2” mild steel stock to a length of 2.625” on the bandsaw. Tools used: Combination square 2) Tram the milling machine head within .0005” per 6”. Tools used: Tramming plate, .0005”-reading test indicator, Indicol holder 3) Square the stock and rough the overall dimensions to .030” oversize (ie 1.405” X 1.905” X 2.530”). Tools used: SECO Octomill, HSS end mill, dial caliper, parallels, brass pin 4) Rough the steps and slot to .030” oversize on all linear dimensions. a. bottom step: 1.530” from Datum C and .780” from Datum A b. top step: 1.030” from Datum C and 1.155” from Datum A c. slot: .75” wide and 1.030” from Datum A Tools used: Weldon-style end mill holder, HSS roughing end mill, dial caliper, drill chuck, edgefinder (to find part center to cut slot), parallels 5) Pre-drill the large hole. Tools used: Drill chuck, edgefinder, #4 center drill, 11/16” drill, parallels (max 1/8” thick) 6) Finish all outside surfaces in the proper sequence to establish final sizes and GD&T controls. a. Datum feature A b. Datum feature C c. Datum feature D d. Side opposite datum feature C e. Side opposite datum feature D Tools used: R8 collet, flycutter with brazed carbide tool, .0005”-reading test indicator, Indicol holder, outside micrometers, parallels 7) Finish steps and top surface (side opposite datum feature A) to establish final sizes.
    [Show full text]