DOCSLIB.ORG

Ion Channels and Electrical Activity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ion Channels and Electrical Activity 10/10/2012 ION CHANNELS AND ELECTRICAL ACTIVITY Colin Nichols Department of Cell Biology and Physiology Center for Investigation of Membrane Excitability Diseases Box 8228 9611 BJC-IH 362-6630 [email protected] http://www.nicholslab.wustl.edu/nichols.htm http:www.cimed.wustl.edu Many of the figures in the following notes come from Hille, B. ‘Ion Channels of Excitable Membranes’, Sinauer Associates, Sunderland, Mass. This is highly recommended to anyone interested in following up the lectures, and is essential reading to anyone interested in pursuing research on ion channel structure and function. Further background material can be found in: Lodish et al., Molecular Cell Biology, 4th ed, chapter 15 (p. 633-665) and chapter 21 (p. 925-965) and Alberts et al., Molecular Biology of the Cell, 4th ed, chapter 11 (p. 615-650) and p. 779-780. Overview These notes provide additional background to the lectures. The first section is an extended discussion of ion channel structure and function, followed by the classical description of the action potential and the role of ion channels in it. 1 1. Electrical principles A. Electrical properties of membranes In order to understand the electrical properties of cells we need to review the following principles of electricity: 1) Current, 2) Voltage, 3) Resistance/Conductance, 4) Capacitance All matter is made up of charged particles - protons and electrons. Charge is symbolized Q and is measured in Coulombs. The elementary charge of one electron or proton is e = 1.602 X 10-19 Coulombs. Faraday's constant (F) is the number of Coulombs per mole of particles that bear a single + or - charge. F = 9.648 * 104 Coulombs / mole. Charged particles move. They attract and repel each other. 1) Current (I) measures the rate of movement of the charge: I = Q / t = Coulombs / sec = Amps (A) 2) Voltage (V) is a measure of the difference in potential energy experienced by a charged particle in two locations. It is the work required to move a charge from point A to point B: V = Joules / Coulomb = Volts (V) 3) Resistance/Conductance Ohm's Law states that Current through a piece of homogeneous material is proportional to the Voltage applied across the material. Conductance (G) is the proportionality factor between current and voltage. The unit for Conductance is the Siemen (S). Resistance (R) is the inverse of conductance. It is measured in Ohms (). G = 1 / R Conductance = 1 / Resistance Ohm's Law I = G V or 1 Amp = 1 Siemen * 1 Volt V = I R 1 Volt = 1 Amp * 1 Ohm Resistance and Conductance depend on the size and shape of the object that you are passing current through. Resistivity (units = cm) is an intrinsic property of a homogeneous material that reflects its ability to carry current. For a right circular cylinder: R = Resistivity (Length / Area of a Cross Section) Sample Calculation - Consider a cylindrical pore 10 Angstroms in diameter and 50 Angstroms long that spans a lipid bilayer. The pore contains saline with resistivity of 60 cm (the resistivity of the bilayer is about 1015 cm). What is the resistance of this pore to axial current? 2 (Remember: 1 Angstrom = 10-10 m = 10-8 cm = 0.1 nm) 60 cm 50 10-8 cm 9 R = 3.1416 (5 10-8 cm) 2 = 4 X 10 or 4 Giga For Resistors "In Series" For Resistors "In Parallel" RTot = R1 + R2 + R3 . + Rn 1 / RTot = (1 / R1) + (1 / R2) + (1 / R3) . + (1 / Rn) Separation of + and - charges produces a potential difference or Voltage. 4) Capacitance (C) is a measure of how much charge must be separated to give a particular voltage. C (Farads) = Q (Coulombs) / V (Volts) or Q = C V And I = Q / t = C V / 2 Since Q = C * V, for a 1 cm region of membrane to be charged to 60 mV would require: -8 1.0 µF * 0.060 V = 6 X 10 Coulombs or 375 X 109 ions or 0.622 pico moles. t The capacitance of a physical object depends on its geometry. For a parallel plate capacitor: C = o Area / distance between the plates where is the dielectric constant of the material between the plates and o is the permittivity of free space (8.85 X 10-12 Coulomb / Volt Meter). Capacitance increases with increasing surface area and decreases as the separation between the plates becomes greater. The cell membrane with saline on both sides is very similar to a parallel plate capacitor. The lipid bilayer of most cells has a specific capacitance of 1.0 µFarad / cm2. By separating charge on either side of the membrane you develop a potential difference across the membrane. Only a small number of charges must be separated to result in a significant voltage. A simple model cell: Consider a spherical cell with several conducting pores. The cell contains saline and is bathed in saline. The equivalent circuit is a capacitor and a resistor in parallel. If we inject a square pulse of current into the cell with a microelectrode, some of it will charge the membrane capacitance and some will pass through the resistance of the conducting pores. ITot = IR + IC where IR = Vm / R and IC = C Vm / t Vm / t = (ITot / C) - (Vm / (RC)) The solution of this differential equation is: Vm = ITot R (1 - exp(-t / )) where = R C is the membrane time constant, the membrane potential of the cell will change along an exponential time course that is governed by . At equilibrium, when t >> Vm = ITot R , where R = 1 / Gpores is called the Input Resistance of the cell. 3 Surface Area of a Sphere of Radius r is A = 2 Sample Calculation - Consider a spherical cell, 4 r 100 µm in diameter, that has 200 open channels, each with a conductance of 10 pS. R = 0.5 GOhms -4 2 -4 Area = 4 3.1416 (50 X 10 cm) C = 3.1 X 10 µF -4 2 t = 155 msec = 3.1 X 10 cm Vm and C = 3.1 X 10-4 µF (mV) GTot = 200 10 pS 8 so Rin = 1 / GTot = 5 X 10 and = Rin C = 155 msec I = 5 pA time (msec) Modeling changes in Vm in a cell membrane Physical diagrams and electrical equivalence circuits showing how current injection from an electrode (left) or current entry through channels selective for sodium (right) can change the membrane potential. 4 The figures below, taken from Jack, Noble and Tsien Electric Current Flow in Excitable Cells (1983), illustrate the change in potential across a resistor and capacitor in parallel. The dashed and dotted lines in the figure on the right show the fraction of total current that is flowing through the resistor (IR) and charging the capacitor (IC), respectively. We said above that IR = Vm / Rm so the time course of IR will be identical to the change in membrane potential. IC = ITot - IR shows that initially all of the current goes to charging the capacitor. As charge builds up on the capacitor, the rate of addition of more charges decreases exponentially. Notice that at the end of the current pulse IC has the opposite sign. B. The Resting Potential An undisturbed cell at rest contains a slight excess of anions that produces a steady membrane potential, called the resting potential. The resting potential is usually in the range from -30 mV to -90 mV or so. Why do cells have ion channels and a resting potential? Cells live in an environment of dilute salt water. They contain within their cytoplasm a variety of impermeant solutes, including proteins and nucleic acids, but also smaller metabolites like amino acids, Kreb's cycle intermediates and so on. The sum total charge of these impermeant solutes is negative. Ion channels allow the cell to cope with the osmotic difficulties that result from confining these large charged ions inside the plasma membrane. The resting potential is an unavoidable consequence of the cell's strategy for handling changes in osmolarity. A cell needs to accommodate two physical facts - 1) The osmolarity of the cell's contents and the solution it is bathed in must be the same, otherwise water will flow into or out of the cell causing it to swell or contract. Cells will tolerate a bit of swelling, but not much. Since the environment may change at any moment, the cell needs to be able to adjust its internal osmolarity quickly. 2) There must be bulk neutrality of the two solutions - separation of tiny amounts of charge produce a substantial voltage across the membrane. An imbalance in the millimolar range is not physically sustainable. Let's examine several possible strategies the cell could use: 1) The cell could simply make its membrane impermeable to everything - this will not work because then slight changes in the external or internal osmolarity would exert great pressure on the membrane 5 2) The cell could be equally permeable to all ions - that won't work either because it would lead to osmotic imbalance. Ions will enter, causing the cell to expand and eventually burst. If impermeable and freely permeable will not work then the membrane has to be selectively permeable to a subset of ions. In order to allow for rapid adjustment of osmolarity, while preserving bulk neutrality, the membrane should be permeable to a cation and an anion. Most cell membranes are selectively permeable to potassium and chloride, but nearly impermeable to sodium ions, at rest. Consider the distribution of ions that might be typical for a frog neuron: (Concentration in mM) Out In Na+ 117 30 K+ 3 90 Cl- 120 4 Anions- 0 116 In addition to osmotic balance and bulk neutrality there is an additional thermodynamic restriction: All permeable ions will move toward electrochemical equilibrium.
Load more

Recommended publications
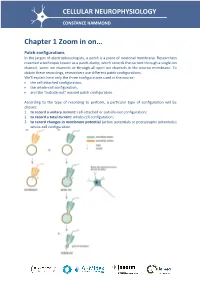
  • Chapter 1 Zoom in On… Patch Configurations in the Jargon of Electrophysiologists, a Patch Is a Piece of Neuronal Membrane
    CELLULAR NEUROPHYSIOLOGY CONSTANCE HAMMOND Chapter 1 Zoom in on… Patch configurations In the jargon of electrophysiologists, a patch is a piece of neuronal membrane. Researchers invented a technique known as a patch-clamp, which records the current through a single ion channel, some ion channels or through all open ion channels in the neuron membrane. To obtain these recordings, researchers use different patch configurations. We'll explain here only the three configurations used in the course: the cell-attached configuration, the whole-cell configuration, and the "outside-out" excised patch configuration. According to the type of recording to perform, a particular type of configuration will be chosen: 1. to record a unitary current: cell-attached or outside-out configuration; 2. to record a total current: whole-cell configuration; 3. to record changes in membrane potential (action potentials or postsynaptic potentials): whole-cell configuration. The cell-attached configuration (attached to the pipette - Figure a) First, the pipette is filled with an extracellular fluid. Positive pressure is applied in the electrode by means of a syringe connected to the electrode, so that the intrapipette fluid tends to leave the pipette. The electrode is then brought near to the soma of a neuron. When the electrode touches the membrane, the positive pressure is withdrawn to draw the membrane toward the mouth of the pipette. We wait without moving the pipette; a seal is made between the walls of the pipette and the soma membrane. This seal strength can be measured by applying a low level of amplitude current in the pipette. Since V = RI, one can measure the resistance of the seal.
    [Show full text]
  • Nernst Potentials and Membrane Potential Changes
    UNDERSTANDING MEMBRANE POTENTIAL CHANGES IN TERMS OF NERNST POTENTIALS: For seeing how a change in conductance to ions affects the membrane potential, follow these steps: 1. Make a graph with membrane potential on the vertical axis (-100 to +55) and time on the horizontal axis. 2. Draw dashed lines indicating the standard Nernst potential (equilibrium potential) for each ion: Na+ = +55 mV, K+ = -90mV, Cl- = -65 mV. 3. Draw lines below the horizontal axis showing the increased conductance to individual ions. 4. Start plotting the membrane potential on the left. Most graphs will start at resting potential (-70 mV) 5. When current injection (Stim) is present, move the membrane potential upward to Firing threshold. 6. For the time during which membrane conductance to a particular ion increases, move the membrane potential toward the Nernst potential for that ion. 7. During the time when conductance to a particular ion decreases, move the membrane potential away from the Nernst potential of that ion, toward a position which averages the conductances of the other ions. 8. When conductances return to their original value, membrane potential will go to its starting value. +55mV ACTION POTENTIAL SYNAPTIC POTENTIALS 0mV Membrane potential Firing threshold Firing threshold -65mV -90mV Time Time Na+ K+ Conductances Stim CHANGES IN MEMBRANE POTENTIAL ALLOW NEURONS TO COMMUNICATE The membrane potential of a neuron can be measured with an intracellular electrode. This 1 provides a measurement of the voltage difference between the inside of the cell and the outside. When there is no external input, the membrane potential will usually remain at a value called the resting potential.
    [Show full text]
  • Effect of Hyperkalemia on Membrane Potential: Depolarization
    ❖ CASE 3 A 6-year-old boy is brought to the family physician after his parents noticed that he had difficulty moving his arms and legs after a soccer game. About 10 minutes after leaving the field, the boy became so weak that he could not stand for about 30 minutes. Questioning revealed that he had complained of weakness after eating bananas, had frequent muscle spasms, and occasionally had myotonia, which was expressed as difficulty in releasing his grip or diffi- culty opening his eyes after squinting into the sun. After a thorough physical examination, the boy was diagnosed with hyperkalemic periodic paralysis. The family was advised to feed the boy carbohydrate-rich, low-potassium foods, give him glucose-containing drinks during attacks, and have him avoid strenuous exercise and fasting. ◆ What is the effect of hyperkalemia on cell membrane potential? ◆ What is responsible for the repolarizing phase of an action potential? ◆ What is the effect of prolonged depolarization on the skeletal muscle Na+ channel? 32 CASE FILES: PHYSIOLOGY ANSWERS TO CASE 3: ACTION POTENTIAL Summary: A 6-year-old boy who experiences profound weakness after exer- cise is diagnosed with hyperkalemic periodic paralysis. ◆ Effect of hyperkalemia on membrane potential: Depolarization. ◆ Repolarization mechanisms: Activation of voltage-gated K+ conductance and inactivation of Na+ conductance. ◆ Effect of prolonged depolarization: Inactivation of Na+ channels. CLINICAL CORRELATION Hyperkalemic periodic paralysis (HyperPP) is a dominant inherited trait caused by a mutation in the α subunit of the skeletal muscle Na+ channel. It occurs in approximately 1 in 100,000 people and is more common and more severe in males.
    [Show full text]
  • Electrical Activity of the Heart: Action Potential, Automaticity, and Conduction 1 & 2 Clive M
    Electrical Activity of the Heart: Action Potential, Automaticity, and Conduction 1 & 2 Clive M. Baumgarten, Ph.D. OBJECTIVES: 1. Describe the basic characteristics of cardiac electrical activity and the spread of the action potential through the heart 2. Compare the characteristics of action potentials in different parts of the heart 3. Describe how serum K modulates resting potential 4. Describe the ionic basis for the cardiac action potential and changes in ion currents during each phase of the action potential 5. Identify differences in electrical activity across the tissues of the heart 6. Describe the basis for normal automaticity 7. Describe the basis for excitability 8. Describe the basis for conduction of the cardiac action potential 9. Describe how the responsiveness relationship and the Na+ channel cycle modulate cardiac electrical activity I. BASIC ELECTROPHYSIOLOGIC CHARACTERISTICS OF CARDIAC MUSCLE A. Electrical activity is myogenic, i.e., it originates in the heart. The heart is an electrical syncitium (i.e., behaves as if one cell). The action potential spreads from cell-to-cell initiating contraction. Cardiac electrical activity is modulated by the autonomic nervous system. B. Cardiac cells are electrically coupled by low resistance conducting pathways gap junctions located at the intercalated disc, at the ends of cells, and at nexus, points of side-to-side contact. The low resistance pathways (wide channels) are formed by connexins. Connexins permit the flow of current and the spread of the action potential from cell-to-cell. C. Action potentials are much longer in duration in cardiac muscle (up to 400 msec) than in nerve or skeletal muscle (~5 msec).
    [Show full text]
  • The Action Potential
    See discussions, stats, and author profiles for this publication at: http://www.researchgate.net/publication/6316219 The action potential ARTICLE in PRACTICAL NEUROLOGY · JULY 2007 Source: PubMed CITATIONS READS 16 64 2 AUTHORS, INCLUDING: Mark W Barnett The University of Edinburgh 21 PUBLICATIONS 661 CITATIONS SEE PROFILE Available from: Mark W Barnett Retrieved on: 24 October 2015 192 Practical Neurology HOW TO UNDERSTAND IT Pract Neurol 2007; 7: 192–197 The action potential Mark W Barnett, Philip M Larkman t is over 60 years since Hodgkin and called ion channels that form the permeation Huxley1 made the first direct recording of pathways across the neuronal membrane. the electrical changes across the neuro- Although the first electrophysiological nal membrane that mediate the action recordings from individual ion channels were I 2 potential. Using an electrode placed inside a not made until the mid 1970s, Hodgkin and squid giant axon they were able to measure a Huxley predicted many of the properties now transmembrane potential of around 260 mV known to be key components of their inside relative to outside, under resting function: ion selectivity, the electrical basis conditions (this is called the resting mem- of voltage-sensitivity and, importantly, a brane potential). The action potential is a mechanism for quickly closing down the transient (,1 millisecond) reversal in the permeability pathways to ensure that the polarity of this transmembrane potential action potential only moves along the axon in which then moves from its point
    [Show full text]
  • Membrane Potentials As Signals
    Membrane Potentials as Signals The membrane potential allows a cell to function as a battery, providing electrical power to activities within the cell and between cells. KEY POINTS A membrane potential is the difference in electrical potential between the interior and the exterior of a biological cell. In electrically excitable cells, changes in membrane potential are used for transmitting signals within the cell. The opening and closing of ion channels can induce changes from the resting potential. Depolarization is when the interior voltage becomes more positive and hyperpolarization when it becomes more negative. TERMS Graded potentials Graded potentials vary in size and arise from the summation of the individual actions of ligand- gated ion channel proteins, and decrease over time and space. Depolarization Depolarization is a change in a cell's membrane potential, making it more positive, or less negative, and may result in generation of an action potential. Action potential A short term change in the electrical potential that travels along a cell such as a nerve or muscle fiber. EXAMPLE In neurons, a sufficiently large depolarization can evoke an action potential in which the membrane potential changes rapidly. Give us feedback on this content: Membrane potential (also transmembrane potential or membrane voltage) is the difference in electrical potential between the interior and the exterior of a biological cell. All animal cells are surrounded by a plasma membrane composed of a lipid bilayer with a variety of types of proteins embedded in it. The membrane serves as both an insulator and a diffusion barrier to the movement of ions.
    [Show full text]
  • 1 Probing the Membrane Potential of Living Cells by Dielectric
    Probing the membrane potential of living cells by dielectric spectroscopy Corina Bot and Camelia Prodan Dept. of Physics, New Jersey Inst. of Techn, Newark, NJ Abstract. In this paper we demonstrate a quantitative way to measure the membrane potential of live cells by dielectric spectroscopy. We also show that the values of the membrane potential obtained using our technique are in good agreement with those obtained using traditional methods-voltage sensitive dyes. The membrane potential is determined by fitting the experimental dielectric dispersion curves with the dispersion curves obtain from a theoretical model. Variations in the membrane potential were induced by modifying the concentration of potassium chloride in the solution of the cell suspension in the presence of valinomycin. For exemplification of the method, E. coli were chosen for our experiments. Introduction The resting membrane potential is one of the most important living cell parameters. By monitoring a cell’s membrane potential, one can get important information about its state. Changes in the membrane potential have been linked to different diseases, including Parkinson’s, epilepsy and Bartter’s syndrome [1]. A decrease in the plasma membrane potential has been seen in tumor cells with increased expression of multi-drug resistance (MDR) protein, also known as P-glycoprotein [2]. It was also shown that the membrane potential plays a critical role in the antibiotic uptake by cells and in bactericidal action [3]. Thus measuring or monitoring the membrane potential is of great importance. The existing “gold” or standard methods to measure or monitor the membrane potential are patch clamping and voltage sensitive dyes.
    [Show full text]
  • Resting Potential and Chloride Channels
    Neurobiology – resting potential and chloride channels Rudolf Cardinal, 4 Feb 99 • Ionic concentrations are determined and maintained by the activity of ionic pumps, including the Na+–K+ ATPase (pumping 3 + + + – + – + + Na out and 2 K in), the K /Cl cotransporter (using the K gradient to extrude Cl ), the active Ca pump (extruding Ca and us- ing ATP) and the Na+/Ca2+ exchanger (using the Na+ gradient to extrude Ca+, 3 Na+ in to 1 Ca2+ out). Action potentials involve the transfer of too few ions to affect the ionic concentration significantly (a drop in the ocean) so we can ignore their effects. • Actual ionic concentrations in mammalian neurons: Ion Internal concentration External concentration Valence (z) Equilibrium potential Na+ 15 mM 150 mM +1 +62 mV K+ 150 mM 5.5 mM +1 –89 mV Cl– 9 mM 125 mM –1 –71 mV Ca2+ 10–4 mM 1 mM +2 +124 mV • Equilibrium potential for each ion is determined solely by the concentration gradient and valence, by the Nernst equation: E = –1 –1 (RT/zF) ln(concout/concin). R is the gas constant (8.314 J deg mol ); T is the absolute temperature (37°C = 310 K); z is the va- lence for the ion; F is Faraday’s constant (96500 C mol–1); E is in volts. • Remember that an ion will not flow across a membrane if the potential gradient equals that ion’s equilibrium potential (by defi- nition). • The resting potential is determined by the equilibrium potentials for every ion to which the membrane is permeable, weighted + + – + + by the permeability (p), via th Goldman equation: E = (RT/F) ln[ (pK[K ]out + pNa[Na ]out + pCl[Cl ]in) / (pK[K ]in + pNa[Na ]in + – pCl[Cl ]out)].
    [Show full text]
  • The Cells That Make Us Who We Are How Neurons Communicate With
    Communication within the Nervous System The Cells that make us who we are How neurons communicate with one another Garrett: Brain & Behavior 4e 1 The Cells That Make Us Who We Are • How many are there? • Neurons: 100 billion • Make up 10% of brain volume • Glia: Many more! • Make up 90% of brain volume • Neurons: Jobs include • convey sensory information to the brain; • carry out operations involved in thought and feeling; • Send commands out to the body. • Dendrites • Cell body or soma Garrett: Brain & Behavior 4e • Axons insulated with myelin (secreted by glia), with end terminals that release neurotransmitters from vesicles into the synapse 2 The Cells That Make Us Who We Are Figure 2.3: Components of a Neuron Garrett: Brain & Behavior 4e 3 The Cells That Make Us Who We Are Figure 2.4 a,b : The Three Shapes of Neurons • Unipolar neurons (a) • Bipolar neurons (b) • Multipolar neurons • Figure 2 .3, previous slide Garrett: Brain & Behavior 4e 4 The Cells That Make Us Who We Are Table 2.1: The Three Types of Neurons Figure 2.4c: The Three Shapes of Neurons Type Shape Description Motor neuron Multipolar Output to muscles/organs Sensory neuron Unipolar or Bipolar Input from receptors Interneuron Multipolar Most within the CNS. Most common. Garrett: Brain & Behavior 4e 5 The Cells That Make Us Who We Are Figure 2.5: Composition of the Cell Membrane • Lipids • Heads attracted to water in and outside the cell, tails repelled by water • Creates a double-layer membrane • Proteins • Hold the cells together • Controls the environment in and around the cell Garrett: Brain & Behavior 4e 6 The Neural Membrane • The neuron has a selectively-permeable membrane.
    [Show full text]
  • NEURON and the PHYSIOLOGY of NERVE IMPULSE the Nervous
    NEURON AND THE PHYSIOLOGY OF NERVE IMPULSE The nervous system is made of millions of structural and functional units called nerve cell or neurons and a number of supporting cells called glial cells. The function of the nerve cell is to receive and transmit impulses or messages and integrate the entire body as a single unit. The neurons can be classified into three types – 1. Unipolar neuron- it has a cell body or cyton from which arises a single short branch called neurite that immediately divides into the dendritic or receiving branch and axonic or transmitting branch. 2. Bipolar neuron- The neuron has the cell body from which arises two neurites called the dendron and the axon respectively. 3. Multipolar neuron- From the cell body arise many dendrites and one long axon. Neurons can also be classified into 1) myelinated when myelin sheath surrounds the axon and 2) non-myelinated neurons when the axon is naked and not covered by the myelin sheath. 1 Structure of a myelinated neuron/nerve cell The neuron can be divided into three parts-cell body or cyton from which arises two types of branches, i.e., many branched processes called dendrons and a long unbranched process called axon. The cyton or cell body is filled with the cytoplasm also called neuroplasm that is limited by the plasma membrane. It contains the nucleus, mitochondria, endoplasmic reticulum, golgi bodies, neurofibrils (filaments that act as a cytoskeleton) and special dense RNA rich granules called Nissl’s granules (help in protein synthesis). The dendrons terminate in slender processes called dendrites.
    [Show full text]
  • 1) the Resting Membrane Potential Is: A) 0 Mv, Charge Is Balanced at Rest
    1) The resting membrane potential is: a) 0 mV, charge is balanced at rest b) Negative inside because potassium can diffuse out of the cell c) Negative inside because Cl- concentrations are higher inside the cell d) Negative outside because sodium can diffuse into the cell 2) Which of the following is a true statement about cells in the resting state : a) Chloride moves into the cells because the concentration of chloride is higher inside the cell than outside the cell b) Large anions (A-) moves out of the cell because it has a higher concentration inside the cell than outside the cell c) Sodium moves into the cell because it has a higher concentration outside the cell than inside the cell d) Voltage gated sodium channels are closed 3) The action potential threshold stimulus causes: a) chloride to enter the cell b) Voltage gated sodium and potassium channels to open c) Voltage gated sodium channels to inactivate d) Release of Ca++ from the axon 4) Cardiac muscle: a) Is striated b) Has no electrical connection between cells c) Is not striated d) Has cells that are long and unbranched 5) This causes vesicles to migrate and release of neurotransmitter in the chemical synapse: a) Increased dopamine b) Monoamine oxidase c) Increased calcium d) Increased potassium 6) Prozac increases the amount of serotonin present in the synapse by: a) Acting as a selective serotonin reuptake inhibitor b) Increasing tryptophan levels c) Blocking the enzymatic degradation of serotonin d) Increasing serotonin synthesis 7) When the sarcomere shortens: a) Calcium levels decrease b) Myosin pulls on the actin filament c) ATP must not be present d) Potassium is bound to troponin 8) This negatively charged ion is found at high concentrations (i.e., 120 mM) outside the cell: a) Sodium b) A- c) Chloride d) Bicarbonate 9) Excitable cells such as neurons a) Have a resting membrane potential of around +35 mV b) Have a resting membrane potential of around -70 mV c) Have internal potassium concentrations that are the same as potassium concentrations outside the cell.
    [Show full text]
  • Hyperkalemia and Hypocalcemia - Literature Review Modalidades De Parada Cardíaca Induzida: Hipercalemia E Hipocalcemia - Revisão De Literatura
    Oliveira MAB,SPECIAL et al. - Modes ARTICLE of induced cardiac arrest: hyperkalemia and Rev Bras Cir Cardiovasc 2014;29(3):432-6 hypocalcemia - Literature review Modes of induced cardiac arrest: hyperkalemia and hypocalcemia - Literature review Modalidades de parada cardíaca induzida: hipercalemia e hipocalcemia - revisão de literatura Marcos Aurélio Barboza de Oliveira1, MD, MsC; Antônio Carlos Brandi2, MD; Carlos Alberto dos Santos2, MD; Paulo Henrique Husseini Botelho2, MD; José Luis Lasso Cortez3, MD; Domingo Marcolino Braile4, MsC, PhD DOI: 10.5935/1678-9741.20140074 RBCCV 44205-1572 Abstract Resumo The entry of sodium and calcium play a key effect on myocyte A entrada de sódio e cálcio desempenham efeito chave no miócito subjected to cardiac arrest by hyperkalemia. They cause cell submetido à parada cardíaca por hiperpotassemia. Eles provocam swelling, acidosis, consumption of adenosine triphosphate and edema celular, acidose, consumo de trifosfato de adenosina e desen- trigger programmed cell death. Cardiac arrest caused by hypo- cadeiam processo de morte celular programada. A parada cardíaca calcemia maintains intracellular adenosine triphosphate levels, provocada por hipocalcemia mantém os níveis intracelulares de improves diastolic performance and reduces oxygen consumption, trifosfato de adenosina, melhora o rendimento diastólico e reduz o which can be translated into better protection to myocyte injury consumo de oxigênio, o que pode ser traduzido em melhor proteção induced by cardiac arrest. do miócito às lesões provocadas pela parada cardíaca induzida. Descriptors: Heart Arrest, Induced. Myocardial Ischemia. Descritores: Parada Cardíaca Induzida. Isquemia Miocárdi- Hyperkalemia. Hypocalcemia. ca. Hiperpotassemia. Hipocalcemia. INTRODUCTION to approach intracardiac diseases[3] by using substances that trigger controlled cardiac arrest, commonly known as cardio- The first cardiac surgeries were performed on a beating plegic agents [4].
    [Show full text]