DOCSLIB.ORG

Chapter 2 Introduction Additional Resources

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2 Introduction Additional Resources SCIENTIFIC MEASUREMENT AND DIMENSIONAL ANALYSIS Chapter 2 Memorise Understand Importance * SI units and prefixes * Dimensional analysis High level: 11% of GAMSAT Section 3 maths-based questions released by ACER are related to content in this chapter (in our estimation). * Note that approximately 90% of such questions are related to just 3 chapters: 1, 2, and 3. Introduction It is extremely important to know the SI system of measurement for the GAMSAT. The metric system is very much related to the SI system. The British system, though familiar, does not need to be memorised for the GAMSAT (related questions would only be asked if relevant conversion factors were provided). 'Dimensional analysis' is a technique whereby simply paying attention to units and applying the basic algebra we covered in GM Chapter 1, you will be able to solve several real exam questions in GAMSAT Physics, Chemistry and Biology – even without previous knowledge in those subjects. Additional Resources Open Discussion Boards Special Guest GAMSAT MATHS GM-37 2.0 Yes, GAMSAT Has a Need for Speed! A ‘unit’ is any standard used for Physics easier. It is normal if you cannot fill making comparisons in measurements. out the tables now, but please return to this Units form an important part of the founda- page after you have studied this chapter so tion of science and GAMSAT Section 3. you can complete all entries below. For non-science students, this is a Science students? Do your best, be new language to learn but the vocabulary quick, note that some entries that appear is incredibly small. The units below can all simple may surprise you! ACER has exam be found in this chapter, and throughout questions directly dependent on your GAMSAT Physics and Chemistry. Your famil- understanding of SI units and prefixes, so High-level Importance iarity with these units will make your study of let’s get started… Section Units 2.1.3 length: electric current: Table 1: SI Base mass: thermodynamic temperature: Units time: amount of substance: Section Units 2.1.3 area: speed, velocity: Table 2: Examples volume: acceleration: of SI Derived Units Section Units 2.1.3 frequency: power: Table 3: SI electric charge, quantity force: of electricity: Derived Units with Special Names electric potential difference, pressure, stress: electromotive force: and Symbols energy, work, quantity of heat: Section Base 10 tera: deci: 2.1.3 giga: centi: Table 4: Important mega: milli: SI prefixes for GAMSAT, A closer kilo: micro: look hecto: nano: deca: pico: GM-38 Chapter 2: SCIENTIFIC MEASUREMENT AND DIMENSIONAL ANALYSIS GAMSAT MASTERS SERIES 2.1 Systems of Measurement High-level Importance 2.1.1 British Units (Imperial System of Measurement) You are probably already familiar with Minutes There are 60 seconds in several of these units of measurement, but we every minute. 1 min. = 60 s. recommend reviewing them at least once. Hours There are 60 minutes in every A. Length: These units are used to hour. 1 h. = 60 min. describe things like the length of physi- cal objects, the displacement of a physical Days There are 24 hours in every object, the distance something has traveled day. 1 day = 24 h. or will travel, etc. Area and volume are also measured as the square and cube (respec- Years The year is the largest unit tively) of these units. of time in the British System. There are 365 days in every Inches The inch is the smallest year. 1 yr. = 365 days measurement of length in the British System. C. Mass/Weight: These terms are not Feet There are 12 inches in every technically the same and we will discuss the foot. 1 ft. = 12 in. differences in Physics. The following units describe the amount of matter in an object. Yards There are 3 feet in every yard. 1 yd. = 3 ft. Ounces The ounce is the smallest unit of mass in the British System. Miles The mile is the largest unit of length in the British System. Pounds There are 16 ounces (oz.) in There are 5,280 feet in every every pound (lb.). 1 lb. = 16 oz. mile. 1 mi. = 5,280 ft. Tons The ton is the largest unit of mass in the British System. B. Time: These units describe the passage There are 2,000 lbs. in an of time. American ton, and 2,240 lbs. in a British tonne. Neither Seconds The second is the smallest unit should be committed to of time in the British System. memory. GAMSAT MATHS GM-39 2.1.2 Metric Units Measuring with Powers of 10: Unlike As you go down, you divide by 10 and the British System, the Metric System has as you go up, you multiply by 10 in order to only one unit for each category of measure- convert between the units. ment. In order to describe quantities that are much larger or much smaller than one EXAMPLE of the base units, a prefix is chosen from a How many metres is 1 kilometre? variety of options and added to the front of High-level Importance the unit. This changes the value of the unit 1 km = 1000 m by some power of 10, which is determined by what the prefix is. The following are the From general knowledge, we know most common of these prefixes (with the that kilo means one thousand. This means representative symbols in brackets): there are 1000 metres in a kilometre. But just in case you get confused, you can also - use the clue from the mnemonic. Now we Milli (m) One thousandth (10 3) of the know that Kilo is three slots upward from base unit the Unit base. Hence we multiply 3 times by - 10: 10 × 10 × 10 = 1000. Centi (c) One hundredth (10 2) of the base unit An even less confusing way to figure out how to do the metric conversions quickly and One tenth (10-1) of the base Deci (d) accurately, is to use a metric conversion line. unit This is quite handy with any of the common units such as the metre, litre, and grams. Deca (da) Ten (101) times the base unit Kilo (k) One thousand (103) times the K H D U D C M base unit There is a mnemonic that may be m l used to identify these prefixes: g King Kilometre Kilo Henry Hectometre Hecto (h) Figure GM 2.1: The Metric Conversion Died Decametre Deca Line. The letters on top of the metric line Unexpectedly Unit Base Unit stands for the “King Henry” mnemonic. On Drinking Decimetre Deci the other hand, the letters below the metric line - m, l, g – stand for the unit bases, metre, Chocolate Centimetre Centi litre, or gram, respectively. Milk Milimetre Milli GM-40 Chapter 2: SCIENTIFIC MEASUREMENT AND DIMENSIONAL ANALYSIS GAMSAT MASTERS SERIES To use this device, draw out the Now, let’s try converting centimetre to metric line as shown in Fig GM 2.1. From kilometre: What is 6.3 cm in km? the centremost point U, the prefixes going High-level Importance to the left represent those that are larger 1. Place your pen on the c (centi) point than the base unit (kilo, hecto). These also in the metric line. correspond to the decimal places that you will be moving from the numerical value of 2. Moving from c to k (kilo) takes five the unit to be converted. Those going to places going to the left. This also the right are for the ones smaller than the means moving five places from the unit (deci, centi, milli). decimal point of the number 6.3. 6.3 cm = .000063 km EXAMPLE Using this method definitely makes doing the metric conversions so much How much is 36 litres in millilitres? faster than the fraction method! Step 1: Place your pen on the given unit, in this case L (litre). Then count the There are other prefixes that are often number of places it takes you to reach the used scientifically: unit being asked in the problem (millilitre). Tera (T) 1012 times the base unit Giga (G) 109 times the base unit 6 k h d u d c m Mega (M) 10 times the base unit Micro (μ) 10-6 of the base unit Nano (n) 10-9 of the base unit Pico (p) 10-12 of the base unit L A. Length: As with British length units, : Converting litre to millilitre Fig GM 2.2 these are used to measure anything that has using the metric conversion line. to do with length, displacement, distance, etc. Area and volume are also measured as the Step 2: Because it took you three places square and cube (respectively) of these units. going to the right to move from the litre to the millilitre units, you also need to add Metres The metre is the basic unit of three places from the decimal point of the length in the Metric System. number 36.0. Other millimetre, centimetre, 36 L = 36,000 ml Common kilometre Forms GAMSAT MATHS GM-41 B. Time: These are units that quantify the C. Mass: These are units that describe passage of time. the amount of matter in an object. Seconds Just as in the British System, Grams The gram is the basic metric the second is the basic unit unit of mass. of time in the Metric System. Minutes, hours, and the other Other milligram, kilogram British units are not technically Common part of the Metric System, but Forms they are often used anyway in High-level Importance problems involving metric units. Other millisecond Common Forms 2.1.3 SI Units SI units is the International System of Units (abbreviated SI from the French NOTE Le Système International d'Unités) and is a modern form of the metric system.
Load more

Recommended publications
  • M Motion Intervention Booklet.Pdf (810.7KB)
    Motion Intervention Booklet 1 Random uncertainties have no pattern. They can cause a reading to be higher or lower than the “true value”. Systematic uncertainties have a pattern. They cause readings to be consistently too high or consistently too low. 2 The uncertainty in repeat readings is found from “half the range” and is given to 1 significant figure. Time / s Trial 1 Trial 2 Trial 3 Mean 1.23 1.20 1.28 Mean time = 1.23 + 1.20 + 1.28 = 1.23666666 => 1.24 (original data is to 2dp, so 3 the mean is to 2 dp as well) Range = 1.20 1.28. Uncertainty is ½ × (1.28 – 1.20) = ½ × 0.08 = ± 0.04 s 3 The speed at which a person can walk, run or cycle depends on many factors including: age, terrain, fitness and distance travelled. The speed of a moving object usually changes while it’s moving. Typical values for speeds may be taken as: walking: 1.5 m/s running: 3 m/s cycling: 6 m/s sound in air: 330 m/s 4 Scalar quantities have magnitude only. Speed is a scaler, eg speed = 30 m/s. Vector quantities have magnitude and direction. Velocity is a vector, eg velocity = 30 m/s north. Distance is how far something moves, it doesn’t involve direction. The displacement at a point is how far something is from the start point, in a straight line, including the direction. It doesn’t make any difference how far the object has moved in order to get to that point.
    [Show full text]
  • CAR-ANS PART 05 Issue No. 2 Units of Measurement to Be Used In
    CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES Part 5 Governing UNITS OF MEASUREMENT TO BE USED IN AIR AND GROUND OPERATIONS CIVIL AVIATION AUTHORITY OF THE PHILIPPINES Old MIA Road, Pasay City1301 Metro Manila INTENTIONALLY LEFT BLANK CAR-ANS PART 5 Republic of the Philippines CIVIL AVIATION REGULATIONS AIR NAVIGATION SERVICES (CAR-ANS) Part 5 UNITS OF MEASUREMENTS TO BE USED IN AIR AND GROUND OPERATIONS 22 APRIL 2016 EFFECTIVITY Part 5 of the Civil Aviation Regulations-Air Navigation Services are issued under the authority of Republic Act 9497 and shall take effect upon approval of the Board of Directors of the CAAP. APPROVED BY: LT GEN WILLIAM K HOTCHKISS III AFP (RET) DATE Director General Civil Aviation Authority of the Philippines Issue 2 15-i 16 May 2016 CAR-ANS PART 5 FOREWORD This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was formulated and issued by the Civil Aviation Authority of the Philippines (CAAP), prescribing the standards and recommended practices for units of measurements to be used in air and ground operations within the territory of the Republic of the Philippines. This Civil Aviation Regulations-Air Navigation Services (CAR-ANS) Part 5 was developed based on the Standards and Recommended Practices prescribed by the International Civil Aviation Organization (ICAO) as contained in Annex 5 which was first adopted by the council on 16 April 1948 pursuant to the provisions of Article 37 of the Convention of International Civil Aviation (Chicago 1944), and consequently became applicable on 1 January 1949. The provisions contained herein are issued by authority of the Director General of the Civil Aviation Authority of the Philippines and will be complied with by all concerned.
    [Show full text]
  • SI Base Units
    463 Appendix I SI base units 1 THE SEVEN BASE UNITS IN THE INTERNatioNAL SYSTEM OF UNITS (SI) Quantity Name of Symbol base SI Unit Length metre m Mass kilogram kg Time second s Electric current ampere A Thermodynamic temperature kelvin K Amount of substance mole mol Luminous intensity candela cd 2 SOME DERIVED SI UNITS WITH THEIR SYMBOL/DerivatioN Quantity Common Unit Symbol Derivation symbol Term Term Length a, b, c metre m SI base unit Area A square metre m² Volume V cubic metre m³ Mass m kilogram kg SI base unit Density r (rho) kilogram per cubic metre kg/m³ Force F newton N 1 N = 1 kgm/s2 Weight force W newton N 9.80665 N = 1 kgf Time t second s SI base unit Velocity v metre per second m/s Acceleration a metre per second per second m/s2 Frequency (cycles per second) f hertz Hz 1 Hz = 1 c/s Bending moment (torque) M newton metre Nm Pressure P, F newton per square metre Pa (N/m²) 1 MN/m² = 1 N/mm² Stress σ (sigma) newton per square metre Pa (N/m²) Work, energy W joule J 1 J = 1 Nm Power P watt W 1 W = 1 J/s Quantity of heat Q joule J Thermodynamic temperature T kelvin K SI base unit Specific heat capacity c joule per kilogram degree kelvin J/ kg × K Thermal conductivity k watt per metre degree kelvin W/m × K Coefficient of heat U watt per square metre kelvin w/ m² × K 464 Rural structures in the tropics: design and development 3 MUltiples AND SUB MUltiples OF SI–UNITS COMMONLY USED IN CONSTRUCTION THEORY Factor Prefix Symbol 106 mega M 103 kilo k (102 hecto h) (10 deca da) (10-1 deci d) (10-2 centi c) 10-3 milli m 10-6 micro u Prefix in brackets should be avoided.
    [Show full text]
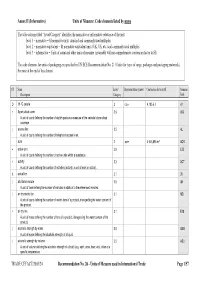
  • Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
    Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product.
    [Show full text]
  • Beyond the Metre (Part II)
    Iowa Science Teachers Journal Volume 17 Number 2 Article 10 1980 Beyond the Metre (Part II) Richard S. Thompkins Mississippi Bend Area Education Agency Vincent N. Lunetta University of Iowa Follow this and additional works at: https://scholarworks.uni.edu/istj Part of the Science and Mathematics Education Commons Let us know how access to this document benefits ouy Copyright © Copyright 1980 by the Iowa Academy of Science Recommended Citation Thompkins, Richard S. and Lunetta, Vincent N. (1980) "Beyond the Metre (Part II)," Iowa Science Teachers Journal: Vol. 17 : No. 2 , Article 10. Available at: https://scholarworks.uni.edu/istj/vol17/iss2/10 This Article is brought to you for free and open access by the Iowa Academy of Science at UNI ScholarWorks. It has been accepted for inclusion in Iowa Science Teachers Journal by an authorized editor of UNI ScholarWorks. For more information, please contact [email protected]. BEYOND THE METRE (Part II) Richard S. Tompkins Metric Education Consultant Mississippi Bend Area Education Agency 2604 West Locust Street Davenport, Iowa 52804 Vincent N. Lunetta Associate Professor of Science Education University of Iowa Iowa City, Iowa 52242 Introduction This article is the second in a series discussing the wide spectrum of metric units. The first article dealt with some general aspects of the International System of Units (SI) and then went on to consider the metre, square metre, cubic metre and second. This article describes the SI unit of mass, and how units for velocity and acceleration are built using physical laws. The Metre Per Second (mis) Speed is usually represented in terms of a distance traveled during some time interval.
    [Show full text]
  • Units of Measurement to Be Used in Air and Ground Operations
    International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices,see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Suzanne TRANSMITTAL NOTE NEW EDITIONS OF ANNEXES TO THE CONVENTION ON INTERNATIONAL CIVIL AVIATION It has come to our attention that when a new edition of an Annex is published, users have been discarding, along with the previous edition of the Annex, the Supplement to the previous edition. Please note that the Supplement to the previous edition should be retained until a new Supplement is issued. Suzanne International Standards and Recommended Practices Annex 5 to the Convention on International Civil Aviation Units of Measurement to be Used in Air and Ground Operations ________________________________ This edition incorporates all amendments adopted by the Council prior to 23 February 2010 and supersedes, on 18 November 2010, all previous editions of Annex 5. For information regarding the applicability of the Standards and Recommended Practices, see Foreword. Fifth Edition July 2010 International Civil Aviation Organization Published in separate English, Arabic, Chinese, French, Russian and Spanish editions by the INTERNATIONAL CIVIL AVIATION ORGANIZATION 999 University Street, Montréal, Quebec, Canada H3C 5H7 For ordering information and for a complete listing of sales agents and booksellers, please go to the ICAO website at www.icao.int First edition 1948 Fourth edition 1979 Fifth edition 2010 Annex 5, Units of Measurement to be Used in Air and Ground Operations Order Number: AN 5 ISBN 978-92-9231-512-2 © ICAO 2010 All rights reserved.
    [Show full text]
  • Units of Measurement to Be Used in Air and Ground Operations
    Manual of Standards - Units of Measurement to be used in Air and Ground Operations Version 1.1 : 18 November 2010 published by Civil Aviation Authority of Singapore INTENTIONALLY LEFT BLANK MOS – Units of Measurement to be used in Air and Ground Operations Table of Contents TABLE OF CONTENTS AMENDMENT RECORDS ii FOREWORD ii Chapter 1 Definitions 1-1 Chapter 2 Applicability 2-1 Chapter 3 Standard Application of Units of Measurement 3-1 Chapter 4 Termination of use of Non-SI Units 4-1 List of Tables Table 3-1: SI unit prefixes 3-1 Table 3-2: Non-SI units for use with the SI 3-2 Table 3-3: Non-SI units permitted for temporary use with the SI 3-3 Table 3-4: Standard application of specific units of measurement 3-3 Table 3-5: Temperature conversion formulae 3-7 Table 4-1: Termination dates for non-SI units 4-1 Version 1.1 : 18 November 2010 i MOS – Units of Measurement to be used in Air and Ground Operations Amendment Records AMENDMENT RECORDS The amendments listed below have been incorporated into this copy of the Manual of Standards – Units of Measurement to be used in Air and Ground Operations. Amendment Version Subject Source Sections affected Entered by Approved by Effective no. no. date (Date) (Date) - 1.0 Original version - All AAR Chief Executive 1 July 2010 (1 July 2010) (1 July 2010) 1 1.1 Unit for wind speed ICAO Annex 5 4.16 in Table 3-4 AAR Chief Executive 18 Nov 2010 (incorporating (1 Nov 2010) (1 Nov 2010) Amendment 17 applicable on 18 Nov 2010) Version 1.1 : 18 November 2010 ii MOS – Units of Measurement to be used in Air and Ground Operations Foreword FOREWORD Pursuant to paragraph 88(C) of the Air Navigation Order (ANO), this Manual of Standards – Units of Measurement to be used in Air and Ground Operations is issued by CAAS to specify the use of a standardized system of units of measurement in international civil aviation air and ground operations.
    [Show full text]
  • Units and Conversions the Metric System Originates Back to the 1700S in France
    Numeracy Introduction to Units and Conversions The metric system originates back to the 1700s in France. It is known as a decimal system because conversions between units are based on powers of ten. This is quite different to the Imperial system of units where every conversion has a unique value. A physical quantity is an attribute or property of a substance that can be expressed in a mathematical equation. A quantity, for example the amount of mass of a substance, is made up of a value and a unit. If a person has a mass of 72kg: the quantity being measured is Mass, the value of the measurement is 72 and the unit of measure is kilograms (kg). Another quantity is length (distance), for example the length of a piece of timber is 3.15m: the quantity being measured is length, the value of the measurement is 3.15 and the unit of measure is metres (m). A unit of measurement refers to a particular physical quantity. A metre describes length, a kilogram describes mass, a second describes time etc. A unit is defined and adopted by convention, in other words, everyone agrees that the unit will be a particular quantity. Historically, the metre was defined by the French Academy of Sciences as the length between two marks on a platinum-iridium bar at 0°C, which was designed to represent one ten-millionth of the distance from the Equator to the North Pole through Paris. In 1983, the metre was redefined as the distance travelled by light 1 in free space in of a second.
    [Show full text]
  • Implementing a Physical Units Library for C++
    Implementing a Physical Units Library for C++ Mateusz Pusz April 12, 2019 Famous motivating example The Mars Climate Orbiter • Robotic space probe launched by NASA on December 11, 1998 ACCU 2019 | Implementing a Physical Units Library for C++ 3 The Mars Climate Orbiter • Robotic space probe launched by NASA on December 11, 1998 • Project costs: $327.6 million – spacecra development: $193.1 million – launching it: $91.7 million – mission operations: $42.8 million ACCU 2019 | Implementing a Physical Units Library for C++ 3 The Mars Climate Orbiter • Robotic space probe launched by NASA on December 11, 1998 • Project costs: $327.6 million – spacecra development: $193.1 million – launching it: $91.7 million – mission operations: $42.8 million • Mars Climate Orbiter began the planned orbital insertion maneuver on September 23, 1999 at 09:00:46 UTC ACCU 2019 | Implementing a Physical Units Library for C++ 3 The Mars Climate Orbiter • Space probe went out of radio contact when it passed behind Mars at 09:04:52 UTC, 49 seconds earlier than expected • Communication was never reestablished • The spacecra disintegrated due to atmospheric stresses ACCU 2019 | Implementing a Physical Units Library for C++ 6 What went wrong? ACCU 2019 | Implementing a Physical Units Library for C++ 7 What went wrong? • The primary cause of this discrepancy was that – one piece of ground soware supplied by Lockheed Martin produced results in a United States customary unit, contrary to its Soware Interface Specification (SIS) – second system, supplied by NASA, expected
    [Show full text]
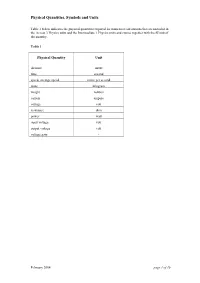
  • Quantity Symbol Sheet
    Physical Quantities, Symbols and Units Table 1 below indicates the physical quantities required for numerical calculations that are included in the Access 3 Physics units and the Intermediate 1 Physics units and course together with the SI unit of the quantity. Table 1 Physical Quantity Unit distance metre time second speed, average speed metre per second mass kilogram weight newton current ampere voltage volt resistance ohm power watt input voltage volt output voltage volt voltage gain - February 2004 page 1 of 10 Physical Quantities, Symbols and Units Table 2 below indicates the physical quantities required for numerical calculations that are included in the Standard Grade Physics course together with: • the symbol used by SQA • the SI unit of the quantity (and alternative units included in the course) • the abbreviation for the unit used in Credit level examinations. In General level examinations full words are used for the units of all physical quantities. Table 2 Physical Quantity Symbol Unit Unit Abbreviation distance d or s metre m light year height h metre m wavelength λ metre m amplitude Α metre m time t second s speed, final speed v metre per second m/s initial speed u metre per second m/s change of speed ∆v metre per second m/s average speed v metre per second m/s frequency f hertz Hz acceleration a metre per second per second m/s2 acceleration due to gravity g metre per second per second m/s2 gravitational field strength g newton per kilogram N/kg mass m kilogram kg weight W newton N force, thrust F newton N energy E joule
    [Show full text]
  • SI QUICK REFERENCE GUIDE: International System of Units (SI) the Modernized Metric System*
    SI QUICK REFERENCE GUIDE: International System of Units (SI) The Modernized Metric System* UNITS The International System of Units (SI) is based on seven fundamental (base) units: Base Units Quantity Name Symbol length metre m mass kilogram kg time second s electric current ampere A thermodynamic temperature kelvin K amount of substance mole mol luminous intensity candela cd and a number of derived units which are combinations of base units and which may have special names and symbols: Examples of Derived Units Quantity Expression Name Symbol acceleration angular rad/s2 linear m/s2 angle plane dimensionless radian rad solid dimensionless steradian sr area m2 Celsius temperature K degree Celsius °C density heat flux W/ m2 mass kg/m3 current A/m2 energy, enthalpy work, heat N • m joule J specific J/ kg entropy heat capacity J/ K specific J/ (kg•K) flow, mass kg/s flow, volume m3/s force kg • m/s2 newton N frequency periodic 1/s hertz Hz rotating rev/s inductance Wb/A henry H magnetic flux V • s weber Wb mass flow kg/s moment of a force N • m potential,electric W/A volt V power, radiant flux J/s watt W pressure, stress N/m2 pascal Pa resistance, electric V/A ohm Ω thermal conductivity W/(m • K) velocity angular rad/s linear m/s viscosity dynamic (absolute)(µ)Pa• s kinematic (ν)m2/s volume m3 volume, specific m3/kg *For complete information see IEEE/ASTM SI-10. SI QUICK REFERENCE GUIDE SYMBOLS Symbol Name Quantity Formula A ampere electric current base unit Bq becquerel activity (of a radio nuclide) 1/s C coulomb electric charge A • s °C
    [Show full text]
  • Using SI Units Calculation Sheet Physics
    Using SI Units Physics Calculation sheet Using SI units Specification references • 3.1.1 Use of SI units and their prefixes • M0.1 Recognise and make use of appropriate units in calculations Maths Skills for Physics references • 1.1 Units and dimensions Learning objectives After completing the worksheet you should be able to: • show knowledge and understanding of base and derived SI units • use equations to work out derived units • use base units to check homogeneity of equations. Introduction Base quantities are measured in base units. These are units that are not based on other units. For example, mass is measured in kilograms and length is measured in metres. Other quantities have units which are derived from the base quantities. For example, the unit of density (kg m–3) is derived from the kilogram and the metre. The first example shows you how to use an equation to work out the unit of a derived quantity. The second example shows you how to check that an equation is homogeneous or, in other words, that its units are balanced. Worked example Question What is the SI unit of speed? Answer Step 1 Identify the equation to use. Speed is defined as: Step 2 Write the equation in terms of units. The SI unit of speed is defined as: © Oxford University Press 2015 www.oxfordsecondary.co.uk/acknowledgements This resource sheet may have been changed from the original 1 Using SI Units Physics Calculation sheet Step 3 Select the appropriate SI base units. SI unit of distance = metre (m) SI unit of time = second (s) Step 4 Insert the SI base units into the equation.
    [Show full text]