From Gallons to Miles: a Disaggregate Analysis of Automobile Travel and Externality Taxes☆
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lesson 1: Length English Vs
Lesson 1: Length English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer B. 1 yard or 1 meter C. 1 inch or 1 centimeter English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 yard = 0.9444 meters English vs. Metric Units Which is longer? A. 1 mile or 1 kilometer 1 mile B. 1 yard or 1 meter C. 1 inch or 1 centimeter 1.6 kilometers 1 inch = 2.54 centimeters 1 yard = 0.9444 meters Metric Units The basic unit of length in the metric system in the meter and is represented by a lowercase m. Standard: The distance traveled by light in absolute vacuum in 1∕299,792,458 of a second. Metric Units 1 Kilometer (km) = 1000 meters 1 Meter = 100 Centimeters (cm) 1 Meter = 1000 Millimeters (mm) Which is larger? A. 1 meter or 105 centimeters C. 12 centimeters or 102 millimeters B. 4 kilometers or 4400 meters D. 1200 millimeters or 1 meter Measuring Length How many millimeters are in 1 centimeter? 1 centimeter = 10 millimeters What is the length of the line in centimeters? _______cm What is the length of the line in millimeters? _______mm What is the length of the line to the nearest centimeter? ________cm HINT: Round to the nearest centimeter – no decimals. -

Fuel Efficiency: Modes of Transportation Ranked by MPG | True Cost
Fuel Efficiency: Modes of Transportation Ranked By MPG | True Cost -... http://truecostblog.com/2010/05/27/fuel-efficiency-modes-of-transportati... Fuel Efficiency: Modes of Transportation Ranked By MPG May 27, 2010 at 4:57 pm ∙ Filed under Energy, Environment, Ideas ∙Tagged bicycle mpg, fuel efficiency, running mpg, transportation, walking mpg Building on a previous post on the energy efficiency of various foods, I decided to create a list of transportation modes by fuel efficiency. In order to compare vehicles with different passenger capacities and average utilization, I included both average efficiency and maximum efficiency, at average and maximum passenger loads. The calculations and source data are explained in detail in the footnotes. For human‐powered activities, the mpg ratings might appear high, but many calculations omit the fact that a human’s baseline calorie consumption must be subtracted to find the efficiency of human‐powered transportation. I have subtracted out baseline metabolism, showing the true efficiencies for walking, running, and biking. For vehicles like trucks and large ships which primarily carry cargo, I count 4000 pounds of cargo as equivalent to one person. This is roughly the weight of an average American automobile (cars, minivans, SUVs, and trucks). The pmpg ratings of cars, trucks, and motorcycles are also higher than traditional mpg estimates, since pmpg accounts for the average number of occupants in a vehicle, which according to the Bureau of Transportation Statistics is 1.58 for cars, 1.73 for SUVs, minivans, and trucks, and 1.27 for motorcycles. List of Transportation Modes By Person‐Miles Per Gallon (PMPG) Transport Average PMPG Max PMPG Bicycle [3] 984 984 Walking [1] 700 700 Freight Ship [10] 340 570 Running [2] 315 315 Freight Train [7] 190.5 190.5 Plugin Hybrid [5] 110.6 350 Motorcycle [4] 71.8 113 Passenger Train [7] 71.6 189.7 Airplane [9] 42.6 53.6 Bus [8] 38.3 330 Car [4] 35.7 113 18‐Wheeler (Truck) [5] 32.2 64.4 Light Truck, SUV, Minivan [4] 31.4 91 [0] I used these conversion factors for all calculations. -

Yd.) 36 Inches = 1 Yard (Yd.) 5,280 Feet = 1 Mile (Mi.) 1,760 Yards = 1 Mile (Mi.)
Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com 1. Find the greatest length. 2. Find the greatest length. 9 in. or 1 ft. 3 ft. or 39 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 3. Find the greatest length. 4. Find the greatest length. 1 ft. 7 in. or 18 in. 4 ft. 4 in. or 55 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 5. Find the greatest length. 6. Find the greatest length. 1 ft. 9 in. or 2 ft. 7 ft. or 2 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 7. Find the greatest length. 8. Find the greatest length. 26 in. or 2 ft. 6 yd. or 17 ft. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 9. Find the greatest length. 10. Find the greatest length. 5 ft. or 1 ½ yd. 112 in. or 3 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 11. Find the greatest length. 12. Find the greatest length. 99 in. or 3 yd. 11,000 ft. or 2 mi. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 13. -

Useful Forestry Measurements Acre: a Unit of Area Equaling 43,560
Useful Forestry Measurements Acre: A unit of area equaling 43,560 square feet or 10 square chains. Basal Area: The area, usually in square feet, of the cross-section of a tree stem near its base, generally at breast height and inclusive of bark. The basal area per acre measurement gives you some idea of crowding of trees in a stand. Board Foot: A unit of area for measuring lumber equaling 12 inches by 12 inches by 1 inch. Chain: A unit of length. A surveyor’s chain equals 66 feet or 1/80-mile. Cord: A pile of stacked wood measuring 4 feet by 4 feet by 8 feet when originally conceived. Cubic Foot: A unit of volume measure, wood equivalent to a solid cube that measures 12 inches by 12 inches by 12 inches or 1,728 cubic inches. Cunit: A volume of wood measuring 3 feet and 1-1/2 inches by 4 feet by 8 feet and containing 100 solid cubic feet of wood. D.B.H. (diameter breast height): The measurement of a tree’s diameter at 4-1/2 feet above the ground line. M.B.F. (thousand board feet): A unit of measure containing 1,000 board feet. Section: A unit of area containing 640 acres or one square mile. Square Foot: A unit of area equaling 144 square inches. Township: A unit of land area covering 23,040 acres or 36 sections. Equations Cords per acre (based on 10 Basal Area Factor (BAF) angle gauge) (# of 8 ft sticks + # of trees)/(2 x # plots) Based on 10 Basal Area Factor Angle Gauge Example: (217+30)/(2 x 5) = 24.7 cords/acre BF per acre ((# of 8 ft logs + # of trees)/(2 x # plots)) x 500 Bd ft Example: (((150x2)+30)/(2x5))x500 = 9000 BF/acre or -

Imperial Units
Imperial units From Wikipedia, the free encyclopedia Jump to: navigation, search This article is about the post-1824 measures used in the British Empire and countries in the British sphere of influence. For the units used in England before 1824, see English units. For the system of weight, see Avoirdupois. For United States customary units, see Customary units . Imperial units or the imperial system is a system of units, first defined in the British Weights and Measures Act of 1824, later refined (until 1959) and reduced. The system came into official use across the British Empire. By the late 20th century most nations of the former empire had officially adopted the metric system as their main system of measurement. The former Weights and Measures office in Seven Sisters, London. Contents [hide] • 1 Relation to other systems • 2 Units ○ 2.1 Length ○ 2.2 Area ○ 2.3 Volume 2.3.1 British apothecaries ' volume measures ○ 2.4 Mass • 3 Current use of imperial units ○ 3.1 United Kingdom ○ 3.2 Canada ○ 3.3 Australia ○ 3.4 Republic of Ireland ○ 3.5 Other countries • 4 See also • 5 References • 6 External links [edit] Relation to other systems The imperial system is one of many systems of English or foot-pound-second units, so named because of the base units of length, mass and time. Although most of the units are defined in more than one system, some subsidiary units were used to a much greater extent, or for different purposes, in one area rather than the other. The distinctions between these systems are often not drawn precisely. -

How to Calculate Liquid Application Rates Application Liquid Calculate to How
HOW TO CALCULATE LIQUID APPLICATION RATES Equipment suppliers provide solutions with deluxe control systems, flow meters and GPS speed tracking that can take most guesswork and math out of the liquid application rate equation. But snow professionals should understand the fundamentals used to calculate liquid applications. These cornerstones will help you understand the control data, help you make informed decisions and track how much salt you are putting down and potentially saving. Thirty gallons per acre is a common application rate for pre-treatment and is used in the following equations. Evaluate each account and event and take into account pavement temperature and precipitation. 1 What are you measuring? Determine if you prefer to use gallons per acre or gallons per lane mile. These commonly used measurements are equally effective. 208’ 5,280’ 12’ LANE MILE = 63,360 SQ. FT. ACRE = 208’ 43,560 SQ. FT. • Lane mile is 1.45 times larger than an acre • 30 gallons per acre = 44 gallons per lane mile TEAR OUT AND SAVE TEAR OUT AND SAVE 2 How much salt are you applying? Measuring how much salt or active ingredient is being applied is crucial to understanding salt savings. You can calculate how much less salt you are applying. There is ~2.3 lbs. of salt in a gallon of salt brine at 23.3% salinity. ________lbs. _______ gallons = ____________ 2.3 lbs. of salt x 30 gal. per acre = 69 lbs. of salt per acre HOW TO CALCULATE LIQUID APPLICATION RATES 4 3 Translating your target application rate to gallons per minute Once you know your unit of measurement (i.e., acres vs. -

Your Driving Costs 2020
YOUR DRIVING COSTS 2020 How Much Does it Really Cost to Own a New Car? AAA Average Costs Per Mile Shown to the right are average per-mile costs for 2020 as determined by AAA, based on Miles per Year 10k 15k 20k the driving costs for nine vehicle categories Average Cost 82.36¢ 63.74¢ 54.57¢ weighted by sales. Detailed driving costs in each vehicle category are based on average costs for five top-selling 2020 models selected by AAA and can be found on pages 5 and 6. By category, they are: Î Small Sedan — Honda Civic, Hyundai Elantra, Î Minivan — Chrysler Pacifica, Dodge Grand Nissan Sentra, Toyota Corolla, Volkswagen Jetta Caravan, Kia Sedona, Honda Odyssey, Toyota Sienna Î Medium Sedan — Chevrolet Malibu, Ford Fusion, Honda Accord, Nissan Altima, Toyota Camry Î Pickup Truck — Chevrolet Silverado, Ford F-150, Î Large Sedan — Chevrolet Impala, Chrysler 300, Nissan Titan, Ram 1500 and Toyota Tundra Kia Cadenza, Nissan Maxima, Toyota Avalon Î Hybrid Car — Ford Fusion, Honda Insight, Î Small SUV — Chevrolet Equinox, Ford Escape, Hyundai Ioniq, Toyota Prius Liftback, Toyota Honda CR-V, Nissan Rogue, Toyota RAV4 RAV4 Î Medium SUV — Chevrolet Traverse, Ford Î Electric Car — BMW i3, Chevrolet Bolt, Hyundai Explorer, Honda Pilot, Jeep Grand Cherokee, Kona Electric, Nissan Leaf, Tesla Model 3 Toyota Highlander YOUR DRIVING COSTS | 2020 1 How to Calculate Your Own Driving Costs Start by figuring your gas cost per mile. To do this, you’ll need to keep track of your fueling habits over the course of one year. When your gas tank is full, write down the number of miles on your odometer. -

Estimating Metric and Imperial Linear Conversions
Metric and Imperial Linear Conversions Estimating Metric and Imperial Linear Conversions People estimate distance, time, height and other measurements in everyday life. Estimates are often made using familiar measurements. For example, to measure distance, people may know that 1 step is approximately 1 metre or 1 yard. Using the stride estimate, sizes of rooms, yards and fields can be estimated by walking around them. People often estimate heights of other people based on their own heights. Conversions between metric and imperial units can be estimated using the following guidelines: 1 inch is approximately 3 centimetres 1 yard is approximately 1 metre 1 foot is approximately 0.3 metre 1 mile is approximately 1.5 km. Examples A) A 6-inch pen is approximately 6 × 3 cm = 18 cm. B) A 5-foot sign is approximately 5 × 0.3 = 1.5 metres. C) A distance of 10 yards is approximately 10 metres. D) 60 miles/h is approximately 100 km/h. Calculating Metric and Imperial Linear Conversions It is useful to know how to convert between units in the metric and imperial systems for many reasons, such as when travelling to the United States or following directions to construct something manufactured in the U.S.A. Also, many Canadians refer to height in feet and inches. Imperial measurement is often used in sports, e.g., the yardage in football, lines on a basketball court, 1 mile horse 4 race. Knowledge and Employability Studio Shape and Space: Measurement: Mathematics Linear Measurement: ©Alberta Education, Alberta, Canada (www.LearnAlberta.ca) Metric and Imperial Linear Conversions 1/4 Common conversions between the metric and imperial systems of linear measurement are shown below. -

The International System of Units (SI) - Conversion Factors For
NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v -

The Per-Mile Costs of Operating Compressed Natural Gas Trucks
The per-mile Costs of Operating Compressed Natural Gas Trucks Experience from 16 Million Miles with the Cummins ISX 12G ampCNG AUGUST, 2015 The per-mile Costs of Operating Compressed Natural Gas Trucks Experience from 16 Million Miles with the Cummins ISX12G STEVE JOSEPHS, P.E. OPERATIONS AND ENGINEERING TEAM: LARRY KRISTOFF OBI OFOEGBU CHAD SCHLAEPFER KUSH THAKKAR GRANT ZIMMERMAN Executive Summary This report updates the findings of our earlier report “The Per-Mile Operating Costs of Operating Compressed Natural Gas Trucks and Diesel Trucks”, as of January 31, 2013, by Larry D. Kristoff of Renewable Dairy Fuels, LLC. That report detailed Renewable Dairy Fuels’ experience on prior fleet of 42 heavy duty Kenworth trucks powered by the Cummins 8.9 liter ISL G natural gas engine and compared it with three diesel fleets, one running similar miles per year, a fleet with similar sized engines and one hauling similar loads. We do not attempt to recreate the analysis of operating costs for diesel trucks, but rather document the experience of 16 million miles operating similar Kenworth chassis with the Cummins ISX 12G. As a reminder, the key findings of the previous paper included total maintenance costs for the CNG fleet of $0.122/mile versus a pre-2010 diesel fleet cost of $0.072/mile while fuel economy for the CNG fleet averaged 5.28 miles per diesel gallon equivalent vs. an estimated industry average of 6.1 miles per gallon for diesel fleets. In this report we demonstrate that maintenance costs per mile decreased by 33% in the new generation truck to $0.082/mile, and fuel economy improved 18% to 6.22 miles per gallon. -

Handout – Unit Conversions (Dimensional Analysis)
1 Handout – Unit Conversions (Dimensional Analysis) The Metric System had its beginnings back in 1670 by a mathematician called Gabriel Mouton. The modern version, (since 1960) is correctly called "International System of Units" or "SI" (from the French "Système International"). The metric system has been officially sanctioned for use in the United States since 1866, but it remains the only industrialized country that has not adopted the metric system as its official system of measurement. Many sources also cite Liberia and Burma as the only other countries not to have done so. This section will cover conversions (1) selected units Basic metric units in the metric and American systems, (2) compound or derived measures, and (3) between metric and length meter (m) American systems. Also, (4) applications using conversions will be presented. mass gram (g) The metric system is based on a set of basic units and volume liter (L) prefixes representing powers of 10. time second (s) temperature Celsius (°C) or Kelvin (°K) where C=K-273.15 Prefixes (The units that are in bold are the ones that are most commonly used.) prefix symbol value giga G 1,000,000,000 = 109 ( a billion) mega M 1,000,000 = 106 ( a million) kilo k 1,000 = 103 hecto h 100 = 102 deca da 10 1 1 -1 deci d = 0.1 = 10 10 1 -2 centi c = 0.01 = 10 100 1 -3 milli m = 0.001 = 10 (a thousandth) 1,000 1 -6 micro μ (the Greek letter mu) = 0.000001 = 10 (a millionth) 1,000,000 1 -9 nano n = 0.000000001 = 10 (a billionth) 1,000,000,000 2 To get a sense of the size of the basic units of meter, gram and liter consider the following examples. -
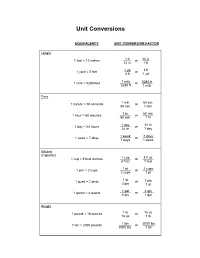
Unit Conversions
Unit Conversions EQUIVALENCY UNIT CONVERSION FACTOR Length 1 foot = 12 inches ____1 ft or ____12 in 12 in 1 ft 1 yd ____3 ft 1 yard = 3 feet ____ or 3 ft 1 yd 1 mile = 5280 feet ______1 mile or ______5280 ft 5280 ft 1 mile Time 1 min 60 sec 1 minute = 60 seconds ______ or ______ 60 sec 1 min 1 hr 60 min 1 hour = 60 minutes ______ or ______ 60 min 1 hr 1 day 24 hr 1 day = 24 hours ______ or ______ 24 hr 1 day ______1 week ______7 days 1 week = 7 days or 7 days 1 week Volume (Capacity) 1 cup = 8 fluid ounces ______1 cup or ______8 fl oz 8 fl oz 1 cup 1 pt 2 cups 1 pint = 2 cups ______ or ______ 2 cups 1 pt ______1 qt 1 quart = 2 pints or ______2 pts 2 pts 1 qt ______1 gal ______4 qts 1 gallon = 4 quarts or 4 qts 1 gal Weight 1 pound = 16 ounces ______1 lb or ______16 oz 16 oz 1 lb 1 ton 2000 lbs 1 ton = 2000 pounds _______ or _______ 2000 lbs 1 ton How to Make a Unit Conversion STEP1: Select a unit conversion factor. Which unit conversion factor we use depends on the units we start with and the units we want to end up with. units we want Numerator Unit conversion factor: units to eliminate Denominator For example, if we want to convert minutes into seconds, we want to eliminate minutes and end up with seconds. Therefore, we would use 60 sec .