Social Welfare Implications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Conditions Générales De Vente Et D'utilisation Du Site
Conditions Générales de Vente et d'Utilisation du site www.oui.sncf CONDITIONS GENERALES DE VENTE ET D'UTILISATION DU SITE WWW.OUI.SNCF ............................................ 1 PREAMBULE ..................................................................................................................................................... 3 CHAPITRE I GENERALITES ........................................................................................................................... 4 ARTICLE 1. DEFINITIONS ET CHAMP D'APPLICATION ...................................................................................... 4 1.1 DEFINITIONS ...................................................................................................................................... 4 1.2 CHAMP D'APPLICATION ..................................................................................................................... 4 ARTICLE 2. UTILISATION DU SITE WWW.OUI.SNCF .............................................................................................. 5 2.1 UTILISER L’ESPACE LOISIR .................................................................................................................. 5 Conditions d’utilisation ................................................................................................................................................ 5 Passation de Commandes ............................................................................................................................................ 6 Annulation -

Rapport Annuel Transport Par Autocar Et Gares Routières 2018
Sommaire SYNTHÈSE 05 03 Les gares routières et AVANT-PROPOS 11 autres aménagements de transport routier 64 AVERTISSEMENT 12 Les aménagements de transport routier 64 Les modalités d’accès aux aménagements 01 de transport routier 68 Les services librement organisés de transport par autocar ANNEXES 77 en 2018 13 Annexe 1 77 La couverture du territoire par les SLO Bilan de l’offre commercialisée par les SLO 13 Bilan de la fréquentation des SLO 26 Annexe 2 78 Caractéristiques des villes desservies par les SLO Résultats économiques et sociaux 31 Les services librement organisés sur des liaisons de Annexe 3 79 100 kilomètres ou moins 34 Les destinations directes au départ des villes desservies Annexe 4 80 02 Part des villes desservies sur les quatre trimestres Annexe 5 81 Analyse de la complémentarité Cartographie des aéroports desservis en 2018 des offres de transport interurbain 50 Annexe 6 82 Substituabilité de l’offre de transport routier Caractéristiques de l’offre de liaisons librement organisé avec des services de transport interurbain conventionnés Annexe 7 83 (routiers, ferroviaires et aériens) 50 Fréquence quotidienne Substituabilité de l’offre de transport routier librement organisé avec des services commerciaux 54 Annexe 8 85 Distance parcourue par les autocars L’offre de transport routier librement organisé sur les liaisons sans alternative modale 57 Annexe 9 86 Comparaison tarifaire des services de transport Caractéristiques de la demande interurbain (routiers, ferroviaires, aériens) 60 Complémentarité de l’offre de transport par -

Edhec Business School, Lille Exchange Report Wong Chin1 Wai, Athena
EXCHANGE REPORT, SPRING 2020 EDHEC BUSINESS SCHOOL, LILLE WONG CHIN WAI, ATHENA INFORMATION SYSTEMS & MARKETING, YEAR 3 TABLE OF CONTENTS Monthly Activity Log………………………………P2-7 General Exchange Information …………………P8-10 Items to Bring ………………………………………P11 Useful Links and Contacts …………………………P11 EDHEC BUSINESS SCHOOL, LILLE EXCHANGE REPORT WONG CHIN1 WAI, ATHENA Monthly Activity Log Late December 2019 Since some friends who went for exchange during Fall, 2019 invited me to go to London for a trip after their exchange and since we will be in Europe at the same time, I decided to ask my other EDHEC Business School exchange friend who would be studying in Nice to book a plane to fly to London first for a short trip with them before reaching France. We took the cheapest flight which requires 2 hours to Singapore, 9 hours stay at Changi Airport and 13 hours to London. Since it was during Christmas period, most restaurants and transports are closed. Fortunately, we found activities for us to do nearby at Hyde Park or within cycling distance. I really enjoyed our time at Winter Wonderland carnival at Hyde Park! After watching the Buckingham Palace march early in the morning, I hopped onto a previously booked London Heathrow Car to catch a flight to Cologne to meet my friend who also ended her Fall semester exchange there. I did not understand how the train ticket system works there at first and was able to enjoy a few free rides. Little did I know how lucky I was for not being caught as Germany is one of the strictest countries concerning fare dodging. -

La Gare Mezzanine De Nantes
OUVERTURE LE 20 LA GARE MEZZANINE NOV. 2020 DE NANTES, UNE ARCHITECTURE REMARQUABLE POUR UNE NOUVELLE GRANDE GARE EN FRANCE AU SERVICE D'UNE MOBILITÉ DURABLE DOSSIER DE PRESSE JEUDI 19 NOV. 2020 G RE DE NANTES CE PROJET EST COFINANCÉ PAR CIRCULONS MIEUX ECHANGEONS PLUS LE FONDS EUROPÉEN DE DÉVELOPPEMENT RÉGIONAL COMMUNIQUÉ DE PRESSE APRÈS TROIS ANS DE TRAVAUX SOUS MAÎTRISES D'OUVRAGE SNCF GARES & CONNEXIONS ET SNCF RÉSEAU, SANS AVOIR JAMAIS INTERROMPU LE TRAFIC FERROVIAIRE, LA NOUVELLE GARE MEZZANINE DE NANTES S’OUVRE AU GRAND PUBLIC VENDREDI 20 NOVEMBRE 2020. Avec près de 17 millions de visiteurs annuels, dont près de 12 millions de voyageurs*, la gare de Nantes se situe à la 6e place des gares les plus fréquentées de France (hors Île-de-France) et à la première de la région des Pays de la Loire. Au cœur d’un territoire dynamique - en termes démographiques et économiques - la gare avait besoin de s’agrandir, de se moderniser, de gagner en confort et en accessibilité pour le plus grand bénéfice des voyageurs et des passants. Ensemble, l’Europe, l’État, la Région des Pays de la Loire, le Département de Loire-Atlantique, Nantes Métropole et le groupe SNCF se sont concertés pour proposer un projet répondant à trois grands enjeux : Un enjeu d’urbanisme Signée de l’architecte international Rudy Ricciotti et construite par le pôle Construction de DEMATHIEU BARD dans le cadre d’un groupement interne réunissant l’agence Infrastructures – Génie Civil Ouest et André BTP, la gare de Nantes s’inscrit dans un vaste projet urbain de transformation de la centralité métropolitaine. -

Long Distance Coach Services in France and Germany: the New European Competition Between Flixbus and Blablabus Laurent Guihéry
Long Distance Coach Services in France and Germany: the new European competition between Flixbus and BlaBlaBus Laurent Guihéry To cite this version: Laurent Guihéry. Long Distance Coach Services in France and Germany: the new European competi- tion between Flixbus and BlaBlaBus. Rivista di Economia e Politica dei Trasporti, Rivista pubblicata dalla Società Italiana di Economia dei Trasporti e della Logistica (SIET) 2019, Numero speciale su ”Il trasporto automobilistico di lunga distanza”, 1 (2019). halshs-02374703 HAL Id: halshs-02374703 https://halshs.archives-ouvertes.fr/halshs-02374703 Submitted on 27 Nov 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Long Distance Coach Services in France and Germany: the new European competition between Flixbus and BlaBlaBus Pagina | 1 Long Distance Coach Services in France and Germany: the new European competition between Flixbus and BlaBlaBus V.2 after referee – 15.09.2019 Laurent Guihéry1* 1 Professor, University of Cergy-Pontoise, MRTE, France Long distance passenger mobility is experiencing a huge structural change in France and Germany. Based on Internet technology and customer-oriented services, new entrants in interurban coach services are diversifying the options for the travelers and have been very successful. -

Etat Des Lieux Régional
SERVICE LOCALISATION ORGANISATEUR AUTRES DONNÉES Départe- MOA / porteur : Exploitant / ges- Public concerné / condi- Date de créa- ID Thématiques Mode Nom du service Description Type de territoire Portée MOA / porteur : nom Sources Commentaires ment type tionnaire tions tion Les MOA ont à 16 Maîtres d'ouvrage : Création : 1995- Près de 1000 km de routes touristiques cyclables aménagées (variantes et antennes charge l'entretien. tous les départements 2013 comprises) de Cuffy (proche de Nevers) à Saint-Brévin-les-Pins (Saint Nazaire). L’itiné- La réalisation : plu- Grand Public (positionne- Ajout 2016 INFRASTRUCTURES 18, 37, et les agglo (compé- Auj : rénovation, VÉLO sieurs organisations 1 ET AMÉNAGEMENTS La Loire à vélo raire traverse les régions Pays de la Loire (373 km) et Centre-Val de Loire (621 km). Tous Régionale CR + CD + CA tence voirie) ment famille qui devient de amélioration http://www.loireavelo.fr/ Mise à jour 2017 41, 45 (syndicats, maîtres Section ouest commune avec l'itinéraire de l’EuroVelo 6, la grande transversale cyclable plus en plus important). avec chacun des Mise à jour 2018 d'ouvrage ou proprié- européenne. Les deux régions grands MOA taires de voirie) Octroi d'une aide financière pour la mise en place de bornes de recharge sur leur terri- Dispositif d’aide visant à toire : Partenariat État- soutenir le déploiement des - SIEIL 37 (Syndicat intercommunal d’énergie d’Indre-et-Loire) 18, 28, Ademe (PIA de 2013 (appel à INFRASTRUCTURES l'État : pro- Syndicats des Syndicats des énergies / Ajout 2016 2 VOITURE infrastructures -
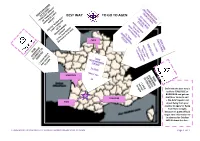
Best Way to Go to Agen
BEST WAY TO GO TO AGEN PARIS BORDEAUX Definitely the best way is to fly to TOULOUSE or BORDEAUX and get our TOULOUSE shuttle or to rent a car ! + We didn’t speak a lot AGEN about flying from your country to Agen/ or flying from Paris to Agen, because it’s quite difficult to get sure information so in advance for October 202120 about this line… GUIDE BOOK TRANSPORTS TO WORLD CHAMPIONSHIP 2021 IN AGEN Page 1 sur 7 HOW TO CONNECT AGEN BY TGV TRAIN PRICES POINT OF DEPARTURE MEANS OF TRANSPORT TIME APPROX. GROUP RESERVATION APPROX. En France • [email protected] DEPENDS ON WHERE IS THE 3H • Phone 0810 879 479 from Monday to friday 8h30 to 18h (0,40 €/minute) FROM SWISS TO “LYON SPECIAL TRAIN TO PARIS DEPARTURE TO • Groups 10 to 30 passengers : www.voyages-train-groupes.sncf.fr STATION” IN PARIS LYRYA AND HOW LONG IN AVANCE 4H 30€/70€/150€ • From SWISS Les gares CFF • https://agents-switzerland.mytraintravel.com • Groups 10 to 30 passengers www.voyages-train-groupes.sncf.fr CONNECTION FROM “LYON STATION” TO “MONTPARNASSE BY SUBWAY ≈22 minutes 1, 90€ By ticket in station or in subway STATION” IN PARIS • Paris – Bruxelles : from 29€ • Paris – Amsterdam : from 35€ • Paris – Cologne : from 35€ • Reservations are opened 4 months in advance for groups. The group offer is not saled DEPENDS ON WHERE IS THE FROM BELGIUM, 2H online. SPECIAL TRAIN TGV DEPARTURE NETHERLANDS, GERMANY TO TO • In France : + 33 8 10 87 94 79, THALYS AND HOW LONG IN AVANCE “NORD STATION” IN PARIS 3H30 30€/70€/150€ • [email protected] • fax au +33 8 10 87 54 75. -

Arafer Bilan Marché Autocars 2019 T2
RÉPUBLIQUE FRANÇAISE Marché librement organisé des services interurbains par autocar Bilan du 2e trimestre 2019 SYNTHESE ................................................................................................................................................ 3 1. BILAN DE L’OFFRE AU DEUXIEME TRIMESTRE 2019 ........................................................................... 4 1.1. Neuf opérateurs sur le marché des SLO dont quatre disposant d’un réseau national ................. 4 1.2. L’offre de dessertes augmente à nouveau ....................................................................................... 4 1.3. Le nombre de liaisons reprend sa croissance .................................................................................. 6 1.4. La concurrence s’effectue toujours sur les liaisons les plus fréquentées tandis que l’offre exclusive progresse .................................................................................................................................... 7 1.5. L’offre s’intensifie moins vite qu’elle ne diversifie ........................................................................... 8 1.6. Les caractéristiques des lignes et des liaisons évoluent peu ......................................................... 8 2. ANALYSE DE LA DEMANDE AU DEUXIEME TRIMESTRE 2019 .............................................................. 9 2.1. La fréquentation au deuxième trimestre 2019 dépasse 2,5 millions de passagers ..................... 9 2.2. La structure de la demande varie lentement .................................................................................. -

Information Package
GUIDE N°1 GRENOBLE CAMPUS BEFORE YOUR ARRIVAL International Students How to prepare you stay in France: First steps Updated on April 2021 Grenoble Ecole de Management Guide N°1 for international students – Grenoble Campus – 2021 – Page 0 Grenoble Ecole de Management Guide N°1 for international students – Grenoble Campus – 2021 – Page 1 WELCOME! To start this new adventure we encourage you to read the following information carefully to know how to prepare your stay as an international student in France. What you will find in this guide? The aim of this guide is to help you understand and prepare the practical side of the adventure you are about to begin. It should answer most of your questions concerning the administrative steps you should organize before your departure and anticipate those you will need to fulfil upon your arrival to settle down in France. These arrangements are under your responsibility, so please take the time to read this guide. We advise you to use only the electronic version as the information is constantly updated. You need further details? You will be contacted with further details to guide you through the preparation phase when your participation into our programs will be confirmed: The International Student Integration Service will schedule a pre-departure campaign for new students from BIB, MIM, MIB, MSc*, MBA and exchange programs. Please note that the French government can make reforms within certain procedures. In case of an important update, future students will be informed by the International Student Integration Service through the pre-departure campaign and during the academic year. -

Parijs-Brussel, Brussel-Parijs Gratis Epub, Ebook
PARIJS-BRUSSEL, BRUSSEL-PARIJS GRATIS Auteur: NB Aantal pagina's: 539 pagina's Verschijningsdatum: none Uitgever: none EAN: 9789061533900 Taal: nl Link: Download hier Bus Parijs Brussel vanaf 5€ Even geduld. Brussel - Parijs. Reistijd 1u Start verkoop vanaf 4 maanden op voorhand. Heen en terug Enkel. Vertrek Aankomst. Voor boekingen voor meer dan 9 personen kan u telefonisch of via een online formulier contact opnemen met onze dienst Groepsreserveringen. Contact Center. Reiziger :. Kinderen jonger dan 4 jaar reizen gratis zonder plaatsreservering. Wilt u een betalende zitplaats voor uw kind, boek deze dan als 'Kind '. Gebruik uw getrouwheidskaart en. Voeg een kaart toe. Wis de lokale opslaggegevens. Hebt u al een My Train account? Meld u aan om nóg sneller te boeken vrijblijvend. Van onderstaande kaarten wordt, indien van toepassing, de korting verrekend op onze website. Met andere kortingskaarten boekt u via het Contact Center. Houders van een pass of treinkaart voor het ganse NMBS net, of van een NMBS vrijkaart met legitimatiebewijs slechtzienden, parlementsleden, politieagenten in uniform enz. Naargelang traject, tijdstip en abonnementsvoorwaarden, reizen houders van een NS-abonnement of OV-chipkaart gratis op het Nederlandse deel van een internationale reis. Ook houders van een pass geldig op het Nederlandse net reizen gratis in Nederland behalve op Thalys. Houders van een pass of treinkaart voor het ganse CFL net, of van een CFL vrijkaart met legitimatiebewijs reizen gratis op het Luxemburgse deel van internationale reizen met klassieke treinen. Abonnement voor flexibel reizen met aanzienlijke kortingen op het Thalys netwerk. Abonnement voor optimaal reizen tussen Brussel en Parijs tegen een vaste prijs. -

Se Déplacer Malin
Partir en vacances – juillet 2020 PRÉSENTATION DE DISPOSITIF SE DEPLACER MALIN POUR LES VACANCES Avion Le Co-voiturage Le covoiturage est le bon moyen pour partager un trajet en voiture, le rendre moins cher et plus convivial. Le covoiturage est adapté pour des déplacements quotidiens ou pour des trajets occasionnels longs ou courts. De nombreux sites existent de mises en relation. En général vous pouvez consulter un barème de prix selon les distances. MOBILI THI http://www.mobilithi.fr/ covoiturage depuis Thionville KARZOO http://www.karzoo.lu/ Portail de covoiturage au Luxembourg MOBICOOP https://www.mobicoop.fr/ BLABLA CAR https://www.blablacar.fr/ Auto-partage L’auto-partage est la mise en commun d’un ou plusieurs véhicule, utilisé(s) pour des trajets différents à des moments différents. Il revêt trois formes : L’auto-partage entre particuliers, le service d’auto-partage géré par des sociétés spécialisés et enfin la location de véhicules entre particuliers. Fonctionnement de l’auto-partage entre particuliers : Les personnes se mettent d’accord sur les règles de fonctionnement, qu’elles inscrivent dans un contrat signé par chacune. Un conducteur réserve le véhicule, il l’utilise, note ses kilomètres et les personnes font les comtes tous les mois ou en fin d’année. CITIZLORRAINE http://lorraine.citiz.coop/ développe une activité d'auto-partage à l'échelle du Sillon Lorrain. GETAROUND https://fr.getaround.com/ location de voiture entre particuliers. Autostop Voyager librement et de façon aventureuse en autostop. Lever le pouce sur le bord de la route et attendre de monter dans un véhicule, partager un moment du trajet avec quelqu’un. -

Urban Mobility Transition Drivers
Project ID: 814910 LC-MG-1-3-2018 - Harnessing and understanding the impacts of changes in urban mobility on policy making by city-led innovation for sustainable urban mobility Sustainable Policy RespOnse to Urban mobility Transition D2.3: Urban Mobility Transition Drivers Work package: WP 2 - Understanding transition in urban mobility Geert te Boveldt, Sara Tori, Imre Keseru, Cathy Macharis Authors: (VUB) City of Almada, City of Arad, BKK Centre for Budapest Transport, City of Gothenburg, City of ‘s Hertogenbosch, City of Ioannina, City of Mechelen, City of Minneapolis, Contributors: City of Padova, City of Tel Aviv, City of Valencia, Region of Ile-de-France, Municipality of Kalisz, West Midlands Combined Authority, Aristos Halatsis (CERTH), Piero Valmassoi (Polis) Status: Final Date: Jan 30, 2020 Version: 1.0 Classification: PU-Public Disclaimer: The SPROUT project is co-funded by the European Commission under the Horizon 2020 Framework Programme. This document reflects only authors’ views. EC is not liable for any use that may be done of the information contained therein. D2.3: Urban Mobility Transition Drivers SPROUT Project Profile Project ID: 814910; H2020- LC-MG-1-3-2018 Acronym: SPROUT Title: Sustainable Policy RespOnse to Urban mobility Transition URL: Start Date: 01/09/2019 Duration: 36 Months 3 D2.3: Urban Mobility Transition Drivers Table of Contents 1 Executive Summary ......................................................................... 10 2 Introduction .....................................................................................