DOCSLIB.ORG

Math 3A Notes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math 3A Notes 5. Orthogonality 5.1. The Scalar Product in Euclidean Space 5.1 The Scalar Product in Rn Thusfar we have restricted ourselves to vector spaces and the operations of addition and scalar multiplication: how else might we combine vectors? You should know about the scalar (dot) and cross products of vectors in R3 The scalar product extends nicely to other vector spaces, while the cross product is another story1 The basic purpose of scalar products is to define and analyze the lengths of and angles between vectors2 1But not for this class! You may see ‘wedge’ products in later classes. 2It is important to note that everything in this chapter, until mentioned, only applies to real vector spaces (where F = R) 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Euclidean Space Definition 5.1.1 Suppose x, y Rn are written with respect to the standard 2 basis e ,..., e f 1 ng 1 The scalar product of x, y is the real numbera (x, y) := xTy = x y + x y + + x y 1 1 2 2 ··· n n 2 x, y are orthogonal or perpendicular if (x, y) = 0 3 n-dimensional Euclidean Space Rn is the vector space of n 1 column vectors R × together with the scalar product aOther notations include x y and x, y · h i Euclidean Space is more than just a collection of co-ordinates vectors: it implicitly comes with notions of angle and length3 Important Fact: (y, x) = yTx = (xTy)T = xTy = (x, y) so the scalar product is symmetric 3To be seen in R2 and R3 shortly 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Angles and Lengths Definition 5.1.2 p The length of a vector x Rn is its norm x = (x, x) 2 jj jj The distance between two vectors x, y is given by y x jj − jj y (y1, y2) Theorem 5.1.3 q [0, p] y x The angle between two vectors − 2 y x, y in R2 or R3 satisfies the equation (x , x ) θ 1 2 (x, y) = x y cos q x jj jj jj jj x Definition 5.1.4 We define the angle q between x, y Rn to be the number 2 1 (x, y) q = cos− x y jj jj jj jj 1 q is the smaller of the two possible angles, since cos− has range [0, p] 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Proof of Theorem. If x, y are parallel then q = 0 or p and the Theorem is trivial Otherwise, in R2 (or in the plane 3 Span(x, y) R ), the cosine rule y ≤ (y1, y2) holds: y x − y x y 2 = x 2 + y 2 2 x y cos q jj − jj jj jj jj jj − jj jj jj jj (x , x ) θ 1 2 Applying the definition of norm and scalar product,x we obtain x 2 x y cos q = x 2 + y 2 x y 2 jj jj jj jj jj jj jj jj − jj − jj = xTx + yTy (x y)T(x y) − − − = xTx + yTy (xTx + yTy xTy yTx) − − − = xTy + yTx = 2(x, y) as required 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Basic results & inequalities Several results that you will have used without thinking in elementary geometry follow directly from the definitions Theorem 5.1.5 (Cauchy–Schwarz inequality) If x, y are vectors in Rn then (x, y) x y j j ≤ jj jj jj jj with equality iff x, y are parallel Proof. (x, y) = x y cos q = x y cos q x y j j jj jj jj jj jj jj jj jj j j ≤ jj jj jj jj Equality is satisfied precisely when cos q = 1: that is when ± q = 0, p, and so x, y are parallel 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Theorem 5.1.6 (Triangle inequality) If x, y Rn then x + y x + y 2 jj jj ≤ jj jj jj jj I.e. Any side of a triangle is shorter than the sum of the others y Proof. x + y 2 = (x + y, x + y) = (x + y)T(x + y) jj jj 2 2 = x + 2(x, y) + y y jj jj jj jj 2 2 x + 2 (x, y) + y x + y ≤ jj jj j j jj jj x 2 + 2 x y + y 2 ≤ jj jj jj jj jj jj jj jj 2 = ( x + y ) x jj jj jj jj x If (x, y) = 0, the second line in the proof of the triangle inequality immediately yields Theorem 5.1.7 (Pythagoras’) If x, y Rn are orthogonal then x + y 2 = x 2 + y 2 2 jj jj jj jj jj jj 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Example 1 3 Let x = 2 and y = −1 , then 1 3 − q x = (x, x) = p1 + 4 + 1 = p6 jj jj y = p9 + 1 + 9 = p19 jj jj (x, y) = 3 + 2 3 = 4 − − − 1 (x, y) 1 4 q = cos− = cos− − x y p6p19 jj jj jj jj 1.955 rad 112◦ ≈ ≈ 4 y x = −1 = p33 jj − jj −4 p6 + p19 ≤ 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Projections Scalar products are useful for calculating how much of one vector points in the direction of another Definition 5.1.8 Rn 1 The unit vector in the direction of v is the vector v v 2 jj jj The scalar projection of x onto v = 0 in Rn is 6 the scalar product 1 (v, x) a (x) = v, x = v v v jj jj jj jj x The orthogonal (or vector) projection of x onto v = 0 in Rn is 6 1 (v, x) v pv(x) = av(x) v = 2 v v v πv(x) jj jj jj jj Note: a (x) = p (x) : if a (x) < 0 then the projection of x v 6 jj v jj v onto v points in the opposite direction to v 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Orthogonal projection means several things: 1 p (Rn) (p is a linear map) v 2 L v n 2 pv(R ) = Span(v) (Projection onto Span(v)) 3 pv(v) = v (Identity on Span(v)) 4 ker p = v = y Rn : (y, v) = 0 (Orthogonality) v ? f 2 g 1 , 2 , 3 say that pv is a projection 4 makes the projection orthogonal: any- x thing orthogonal to v is mapped to zero ker πv n v Similarly av (R , R) 2 L πv(x) 5. Orthogonality 5.1. The Scalar Product in Euclidean Space The matrix of a projection Since pv is a linear map, it has a standard matrix representation Indeed (v, x) (v, x) vTx vvT pv(x) = v = v = v = x v 2 v 2 v 2 v 2 jj jj jj jj jj jj jj jj vvT whence the matrix of pv is the n n matrix 2 v × jj jj Example 2 x In R , orthogonal projection onto v = ( y ) has matrix 1 x 1 x2 xy A = (x y) = v x2 + y2 y x2 + y2 xy y2 1 0 Projection onto the x-axis is therefore Ai = 0 0 , while 1 1 1 projection onto the line y = x is Ai+j = 2 1 1 5. Orthogonality 5.1. The Scalar Product in Euclidean Space Planes in R3 Projections are useful for describing planes4 in R3 a Let P be the plane normal to n = b R3 and which passes c 2 x0 through the point with position vector x0 = y0 z0 The distance d of the plane from the origin is the scalar projection of any vector in the plane onto n: thus (x , n) d = a (x ) = 0 n 0 n jj jj ax + by + cz = 0 0 0 pa2 + b2 + c2 4And more general affine spaces in arbitrary dimension 5. Orthogonality 5.1. The Scalar Product in Euclidean Space The plane P is the set of points whose scalar projection onto n is d: otherwise said P = x : a (x) = d = a (x ) f n n 0 g However a (x) = a (x ) a (x x ) = 0 (x x , n) = 0 n n 0 () n − 0 () − 0 a(x x ) + b(y y ) + c(z z ) = 0 () − 0 − 0 − 0 which is an alternative description of the plane Example 7 0 If x0 = 9 , and n = 3 , then P has equation 3 1 3(y 9) + (z 3) = 0 or 3y + z = 30 − − The distance to P is (x0, n) 30 d = an(x0) = = n p10 jj jj 5. Orthogonality 5.1. The Scalar Product in Euclidean Space The distance of a vector y from P is the scalar projection of y onto the normal n with d subtracted: dist(y, P) = a (y) d n − (n, y) = a (x ) n − n 0 jj jj (n, y x ) = − 0 n jj jj Example 3 7 0 If y = 2 , x0 = 9 , and n = 3 , then 1 3 1 23 dist(y, P) = − p10 The negative sign means that y is ‘below’ P (on the opposite side of P to the direction of n) 5. Orthogonality 5.2. Orthogonal subspaces 5.2 Orthogonal subspaces Recall that x, y Rn are orthogonal if (x, y) = xTy = 0 2 Definition 5.2.1 Two subspaces U, V Rn are orthogonal, written U V, iff ≤ ? (u, v) = 0 for all u U, v V 2 2 The orthogonal complement to U in Rn is the subspace n U? := x R : (x, u) = 0, u U f 2 8 2 g E.g.
Load more

Recommended publications
  • Linear Algebra for Dummies
    Linear Algebra for Dummies Jorge A. Menendez October 6, 2017 Contents 1 Matrices and Vectors1 2 Matrix Multiplication2 3 Matrix Inverse, Pseudo-inverse4 4 Outer products 5 5 Inner Products 5 6 Example: Linear Regression7 7 Eigenstuff 8 8 Example: Covariance Matrices 11 9 Example: PCA 12 10 Useful resources 12 1 Matrices and Vectors An m × n matrix is simply an array of numbers: 2 3 a11 a12 : : : a1n 6 a21 a22 : : : a2n 7 A = 6 7 6 . 7 4 . 5 am1 am2 : : : amn where we define the indexing Aij = aij to designate the component in the ith row and jth column of A. The transpose of a matrix is obtained by flipping the rows with the columns: 2 3 a11 a21 : : : an1 6 a12 a22 : : : an2 7 AT = 6 7 6 . 7 4 . 5 a1m a2m : : : anm T which evidently is now an n × m matrix, with components Aij = Aji = aji. In other words, the transpose is obtained by simply flipping the row and column indeces. One particularly important matrix is called the identity matrix, which is composed of 1’s on the diagonal and 0’s everywhere else: 21 0 ::: 03 60 1 ::: 07 6 7 6. .. .7 4. .5 0 0 ::: 1 1 It is called the identity matrix because the product of any matrix with the identity matrix is identical to itself: AI = A In other words, I is the equivalent of the number 1 for matrices. For our purposes, a vector can simply be thought of as a matrix with one column1: 2 3 a1 6a2 7 a = 6 7 6 .
    [Show full text]
  • Eigenvalues and Eigenvectors
    Jim Lambers MAT 605 Fall Semester 2015-16 Lecture 14 and 15 Notes These notes correspond to Sections 4.4 and 4.5 in the text. Eigenvalues and Eigenvectors In order to compute the matrix exponential eAt for a given matrix A, it is helpful to know the eigenvalues and eigenvectors of A. Definitions and Properties Let A be an n × n matrix. A nonzero vector x is called an eigenvector of A if there exists a scalar λ such that Ax = λx: The scalar λ is called an eigenvalue of A, and we say that x is an eigenvector of A corresponding to λ. We see that an eigenvector of A is a vector for which matrix-vector multiplication with A is equivalent to scalar multiplication by λ. Because x is nonzero, it follows that if x is an eigenvector of A, then the matrix A − λI is singular, where λ is the corresponding eigenvalue. Therefore, λ satisfies the equation det(A − λI) = 0: The expression det(A−λI) is a polynomial of degree n in λ, and therefore is called the characteristic polynomial of A (eigenvalues are sometimes called characteristic values). It follows from the fact that the eigenvalues of A are the roots of the characteristic polynomial that A has n eigenvalues, which can repeat, and can also be complex, even if A is real. However, if A is real, any complex eigenvalues must occur in complex-conjugate pairs. The set of eigenvalues of A is called the spectrum of A, and denoted by λ(A). This terminology explains why the magnitude of the largest eigenvalues is called the spectral radius of A.
    [Show full text]
  • Algebra of Linear Transformations and Matrices Math 130 Linear Algebra
    Then the two compositions are 0 −1 1 0 0 1 BA = = 1 0 0 −1 1 0 Algebra of linear transformations and 1 0 0 −1 0 −1 AB = = matrices 0 −1 1 0 −1 0 Math 130 Linear Algebra D Joyce, Fall 2013 The products aren't the same. You can perform these on physical objects. Take We've looked at the operations of addition and a book. First rotate it 90◦ then flip it over. Start scalar multiplication on linear transformations and again but flip first then rotate 90◦. The book ends used them to define addition and scalar multipli- up in different orientations. cation on matrices. For a given basis β on V and another basis γ on W , we have an isomorphism Matrix multiplication is associative. Al- γ ' φβ : Hom(V; W ) ! Mm×n of vector spaces which though it's not commutative, it is associative. assigns to a linear transformation T : V ! W its That's because it corresponds to composition of γ standard matrix [T ]β. functions, and that's associative. Given any three We also have matrix multiplication which corre- functions f, g, and h, we'll show (f ◦ g) ◦ h = sponds to composition of linear transformations. If f ◦ (g ◦ h) by showing the two sides have the same A is the standard matrix for a transformation S, values for all x. and B is the standard matrix for a transformation T , then we defined multiplication of matrices so ((f ◦ g) ◦ h)(x) = (f ◦ g)(h(x)) = f(g(h(x))) that the product AB is be the standard matrix for S ◦ T .
    [Show full text]
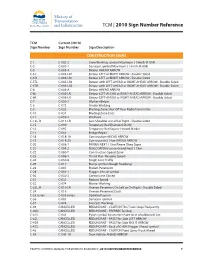
  • 2010 Sign Number Reference for Traffic Control Manual
    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
    [Show full text]
  • Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes
    Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes April 24, 2018 James Smith [email protected] https://mx.linkedin.com/in/james-smith-1b195047 \Our first step in developing an expression for the orientation of \our" gnomon: Diagramming its location at the instant of the 2016 December solstice." Abstract Because the shortage of worked-out examples at introductory levels is an obstacle to widespread adoption of Geometric Algebra (GA), we use GA to calculate Solar azimuths and altitudes as a function of time via the heliocentric model. We begin by representing the Earth's motions in GA terms. Our representation incorporates an estimate of the time at which the Earth would have reached perihelion in 2017 if not affected by the Moon's gravity. Using the geometry of the December 2016 solstice as a starting 1 point, we then employ GA's capacities for handling rotations to determine the orientation of a gnomon at any given latitude and longitude during the period between the December solstices of 2016 and 2017. Subsequently, we derive equations for two angles: that between the Sun's rays and the gnomon's shaft, and that between the gnomon's shadow and the direction \north" as traced on the ground at the gnomon's location. To validate our equations, we convert those angles to Solar azimuths and altitudes for comparison with simulations made by the program Stellarium. As further validation, we analyze our equations algebraically to predict (for example) the precise timings and locations of sunrises, sunsets, and Solar zeniths on the solstices and equinoxes.
    [Show full text]
  • Schaum's Outline of Linear Algebra (4Th Edition)
    SCHAUM’S SCHAUM’S outlines outlines Linear Algebra Fourth Edition Seymour Lipschutz, Ph.D. Temple University Marc Lars Lipson, Ph.D. University of Virginia Schaum’s Outline Series New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto Copyright © 2009, 2001, 1991, 1968 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior writ- ten permission of the publisher. ISBN: 978-0-07-154353-8 MHID: 0-07-154353-8 The material in this eBook also appears in the print version of this title: ISBN: 978-0-07-154352-1, MHID: 0-07-154352-X. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. To contact a representative please e-mail us at [email protected]. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (“McGraw-Hill”) and its licensors reserve all rights in and to the work.
    [Show full text]
  • Equations of Lines and Planes
    Equations of Lines and 12.5 Planes Copyright © Cengage Learning. All rights reserved. Lines A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given. The equation of the line can then be written using the point-slope form. Likewise, a line L in three-dimensional space is determined when we know a point P0(x0, y0, z0) on L and the direction of L. In three dimensions the direction of a line is conveniently described by a vector, so we let v be a vector parallel to L. 2 Lines Let P(x, y, z) be an arbitrary point on L and let r0 and r be the position vectors of P0 and P (that is, they have representations and ). If a is the vector with representation as in Figure 1, then the Triangle Law for vector addition gives r = r0 + a. Figure 1 3 Lines But, since a and v are parallel vectors, there is a scalar t such that a = t v. Thus which is a vector equation of L. Each value of the parameter t gives the position vector r of a point on L. In other words, as t varies, the line is traced out by the tip of the vector r. 4 Lines As Figure 2 indicates, positive values of t correspond to points on L that lie on one side of P0, whereas negative values of t correspond to points that lie on the other side of P0.
    [Show full text]
  • Math 217: Multilinearity of Determinants Professor Karen Smith (C)2015 UM Math Dept Licensed Under a Creative Commons By-NC-SA 4.0 International License
    Math 217: Multilinearity of Determinants Professor Karen Smith (c)2015 UM Math Dept licensed under a Creative Commons By-NC-SA 4.0 International License. A. Let V −!T V be a linear transformation where V has dimension n. 1. What is meant by the determinant of T ? Why is this well-defined? Solution note: The determinant of T is the determinant of the B-matrix of T , for any basis B of V . Since all B-matrices of T are similar, and similar matrices have the same determinant, this is well-defined—it doesn't depend on which basis we pick. 2. Define the rank of T . Solution note: The rank of T is the dimension of the image. 3. Explain why T is an isomorphism if and only if det T is not zero. Solution note: T is an isomorphism if and only if [T ]B is invertible (for any choice of basis B), which happens if and only if det T 6= 0. 3 4. Now let V = R and let T be rotation around the axis L (a line through the origin) by an 21 0 0 3 3 angle θ. Find a basis for R in which the matrix of ρ is 40 cosθ −sinθ5 : Use this to 0 sinθ cosθ compute the determinant of T . Is T othogonal? Solution note: Let v be any vector spanning L and let u1; u2 be an orthonormal basis ? for V = L . Rotation fixes ~v, which means the B-matrix in the basis (v; u1; u2) has 213 first column 405.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • Lecture 3.Pdf
    ENGR-1100 Introduction to Engineering Analysis Lecture 3 POSITION VECTORS & FORCE VECTORS Today’s Objectives: Students will be able to : a) Represent a position vector in Cartesian coordinate form, from given geometry. In-Class Activities: • Applications / b) Represent a force vector directed along Relevance a line. • Write Position Vectors • Write a Force Vector along a line 1 DOT PRODUCT Today’s Objective: Students will be able to use the vector dot product to: a) determine an angle between In-Class Activities: two vectors, and, •Applications / Relevance b) determine the projection of a vector • Dot product - Definition along a specified line. • Angle Determination • Determining the Projection APPLICATIONS This ship’s mooring line, connected to the bow, can be represented as a Cartesian vector. What are the forces in the mooring line and how do we find their directions? Why would we want to know these things? 2 APPLICATIONS (continued) This awning is held up by three chains. What are the forces in the chains and how do we find their directions? Why would we want to know these things? POSITION VECTOR A position vector is defined as a fixed vector that locates a point in space relative to another point. Consider two points, A and B, in 3-D space. Let their coordinates be (XA, YA, ZA) and (XB, YB, ZB), respectively. 3 POSITION VECTOR The position vector directed from A to B, rAB , is defined as rAB = {( XB –XA ) i + ( YB –YA ) j + ( ZB –ZA ) k }m Please note that B is the ending point and A is the starting point.
    [Show full text]
  • Basic Multivector Calculus, Proceedings of FAN 2008, Hiroshima, Japan, 23+24 October 2008
    E. Hitzer, Basic Multivector Calculus, Proceedings of FAN 2008, Hiroshima, Japan, 23+24 October 2008. Basic Multivector Calculus Eckhard Hitzer, Department of Applied Physics, Faculty of Engineering, University of Fukui Abstract: We begin with introducing the generalization of real, complex, and quaternion numbers to hypercomplex numbers, also known as Clifford numbers, or multivectors of geometric algebra. Multivectors encode everything from vectors, rotations, scaling transformations, improper transformations (reflections, inversions), geometric objects (like lines and spheres), spinors, and tensors, and the like. Multivector calculus allows to define functions mapping multivectors to multivectors, differentiation, integration, function norms, multivector Fourier transformations and wavelet transformations, filtering, windowing, etc. We give a basic introduction into this general mathematical language, which has fascinating applications in physics, engineering, and computer science. more didactic approach for newcomers to geometric algebra. 1. Introduction G(I) is the full geometric algebra over all vectors in the “Now faith is being sure of what we hope for and certain of what we do not see. This is what the ancients were n-dimensional unit pseudoscalar I e1 e2 ... en . commended for. By faith we understand that the universe was formed at God’s command, so that what is seen was not made 1 A G (I) is the n-dimensional vector sub-space of out of what was visible.” [7] n The German 19th century mathematician H. Grassmann had grade-1 elements in G(I) spanned by e1,e2 ,...,en . For the clear vision, that his “extension theory (now developed to geometric calculus) … forms the keystone of the entire 1 vectors a,b,c An G (I) and scalars , ,, ; structure of mathematics.”[6] The algebraic “grammar” of this universal form of calculus is geometric algebra (or Clifford G(I) has the fundamental properties of algebra).
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]