DOCSLIB.ORG

A Tutorial on Euler Angles and Quaternions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

A Tutorial on Euler Angles and Quaternions Moti Ben-Ari Department of Science Teaching Weizmann Institute of Science http://www.weizmann.ac.il/sci-tea/benari/ Version 2.0.1 c 2014–17 by Moti Ben-Ari. This work is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/ by-sa/3.0/ or send a letter to Creative Commons, 444 Castro Street, Suite 900, Mountain View, California, 94041, USA. Chapter 1 Introduction You sitting in an airplane at night, watching a movie displayed on the screen attached to the seat in front of you. The airplane gently banks to the left. You may feel the slight acceleration, but you won’t see any change in the position of the movie screen. Both you and the screen are in the same frame of reference, so unless you stand up or make another move, the position and orientation of the screen relative to your position and orientation won’t change. The same is not true with respect to your position and orientation relative to the frame of reference of the earth. The airplane is moving forward at a very high speed and the bank changes your orientation with respect to the earth. The transformation of coordinates (position and orientation) from one frame of reference is a fundamental operation in several areas: flight control of aircraft and rockets, move- ment of manipulators in robotics, and computer graphics. This tutorial introduces the mathematics of rotations using two formalisms: (1) Euler angles are the angles of rotation of a three-dimensional coordinate frame. A rotation of Euler angles is represented as a matrix of trigonometric functions of the angles. (2) Quaternions are an algebraic structure that extends the familiar concept of complex numbers. While quaternions are much less intuitive than angles, rotations defined by quaternions can be computed more efficiently and with more stability, and therefore are widely used. The tutorial assumes an elementary knowledge of trigonometry and matrices. The compu- tations will be given in great detail for two reasons. First, so that you can be convinced of the correctness of the formulas, and, second, so that you can learn how to do them yourselves, in case you come across a context that uses different definitions or notation. For a comprehensive presentation of quaternions using vector algebra, see: John Vince. Quaternions for Computer Graphics, 2011, Springer. 1 Chapter 2 Rotations in two dimensions We start by discussing rotations in two dimensions; the concepts and formulas should be familiar and a review will facilitate learning about rotations in three dimensions. 2.1 Cartesian and polar coordinates A vector or a position (the tip of the vector) in a two-dimensional space can be given either in cartesian coordinates (x, y) or in polar coordinates (r, f), relative to a frame of reference: x r y φ The formulas for transforming one representation to another are: x = r cos f y = r sin f q r = x2 + y2 1 y f = tan− . x 2.2 Rotating a vector Suppose now that the vector is rotated by the angle q: x0 y0 r x r y θ φ 2 The new vector’s polar coordinates are (r, f + q) and its cartesian coordinates can be computed using the trigonometric identities for the sum of two angles: x0 = r cos(f + q) = r(cos f cos q sin f sin q) − = (r cos f) cos q (r sin f) sin q − = x cos q y sin q, − y0 = r sin(f + q) = r(sin f cos q + cos f sin q) = (r sin f) cos q + (r cos f) sin q = y cos q + x sin q = x sin q + y cos q . The transformation of the position (x, y) to (x0, y0) caused by a rotation through the angle q can be expressed in matrix notation as: " # " #" # x cos q sin q x 0 = − . y0 sin q cos q y Example Let r = 1 and let both q and f be 30◦ so that: x = r cos f = cos f = cos q = cos 30◦ = p3/2 y = r sin f = sin f = sin q = sin 30◦ = 1/2 . We can now compute the values of x0 and y0: " # " #" # " # " # x p3/2 1/2 p3/2 (p3/2)2 (1/2)2 1/2 0 = − = − = . y 1/2 p3/2 1/2 1/2 p3/2 + 1/2 p3/2 p3/2 0 · · The result makes sense since f + q = 60◦. 2.3 A geometric derivation of the rotation matrix The rotation matrix can be derived geometrically. Rather than look at the vector, let us look at its x and y components and rotate them (counterclockwise) by q (Figure 2.1). The x- and y- components are rotated by the angle q so that the OAB becomes OA0B0. Construct two right triangles: (1) Drop the perpendicular from A0 to the x-axis to form the right triangle OA C; (b) Construct a line through A parallel to the x-axis and a line 4 0 0 through B parallel to the y-axis. They intersect at C to form the right triangle B A C . 0 0 4 0 0 0 Since A C is parallel to CO, C A O = A OC = q. OA B is a right angle and A B C 0 0 6 0 0 6 0 6 0 0 4 0 0 0 is a right triangle so 6 A0B0C0 = q. The sides of the two right triangles are labeled with 3 B0 = (x0, y0) θ y cos θ y B = (x, y) 90 θ C − A 0 y sin θ 0 sin θ x x θ O A x cos θ C Figure 2.1: Geometric derivation of the rotation matrix their lengths obtained by trigonometry. It is now easy to see that x0 is the length of OC minus the length of A0C0 and that y0 is the length of CA0 plus the length of C0B0: x0 = x cos q y sin q − y0 = x sin q + y cos q. 2.4 Rotating the frame of reference The effect of rotating a vector by q is the same as the effect obtained by rotation of the frame of reference. The left diagram below shows a vector in the frame of reference A. The right diagram shows the same vector after frame A is rotated q relative to a new frame B. (xA, yA), (xB, yB) yA (xA, yA) yB yA r xA r φ φ xA θ xB Given the coordinates (xA, yA) of the points in the frame A: xA = r cos f yA = r sin f, 4 what are its coordinates (xB, yB) in the frame B? The geometry of this diagram is the same as the geometry of the diagram in Section 2.2, so we can use the same equation: " # " #" # x cos q sin q x B = − A . (2.1) yB sin q cos q yA Example Consider the point (xA, yA) = (p3/2, 1/2) in frame A. What are the coordinates of the point in frame B? As before, the computation gives: " # " #" # " # x p3/2 1/2 p3/2 1/2 B = − = . yB 1/2 p3/2 1/2 p3/2 2.5 Multiple rotations Rotate the coordinate frame B by y relative to a new frame C. (xA, yA), (xB, yB), (xC, yC) xA yC yB r xB yA φ θ ψ xC If we know (xB, yB), we can multiply it by the rotation matrix for y to obtain (xC, yC). B Let us denote the rotation matrix from frame A to frame B by RA and the rotation matrix C A from frame B to frame C by RB. Given p , the coordinates of a point in frame A, its B B A C C C B coordinates in frame B are p = RA p , and p , its coordinates in frame C, are p = RB p . Combining the two equations we have: C C B C B A p = RB p = RB RA p . C C B Let RA = RB RA. This is the rotation matrix from A to C, so we can obtain the coordinates pC directly from pA by: C C A p = RA p . Example C B Let y = 30◦ so RB = RA. Then: " # " #" # " # x p3/2 1/2 1/2 0 C = − = . yC 1/2 p3/2 p3/2 1 5 From the drawing we see the vector lies on the yC-axis which corresponds to the coordi- nates (0, 1). Let us now compute: " p #" p # " p # C C B 3/2 1/2 3/2 1/2 1/2 3/2 RA = RB RA = − − = − . 1/2 p3/2 1/2 p3/2 p3/2 1/2 C C A The computation p = RA p is: " # " #" # " # x 1/2 p3/2 p3/2 0 C = − = , yC p3/2 1/2 1/2 1 the same result obtained in the two-stage computation. Example Consider the vector (1, 0) lying on the x-axis of frame A. Rotate A by 15◦ to frame B and then rotate frame B by 30◦ to frame C. Hopefully, the coordinates of the vector in frame C will be (p2/2, p2/2), because the vector makes an angle of 45◦ with the x-axis of frame C. The values of the trigonometric functions for 15◦ are: p6 + p2 p6 p2 cos 15◦ = , sin 15◦ − . 4 4 First rotate by 15◦: " # " p6+p2 p6 p2 #" # " p6+p2 # xB − 1 = 4 − 4 = 4 .
Recommended publications
  • Quaternions and Cli Ord Geometric Algebras

    Quaternions and Cli Ord Geometric Algebras

    Quaternions and Cliord Geometric Algebras Robert Benjamin Easter First Draft Edition (v1) (c) copyright 2015, Robert Benjamin Easter, all rights reserved. Preface As a rst rough draft that has been put together very quickly, this book is likely to contain errata and disorganization. The references list and inline citations are very incompete, so the reader should search around for more references. I do not claim to be the inventor of any of the mathematics found here. However, some parts of this book may be considered new in some sense and were in small parts my own original research. Much of the contents was originally written by me as contributions to a web encyclopedia project just for fun, but for various reasons was inappropriate in an encyclopedic volume. I did not originally intend to write this book. This is not a dissertation, nor did its development receive any funding or proper peer review. I oer this free book to the public, such as it is, in the hope it could be helpful to an interested reader. June 19, 2015 - Robert B. Easter. (v1) [email protected] 3 Table of contents Preface . 3 List of gures . 9 1 Quaternion Algebra . 11 1.1 The Quaternion Formula . 11 1.2 The Scalar and Vector Parts . 15 1.3 The Quaternion Product . 16 1.4 The Dot Product . 16 1.5 The Cross Product . 17 1.6 Conjugates . 18 1.7 Tensor or Magnitude . 20 1.8 Versors . 20 1.9 Biradials . 22 1.10 Quaternion Identities . 23 1.11 The Biradial b/a .
  • Understanding Euler Angles 1

    Understanding Euler Angles 1

    Welcome Guest View Cart (0 items) Login Home Products Support News About Us Understanding Euler Angles 1. Introduction Attitude and Heading Sensors from CH Robotics can provide orientation information using both Euler Angles and Quaternions. Compared to quaternions, Euler Angles are simple and intuitive and they lend themselves well to simple analysis and control. On the other hand, Euler Angles are limited by a phenomenon called "Gimbal Lock," which we will investigate in more detail later. In applications where the sensor will never operate near pitch angles of +/‐ 90 degrees, Euler Angles are a good choice. Sensors from CH Robotics that can provide Euler Angle outputs include the GP9 GPS‐Aided AHRS, and the UM7 Orientation Sensor. Figure 1 ‐ The Inertial Frame Euler angles provide a way to represent the 3D orientation of an object using a combination of three rotations about different axes. For convenience, we use multiple coordinate frames to describe the orientation of the sensor, including the "inertial frame," the "vehicle‐1 frame," the "vehicle‐2 frame," and the "body frame." The inertial frame axes are Earth‐fixed, and the body frame axes are aligned with the sensor. The vehicle‐1 and vehicle‐2 are intermediary frames used for convenience when illustrating the sequence of operations that take us from the inertial frame to the body frame of the sensor. It may seem unnecessarily complicated to use four different coordinate frames to describe the orientation of the sensor, but the motivation for doing so will become clear as we proceed. For clarity, this application note assumes that the sensor is mounted to an aircraft.
  • Arxiv:1001.0240V1 [Math.RA]

    Arxiv:1001.0240V1 [Math.RA]

    Fundamental representations and algebraic properties of biquaternions or complexified quaternions Stephen J. Sangwine∗ School of Computer Science and Electronic Engineering, University of Essex, Wivenhoe Park, Colchester, CO4 3SQ, United Kingdom. Email: [email protected] Todd A. Ell† 5620 Oak View Court, Savage, MN 55378-4695, USA. Email: [email protected] Nicolas Le Bihan GIPSA-Lab D´epartement Images et Signal 961 Rue de la Houille Blanche, Domaine Universitaire BP 46, 38402 Saint Martin d’H`eres cedex, France. Email: [email protected] October 22, 2018 Abstract The fundamental properties of biquaternions (complexified quaternions) are presented including several different representations, some of them new, and definitions of fundamental operations such as the scalar and vector parts, conjugates, semi-norms, polar forms, and inner and outer products. The notation is consistent throughout, even between representations, providing a clear account of the many ways in which the component parts of a biquaternion may be manipulated algebraically. 1 Introduction It is typical of quaternion formulae that, though they be difficult to find, once found they are immediately verifiable. J. L. Synge (1972) [43, p34] arXiv:1001.0240v1 [math.RA] 1 Jan 2010 The quaternions are relatively well-known but the quaternions with complex components (complexified quaternions, or biquaternions1) are less so. This paper aims to set out the fundamental definitions of biquaternions and some elementary results, which, although elementary, are often not trivial. The emphasis in this paper is on the biquaternions as an applied algebra – that is, a tool for the manipulation ∗This paper was started in 2005 at the Laboratoire des Images et des Signaux (now part of the GIPSA-Lab), Grenoble, France with financial support from the Royal Academy of Engineering of the United Kingdom and the Centre National de la Recherche Scientifique (CNRS).
  • The Rolling Ball Problem on the Sphere

    The Rolling Ball Problem on the Sphere

    S˜ao Paulo Journal of Mathematical Sciences 6, 2 (2012), 145–154 The rolling ball problem on the sphere Laura M. O. Biscolla Universidade Paulista Rua Dr. Bacelar, 1212, CEP 04026–002 S˜aoPaulo, Brasil Universidade S˜aoJudas Tadeu Rua Taquari, 546, CEP 03166–000, S˜aoPaulo, Brasil E-mail address: [email protected] Jaume Llibre Departament de Matem`atiques, Universitat Aut`onomade Barcelona 08193 Bellaterra, Barcelona, Catalonia, Spain E-mail address: [email protected] Waldyr M. Oliva CAMGSD, LARSYS, Instituto Superior T´ecnico, UTL Av. Rovisco Pais, 1049–0011, Lisbon, Portugal Departamento de Matem´atica Aplicada Instituto de Matem´atica e Estat´ıstica, USP Rua do Mat˜ao,1010–CEP 05508–900, S˜aoPaulo, Brasil E-mail address: [email protected] Dedicated to Lu´ıs Magalh˜aes and Carlos Rocha on the occasion of their 60th birthdays Abstract. By a sequence of rolling motions without slipping or twist- ing along arcs of great circles outside the surface of a sphere of radius R, a spherical ball of unit radius has to be transferred from an initial state to an arbitrary final state taking into account the orientation of the ball. Assuming R > 1 we provide a new and shorter prove of the result of Frenkel and Garcia in [4] that with at most 4 moves we can go from a given initial state to an arbitrary final state. Important cases such as the so called elimination of the spin discrepancy are done with 3 moves only. 1991 Mathematics Subject Classification. Primary 58E25, 93B27. Key words: Control theory, rolling ball problem.
  • Vectors, Matrices and Coordinate Transformations

    Vectors, Matrices and Coordinate Transformations

    S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making extensive use of vectors in Dynamics, we will summarize some of their important properties. Vectors For our purposes we will think of a vector as a mathematical representation of a physical entity which has both magnitude and direction in a 3D space. Examples of physical vectors are forces, moments, and velocities. Geometrically, a vector can be represented as arrows. The length of the arrow represents its magnitude. Unless indicated otherwise, we shall assume that parallel translation does not change a vector, and we shall call the vectors satisfying this property, free vectors. Thus, two vectors are equal if and only if they are parallel, point in the same direction, and have equal length. Vectors are usually typed in boldface and scalar quantities appear in lightface italic type, e.g. the vector quantity A has magnitude, or modulus, A = |A|. In handwritten text, vectors are often expressed using the −→ arrow, or underbar notation, e.g. A , A. Vector Algebra Here, we introduce a few useful operations which are defined for free vectors. Multiplication by a scalar If we multiply a vector A by a scalar α, the result is a vector B = αA, which has magnitude B = |α|A. The vector B, is parallel to A and points in the same direction if α > 0.
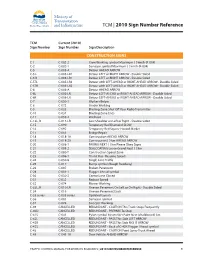
  • 2010 Sign Number Reference for Traffic Control Manual

    2010 Sign Number Reference for Traffic Control Manual

    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
  • Introduction Into Quaternions for Spacecraft Attitude Representation

    Introduction Into Quaternions for Spacecraft Attitude Representation

    Introduction into quaternions for spacecraft attitude representation Dipl. -Ing. Karsten Groÿekatthöfer, Dr. -Ing. Zizung Yoon Technical University of Berlin Department of Astronautics and Aeronautics Berlin, Germany May 31, 2012 Abstract The purpose of this paper is to provide a straight-forward and practical introduction to quaternion operation and calculation for rigid-body attitude representation. Therefore the basic quaternion denition as well as transformation rules and conversion rules to or from other attitude representation parameters are summarized. The quaternion computation rules are supported by practical examples to make each step comprehensible. 1 Introduction Quaternions are widely used as attitude represenation parameter of rigid bodies such as space- crafts. This is due to the fact that quaternion inherently come along with some advantages such as no singularity and computationally less intense compared to other attitude parameters such as Euler angles or a direction cosine matrix. Mainly, quaternions are used to • Parameterize a spacecraft's attitude with respect to reference coordinate system, • Propagate the attitude from one moment to the next by integrating the spacecraft equa- tions of motion, • Perform a coordinate transformation: e.g. calculate a vector in body xed frame from a (by measurement) known vector in inertial frame. However, dierent references use several notations and rules to represent and handle attitude in terms of quaternions, which might be confusing for newcomers [5], [4]. Therefore this article gives a straight-forward and clearly notated introduction into the subject of quaternions for attitude representation. The attitude of a spacecraft is its rotational orientation in space relative to a dened reference coordinate system.
  • Molecular Symmetry

    Molecular Symmetry

    Molecular Symmetry Symmetry helps us understand molecular structure, some chemical properties, and characteristics of physical properties (spectroscopy) – used with group theory to predict vibrational spectra for the identification of molecular shape, and as a tool for understanding electronic structure and bonding. Symmetrical : implies the species possesses a number of indistinguishable configurations. 1 Group Theory : mathematical treatment of symmetry. symmetry operation – an operation performed on an object which leaves it in a configuration that is indistinguishable from, and superimposable on, the original configuration. symmetry elements – the points, lines, or planes to which a symmetry operation is carried out. Element Operation Symbol Identity Identity E Symmetry plane Reflection in the plane σ Inversion center Inversion of a point x,y,z to -x,-y,-z i Proper axis Rotation by (360/n)° Cn 1. Rotation by (360/n)° Improper axis S 2. Reflection in plane perpendicular to rotation axis n Proper axes of rotation (C n) Rotation with respect to a line (axis of rotation). •Cn is a rotation of (360/n)°. •C2 = 180° rotation, C 3 = 120° rotation, C 4 = 90° rotation, C 5 = 72° rotation, C 6 = 60° rotation… •Each rotation brings you to an indistinguishable state from the original. However, rotation by 90° about the same axis does not give back the identical molecule. XeF 4 is square planar. Therefore H 2O does NOT possess It has four different C 2 axes. a C 4 symmetry axis. A C 4 axis out of the page is called the principle axis because it has the largest n . By convention, the principle axis is in the z-direction 2 3 Reflection through a planes of symmetry (mirror plane) If reflection of all parts of a molecule through a plane produced an indistinguishable configuration, the symmetry element is called a mirror plane or plane of symmetry .
  • (II) I Main Topics a Rotations Using a Stereonet B

    (II) I Main Topics a Rotations Using a Stereonet B

    GG303 Lecture 11 9/4/01 1 ROTATIONS (II) I Main Topics A Rotations using a stereonet B Comments on rotations using stereonets and matrices C Uses of rotation in geology (and engineering) II II Rotations using a stereonet A Best uses 1 Rotation axis is vertical 2 Rotation axis is horizontal (e.g., to restore tilted beds) B Construction technique 1 Find orientation of rotation axis 2 Find angle of rotation and rotate pole to plane (or a linear feature) along a small circle perpendicular to the rotation axis. a For a horizontal rotation axis the small circle is vertical b For a vertical rotation axis the small circle is horizontal 3 WARNING: DON'T rotate a plane by rotating its dip direction vector; this doesn't work (see handout) IIIComments on rotations using stereonets and matrices Advantages Disadvantages Stereonets Good for visualization Relatively slow Can bring into field Need good stereonets, paper Matrices Speed and flexibility Computer really required to Good for multiple rotations cut down on errors A General comments about stereonets vs. rotation matrices 1 With stereonets, an object is usually considered to be rotated and the coordinate axes are held fixed. 2 With rotation matrices, an object is usually considered to be held fixed and the coordinate axes are rotated. B To return tilted bedding to horizontal choose a rotation axis that coincides with the direction of strike. The angle of rotation is the negative of the dip of the bedding (right-hand rule! ) if the bedding is to be rotated back to horizontal and positive if the axes are to be rotated to the plane of the tilted bedding.
  • Glossary of Linear Algebra Terms

    Glossary of Linear Algebra Terms

    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
  • Chapter 5 ANGULAR MOMENTUM and ROTATIONS

    Chapter 5 ANGULAR MOMENTUM and ROTATIONS

    Chapter 5 ANGULAR MOMENTUM AND ROTATIONS In classical mechanics the total angular momentum L~ of an isolated system about any …xed point is conserved. The existence of a conserved vector L~ associated with such a system is itself a consequence of the fact that the associated Hamiltonian (or Lagrangian) is invariant under rotations, i.e., if the coordinates and momenta of the entire system are rotated “rigidly” about some point, the energy of the system is unchanged and, more importantly, is the same function of the dynamical variables as it was before the rotation. Such a circumstance would not apply, e.g., to a system lying in an externally imposed gravitational …eld pointing in some speci…c direction. Thus, the invariance of an isolated system under rotations ultimately arises from the fact that, in the absence of external …elds of this sort, space is isotropic; it behaves the same way in all directions. Not surprisingly, therefore, in quantum mechanics the individual Cartesian com- ponents Li of the total angular momentum operator L~ of an isolated system are also constants of the motion. The di¤erent components of L~ are not, however, compatible quantum observables. Indeed, as we will see the operators representing the components of angular momentum along di¤erent directions do not generally commute with one an- other. Thus, the vector operator L~ is not, strictly speaking, an observable, since it does not have a complete basis of eigenstates (which would have to be simultaneous eigenstates of all of its non-commuting components). This lack of commutivity often seems, at …rst encounter, as somewhat of a nuisance but, in fact, it intimately re‡ects the underlying structure of the three dimensional space in which we are immersed, and has its source in the fact that rotations in three dimensions about di¤erent axes do not commute with one another.
  • Hypercomplex Numbers

    Hypercomplex Numbers

    Hypercomplex numbers Johanna R¨am¨o Queen Mary, University of London [email protected] We have gradually expanded the set of numbers we use: first from finger counting to the whole set of positive integers, then to positive rationals, ir- rational reals, negatives and finally to complex numbers. It has not always been easy to accept new numbers. Negative numbers were rejected for cen- turies, and complex numbers, the square roots of negative numbers, were considered impossible. Complex numbers behave like ordinary numbers. You can add, subtract, multiply and divide them, and on top of that, do some nice things which you cannot do with real numbers. Complex numbers are now accepted, and have many important applications in mathematics and physics. Scientists could not live without complex numbers. What if we take the next step? What comes after the complex numbers? Is there a bigger set of numbers that has the same nice properties as the real numbers and the complex numbers? The answer is yes. In fact, there are two (and only two) bigger number systems that resemble real and complex numbers, and their discovery has been almost as dramatic as the discovery of complex numbers was. 1 Complex numbers Complex numbers where discovered in the 15th century when Italian math- ematicians tried to find a general solution to the cubic equation x3 + ax2 + bx + c = 0: At that time, mathematicians did not publish their results but kept them secret. They made their living by challenging each other to public contests of 1 problem solving in which the winner got money and fame.