Eindhoven University of Technology MASTER Forecasting Spare Parts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Serviceability of Passenger Trains During Acquisition Projects
SERVICEABILITY OF PASSENGER TRAINS DURING ACQUISITION PROJECTS Jorge Eduardo Parada Puig SERVICEABILITY OF PASSENGER TRAINS DURING ACQUISITION PROJECTS DISSERTATION to obtain the degree of doctor at the University of Twente, on the authority of the rector magnificus, Prof. Dr. H. Brinksma, on account of the decision of the graduation committee, to be publicly defended on Wednesday the th of June at : by Jorge Eduardo Parada Puig born on the th of September in Mérida, Venezuela. This dissertation has been approved by the Supervisor: Prof.Dr.Ir. L.A.M. van Dongen and the Co-Supervisors: Dr.Ir. S. Hoekstra Dr.Ir. R.J.I. Basten SERVICEABILITY OF PASSENGER TRAINS DURING ACQUISITION PROJECTS Jorge Eduardo Parada Puig Dissertation Committee Chairman / Secretary Prof.dr. G.P.M.R. Dewulf Supervisor Prof.dr.ir. L.A.M. van Dongen Co-Supervisors Dr.ir. S. Hoekstra Dr.ir. R.J.I. Basten Members Prof.dr.ir. T. Tinga (UT, CTW) Prof.dr.ir. F.J.A.M. van Houten (UT, CTW) Prof.dr.ir. C. Witteveen (TU Delft, EWI) Prof.dr.ir. G.J.J.A.N. Jan van Houtum (TU/e, IEIS) Prof.dr.ir. D. Gerhard (TU Wien, MWB) This research is part of the “Rolling Stock Life Cycle Logistics” applied research and development program, funded by NS/NedTrain. Publisher: J.E. Parada Puig, Design Production and Management, University of Twente, P.O. Box , AE Enschede, The Netherlands Cover by J.E. Parada Puig The image of the front cover is a graphical representation of the indenture struc- ture of a train, and its optimal line replaceable unit definitions. -

NS Annual Report 2018
See www.nsannualreport.nl for the online version NS Annual Report 2018 Table of contents 2 In brief 4 2018 in a nutshell 8 Foreword by the CEO 12 The profile of NS 16 Our strategy Activities in the Netherlands 23 Results for 2018 27 The train journey experience 35 Operational performance 47 World-class stations Operations abroad 54 Abellio 56 Strategy 58 Abellio United Kingdom (UK) 68 Abellio Germany 74 Looking ahead NS Group 81 Report by the Supervisory Board 94 Corporate governance 100 Organisation of risk management 114 Finances in brief 126 Our impact on the environment and on society 134 NS as an employer in the Netherlands 139 Organisational improvements 145 Dialogue with our stakeholders 164 Scope and reporting criteria Financial statements 168 Financial statements 238 Company financial statements Other information 245 Combined independent auditor’s report on the financial statements and sustainability information 256 NS ten-year summary This annual report is published both Dutch and English. In the event of any discrepancies between the Dutch and English version, the Dutch version will prevail. 1 NS annual report 2018 In brief More satisfied 4.2 million trips by NS app gets seat passengers in the OV-fiets searcher Netherlands (2017: 3.1 million) On some routes, 86% gave travelling by passengers can see which train a score of 7 out of carriages have free seats 10 or higher Customer 95.1% chance of Clean trains: 68% of satisfaction with HSL getting a seat passengers gave a South score of 7 out of 10 (2017: 95.0%) or higher 83% of -
European Railways Combine
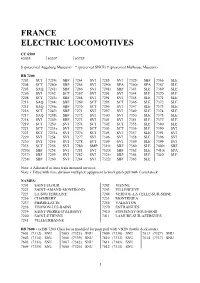
FRANCE ELECTRIC LOCOMOTIVES CC 6500 6503$ 6530* 6572# $ (preserved Augsburg Museum) * (preserved SNCF) # (preserved Mulhouse Museum) BB 7200 7203 SCT 7239r SBF 7264 SVI 7285 SVI 7323r SBF 7366 SLE 7204 SCT 7240r SBF 7265 SVI 7290r SPA 7340r SPA 7367 SLE 7205 SAQ 7241r SBF 7266 SVI 7291r SBF 7343 SLE 7369 SLE 7206 SVI 7242 SCT 7267 SVI 7293 SVI 7344 SLE 7370 SLE 7208 SCT 7243r SBF 7268 SVI 7294 SVI 7345 SLE 7371 SLE 7211 SAQ 7244r SBF 7269 SCT 7295 SCT 7346 SLE 7372 SLE 7215 SAQ 7246r SBF 7270 SCT 7296 SVI 7347 SLE 7373 SLE 7216 SCT 7247r SBF 7271 SVI 7297 SVI 7349 SLE 7374 SLE 7217 SAQ 7248r SBF 7272 SVI 7300 SVI 7350 SLE 7375 SLE 7218 SVI 7249r SBF 7273 SVI 7301 SVI 7351 SLE 7377 SLE 7219 SCT 7250 SVI 7274 SCT 7302 SCT 7355 SLE 7380 SLE 7221 SCT 7251a SVI 7275 SCT 7303 SCT 7356 SLE 7390 SVI 7223 SCT 7253a SVI 7276 SCT 7305 SVI 7357 SLE 7391 SVI 7229 SVI 7254 SVI 7277 SVI 7306 SVI 7358 SLE 7396 SVI 7230 SVI 7255 SVI 7278 SCT 7309 SVI 7359 SLE 7399 SVI 7235 SCT 7256 SVI 7280 SMP 7319r SBF 7360 SLE 7409r SBF 7236r SBF 7258 SVI 7281 SVI 7320r SBF 7362 SLE 7410r SPA 7237r SBF 7259 SVI 7282 SVI 7321r SBF 7364 SLE 7440 SLE 7238r SBF 7260 SVI 7284 SVI 7322r SBF 7365 SLE Note: a Allocated to Auto train motorail services Note: r Fitted with time division multiplex equipment to work push pull with Corail stock NAMES: 7203 SAINT-FLOUR 7242 VIENNE 7221 SAINT-AMAND-MONTROND 7243 VILLENEUVE 7223 LA SOUTERRAINE 7244 VERNOU-LA CELLE-SUR-SEINE 7236 CHAMBERY 7253 MONTREJEA 7237 PIERRELATTE 7256 VALENTON 7238 THONON-LES-BAINS 7270 ENTRAIGUES 7239 SAINT-PIERRE-D'ALBIGNY 7410 FONTENAY-SOUS-BOIS 7240 SAINT-ETIENNE 7411 LAMURE-SUR-AZERGUES 7241 VILLEURBANNE BB 7600 (ex BB 7200 Class locos modified for push pull with VB2N double deck stock) 7601 (7312) SNU 7605 (7325) SNU 7609 (7330) SNU 7613 (7327) SNU 7602 (7314) SNU 7606 (7339) SNU 7610 (7332) SNU 7614 (7337) SNU 7603 (7331) SNU 7607 (7342) SNU 7611 (7341) SNU 7604 (7335) SNU 7608 (7326) SNU 7612 (7311) SNU 5 BELGIUM DIESEL LOCOMOTIVES Class 50 Co-Co 5001 Saint-Gobain Works, Auvelais. -

STAMP Incident Investigation: Control Structures As a Tool to Intervene
STAMP Incident Investigation: Control Structures as a Tool to Intervene Rob Hoitsma Kirsten van Schaardenburgh Our goals today • To show you our use of STAMP during incident investigation • To share with you • the results so far • our recommendations Questions you migth have 1. Who is NEDTRAIN? 2. What is NEDTRAIN’s ‘traditional way’ of incident investigation? 3. Why did you introduce STAMP? 4. How did you apply STAMP? 5. Can you show us an example? 6. What are the results of using STAMP till now? 7. What would you recommend us? 1. NedTrain & NS NS: Operator & Owner rolling stock Amsterdam Daily inspection & cleaning Onnen 30 servicelocations Maastricht Amsterdam Leidschendam Groningen Line Maintenance Depot 30.000- 100.000 km Repairs Den Haag Maastricht Component R & O Overhaul Haarlem Overhaul and modernisations 15-20 years NedTrain: Subsidiary of Dutch Railways (NS) Damage repairs Maintenance, Repair & Overhaul of NS fleet 3100 emplyees 2. NEDTRAIN’s incident investigation Incidents & near misses: • Railtraffic (shunting), • Occupational health • Train safety Approx. 100 investigations/yr Proces: • Interviews • Data analysis • Multi Timeline & animation • Analysis & conclusions • Check & suggestions; by presenting to all involved • Measures & management learning; by presenting to management • New: STAMP analysis to improve last step 5 3. Reasons for introducing STAMP • Nancy’s lecture on STAMP in Amsterdam 2014 • Desire to include systems thinking in incident investigation • Desire to include mental models in incident investigation • Desire to change thinking of management • they did it wrong why did it make sense? • It’s up to the workfloor I have a stake! 6 4. Application of STAMP: context • Little experience in applying STAMP during incident investigation • at NEDTRAIN: none • in the Netherlands: limited, mainly Dutch Safety Board • No handbook • No training courses • Solution: hands-on coaching by experienced user, just start! 7 4. -

Eindhoven University of Technology MASTER an Aggregate Planning For
Eindhoven University of Technology MASTER An aggregate planning for preventive maintenance of bogies by NedTrain Vernooij, K. Award date: 2011 Link to publication Disclaimer This document contains a student thesis (bachelor's or master's), as authored by a student at Eindhoven University of Technology. Student theses are made available in the TU/e repository upon obtaining the required degree. The grade received is not published on the document as presented in the repository. The required complexity or quality of research of student theses may vary by program, and the required minimum study period may vary in duration. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain Eindhoven, July 2011 An Aggregate Planning for Preventive Maintenance of Bogies by NedTrain by Karin Vernooij BSc Industrial Engineering & Management Science (2009) Student Identity Number 0572650 in partial fulfilment of the requirements for the degree of Master of Science in Operations Management and Logistics Supervisors: Ir. B. Huisman, NedTrain Ir. dr. S.D.P. Flapper, TU/e, OPAC Prof. dr. ir. G.J. van Houtum, TU/e, OPAC Ir. J.J. Arts, TU/e, OPAC II TUE. -

Nedtrain.Pdf
Get Practiced: Op Snijvlak van Techniek en Proces! AMC Seminar 2013 Amersfoort, 10 oktober 2013 Prof.dr.ir. Leo A.M. van Dongen NedTrain Fleet Services Universiteit Twente Bedrijfsbrede Aanpak van Instandhouding Inhoud • Innovatieketen • Operational Excellence (zie AMC Seminar 2009) • Techniek terug op de agenda • Performance verbetering van materieel • Registreren, analyseren en bijsturen • Vergroting van voorspelbaarheid • Dynamisering van onderhoudsaanpak • Lerende organisatie Bijlagen: karakteristiek van NedTrain 2 Innovatieketen Vervoerders Leveranciers Energiebedrijven Architecten Consumenten Organisaties Aannemers Productie- proces Wetgeving Techniek Product Onderhouds- Kennisinstellingen proces Overheid Adviseurs Reizigers System Integrators Toezichthouders Service Providers Scheepswerven 3 Installateurs 2005-2010 Operationeel Proces op Orde! Reveil (1) Meer doen met minder maar betere middelen (55+ regeling) Aandacht voor primair proces: • Afleverkwaliteit (PQI), Kaizen, Lean Working, First Time Right • Veiligheid als voorwaarde • Opleidingen en sociale innovatie Vernieuwing van bedrijfsmiddelen (ca. 200 mio geïnvesteerd): • In/uitproces in Haarlem • Hispeed werkplaats in Watergraafsmeer • Wasmachines en servicelocaties Nijmegen, Utrecht, Eindhoven, Maastricht en Den Haag • Verhuizing in Rotterdam en Tilburg Boter bij de Vis Roadshow op locaties Medewerkers presenteren voor jury ideeën! 5 Onttrekking in Kort Cyclisch Onderhoud 6 Veiligheids DO Bespreking diverse veiligheidsonderwerpen Inspectierondes met terugkoppeling 7 Ontwikkeling -

Annual Report 2014
Annual Report 2014 See ns.nl/jaarverslag for the online version IN BRIEF First Public Transport Service Centres 4,100,000 opened in The Hague and Breda Journey Planner Xtra downloads 400,000 to 500,000 journey recommendations per day NEW More than 1,500,000 Button for feedback on overcrowding in the train trips by public transport bicycle 9 July 2014 76% of passengers give a score of Everyone in the Netherlands is using 7 out of 10 or higher the public transport smartcard for train travel for checking in and out Clean trains The target of 55% was not feasible because of the cleaners’ strike Trains are now running 2.2% more eciently 18,000 days of training have been INTERCITY BRUSSELS taken by our Certicate sta up from 12 to 16 times a day Mobility has a positive impact on society Punctuality 94.9% 94.9% of trains ran on time This was 93.6% in 2013 Journey times have a negative impact on society From 2018 onwards, all Dutch electric trains will be running on green electricity Prot in 2014 Investments in 2014 Revenue in 2014 180 million euros 461 million euros 4,144 million euros 100% Tackling overcrowding The ScotRail franchise was won 54 in the train in the United Kingdom signals passed 74.6% of passengers give -0.9% at danger 7 out of 10 or in 2014 higher 28,348 NS employees 2014 in a nutshell We took steps in 2014, together with other public transport carriers and stakeholders, to put the passenger even more at the centre of things. -

Lijst Van Verkortingen Spoorwegen 3E Druk P. Gutter
Lijst van Verkortingen Spoorwegen Peter Gutter September 2018 Sinds 2002 is deze spoorse verkortingenlijst als privé-project bijgehouden. De eerste versies van de lijst telden slechts enkele bladzijden en werden op informele wijze verspreid onder collega’s van onder meer ProRail, NS Reizigers, NedTrain, Strukton en Railion, die er dankbaar gebruik van maakten. Al gauw kreeg ik vele aanvullingen toegestuurd. De lijst groeide daardoor snel en dit is alweer de 20e bijgewerkte en herziene versie, die hierbij als 3e druk in (elektronische) boekvorm verschijnt. Boven de bladzijden heb ik echter wel de vermelding 20e versie laten staan, omdat er al zoveel exemplaren van vorige versies in omloop zijn. 1e druk, april 2012 2e uitgebreide en herziene druk, april 2015 3e uitgebreide en herziene druk, september 2018 CIP-GEGEVENS ISBN 978-90-818932-4-4 NUR 464 Uitgegeven via de website www.nvbs.com van de Postbus 1384, 3800 BJ Amersfoort © Peter Gutter 2018 Deze uitgave is met de meeste zorg samengesteld. Indien deze toch onjuistheden blijkt te bevatten, kunnen uitgever en auteur daarvoor geen aansprakelijkheid aanvaarden. Aan deze uitgave kunnen geen rechten worden ontleend. Overname van gegevens uit deze uitgave is toegestaan mits de bron wordt vermeld. Inleiding Het Nederlandse spoorbedrijf hangt letterlijk aan elkaar van de afkortingen (ofwel verkortingen, zoals ze bij het spoor genoemd worden). Dat stamt nog uit de tijd dat gegevens bij de spoorwegen telegrafisch werden overgeseind. De verkorting Asdm bijvoorbeeld, is nu eenmaal sneller over te seinen dan de volledige benaming Amsterdam Muiderpoort. Lange tijd werden de verkortingen door de NS bijgehouden in een officiële lijst, genaamd LV ofwel de Lijst van Verkortingen C 0405. -

NS Annual Report 2020
NS Annual report 2020 See www.nsannualreport.nl for the online version The NS Annual Report 2020 is published in Dutch and English. In the event of discrepancies between the versions, the Dutch version prevails. Table of contents 3 In Brief 4 Foreword by the CEO 7 2020: A year dominated by COVID-19 15 Our strategy 19 Expected developments in the long term 21 How NS adds value to society 25 Our impact on the Netherlands 31 The profile of NS 36 Compensation for victims of WWII transports Our activities and achievements in the Netherlands 38 Our performance on the main rail network and the high-speed line 40 Customer satisfaction with the main rail network and the high-speed line 44 Performance on the main rail network and the high-speed line 49 Door-to-door journey 53 Stations and their environment 59 Travelling and working in safety 63 Performance on sustainability 71 Attractive and inclusive employer Our activities and achievements abroad 78 Abellio 84 Abellio UK 99 Abellio Germany Financial performance 108 Finance in brief NS Group 116 Report of the Supervisory Board 129 Corporate governance 134 Risk management 141 Organisational improvements 145 Dialogue with our stakeholders in the Netherlands 160 Notes to the material themes 162 About the scope of this report 164 Scope and reporting criteria Financial statements 167 Consolidated financial statements 244 Company financial statements Other information 248 Other information 248 Combined independent auditor’s report and assurance report 263 NS ten-year summary 265 Disclaimer 2 | In Brief 3 | Foreword by the CEO Over the past year, NS has proved to be a healthy company that is able to keep the Netherlands moving despite huge setbacks. -

Annual Report Diversity & Inclusion 2013
Annual report diversity & inclusion 2013 Foreword We are pleased to commend to you our NS Group annual report detailing progress in journey, at the stage of ‘conscious incompetence’ if you prefer. This is however a furthering our collective efforts to promote diversity and inclusion across our challenge we shall embrace, with confidence that 2014 and beyond will see us businesses including, for the first time, Abellio. adopting a comprehensive diversity and inclusion framework across the Group, measuring our progress and promoting leadership accountability for improvement as Within Abellio, we chose ‘Inclusive’ as one of our 4 core values for good reasons. We a key business priority. know that to engage effectively with a very diverse passenger base, our workforce needs to be much more representative of the communites we serve – at all levels of the organisation. We also believe that diversity among employees leads to diversity of thought, which is the foundation for innovation - one of our areas of excellence and This Annual Report paints a picture of diversity and inclusion across the NS Group of the lifeblood for our future growth. The culture we want to create within Abellio which Abellio is a part. We hope that it will encourage you to work enthusiastically therefore is not so much a ‘melting pot’ of employees from diverse backgrounds and towards making diversity and inclusion a reality in the workplace. identities but rather a ‘stir fry’ where we value and embrace the difference and unique perspective that each of our people bring to their work. As you can see from the report, there are many examples of good practice across the broader Group and our own Operating Companies which provide a great source of inspiration but we recognise also that a more holistic approach is required and this needs to become a business and leadership priority – not a series of initiatives emanating from our HR functions. -

The Japanisation of the Dutch Railways
商 経 学 叢 第57巻 第3号2011年3月 Journal of Business Studies Vol. 57, No. 3, March 2011 The Japanisation of the Dutch Railways Didier M. van de Velde Abstract This paper presents the last two decades of exchanges between Japan and the Netherlands in the railway sector, under the generous help of professor Saito. The paper gives an overview of the publications and concrete implemented lessons that have resulted from these exchanges. A major part of the paper reports on extensive explorative interviews held with top and senior representatives of the Dutch railway sector who visited Japan during the last two decades. The paper re- ports on their perceptions of the Japanese lessons and gives an outlook on what they expect for the coming years. The paper closes with general conclusions about this learning process. 概 要 本 稿 で は,斎 藤 峻 彦 先 生 の 寛 大 な ご支 援 の も と,最 近20年 の 間 に進 め られ た,日 本 と オ ラ ンダ の 鉄 道 に 関 す る交 流 に つ い て 論 じる。 ま ず は,こ う した交 流 の 成 果 で あ る 出版 物 や,具 体 的 か つ 実 践 済 み の 教 訓 を 概 観 す る。 本 稿 の 中 心 は,こ こ20年 の 間 に 日本 を 訪 れ た オ ラ ン ダの 鉄 道 の 経 営 者 な らび に管 理 職 に対 して 実 施 した イ ン タ ビ ュー 結 果 を ま とめ た もの で あ る。 ま た,日 本 か ら得 た 教 訓 に対 して オ ラ ンダ が 持 って い る認 識 お よ び,近 い 将 来 にお け る課 題 を 示 す 。 最 後 に,一 連 の 学 習 プ ロセ ス につ い て ま とめ る。(訳:高 橋 愛 典) Key words Railway management; continuous improvement; international learn- ing; Dutch railways; Japanese railways JEL classification L30, L92, 033 March 15, 2011 accepted Vol. -

Review Op Aanpak Te Drukke Treinen NS
Eindrapport Review op aanpak te drukke treinen NS Datum april Opdrachtgever Ministerie van Infrastructuur en Milieu Contact Robert-Jaap Voorn Referentie GI- -!(R.$) Inhoud Inleiding . Aanleiding voor review ....................................................................................................... ! . Vraagstelling van review ..................................................................................................... ! . Scope van review ................................................................................................................ .! Aanpak van review .............................................................................................................. . Leeswijzer ............................................................................................................................ Bevindingen review . Algemene bevindingen ....................................................................................................... . Bevindingen per cluster van maatregelen ....................................................................... . Effecten op vervoercapaciteit en klantbeleving .............................................................. 5 .! Overwogen, maar niet genomen maatregelen ................................................................ Aanvullende maatregelen . Zoekrichtingen voor lange termijn ................................................................................... . Initiatieven voor korte termijn ........................................................................................