Specific Energy Limit and Its Influence on the Nature of Black Holes Javier Viaña
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Energy and the Hydrogen Economy
Energy and the Hydrogen Economy Ulf Bossel Fuel Cell Consultant Morgenacherstrasse 2F CH-5452 Oberrohrdorf / Switzerland +41-56-496-7292 and Baldur Eliasson ABB Switzerland Ltd. Corporate Research CH-5405 Baden-Dättwil / Switzerland Abstract Between production and use any commercial product is subject to the following processes: packaging, transportation, storage and transfer. The same is true for hydrogen in a “Hydrogen Economy”. Hydrogen has to be packaged by compression or liquefaction, it has to be transported by surface vehicles or pipelines, it has to be stored and transferred. Generated by electrolysis or chemistry, the fuel gas has to go through theses market procedures before it can be used by the customer, even if it is produced locally at filling stations. As there are no environmental or energetic advantages in producing hydrogen from natural gas or other hydrocarbons, we do not consider this option, although hydrogen can be chemically synthesized at relative low cost. In the past, hydrogen production and hydrogen use have been addressed by many, assuming that hydrogen gas is just another gaseous energy carrier and that it can be handled much like natural gas in today’s energy economy. With this study we present an analysis of the energy required to operate a pure hydrogen economy. High-grade electricity from renewable or nuclear sources is needed not only to generate hydrogen, but also for all other essential steps of a hydrogen economy. But because of the molecular structure of hydrogen, a hydrogen infrastructure is much more energy-intensive than a natural gas economy. In this study, the energy consumed by each stage is related to the energy content (higher heating value HHV) of the delivered hydrogen itself. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Superconducting Magnetic Energy Storage and Superconducting Self-Supplied Electromagnetic Launcher★
Eur. Phys. J. Appl. Phys. 80, 20901 (2017) THE EUROPEAN © EDP Sciences, 2017 PHYSICAL JOURNAL DOI: 10.1051/epjap/2017160452 APPLIED PHYSICS Regular Article Superconducting magnetic energy storage and superconducting self-supplied electromagnetic launcher★ Jérémie Ciceron*, Arnaud Badel, and Pascal Tixador Institut Néel, G2ELab CNRS/Université Grenoble Alpes, Grenoble, France Received: 5 December 2016 / Received in final form: 8 April 2017 / Accepted: 16 August 2017 Abstract. Superconductors can be used to build energy storage systems called Superconducting Magnetic Energy Storage (SMES), which are promising as inductive pulse power source and suitable for powering electromagnetic launchers. The second generation of high critical temperature superconductors is called coated conductors or REBCO (Rare Earth Barium Copper Oxide) tapes. Their current carrying capability in high magnetic field and their thermal stability are expanding the SMES application field. The BOSSE (Bobine Supraconductrice pour le Stockage d’Energie) project aims to develop and to master the use of these superconducting tapes through two prototypes. The first one is a SMES with high energy density. Thanks to the performances of REBCO tapes, the volume energy and specific energy of existing SMES systems can be surpassed. A study has been undertaken to make the best use of the REBCO tapes and to determine the most adapted topology in order to reach our objective, which is to beat the world record of mass energy density for a superconducting coil. This objective is conflicting with the classical strategies of superconducting coil protection. A different protection approach is proposed. The second prototype of the BOSSE project is a small-scale demonstrator of a Superconducting Self-Supplied Electromagnetic Launcher (S3EL), in which a SMES is integrated around the launcher which benefits from the generated magnetic field to increase the thrust applied to the projectile. -

Specific Energy
Quantum Mechanics_Specific energy Specific energy SI unit J/kg In SI base units m2/s2 Derivations from other quantities e = E/m Energy density has tables of specific energies of devices and materials. Specific energy is energy per unit mass. (It is also sometimes called "energy density," though "energy density" more precisely means energy per unit volume.) It is used to quantify, for example, stored heat or other thermodynamic propertiesof substances such as specific internal energy, specific enthalpy, specific Gibbs free energy, and specific Helmholtz free energy. It may also be used for the kinetic energy or potential energy of a body. Specific energy is an intensive property, whereas energy and mass are extensive properties. The SI unit for specific energy is the joule per kilogram (J/kg). Other units still in use in some contexts are the kilocalorie per gram (Cal/g or kcal/g), mostly in food-related topics, watt hours per kilogram in the field of batteries, and theImperial unit BTU per pound (BTU/lb), in some engineering and applied technical fields.[1] The gray and sievert are specialized measures for specific energy absorbed by body tissues in the form of radiation. The following table shows the factors for converting to J/kg: Unit SI equivalent kcal/g[2] 4.184 MJ/kg Wh/kg 3.6 kJ/kg kWh/kg 3.6 MJ/kg Btu/lb[3] 2.326 kJ/kg Btu/lb[4] ca. 2.32444 kJ/kg The concept of specific energy is related to but distinct from the chemical notion of molar energy, that is energy per mole of a substance. -

The International System of Units (SI)
NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303. -

From Cell to Battery System in Bevs: Analysis of System Packing Efficiency and Cell Types
Article From Cell to Battery System in BEVs: Analysis of System Packing Efficiency and Cell Types Hendrik Löbberding 1,* , Saskia Wessel 2, Christian Offermanns 1 , Mario Kehrer 1 , Johannes Rother 3, Heiner Heimes 1 and Achim Kampker 1 1 Chair for Production Engineering of E-Mobility Components, RWTH Aachen University, 52064 Aachen, Germany; c.off[email protected] (C.O.); [email protected] (M.K.); [email protected] (H.H.); [email protected] (A.K.) 2 Fraunhofer IPT, 48149 Münster, Germany; [email protected] 3 Faculty of Mechanical Engineering, RWTH Aachen University, 52072 Aachen, Germany; [email protected] * Correspondence: [email protected] Received: 7 November 2020; Accepted: 4 December 2020; Published: 10 December 2020 Abstract: The motivation of this paper is to identify possible directions for future developments in the battery system structure for BEVs to help choosing the right cell for a system. A standard battery system that powers electrified vehicles is composed of many individual battery cells, modules and forms a system. Each of these levels have a natural tendency to have a decreased energy density and specific energy compared to their predecessor. This however, is an important factor for the size of the battery system and ultimately, cost and range of the electric vehicle. This study investigated the trends of 25 commercially available BEVs of the years 2010 to 2019 regarding their change in energy density and specific energy of from cell to module to system. Systems are improving. However, specific energy is improving more than energy density. -
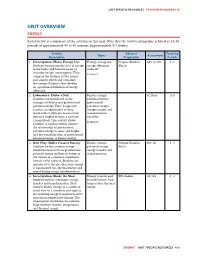
Unit Overview Energy
UNIT SPECIFIC RESOURCES TEACHER RESOURCES IV UNIT OVERVIEW ENERGY Listed below is a summary of the activities in this unit. Note that the total teaching time is listed as 23-35 periods of approximately 45 to 50 minutes (approximately 5-7 weeks). Activity Advance Teaching Topics Assessment Description Preparation Periods 1. Investigation: Home Energy Use Energy, energy use, Prepare Student E&T QC A5 1–2 Students brainstorm the uses of energy energy effciency, Sheets. in the home and become aware of trade-off everyday energy consumption. They LITERACY compare the features of two homes and suggest which one consumes less energy. Students then develop an operational defnition of energy effciency. 2. Laboratory: Drive a Nail Kinetic energy, PCI Proc. 2–3 Students are introduced to the potential energy, concepts of kinetic and gravitational gravitational potential energy. They design and potential energy, conduct an experiment to drop energy transfer and metal rods of different masses from transformation, different heights to drive a nail into variables a foam block. This activity allows LITERACY students to explore energy transfer, the relationship of gravitational potential energy to mass and height, and the transformation of gravitational potential energy to kinetic energy. 3. Role Play: Roller Coaster Energy Kinetic energy, Prepare Student EXP: A1 1–2 Students further examine energy potential energy, Sheet. transformations between gravitational energy transfer and potential energy and kinetic energy in transformation the context of a common experience— namely, roller coasters. Students are introduced to the idea that some energy is transformed into thermal energy and sound during energy transformations. 4. -

Energy and Temperature Analysis in Grinding
Transactions on Engineering Sciences vol 44, © 2003 WIT Press, www.witpress.com, ISSN 1743-3533 Energy and temperature analysis in grinding W.B. Rowel, M.N. Morganl, A. Batakol & T. Jin2 I School of Engineering, Liverpool John Moores University, UK 2 S.I.MS. CranJield University, UK Abstract Energy consumption and dissipation are discussed, leading into a thermal model for grinding. The analysis developed over many years applies to shallow-cut conventional grinding processes and also to deep grinding processes. Energy analysis provides insights into the grinding process and suggests avenues for process improvements. The thermal model provides a good estimation of contact temperatures as well as temperatures on the finish surface. Case studies are presented to demonstrate how operational efficiency, component quality and removal rates are affected by process conditions. Examples are included for High Efficiency Deep Grinding (HEDG). HEDG is defined as deep grinding at high workspeeds and very high removal rates. Tawakoli [20], Klocke [21]. The contact between the workpiece and wheel is represented as a circular arc. Experiments show that high removal rates and absence of thermal damage can be achieved. HEDG can achieve low specific grinding energy compared with shallow grinding and creep grinding. The chips take away most of the heat generated in the grinding process. As in creep grinding, bum-out of the coolant causes a steep rise in contact temperature of the workpiece. 1 Introduction Cost, quality and productivity in grinding processes are all dependent on energy consumption and process efficiency. In an inefficient process, excessive heat leads to increased temperature rise in the workpiece causing problems with surface integrity and require more frequent interruptions of production. -

Astronomy 112: the Physics of Stars Class 6 Notes: Internal Energy And
Astronomy 112: The Physics of Stars Class 6 Notes: Internal Energy and Radiative Transfer In the last class we used the kinetic theory of gasses to understand the pressure of stellar material. The kinetic view is essential to generalizing the concept of pressure to the environ- ments found in stars, where gas can be relativistic, degenerate, or both. The goal of today’s class is to extend that kinetic picture by thinking about pressure in stars in terms of the associated energy content of the gas. This will let us understand how the energy flow in stars interacts with gas pressure, a crucial step toward building stellar models. I. Pressure and Energy A. The Relationship Between Pressure and Internal Energy The fundamental object we dealt with in the last class was the distribution of particle mometa, dn(p)/dp, which we calculated from the Boltzmann distribu- tion. Given this, we could compute the pressure. However, this distribution also corresponds to a specific energy content, since for particles that don’t have inter- nal energy states, internal energy is just the kinetic energy of particle motions. Given a distribution of particle momenta dn(p)/dp in some volume of space, the corresponding density of energy within that volume of space is Z ∞ dn(p) e = (p) dp, 0 dp where (p) is the energy of a particle with momentum p. It is often more conve- nient to think about the energy per unit mass than the energy per unit volume. The energy per unit mass is just e divided by the density: 1 Z ∞ dn(p) u = (p) dp. -

Thermodynamic Properties of Molecular Oxygen
NATIONAL BUREAU OF STANDARDS REPORT 2611 THERMODYNAMIC PROPERTIES OF MOLECULAR OXYGEN tv Harold ¥, Woolley Themodynamics Section Division of Heat and Power U. S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS U. S. DEPARTMENT OF COMMERCE Sinclair Weeks, Secretary NATIONAL BUREAU OF STANDARDS A. V. Astin, Director THE NATIONAL BUREAU OF STANDARDS The scope of activities of the National Bureau of Standards is suggested in the following listing of the divisions and sections engaged in technical work. In general, each section is engaged in special- ized research, development, and engineering in the field indicated by its title. A brief description of the activities, and of the resultant reports and publications, appears on the inside of the back cover of this report. Electricity. Resistance Measurements. Inductance and Capacitance. Electrical Instruments. Magnetic Measurements. Applied Electricity. Electrochemistry. Optics and Metrology. Photometry and Colorimetry. Optical Instruments. Photographic Technology. Length. Gage. Heat and Power. Temperature Measurements. Thermodynamics. Cryogenics. Engines and Lubrication. Engine Fuels. Cryogenic Engineering. Atomic and Radiation Physics. Spectroscopy. Radiometry. Mass Spectrometry. Solid State Physics. Electron Physics. Atomic Physics. Neutron Measurements. Infrared Spectroscopy. Nuclear Physics. Radioactivity. X-Rays. Betatron. Nucleonic Instrumentation. Radio- logical Equipment. Atomic Energy Commission Instruments Branch. Chemistry. Organic Coatings. Surface Cheipistry. Organic Chemistry. -

Thermodynamic Data
..................................APPENDIX A Thermodynamic data A.l Introduction The thermodynamic tables presented here for enthalpy and internal energy differ from those that are usually available, since they incorporate the enthalpy of formation. This means that there is no need for separate tabulations of calorific values, and it will be found that energy balances for combustion calculations are greatly simplified. The enthalpy of formation (t-.Hf) is perhaps more familiar to physical chemists than to engineers. The enthalpy of formation ( t-.Hf) of a substance is the standard reaction enthalpy for the formation of the compound from its elements in their reference state. The reference state of an element is its most stable state (for example, carbon atoms, but oxygen molecules) at a specified temperature and pressure, usually 298.15 K and a pressure of l bar. In the case of atoms that can exist in different forms, it is necessary to specify their form, for example, carbon is as graphite, not diamond. Combustion calculations are most readily undertaken by using absolute (some times known as sensible) internal energies or enthalpy. In steady-flow systems where there is displacement work then enthalpy should be used; this has been illustrated by figure 3.8. When there is no displacement work then internal energy should be used (figure 3.7). Consider now figure 3.8 in more detail. With an adiabatic combustion process from reactants (R) to products (P) the enthalpy is constant, but there is a substantial rise in temperature: (A.l) In the case of the isothermal combustion process (IR ~ IP) the temperature (T) is obviously constant, and the difference in enthalpy corresponds to the isobaric calorific value (-t-.Jfi,): t-.H~ = HR .T- HP,T (A.2) 582 Thermodynamic data A.2 Thermodynamic principles In the following sections, it will be seen how the thermodynamic data for internal energy, enthalpy, entropy and Gibbs function can all be determined from measurements of heat capacity and phase change enthalpies (or internal energies). -

Energy Absorption in Polymer Composite Materials for Automotive Crashworthiness
Energy Absorption in Polymer Composite Materials for Automotive Crashworthiness George C. Jacob* Material Science and Engineering Department University of Tennessee, Knoxville 434 Dougherty Engineering Knoxville, TN 37996 USA John F. Fellers Professor Material Science and Engineering Department University of Tennessee, Knoxville 608 Dougherty Engineering Knoxville, TN 37996 USA Srdan Simunovic Group Leader, Computational Material Science Computer Science and Mathematics Division Oak Ridge National Laboratory Post Office Box 2008, Bldg. 6025, MS-6359 Oak Ridge, TN 37831-6359 USA J. Michael Starbuck Composite Materials Technology Group Engineering Technology Division Oak Ridge National Laboratory Post Office Box 2009 Oak Ridge, TN 37831-8048 USA *Author to whom correspondence should be addressed. Phone Number: 865 576 7361 Fax Number: 865 574 8257 E-mail: [email protected] 1 ABSTRACT The energy absorption capability of a composite material is critical to developing improved human safety in an automotive crash. Energy absorption is dependent on many parameters like fiber type, matrix type, fiber architecture, specimen geometry, processing conditions, fiber volume fraction, and testing speed. Changes in these parameters can cause subsequent changes in the specific energy absorption of composite materials up to a factor of 2. This paper is a detailed review of the energy absorption characteristics in polymer composite materials. An attempt is made to draw together and categorize the work done in the field of composites energy absorption that has been published in the literature in order to better understand the effect of a particular parameter on the energy absorption capability of composite materials. A description of the various test methodologies and crushing modes in composite tubes is also presented.