Astronomy 112: the Physics of Stars Class 6 Notes: Internal Energy And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
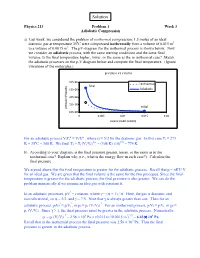
3-1 Adiabatic Compression
Solution Physics 213 Problem 1 Week 3 Adiabatic Compression a) Last week, we considered the problem of isothermal compression: 1.5 moles of an ideal diatomic gas at temperature 35oC were compressed isothermally from a volume of 0.015 m3 to a volume of 0.0015 m3. The pV-diagram for the isothermal process is shown below. Now we consider an adiabatic process, with the same starting conditions and the same final volume. Is the final temperature higher, lower, or the same as the in isothermal case? Sketch the adiabatic processes on the p-V diagram below and compute the final temperature. (Ignore vibrations of the molecules.) α α For an adiabatic process ViTi = VfTf , where α = 5/2 for the diatomic gas. In this case Ti = 273 o 1/α 2/5 K + 35 C = 308 K. We find Tf = Ti (Vi/Vf) = (308 K) (10) = 774 K. b) According to your diagram, is the final pressure greater, lesser, or the same as in the isothermal case? Explain why (i.e., what is the energy flow in each case?). Calculate the final pressure. We argued above that the final temperature is greater for the adiabatic process. Recall that p = nRT/ V for an ideal gas. We are given that the final volume is the same for the two processes. Since the final temperature is greater for the adiabatic process, the final pressure is also greater. We can do the problem numerically if we assume an idea gas with constant α. γ In an adiabatic processes, pV = constant, where γ = (α + 1) / α. -

Thermodynamics Formulation of Economics Burin Gumjudpai A
Thermodynamics Formulation of Economics 306706052 NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 Burin Gumjudpai A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics) School of Development Economics National Institute of Development Administration 2019 Thermodynamics Formulation of Economics Burin Gumjudpai School of Development Economics Major Advisor (Associate Professor Yuthana Sethapramote, Ph.D.) The Examining Committee Approved This Thesis Submitted in Partial 306706052 Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics). Committee Chairperson NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 (Assistant Professor Pongsak Luangaram, Ph.D.) Committee (Assistant Professor Athakrit Thepmongkol, Ph.D.) Committee (Associate Professor Yuthana Sethapramote, Ph.D.) Dean (Associate Professor Amornrat Apinunmahakul, Ph.D.) ______/______/______ ABST RACT ABSTRACT Title of Thesis Thermodynamics Formulation of Economics Author Burin Gumjudpai Degree Master of Economics (Financial Economics) Year 2019 306706052 We consider a group of information-symmetric consumers with one type of commodity in an efficient market. The commodity is fixed asset and is non-disposable. We are interested in seeing if there is some connection of thermodynamics formulation NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 to microeconomics. We follow Carathéodory approach which requires empirical existence of equation of state (EoS) and coordinates before performing maximization of variables. In investigating EoS of various system for constructing the economics EoS, unexpectedly new insights of thermodynamics are discovered. With definition of truly endogenous function, criteria rules and diagrams are proposed in identifying the status of EoS for an empirical equation. -

Specific Energy Limit and Its Influence on the Nature of Black Holes Javier Viaña
Specific Energy Limit and its Influence on the Nature of Black Holes Javier Viaña To cite this version: Javier Viaña. Specific Energy Limit and its Influence on the Nature of Black Holes. 2021. hal- 03322333 HAL Id: hal-03322333 https://hal.archives-ouvertes.fr/hal-03322333 Preprint submitted on 19 Aug 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 16th of August of 2021 Specific Energy Limit and its Influence on the Nature of Black Holes Javier Viaña [0000-0002-0563-784X] University of Cincinnati, Cincinnati OH 45219, USA [email protected] What if the universe has a limit on the amount of energy that a certain mass can have? This article explores this possibility and suggests a theory for the creation and nature of black holes based on an energetic limit. The Specific Energy Limit Energy is an extensive property, and we know that as we add more mass to a given system, we can easily increase its energy. Specific energy on the other hand is an intensive property. It is defined as the energy divided by the mass and it is measured in units of J/kg. -

Energy and the Hydrogen Economy
Energy and the Hydrogen Economy Ulf Bossel Fuel Cell Consultant Morgenacherstrasse 2F CH-5452 Oberrohrdorf / Switzerland +41-56-496-7292 and Baldur Eliasson ABB Switzerland Ltd. Corporate Research CH-5405 Baden-Dättwil / Switzerland Abstract Between production and use any commercial product is subject to the following processes: packaging, transportation, storage and transfer. The same is true for hydrogen in a “Hydrogen Economy”. Hydrogen has to be packaged by compression or liquefaction, it has to be transported by surface vehicles or pipelines, it has to be stored and transferred. Generated by electrolysis or chemistry, the fuel gas has to go through theses market procedures before it can be used by the customer, even if it is produced locally at filling stations. As there are no environmental or energetic advantages in producing hydrogen from natural gas or other hydrocarbons, we do not consider this option, although hydrogen can be chemically synthesized at relative low cost. In the past, hydrogen production and hydrogen use have been addressed by many, assuming that hydrogen gas is just another gaseous energy carrier and that it can be handled much like natural gas in today’s energy economy. With this study we present an analysis of the energy required to operate a pure hydrogen economy. High-grade electricity from renewable or nuclear sources is needed not only to generate hydrogen, but also for all other essential steps of a hydrogen economy. But because of the molecular structure of hydrogen, a hydrogen infrastructure is much more energy-intensive than a natural gas economy. In this study, the energy consumed by each stage is related to the energy content (higher heating value HHV) of the delivered hydrogen itself. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Superconducting Magnetic Energy Storage and Superconducting Self-Supplied Electromagnetic Launcher★
Eur. Phys. J. Appl. Phys. 80, 20901 (2017) THE EUROPEAN © EDP Sciences, 2017 PHYSICAL JOURNAL DOI: 10.1051/epjap/2017160452 APPLIED PHYSICS Regular Article Superconducting magnetic energy storage and superconducting self-supplied electromagnetic launcher★ Jérémie Ciceron*, Arnaud Badel, and Pascal Tixador Institut Néel, G2ELab CNRS/Université Grenoble Alpes, Grenoble, France Received: 5 December 2016 / Received in final form: 8 April 2017 / Accepted: 16 August 2017 Abstract. Superconductors can be used to build energy storage systems called Superconducting Magnetic Energy Storage (SMES), which are promising as inductive pulse power source and suitable for powering electromagnetic launchers. The second generation of high critical temperature superconductors is called coated conductors or REBCO (Rare Earth Barium Copper Oxide) tapes. Their current carrying capability in high magnetic field and their thermal stability are expanding the SMES application field. The BOSSE (Bobine Supraconductrice pour le Stockage d’Energie) project aims to develop and to master the use of these superconducting tapes through two prototypes. The first one is a SMES with high energy density. Thanks to the performances of REBCO tapes, the volume energy and specific energy of existing SMES systems can be surpassed. A study has been undertaken to make the best use of the REBCO tapes and to determine the most adapted topology in order to reach our objective, which is to beat the world record of mass energy density for a superconducting coil. This objective is conflicting with the classical strategies of superconducting coil protection. A different protection approach is proposed. The second prototype of the BOSSE project is a small-scale demonstrator of a Superconducting Self-Supplied Electromagnetic Launcher (S3EL), in which a SMES is integrated around the launcher which benefits from the generated magnetic field to increase the thrust applied to the projectile. -

Specific Energy
Quantum Mechanics_Specific energy Specific energy SI unit J/kg In SI base units m2/s2 Derivations from other quantities e = E/m Energy density has tables of specific energies of devices and materials. Specific energy is energy per unit mass. (It is also sometimes called "energy density," though "energy density" more precisely means energy per unit volume.) It is used to quantify, for example, stored heat or other thermodynamic propertiesof substances such as specific internal energy, specific enthalpy, specific Gibbs free energy, and specific Helmholtz free energy. It may also be used for the kinetic energy or potential energy of a body. Specific energy is an intensive property, whereas energy and mass are extensive properties. The SI unit for specific energy is the joule per kilogram (J/kg). Other units still in use in some contexts are the kilocalorie per gram (Cal/g or kcal/g), mostly in food-related topics, watt hours per kilogram in the field of batteries, and theImperial unit BTU per pound (BTU/lb), in some engineering and applied technical fields.[1] The gray and sievert are specialized measures for specific energy absorbed by body tissues in the form of radiation. The following table shows the factors for converting to J/kg: Unit SI equivalent kcal/g[2] 4.184 MJ/kg Wh/kg 3.6 kJ/kg kWh/kg 3.6 MJ/kg Btu/lb[3] 2.326 kJ/kg Btu/lb[4] ca. 2.32444 kJ/kg The concept of specific energy is related to but distinct from the chemical notion of molar energy, that is energy per mole of a substance. -

The First Law of Thermodynamics Continued Pre-Reading: §19.5 Where We Are
Lecture 7 The first law of thermodynamics continued Pre-reading: §19.5 Where we are The pressure p, volume V, and temperature T are related by an equation of state. For an ideal gas, pV = nRT = NkT For an ideal gas, the temperature T is is a direct measure of the average kinetic energy of its 3 3 molecules: KE = nRT = NkT tr 2 2 2 3kT 3RT and vrms = (v )av = = r m r M p Where we are We define the internal energy of a system: UKEPE=+∑∑ interaction Random chaotic between atoms motion & molecules For an ideal gas, f UNkT= 2 i.e. the internal energy depends only on its temperature Where we are By considering adding heat to a fixed volume of an ideal gas, we showed f f Q = Nk∆T = nR∆T 2 2 and so, from the definition of heat capacity Q = nC∆T f we have that C = R for any ideal gas. V 2 Change in internal energy: ∆U = nCV ∆T Heat capacity of an ideal gas Now consider adding heat to an ideal gas at constant pressure. By definition, Q = nCp∆T and W = p∆V = nR∆T So from ∆U = Q W − we get nCV ∆T = nCp∆T nR∆T − or Cp = CV + R It takes greater heat input to raise the temperature of a gas a given amount at constant pressure than constant volume YF §19.4 Ratio of heat capacities Look at the ratio of these heat capacities: we have f C = R V 2 and f + 2 C = C + R = R p V 2 so C p γ = > 1 CV 3 For a monatomic gas, CV = R 3 5 2 so Cp = R + R = R 2 2 C 5 R 5 and γ = p = 2 = =1.67 C 3 R 3 YF §19.4 V 2 Problem An ideal gas is enclosed in a cylinder which has a movable piston. -

Adiabatic Bulk Moduli
8.03 at ESG Supplemental Notes Adiabatic Bulk Moduli To find the speed of sound in a gas, or any property of a gas involving elasticity (see the discussion of the Helmholtz oscillator, B&B page 22, or B&B problem 1.6, or French Pages 57-59.), we need the “bulk modulus” of the fluid. This will correspond to the “spring constant” of a spring, and will give the magnitude of the restoring agency (pressure for a gas, force for a spring) in terms of the change in physical dimension (volume for a gas, length for a spring). It turns out to be more useful to use an intensive quantity for the bulk modulus of a gas, so what we want is the change in pressure per fractional change in volume, so the bulk modulus, denoted as κ (the Greek “kappa” which, when written, has a great tendency to look like k, and in fact French uses “K”), is ∆p dp κ = − , or κ = −V . ∆V/V dV The minus sign indicates that for normal fluids (not all are!), a negative change in volume results in an increase in pressure. To find the bulk modulus, we need to know something about the gas and how it behaves. For our purposes, we will need three basic principles (actually 2 1/2) which we get from thermodynamics, or the kinetic theory of gasses. You might well have encountered these in previous classes, such as chemistry. A) The ideal gas law; pV = nRT , with the standard terminology. B) The first law of thermodynamics; dU = dQ − pdV,whereUis internal energy and Q is heat. -

Session 15 Thermodynamics
Session 15 Thermodynamics Cheryl Hurkett Physics Innovations Centre for Excellence in Learning and Teaching CETL (Leicester) Department of Physics and Astronomy University of Leicester 1 Contents Welcome .................................................................................................................................. 4 Session Authors .................................................................................................................. 4 Learning Objectives .............................................................................................................. 5 The Problem ........................................................................................................................... 6 Issues .................................................................................................................................... 6 Energy, Heat and Work ........................................................................................................ 7 The First Law of thermodynamics................................................................................... 8 Work..................................................................................................................................... 9 Heat .................................................................................................................................... 11 Principal Specific heats of a gas ..................................................................................... 12 Summary .......................................................................................................................... -

The International System of Units (SI)
NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303. -

From Cell to Battery System in Bevs: Analysis of System Packing Efficiency and Cell Types
Article From Cell to Battery System in BEVs: Analysis of System Packing Efficiency and Cell Types Hendrik Löbberding 1,* , Saskia Wessel 2, Christian Offermanns 1 , Mario Kehrer 1 , Johannes Rother 3, Heiner Heimes 1 and Achim Kampker 1 1 Chair for Production Engineering of E-Mobility Components, RWTH Aachen University, 52064 Aachen, Germany; c.off[email protected] (C.O.); [email protected] (M.K.); [email protected] (H.H.); [email protected] (A.K.) 2 Fraunhofer IPT, 48149 Münster, Germany; [email protected] 3 Faculty of Mechanical Engineering, RWTH Aachen University, 52072 Aachen, Germany; [email protected] * Correspondence: [email protected] Received: 7 November 2020; Accepted: 4 December 2020; Published: 10 December 2020 Abstract: The motivation of this paper is to identify possible directions for future developments in the battery system structure for BEVs to help choosing the right cell for a system. A standard battery system that powers electrified vehicles is composed of many individual battery cells, modules and forms a system. Each of these levels have a natural tendency to have a decreased energy density and specific energy compared to their predecessor. This however, is an important factor for the size of the battery system and ultimately, cost and range of the electric vehicle. This study investigated the trends of 25 commercially available BEVs of the years 2010 to 2019 regarding their change in energy density and specific energy of from cell to module to system. Systems are improving. However, specific energy is improving more than energy density.