Name Clustering on the Basis of Parental Preferences Gerrit Bloothooft and Loek Groot Utrecht University, the Netherlands
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
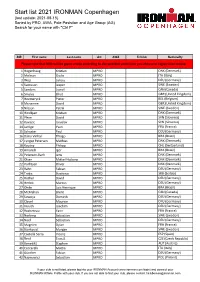
Start List 2021 IRONMAN Copenhagen (Last Update: 2021-08-15) Sorted by PRO, AWA, Pole Posistion and Age Group (AG) Search for Your Name with "Ctrl F"
Start list 2021 IRONMAN Copenhagen (last update: 2021-08-15) Sorted by PRO, AWA, Pole Posistion and Age Group (AG) Search for your name with "Ctrl F" BIB First name Last name AG AWA TriClub Nationallty Please note that BIBs will be given onsite according to the selected swim time you choose in registration oniste. 1 Hogenhaug Kristian MPRO DNK (Denmark) 2 Molinari Giulio MPRO ITA (Italy) 3 Wojt Lukasz MPRO DEU (Germany) 4 Svensson Jesper MPRO SWE (Sweden) 5 Sanders Lionel MPRO CAN (Canada) 6 Smales Elliot MPRO GBR (United Kingdom) 7 Heemeryck Pieter MPRO BEL (Belgium) 8 Mcnamee David MPRO GBR (United Kingdom) 9 Nilsson Patrik MPRO SWE (Sweden) 10 Hindkjær Kristian MPRO DNK (Denmark) 11 Plese David MPRO SVN (Slovenia) 12 Kovacic Jaroslav MPRO SVN (Slovenia) 14 Jarrige Yvan MPRO FRA (France) 15 Schuster Paul MPRO DEU (Germany) 16 Dário Vinhal Thiago MPRO BRA (Brazil) 17 Lyngsø Petersen Mathias MPRO DNK (Denmark) 18 Koutny Philipp MPRO CHE (Switzerland) 19 Amorelli Igor MPRO BRA (Brazil) 20 Petersen-Bach Jens MPRO DNK (Denmark) 21 Olsen Mikkel Hojborg MPRO DNK (Denmark) 22 Korfitsen Oliver MPRO DNK (Denmark) 23 Rahn Fabian MPRO DEU (Germany) 24 Trakic Strahinja MPRO SRB (Serbia) 25 Rother David MPRO DEU (Germany) 26 Herbst Marcus MPRO DEU (Germany) 27 Ohde Luis Henrique MPRO BRA (Brazil) 28 McMahon Brent MPRO CAN (Canada) 29 Sowieja Dominik MPRO DEU (Germany) 30 Clavel Maurice MPRO DEU (Germany) 31 Krauth Joachim MPRO DEU (Germany) 32 Rocheteau Yann MPRO FRA (France) 33 Norberg Sebastian MPRO SWE (Sweden) 34 Neef Sebastian MPRO DEU (Germany) 35 Magnien Dylan MPRO FRA (France) 36 Björkqvist Morgan MPRO SWE (Sweden) 37 Castellà Serra Vicenç MPRO ESP (Spain) 38 Řenč Tomáš MPRO CZE (Czech Republic) 39 Benedikt Stephen MPRO AUT (Austria) 40 Ceccarelli Mattia MPRO ITA (Italy) 41 Günther Fabian MPRO DEU (Germany) 42 Najmowicz Sebastian MPRO POL (Poland) If your club is not listed, please log into your IRONMAN Account (www.ironman.com/login) and connect your IRONMAN Athlete Profile with your club. -

The Art of Staying Neutral the Netherlands in the First World War, 1914-1918
9 789053 568187 abbenhuis06 11-04-2006 17:29 Pagina 1 THE ART OF STAYING NEUTRAL abbenhuis06 11-04-2006 17:29 Pagina 2 abbenhuis06 11-04-2006 17:29 Pagina 3 The Art of Staying Neutral The Netherlands in the First World War, 1914-1918 Maartje M. Abbenhuis abbenhuis06 11-04-2006 17:29 Pagina 4 Cover illustration: Dutch Border Patrols, © Spaarnestad Fotoarchief Cover design: Mesika Design, Hilversum Layout: PROgrafici, Goes isbn-10 90 5356 818 2 isbn-13 978 90 5356 8187 nur 689 © Amsterdam University Press, Amsterdam 2006 All rights reserved. Without limiting the rights under copyright reserved above, no part of this book may be reproduced, stored in or introduced into a retrieval system, or transmitted, in any form or by any means (electronic, mechanical, photocopying, recording or otherwise) without the written permission of both the copyright owner and the author of the book. abbenhuis06 11-04-2006 17:29 Pagina 5 Table of Contents List of Tables, Maps and Illustrations / 9 Acknowledgements / 11 Preface by Piet de Rooij / 13 Introduction: The War Knocked on Our Door, It Did Not Step Inside: / 17 The Netherlands and the Great War Chapter 1: A Nation Too Small to Commit Great Stupidities: / 23 The Netherlands and Neutrality The Allure of Neutrality / 26 The Cornerstone of Northwest Europe / 30 Dutch Neutrality During the Great War / 35 Chapter 2: A Pack of Lions: The Dutch Armed Forces / 39 Strategies for Defending of the Indefensible / 39 Having to Do One’s Duty: Conscription / 41 Not True Reserves? Landweer and Landstorm Troops / 43 Few -
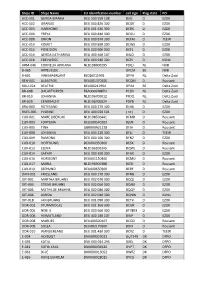
Ships ID Ships Name EU Identifcation Number Call Sign Flag State PO ACC
Ships ID Ships Name EU identifcation number call sign Flag state PO ACC-001 GERDA-BIANKA DEU 500 550 108 DJIG D EZDK ACC-002 URANUS DEU 000 820 300 DCGK D EZDK ACC-003 HARMONIE DEU 001 630 300 DCRK D EZDK ACC-004 FREYA DEU 000 840 300 DCGU D EZDK ACC-008 ORION DEU 000 870 300 DCFM D TEEW ACC-010 KOMET DEU 000 890 300 DCWK D EZDK ACC-012 POSEIDON DEU 000 900 300 DCFL D EZDK ACC-014 GERDA KATHARINA DEU 400 460 107 DIUO D EZDK ACC-016 EDELWEISS DEU 000 940 300 DCPJ D KüNo ARM-046 CORNELIA ADRIANA NLD198600295 PDQJ NL NVB B-065 ARTEVELDE OPCM BE NVB B-601 VAN MAERLANT BE026011991 OPYA NL Delta Zuid BEN-001 ALBATROS DEU001370300 DCQM D Rousant BOU-024 BEATRIX BEL000241964 OPAX BE Delta Zuid BR-008 DAUWTRIPPER FRA000648870 PCDV NL Delta Zuid BR-010 JOHANNA NLD196700012 PFDQ NL Delta Zuid BR-029 EENDRACHT NLD196700024 PDYB NL Delta Zuid BRA-003 ROTESAND DEU 000 270 300 DLHX D EZDK BUES-005 YVONNE DEU 404 020 101 ( nc ) D EZDK CUX-001 MARE LIBERUM NLD198500441 DFMD D Rousant CUX-003 FORTUNA DEU500540102 DJEN D Rousant CUX-005 TINA GBR000A21228 DFJH D Rousant CUX-008 JOHANNA DEU 000 220 300 DFLJ D TEEW CUX-009 RAMONA DEU 000 160 300 DFNZ D EZDK CUX-010 HOFFNUNG DEU000350300 DESX D Rousant CUX-012 ELENA NLD196300345 DQWL D Rousant CUX-014 SAPHIR DEU 000 360 300 DFAX D EZDK CUX-016 HORIZONT DEU001150300 DCMU D Rousant CUX-017 MARIA NLD196900388 DJED D Rousant CUX-019 SEEHUND DEU000650300 DERF D Rousant DAN-001 FRIESLAND DEU 000 170 300 DFNB D EZDK DIT-001 MARTHA BRUHNS DEU 002 070 300 DQQJ D EZDK DIT-003 STIENE BRUHNS DEU 002 060 300 DQNX D EZDK -

OSCE Economic and Environmental Forum
EEF.INF/1/15/Rev.1 27 January 2015 ENGLISH only Organization for Security and Co-operation in Europe FINAL List of Participants for the 23rd OSCE Economic and Environmental Forum “Water governance in the OSCE area – increasing security and stability through co-operation” FIRST PREPARATORY MEETING 26 - 27 January 2015, Vienna Please be informed that the deadline for corrections expired on 27 January 2015, 1 p.m. 23rd OSCE Economic and Environmental Forum First Preparatory Meeting Vienna, 26 - 27 January 2015 Mr/Ms First Name Family Name Title/Position/Rank E-mail Address DELEGATIONS ALBANIA Amb Spiro KOCI Ambassador Permanent Representative to the OSCE ALBANIA Mr Artan CANAJ Deputy Head of the Permanent Mission for OSCE [email protected] Affairs ALBANIA Mr Besnik BARAJ Member of Parliament [email protected] Committee on Productive Activities, Trade and Environment ALBANIA Ms Vjola SALIAGA Expert [email protected] Water Resources Policy Department Ministry of Environment GERMANY Ms Christine WEIL Deputy Permanent Representative to the OSCE GERMANY Mr Otto SCHNEIDER Counsellor [email protected] Permanent Mission to the OSCE GERMANY Ms Irja BERG Desk Officer [email protected] OSCE Division Ministry of Foreign Affairs UNITED STATES OF AMERICA Amb Daniel BAER Ambassador Chief of Mission to the OSCE UNITED STATES OF AMERICA Mr David SWALLEY OSCE Desk Officer [email protected] Office of European Security and Political Affairs Department of State UNITED STATES OF AMERICA Mr Rolf OLSEN Senior Technical Lead [email protected] -

Disclosure Summary for CME Learners ATS 2017 International Conference - Washington D.C
American Thoracic Society - Disclosure Summary for CME Learners ATS 2017 International Conference - Washington D.C. - May 19-24, 2017 1) RELEVANT COMMERCIAL INTERESTS DISCLOSED BY CME PLANNERS AND PRESENTERS Initial Report as of May 15, 2017 Use Adobe PDF "Find" option to search for specific name. Presenter disclosures may continue on a successive page, or begin on a preceding page. Agrawal, Rishi Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Boehringer Ingelheim b.v. Speaker Agusti, Alvar Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Almirall Research Support Speaker Advisory Committee Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest AstraZeneca Pharmaceuticals LP Speaker Advisory Committee Research Support Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Boehringer Ingelheim b.v. Advisory Committee Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest GlaxoSmithKline, LLC. Advisory Committee Research Support Speaker Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Teva Pharmaceuticals USA, Inc. Speaker Advisory Committee Research Support Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Novartis Pharma AG Speaker Advisory Committee Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Merck Sharp & Dohme Corporation Advisory Committee Research Support Speaker 1 of 106 Agusti, Alvar Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Menarini Speaker Research Support Akulian, Jason A. Name of Commercial Interest and Type(s) of Relationship with that Commercial Interest Veran Medical Technologies, Inc. -

Geslaagdenkrant 2016 2 HET BELANG VAN LIMBURG
wij zijn geslaagd! geslaagdenKRanT 2016 2 HET BELANG VAN LIMBURG aerts, Beringen. Handelswetenschappen en bedrijfskunde: Hogere ZeevaartscHool onderscheiding: ester swennen, genk. antwerpen Master in de Audiovisuele Kunsten Bachelor in het bedrijfsmanagement voldoende wijze: marieke stulens, Bilzen. onderscheiding: vladimir stonis, sint-truiden. Nautische Wetenschappen: onderscheiding: nele vandael, genk. voldoening: Hamza mouatassim, genk. Master in de Nautische Wetenschappen Onderwijs: onderscheiding: Jonathan vandenbossche, lommel. luca scHool oF arts Bachelor in het onderwijs: secundair onderwijs voldoening: marcella schetz, opitter. MA beeldende kunsten (Genk): erasmusHogescHool Sociaal-agogisch werk: Afstudeerrichting Fotografie Brussel met onderscheiding: Boumediene Belbachir, genk. Bachelor in de gezinswetenschappen op voldoende wijze: Jonas camps, Hechtel. onderscheiding: anne-martje Beckers, lummen; Kristel Management, Media & Maatschappij: cuyvers, Beringen; sara De Becker, Heers; nadine MA productdesign (Genk): Bachelor in het Communicatiemanagement Hermans, Dilsen-stokkem; an van lishout, Heusden- voldoende wijze: nele couwberghs, tessenderlo; Zolder; Dagmar vandebroek, Koersel. Afstudeerrichting Fotografie voldoening: marleen Bovie, tongeren; christine lavrey- maximiljaan van der Beken, Zonhoven. Katrijn caelen, genk. onderscheiding: mathijs vanduffel, overpelt. sen, Hasselt; valerie monnens, Heusden-Zolder; sandra Afstudeerrichting Communicatie- en Multime- vossen, Bocholt. Bachelor in het Hotelmanagement diadesign Bachelor -

Juilliard Dance
Juilliard Dance Senior Graduation Concert 2019 Welcome to Juilliard Dance Senior Graduation Concert 2019 Tonight, you will experience the culmination of a transformative four-year journey for the senior class of Juilliard Dance. Through rigorous physical training and artistic and intellectual exploration, all of the fourth-year dancers have expanded the possibilities of their movement abilities, stretching beyond what they thought possible when entering the program as freshmen. They have accepted the challenge of what it means to be a generous citizen artist and hold that responsibility close to their hearts. Chosen by the dancers, the solos and duets presented tonight have been commissioned for this evening or acquired from existing repertory and staged for this singular occasion. The works represent the manifestation of an evolution of growth and the discovery of their powerfully unique artistic voices. I am immensely proud of each and every fourth-year artist; it has been a joy and an honor to get to know the senior class, a group of individuals who will inevitably change the landscape of the field of dance as it exists today. Please join me for a standing ovation, cheering on the members of the class of 2019 as they take the stage for the last time together in the Peter Jay Sharp Theater. Well done, dancers—we thank you for your beautiful contributions to our Juilliard community and to the world beyond our campus. Sincerely, Little mortal jump Alicia Graf Mack Director, Juilliard Dance Cover: Alejandro Cerrudo's This page: Collaboration -
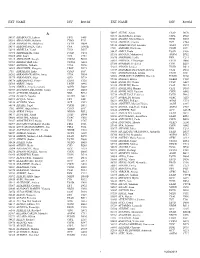
Ext Name Div Room Ext Name Div Room ______
EXT NAME DIV ROOM EXT NAME DIV ROOM __________________________________________________________________________________________________________________________ A 56407 ALUNG, Ashok CSAP D170 52673 ALVETRETI, Letizia CSPL D328 54157 ABABOUCH, Lahsen FIPX F405 54458 AMADO, Maria Blanca TCIB D503 55581 ABALSAMO, Stefania CIOO F713 53290 AMARAL, Cristina TCE C744 53264 ABBASSIAN, Abdolreza ESTD D804 55126 AMBROSIANO, Luciana AGDF C292 54511 ABBONDANZA, Carla CPA A143B 1709 AMEGEE, Emilienne CSSD SSC 52390 ABDELLA, Yesuf TCIA D557 56437 AMICI, Paolo ESSD C456 55396 ABDIRIZZAK, Tania FOED C474 53985 AMMATI, Mohammed AGPM B752 53485 ABE, Kaori TCE C751 54876 AMOROSO, Leslie ESN C214 54315 ABI NASSIF, Joseph CSDM B104 56891 AMROUK, El Mamoun ESTD D866 53963 ABI RACHED, Elie CPAM A281 53980 ANAMAN, Frederick CIOF B239 55087 ABITBOL, Nathalie TCIA D556 54213 ANAND, Sanjeev TCSD D611 56584 ABOU-RIZK, Margaret LEGP D371 53309 ANDARIAS DE PRADO, Rebeca CSAI D102 1716 ABRAHAM, Erika CSSD SSC 1725 ANDONOVSKA, Liljana CSSD SSC 56202 ABRAMO-GUARNA, Anna TCIA D554 53602 ANDRADE CIANFRINI, Graciela FOMD D468 55375 ABRAMOVA, Olga OSD D728 55742 ANELLO, Enrico OEKM C102 54178 ABRAMOVICI, Pierre CIOH C130 54441 ANGELINI, Chiara CPAP A487 56760 ABREU, Maria LEGD A442 54109 ANGELINI, Flavio CSAI D114 53296 ABRINA, Angelica Gavina OSPD B449 55313 ANGELONI, Marino CSAI D103 52709 ACCARDO-DELHOME, Jeanne FODP D435 53145 ANGELOZZI, Vanessa CSDU A042 53843 ACHOURI, Moujahed NRL B732 53720 ANGELUCCI, Federica ESTD D863 52294 ACOSTA, Natalia OEDD B452 52677 ANIBALDI, -

2018 Abstract Book
CONTENTS Table of Contents INFORMATION Continuing Medical Education .................................................................................................5 Guidelines for Speakers ..........................................................................................................6 Guidelines for Poster Presentations .........................................................................................8 SPEAKER ABSTRACTS Abstracts ...............................................................................................................................9 POSTER ABSTRACTS Basic Research (Location – Room 101) ...............................................................................63 Clinical (Location – Room 8) ..............................................................................................141 2018 Joint Global Neurofibromatosis Conference · Paris, France · November 2-6, 2018 | 3 4 | 2018 Joint Global Neurofibromatosis Conference · Paris, France · November 2-6, 2018 EACCME European Accreditation Council for Continuing Medical Education 2018 Joint Global Neurofibromatosis Conference Paris, France, 02/11/2018–06/11/2018 has been accredited by the European Accreditation Council for Continuing Medical Education (EACCME®) for a maximum of 27 European CME credits (ECMEC®s). Each medical specialist should claim only those credits that he/she actually spent in the educational activity. The EACCME® is an institution of the European Union of Medical Specialists (UEMS), www.uems.net. Through an agreement between -

Correspondence of Maria Van Rensselaer (1669-1689)
CORRESPONDENCE OF MARIA VAN RENSSELAER 1669-1689 Translated and edited by A. J. F. VAN LAER Archivist, Archives and History Division ALBANY THE UNIVERSITY OF THE STATE OF NEW YORK I 935 PREFACE In the preface to the Correspondence of Jeremias van Rens selaer, which was piiblished in 1932, attention was called to the fact that after the death of Jeremias van Rensselaer his widow carried on a regular correspondence with her husband's youngest brother, Richard van Rensselaer, in regard to the administration of the colony of Rensselaerswyck, and the plan was announced to publish this correspondence in another volume. This plan has been carried into effect in the present volume, which contains translations of all that has been preserved of the correspondence of Maria van Rensselaer, including besides the correspondence with her brother-in-law many letters which passed between her and her brother Stephanus van Cortlandt and other members of the Van Cortlandt family. Maria van Rensselaer was born at New York on July 20, 1645, and was the third child of Oloff Stevensen van Cortlandt and his wife Anna Loockermans. She married on July 12, 1662, when not quite 17 years of age, Jeremias van Rensselaer, who in 1658 had succeeded his brother Jan Baptist van Rensse laer as director of the colony of Rensselaerswyck. By him she had four sons and two daughters, her youngest son, Jeremias, being born shortly after her husband's death, which occurred on October 12, 1674. As at the time there was no one available who could succeed Jeremias van Rensselaer as director of the colony, the burden of its administration fell temporarily upon his widow, who in this emergency sought the advice of her brother Stephanus van Cortlandt. -

CONTENTS Journal VOLUME 42 / NUMBER 6 / DECEMBER 2013
EUROPEAN RESPIRATORY CONTENTS journal VOLUME 42 / NUMBER 6 / DECEMBER 2013 EDITORIALS 1433 The European Lung Corner Jean-Paul Sculier 1435 Putting noninvasive lung mechanics into context Peter M.A. Calverley and Ramon Farre 1438 The CFTR and EGFR relationship in airway vascular growth, and its importance in cystic fibrosis Jay A. Nadel 1441 Bronchodilator combinations for COPD: real hopes or a new Pandora’s box? Nicolas Roche and Pascal Chanez 1446 Clinical trials in idiopathic pulmonary fibrosis: a framework for moving forward David J. Lederer 1449 Therapeutic drug management: is it the future of multidrug-resistant tuberculosis treatment? Shashikant Srivastava, Charles A. Peloquin, Giovanni Sotgiu and Giovanni Battista Migliori 1454 Legionnaires’ disease in Europe: all quiet on the eastern front? Julien Beauté, Emmanuel Robesyn and Birgitta de Jong, on behalf of the European Legionnaires’ Disease Surveillance Network 1459 Avoiding overdiagnosis in lung cancer screening: the volume doubling time strategy Marie-Pierre Revel 1464 Does drug-induced emphysema exist? Norbert F. Voelkel, Shiro Mizuno and Masanori Yasuo European lung corner 1469 Canaries in the coal mine Maeve Barry ORIGINAL ARTICLES COPD 1472 The impact of COPD on health status: findings from the BOLD study Open Christer Janson, Guy Marks, Sonia Buist, Louisa Gnatiuc, Thorarinn Gislason, Mary Ann McBurnie, ERJ Rune Nielsen, Michael Studnicka, Brett Toelle, Bryndis Benediktsdottir and Peter Burney 1484 Dual bronchodilation with QVA149 versus single bronchodilator therapy: the -

6 Chronic Abdominal Pain in Children
6 Chronic Abdominal Pain in Children Chronic Abdominal Pain in Children in Children Pain Abdominal Chronic Chronische buikpijn bij kinderen Carolien Gijsbers Carolien Gijsbers Carolien Chronic Abdominal Pain in Children Chronische buikpijn bij kinderen Carolien Gijsbers Promotiereeks HagaZiekenhuis Het HagaZiekenhuis van Den Haag is trots op medewerkers die fundamentele bijdragen leveren aan de wetenschap en stimuleert hen daartoe. Om die reden biedt het HagaZiekenhuis promovendi de mogelijkheid hun dissertatie te publiceren in een speciale Haga uitgave, die onderdeel is van de promotiereeks van het HagaZiekenhuis. Daarnaast kunnen promovendi in het wetenschapsmagazine HagaScoop van het ziekenhuis aan het woord komen over hun promotieonderzoek. Chronic Abdominal Pain in Children Chronische buikpijn bij kinderen © Carolien Gijsbers 2012 Den Haag ISBN: 978-90-9027270-2 Vormgeving en opmaak De VormCompagnie, Houten Druk DR&DV Media Services, Amsterdam Printing and distribution of this thesis is supported by HagaZiekenhuis. All rights reserved. Subject to the exceptions provided for by law, no part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form by any means, electronic, mechanical, photocopying, recording or otherwise, without the written consent of the author. Chronic Abdominal Pain in Children Chronische buikpijn bij kinderen Carolien Gijsbers Proefschrift ter verkrijging van de graad van doctor aan de Erasmus Universiteit Rotterdam op gezag van de rector magnificus Prof.dr. H.G. Schmidt en volgens besluit van het College voor Promoties. De openbare verdediging zal plaatsvinden op donderdag 20 december 2012 om 15.30 uur door Carolina Francesca Maria Gijsbers geboren te Zierikzee Promotiecommisie Promotor: Prof.dr. H.A.