A Biogeochemical Model of Lake Pusiano (North Italy) and Its Use in the Predictability of Phytoplankton Blooms: First Preliminary Results
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Camera Di Commercio Di COMO-LECCO
Ulisse — InfoCamere Pagina 1 di 56 Camera di Commercio di COMO-LECCO Elenco CO5955433500 del 03/06/2019 11:45:41 Registro Imprese ordinato per [tipo movimento, comune, denominazione] Utente: CCO0096 Posizioni: 258 Note: ISCRITTE Criteri: Impresa - Tipo Solo Imprese nuove iscritte Impresa - Albo Registro Imprese Impresa - Territorio COMO Impresa - Periodo Registrazione dal 01/05/2019 al 31/05/2019. 1) Prov: CO Sezioni RI: O Data iscrizione RI: 21/05/2019 N.REA: 400765 F.G.: SR Denominazione: GDL S.R.L. C.fiscale: 03840770139 Partita IVA: 03840770139 Indirizzo: VIA C. CANTU', 1 Comune: 22031 ALBAVILLA - CO - INATTIVA - Capitale Sociale: deliberato 10.000,00 Valuta capitale sociale: EURO 1) pers.: RUBINO MASSIMO, PRESIDENTE CONSIGLIO AMMINISTRAZIONE, CONSIGLIERE 2) pers.: RODA MAURIZIO FRANCESCO, CONSIGLIERE 2) Prov: CO Sezioni RI: P Data iscrizione RI: 24/05/2019 N.REA: 400812 F.G.: DI Ditta: HU XIANZE C.fiscale: HUXXNZ96L20H501C Partita IVA: 02062370669 Indirizzo: VIA MILANO, 15 Comune: 22031 ALBAVILLA - CO - INATTIVA - Attività: COMMERCIO AL DETTAGLIO DI GENERI DI MONOPOLIO (TABACCHERIE) COMMERCIO AL DETTAGLIO DI GIORNALI, RIVISTE E PERIODICI http://ulisse.intra.infocamere.it/ulis/gestione/get -document -content.action 03/ 06/ 2019 Ulisse — InfoCamere Pagina 2 di 56 1) pers.: HU XIANZE, TITOLARE FIRMATARIO 3) Prov: CO Sezioni RI: P - A Data iscrizione RI: 23/05/2019 N.REA: 400781 F.G.: DI Ditta: POLETTI GIORGIO C.fiscale: PLTGRG71T21C933L Partita IVA: 03838110132 Indirizzo: VIA ROMA, 83 Comune: 22032 ALBESE CON CASSANO - CO Data dom./accert.: 21/05/2019 Data inizio attività: 21/05/2019 Attività: INTONACATURA E TINTEGGIATURA C. Attività: 43.34 I / 43.34 A 1) pers.: POLETTI GIORGIO, TITOLARE FIRMATARIO 4) Prov: CO Sezioni RI: P - C Data iscrizione RI: 07/05/2019 N.REA: 400576 F.G.: DI Ditta: AZIENDA AGRICOLA LOLO DI BOVETTI FRANCESCO C.fiscale: BVTFNC84S01F205Q Partita IVA: 03839240136 Indirizzo: LOCALITA' RONDANINO SN Comune: 22024 ALTA VALLE INTELVI - CO Data inizio attività: 02/05/2019 Attività: ALLEVAMENTO DI EQUINI, COLTIVAZIONI FORAGGERE E SILVICOLTURA. -

C40 Covid Dal 29.04.2021.Xlsx
C_40 - D_41 Como - Erba - Lecco VETTORE ASF FERIALE INVERNALE 6 Corse che si effettuano solo il Sabato. 2 Si effeua solo nei giorni di Vacanze Scolasche Invernali. 3 Si effettua solo il Sabato feriale. 15 Si effettua solo il Sabato scolastico. 49 La corsa proviene da Asso con Linea C 9. 52 La corsa transita da Erba Corso XXV Aprile ed omette la fermata di Erba Stazione. 68 La corsa da Lipomo per Lazzago effettua il percorso: Lora via Oltrecolle - - via Canturina - via P. Paoli - via )iussani - via Varesina - Lazzago Magistri. 89 La corsa prosegue per Asso con linea C 9. C3 Corsa soggetta ad integrazione tariffa urbana per i passeggeri diretti o provenienti a/da Lazzago Magistri C. U/ Corse che non effettuano servizio in ambito urbano a Como. IL SERVIZIO È SOSPESO IL 25 DICEMBRE, IL 1° GENNAIO ED IL 1° MAGGIO seguono quadri orario AREA BRIANZA - INVERNALE 2021/22 C_40 - D_41 Como - Erba - Lecco VETTORE ASF FERIALE INVERNALE 400002 D41002 400008 400014 400028 400032 400050 400034 400036 400038 400052 400022 L41008 400030 400044 400046 400048 Fer6 Fer6 Scol Fer6 Scol Fer6 Scol Scol Sco5 Fer6 Scol Fer6 Scol Sco5 Fer6 Fer6 Fer6 49 2 Lazzago - Magistri Cumacini Como - Stazione Autolinee 05..0 05. 5 06..0 06. 5 00.05 00.01 00.09 Como - P.zza Popolo - Via Dante 05..1 05. 6 06..1 06. 6 00.06 00.09 00.10 Lora - Crotto del Sergente 05. 0 05.55 06. 0 06.55 00.15 00.11 00.19 Lipomo - Bivio Paese - Rondò 05. -

DELIBERAZIONE N° XI / 4882 Seduta Del 14/06/2021
DELIBERAZIONE N° XI / 4882 Seduta del 14/06/2021 Presidente ATTILIO FONTANA Assessori regionali LETIZIA MORATTI Vice Presidente GUIDO GUIDESI STEFANO BOLOGNINI ALESSANDRA LOCATELLI DAVIDE CARLO CAPARINI LARA MAGONI RAFFAELE CATTANEO ALESSANDRO MATTINZOLI RICCARDO DE CORATO FABIO ROLFI MELANIA DE NICHILO RIZZOLI FABRIZIO SALA PIETRO FORONI MASSIMO SERTORI STEFANO BRUNO GALLI CLAUDIA MARIA TERZI Con l'assistenza del Segretario Enrico Gasparini Su proposta dell'Assessore Riccardo De Corato Oggetto SCHEMA DI ACCORDO DI COLLABORAZIONE PER LA REALIZZAZIONE DI INTERVENTI INTEGRATI DI SICUREZZA URBANA DA ATTUARE SUL TERRITORIO DEI COMUNI DI COMO, CANTÙ, CUCCIAGO, CAPIAGO INTIMIANO, ERBA, PUSIANO, EUPILIO, MARIANO COMENSE, COLICO, SAN FERMO DELLA BATTAGLIA, CERNOBBIO, MOLTRASIO, CARATE URIO, LAGLIO, BRIENNO, BLEVIO, TORNO, FAGGETO LARIO, POGNANA LARIO, NESSO, LEZZENO, BELLAGIO, COLICO, DERVIO, DORIO, SUEGLIO E VALVARRONE, DALLA DATA DI SOTTOSCRIZIONE FINO AL 15 NOVEMBRE 2021 Si esprime parere di regolarità amministrativa ai sensi dell'art.4, comma 1, l.r. n.17/2014: Il Direttore Generale Fabrizio Cristalli Il Dirigente Antonino Carrara L'atto si compone di 13 pagine di cui 7 pagine di allegati parte integrante VISTA la legge regionale 1 aprile 2015 n. 6 "Disciplina regionale dei servizi di polizia locale e promozione di politiche integrate di sicurezza urbana" e, in particolare, le seguenti disposizioni, che prevedono: - art. 1, comma 3: il coordinamento tra i servizi di polizia locale, in armonia con la normativa quadro in materia di polizia locale e nel rispetto dell’autonomia organizzativa dell’ente locale da cui dipende il personale, per l’erogazione di servizi più efficaci ed efficienti a vantaggio del territorio e della cittadinanza; - art. -

Elenco Comuni Fascia 2 Totale
ELENCO COMUNI FASCIA 2 TOTALE : 361 COMUNI Provincia di Milano (69 Comuni) Provincia Comune MI NOSATE MI ABBIATEGRASSO MI OSSONA MI ALBAIRATE MI PANTIGLIATE MI ARCONATE MI PESSANO CON BORNAGO MI ARLUNO MI PIEVE EMANUELE MI BAREGGIO MI POZZO D'ADDA MI BASIANO MI POZZUOLO MARTESANA MI BASIGLIO MI PREGNANA MILANESE MI BELLINZAGO LOMBARDO MI ROBECCHETTO CON INDUNO MI BERNATE TICINO MI ROBECCO SUL NAVIGLIO MI BOFFALORA SOPRA TICINO MI RODANO MI BUSCATE MI SAN GIULIANO MILANESE MI BUSSERO MI SANTO STEFANO TICINO MI BUSTO GAROLFO MI SEDRIANO MI CAMBIAGO MI SETTALA MI CASOREZZO MI SOLARO MI CASSANO D'ADDA MI TREZZANO ROSA MI CASSINA DE' PECCHI MI TREZZANO SUL NAVIGLIO MI CASSINETTA DI LUGAGNANO MI TREZZO SULL'ADDA MI CASTANO PRIMO MI TRUCCAZZANO MI CISLIANO MI TURBIGO MI CORBETTA MI VANZAGHELLO MI CORNAREDO MI VANZAGO MI CUGGIONO MI VAPRIO D'ADDA MI CUSAGO MI VERMEZZO MI DAIRAGO MI VIGNATE MI GAGGIANO MI VILLA CORTESE MI GESSATE MI VITTUONE MI GORGONZOLA MI ZIBIDO SAN GIACOMO MI GREZZAGO MI INVERUNO MI INZAGO Provincia di Bergamo (74 Comuni) MI LISCATE Provincia Comune MI LOCATE TRIULZI BG ALBINO MI MAGENTA BG AMBIVERE MI MAGNAGO BG ARZAGO D'ADDA MI MARCALLO CON CASONE BG BAGNATICA MI MASATE BG BARIANO MI MEDIGLIA BG BOLGARE MI MELZO BG BONATE SOPRA MI MESERO BG BONATE SOTTO BG PALAZZAGO BG BOTTANUCO BG PALOSCO BG BREMBATE DI SOPRA BG POGNANO BG BRIGNANO GERA D'ADDA BG PONTIDA BG CALCINATE BG PRADALUNGA BG CALCIO BG PRESEZZO BG CALUSCO D'ADDA BG ROMANO DI LOMBARDIA BG CALVENZANO BG SOLZA BG CAPRIATE SAN GERVASO BG SORISOLE BG CAPRINO BERGAMASCO -

Adi Merone – Ente Gestore Cooperativa Sociale Quadrifoglio S.C
ENTI EROGATORI ADI Distretto Brianza • PAXME ASSISTANCE • ALE.MAR. COOPERATIVA SOCIALE ONLUS Como (CO) Via Castelnuovo, 1 Vigevano (PV) Via SS. Crispino e Crispiniano, 2 Tel. 031.4490272 / 340.2323524 Tel. 0381/73703 – fax 0381/76908 e-mail: [email protected] e-mail: [email protected] Anche cure palliative • PUNTO SERVICE C/O RSA Croce di Malta • ASSOCIAZIONE A.QU.A. ONLUS Canzo (CO) Via Brusa, 20 Milano (MI) Via Panale, 66 Tel. 346.2314311 - fax 031.681787 Tel. 02.36552585 - fax 02.36551907 e-mail: [email protected] e-mail: [email protected] • SAN CAMILLO - PROGETTO ASSISTENZA s.r.l. • ASSOCIAZIONE ÀNCORA Varese (VA) Via Lungolago di Calcinate, 88 Longone al Segrino (CO) Via Diaz, 4 Tel. 0332.264820 - fax 0332.341682 Tel/fax 031.3357127 e-mail: [email protected] e-mail: [email protected] Anche cure palliative Solo cure palliative • VIVISOL Solo per i Comuni di: Albavilla, Alserio, Alzate Sesto San Giovanni (MI) Via Manin, 167 Brianza, Anzano del Parco, Asso, Barni, Caglio, Tel. 800.990.161 – fax 02.26223985 Canzo, Caslino d’Erba, Castelmarte, Civenna, e-mail: [email protected] Erba, Eupilio, Lambrugo, Lasnigo, Longone al Anche cure palliative Segrino, Magreglio, Merone, Monguzzo,Orsenigo, Ponte Lambro, Proserpio, Pusiano, Rezzago, Sormano, Valbrona. • ATHENA CENTRO MEDICO Ferno (VA) Via De Gasperi, 1 Tel. 0331.726361 – Fax 0331.728270 e-mail: [email protected] Anche cure palliative • ADI MERONE – ENTE GESTORE COOPERATIVA SOCIALE QUADRIFOGLIO S.C. ONLUS Merone (CO) Via Leopardi, 5/1 Tel 031.651781 - 329.2318205 -

Formato Europeo Per Il Curriculum Vitae
CURRICULUM VITAE INFORMAZIONI PERSONALI Nome ANTONIA GIOVANNA COLOMBO Indirizzo Via G. Ungaretti 3 – MERONE - CO Nazionalità Italiana Data di nascita 27.04.1960 ESPERIENZE LAVORATIVE • Date (da – a) 01.05.1980 ad oggi • Nome e indirizzo del Comune di Monguzzo, Via Santuario, 11, Monguzzo datore di lavoro • Tipo di azienda o settore Ente locale • Tipo di impiego Tempo pieno – a tempo indeterminato Responsabile servizio finanziario-tributi • Principali mansioni e Gestione e coordinamento della contabilità finanziaria, economica responsabilità patrimoniale dell’Ente. Predisposizione degli atti di programmazione economico-finanziaria: bilancio di previsione- rendiconto di gestione- relazione Corte dei conti e di tutti gli atti connessi e conseguenti alla gestione dei suddetti strumenti di programmazione. Tenuta sistematica delle rilevazioni contabili riguardanti le entrate e spese nelle varie fasi e gestione degli adempimenti connessi compresi i rapporti con la Tesoreria Comunale. Corresponsione del trattamento economico ai dipendenti, adempimenti contabili ad esso correlati. Adempimenti fiscali. Gestione tributi comunali: parte economica e trasmissione dati e certificazioni relativi ai tributi ed ai servizi a rilevanza economica. Predisposizione regolamenti, delibere e determinazioni inerenti l’area economica e tributaria • Date (da – a) 1.05.2008 al 31.07.2009 • Nome e indirizzo del Comune di Colle Brianza, Piazza Roma, Colle Brianza datore di lavoro • Tipo di azienda o settore Ente locale • Tipo di impiego Incarico di collaborazione a -

4 DEF Regolamentopesca 148X210+5Abb ING
FISHING AND NAVIGATION ON LAKE PUSIANO FFISHINGISHING RREGULATIONSEGULATIONS www.lagopusiano.com RECREATIONAL FISHING RULES FISHING RULES IN THE WATERS OF LAKE PUSIANO ON LAKE PUSIANO PREMISE Egirent Services srl, owner of the Fishing and Navigation Rights on Lake Pusiano, operates WHAT IS REQUIRED TO FISH ON LAKE PUSIANO? on Lake Pusiano with the mission of making this enchanting lake basin an authentic paradise for The fi sherman must be in possession of a valid Italian fi shing license, a catch record card issued local, Italian and international fi shermen. Egirent Services Srl makes transparency and by the Lombardy Region Authority (valid for the current year) and of a valid fi shing permit for lake dialogue the cornerstones of its activity and works at 360 degrees for the promotion of Lake Pusiano issued by the Egirent Services society at the Info Point of Pusiano (CO), 30 Pusiano. via Mazzini. Foreign citizens, too, must be in possession of a Goverment Licence, a catch record For these reasons, Egirent Services srl reserves the right not to grant the fi shing permit card and a valid fi shing permit for Lake Pusiano. All fi shing activities on Lake Pusian shall only be to those who, at their own discretion, have bad behaviors or cause moral and image damage to allowed if they are in complaince with Egirent Services Fishing Regulations as well as Lake Pusiano. Similarly, Egirent Services srl will have the right to cancel permits already with national, regional and provincial rules. issued to those fi shermen who demonstrate disagreement with the corporate philosophy of the The payment form for the government licence is available at the Egirent Services Info protection and care of the Lake. -
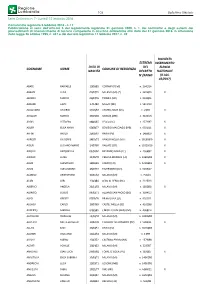
Cognome Nome Data Di Nascita Comune Di Residenza
– 108 – Bollettino Ufficiale Serie Ordinaria n. 7 - Lunedì 12 febbraio 2018 Comunicato regionale 5 febbraio 2018 - n. 17 Pubblicazione ai sensi dell’articolo 5 del regolamento regionale 21 gennaio 2000, n. 1, dei nominativi e degli estremi dei provvedimenti di riconoscimento di tecnico competente in acustica ambientale alla data del 31 gennaio 2018, in attuazione della legge 26 ottobre 1995, n. 447 e del decreto legislativo 17 febbraio 2017, n. 42 RICHIESTA ESTREMI INSERIMENTO DATA DI DEL ELENCO COGNOME NOME COMUNE DI RESIDENZA NASCITA DECRETO NAZIONALE N°/ANNO (D.LGS. 42/2017) ABATE RAFFAELE 13/08/85 CORMANO (MI) n. 2641/14 ABBATE LUCA 0 5/07/7 9 MILANO (MI) (*) n. 3824/09 X ABORDI MARCO 0 6/0 7/7 6 TIRANO (SO) n. 9325/05 ABRAMI LAPO 2 7/0 7/8 0 MELZO (MI) n. 5874/10 ACQUADRO VALERIO 17/10/67 CASTELLANZA (VA) n. 2 7/0 3 X ACQUATI MARCO 28/05/68 MONZA (MB) n. 3224/13 ADDIS VITTORIO 08/06/45 LECCO (LC) n. 2571/97 X ADLER ELISA ANNA 03/08/77 BOVISIO MASCIAGO (MB) n. 9921/11 X AFFINI PAOLO 2 5/0 9 /67 PAVIA (PV) n. 1486/00 X AGRESTI GIUSEPPE 24/09/72 VANZAGHELLO (VA) n. 18189/00 X AIOLFI LUCIANO MARIO 1 4/07/6 0 VAILATE (CR) n. 11059/16 X AIROLDI ANTONELLA 0 9 /0 2/6 2 PADERNO ADDA (LC) n. 2566/97 X AIROLDI LUISA 10/05/70 CESANA BRIANZA (LC) n. 13655/08 X AJANI GIAMPIERO 28/06/49 COMO (CO) n. -

COMUNE DI EUPILIO Provincia Di Como
COMUNE DI EUPILIO Provincia di Como PIANO DI GOVERNO DEL TERRITORIO Legge Regionale 12/2005 DOCUMENTO DI PIANO RELAZIONE (Aprile 2011 – Agg. Giugno 2012) Dott. Arch. Giacomino Amadeo Dott. Arch. Arnaldo Falbo Ordine Architetti PPC di Monza e Brianza n. 2622 Ordine Architetti PPC di Como n. 1483 Via S. Carlo, 1 - 20811 Cesano Maderno (MB) Via Ballerini, 12 - 22100 Como (CO) Tel. +39 0362 500200 - Fax +39 0362 1580711 Tel. +39 031 241646 - Fax +39 031 4129304 [email protected] [email protected] INDICE PARTE I Sezione I - Quadro conoscitivo 1. - Luogo, paesaggi e ambienti 1.1 - Luogo storia e territorio 1.2 - Il paesaggio locale 1.3 - La struttura del paesaggio agrario 1.3.1 - Quadro conoscitivo 1.4 - Ambienti urbani e morfologia dell’edificato 1.5 - Indagini specialistiche 1.5.1 - Studio geologico e idrogeologico 1.5.2 - Definizione del reticolo idrografico minore 1.5.3 - Azzonamento acustico 2. - L’assetto infrastrutturale 2.1 - La viabilità 2.2 - Il trasporto pubblico 2.3 - I percorsi ciclabili – la Ciclovia dei Laghi 2.4 - La rete fognaria esistente 3. - L’ambiente costruito 3.1 - Il patrimonio edificato 3.2 - Il patrimonio paesaggistico e ambientale 4. - Servizi e attrezzature - pubblici e di uso pubblico 4.1 - Servizi e attrezzature pubblici 5. - Analisi demografica e socioeconomica 5.1 - Struttura e dinamica della popolazione Sezione II - Quadro ricognitivo di riferimento a) Piano Territoriale Regionale (PTR) b) Piano Territoriale di Coordinamento Provinciale (PTCP) c) Parco della Valle del Lambro d) Parco Locale di Interesse Sovracomunale del Lago del Segrino e) Piano di gestione Sito di Importanza Comunitaria del Lago di Pusiano -(IT2020006) f) Piano di gestione Sito di Importanza Comunitaria del Lago del Segrino - (IT2020010) g) Piano di indirizzo Forestale della Comunità Montana del Triangolo Lariano h) Le proposte e segnalazioni dei cittadini EUPILIO-REL-DP-DEF-REV-01 - Pagina - 2 - di 141 PARTE II - Obiettivi di intervento e strategie attuative 6. -

TOURIST GUIDE ASSOCIATIONS PROVINCE of COMO Associazione Guide E Accompagnatori Turistici Di Como E Provincia Phone No
TOURIST GUIDE www.lakecomo.com ISOLA COMACINA 01_ING_presen_sistema.indd 1 25/07/11 11:40 PRESENTATION This Tourist Guide introduces one of the most beautiful areas in the region called Lombardy and enthusiastically welcomes all visitors who are planning to have an enjoyable stay here. Seen from above, the blue of the lakes and the green of the woods are the two colours which exist in harmony in this spectacular landscape full of panoramas. The lakes are the main characteristic of Como and Lecco provinces, surrounded by a range of important mountains which open up to the hilly countryside of Brianza to the South, the home to entrepreneurship. We had the idea of preparing a guide that was not only easy to use, but of high quality: therefore, you will fi nd, alongside the usual cultural itineraries that inform you of our national heritage, practical information that can help you to easily discover our region and even the less known Via Sirtori 5 - 22100 Como places. Phone No. + 39 031 2755551 Subdivided into geographical areas of lake, mountain Fax + 39 031 2755569 and plain, the Guide describes the entire territory of [email protected] www.provincia.como.it Como and Lecco provinces; its history, architecture, art www.lakecomo.com and natural beauty, starting from the “capoluoghi” (main towns) of the province and the lake basin. It then goes on describing the mountain area and cultural features, uncovering the towns and ancient villages, alongside the mountain shelters and peaks. It gives detailed information on walking excursions for all nature lovers, from trekking to all types of sport. -

Como Cantù Erba
Sorico Dubino LIVO Gera Lario C18 SONDRIO Dosso del Liro Peglio C19 Consiglio Domaso di Rumo Gravedona Stazzona COLICO Morbegno C17 C10 GARZENO C18 Villatico C17 DONGO Capolinea Trieste Lungolario Musso Como Stazione Autolinee Via Torno PIANELLO Dorio C10 C45 C62 DEL LARIO CARVAGNA C19 C20 C46 C60 C14 San Nazzaro San Bartolomeo Cremia C40 C47 C50 Cusino C27 Buggiolo Via Borgovico Stazione Lungolario Trieste Via Manzoni VAL REZZO Piazza Roma Como Lago San Siro Via Sinigaglia Lungolario Trento Via Bianchi Giovini Via Fratelli Rosselli Acquaseria Via Fratelli Cairoli Corrido PLESIO Carlazzo Recchi Fratelli Via Via Dante Alighieri Viale Felice Cavallotti Gottro C13 Viale Masia San Pietro Begna Piano Calveseglio Via Caio Plinio Naggio Ligomena Via Nino Bixio Dasio C27 Logo Tavordo La Santa Barna Capolinea Loveno Nobiallo C22 PORLEZZA Stazione Via Borgovico Viale Lecco Bene Lario San Mamete Cima Cardano S. Giovanni Capolinea Capolinea Capolinea Albogasio Cressogno Grandola Piazza Stazione Piazza del Oria MENAGGIO C30 C31 Via Tolomeo Gallio Cavour Lago Popolo Croce C10 C12 C32 C70 C43 C49 C52 Viale Varese C12 Gandria Osteno Viale Innocenzo XI LUGANO C13 Lago di C74 Claino C14 Como Ramponio Verna Griante C71 C23 Cadenabbia Scaria BELLAGIO Ramponio PONNA Laino Tremezzo Mezzegra C30 C20 Pellio Intelvi LANZO INTELVI C36 Capolinea Lenno C22 C23 C24 Visgnola Stazione Erba Ossuccio Erba SAN FEDELE Via Adua Sala Via Leopardi C40 C90 C94 Comacina Via Massimo d’Azeglio Via Ferraris Blessagno PIGRA Colonno C49 C91 C95 Via XXV Aprile Castiglione C24 Guello -

2012 361 Comuni Ex Area Critica A2
Da sito della Regione: http://www.regione.lombardia.it/cs/Satellite?c=News&cid=1213556215052&childpagename=Regione%2FDet ail&pagename=RGNWrapper (Ln - Milano) Di seguito l'elenco dei 361 ai quali potrebbe essere esteso il fermo dei mezzi più inquinanti. PROVINCIA DI MILANO : 69 Comuni - Abbiategrasso, Albairate, Arconate, Arluno, Bareggio, Basiano, Basiglio, Bellinzago Lombardo, Bernate Ticino, Boffalora Sopra Ticino, Buscate, Bussero, Busto Garolfo, Cambiago, Casorezzo, Cassano d'Adda, Cassina De' Pecchi, Cassinetta di Lugagnano, Castano Primo, Cisliano, Corbetta, Cornaredo, Cuggiono, Cusago, Dairago, Gaggiano, Gessate, Gorgonzola, Grezzago, Inveruno, Inzago, Liscate, Locate Triulzi, Magenta, Magnago, Marcallo Con Casone, Masate, Mediglia, Melzo, Mesero, Nosate, Ossona, Pantigliate, Pessano Con Bornago, Pieve Emanuele, Pozzo d'Adda, Pozzuolo Martesana, Pregnana Milanese, Robecchetto con Induno, Robecco sul Naviglio, Rodano, San Giuliano Milanese, Santo Stefano Ticino, Sedriano, Settala, Solaro, Trezzano Rosa, Trezzano sul Naviglio, Trezzo sull'Adda, Truccazzano, Turbigo, Vanzaghello, Vanzago, Vaprio d'Adda, Vermezzo, Vignate, Villa Cortese, Vittuone, Zibido San Giacomo. PROVINCIA DI BERGAMO : 74 Comuni - Albino, Ambivere, Arzago d'Adda, Bagnatica, Bariano, Barzana, Bolgare, Bonate Sopra, Bonate Sotto, Bottanuco, Brembate di Sopra, Brignano Gera d'Adda, Calcinate, Calcio, Calusco d'Adda, Calvenzano, Capriate San Gervaso, Caprino Bergamasco, Caravaggio, Carvico, Casirate d'Adda, Castel Rozzone, Castelli Calepio, Cavernago, Cenate Sopra,