CHAPTER 3 Comparing Disease Frequencies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Descriptive Statistics (Part 2): Interpreting Study Results
Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk. -

Meta-Analysis of Proportions
NCSS Statistical Software NCSS.com Chapter 456 Meta-Analysis of Proportions Introduction This module performs a meta-analysis of a set of two-group, binary-event studies. These studies have a treatment group (arm) and a control group. The results of each study may be summarized as counts in a 2-by-2 table. The program provides a complete set of numeric reports and plots to allow the investigation and presentation of the studies. The plots include the forest plot, radial plot, and L’Abbe plot. Both fixed-, and random-, effects models are available for analysis. Meta-Analysis refers to methods for the systematic review of a set of individual studies with the aim to combine their results. Meta-analysis has become popular for a number of reasons: 1. The adoption of evidence-based medicine which requires that all reliable information is considered. 2. The desire to avoid narrative reviews which are often misleading. 3. The desire to interpret the large number of studies that may have been conducted about a specific treatment. 4. The desire to increase the statistical power of the results be combining many small-size studies. The goals of meta-analysis may be summarized as follows. A meta-analysis seeks to systematically review all pertinent evidence, provide quantitative summaries, integrate results across studies, and provide an overall interpretation of these studies. We have found many books and articles on meta-analysis. In this chapter, we briefly summarize the information in Sutton et al (2000) and Thompson (1998). Refer to those sources for more details about how to conduct a meta- analysis. -
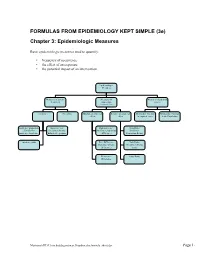
FORMULAS from EPIDEMIOLOGY KEPT SIMPLE (3E) Chapter 3: Epidemiologic Measures
FORMULAS FROM EPIDEMIOLOGY KEPT SIMPLE (3e) Chapter 3: Epidemiologic Measures Basic epidemiologic measures used to quantify: • frequency of occurrence • the effect of an exposure • the potential impact of an intervention. Epidemiologic Measures Measures of disease Measures of Measures of potential frequency association impact (“Measures of Effect”) Incidence Prevalence Absolute measures of Relative measures of Attributable Fraction Attributable Fraction effect effect in exposed cases in the Population Incidence proportion Incidence rate Risk difference Risk Ratio (Cumulative (incidence density, (Incidence proportion (Incidence Incidence, Incidence hazard rate, person- difference) Proportion Ratio) Risk) time rate) Incidence odds Rate Difference Rate Ratio (Incidence density (Incidence density difference) ratio) Prevalence Odds Ratio Difference Macintosh HD:Users:buddygerstman:Dropbox:eks:formula_sheet.doc Page 1 of 7 3.1 Measures of Disease Frequency No. of onsets Incidence Proportion = No. at risk at beginning of follow-up • Also called risk, average risk, and cumulative incidence. • Can be measured in cohorts (closed populations) only. • Requires follow-up of individuals. No. of onsets Incidence Rate = ∑person-time • Also called incidence density and average hazard. • When disease is rare (incidence proportion < 5%), incidence rate ≈ incidence proportion. • In cohorts (closed populations), it is best to sum individual person-time longitudinally. It can also be estimated as Σperson-time ≈ (average population size) × (duration of follow-up). Actuarial adjustments may be needed when the disease outcome is not rare. • In an open populations, Σperson-time ≈ (average population size) × (duration of follow-up). Examples of incidence rates in open populations include: births Crude birth rate (per m) = × m mid-year population size deaths Crude mortality rate (per m) = × m mid-year population size deaths < 1 year of age Infant mortality rate (per m) = × m live births No. -

Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple As It Can Get Chittaranjan Andrade, MD
Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple as It Can Get Chittaranjan Andrade, MD Each month in his online Introduction column, Dr Andrade Many research papers present findings as odds ratios (ORs) and considers theoretical and relative risks (RRs) as measures of effect size for categorical outcomes. practical ideas in clinical Whereas these and related terms have been well explained in many psychopharmacology articles,1–5 this article presents a version, with examples, that is meant with a view to update the knowledge and skills to be both simple and practical. Readers may note that the explanations of medical practitioners and examples provided apply mostly to randomized controlled trials who treat patients with (RCTs), cohort studies, and case-control studies. Nevertheless, similar psychiatric conditions. principles operate when these concepts are applied in epidemiologic Department of Psychopharmacology, National Institute research. Whereas the terms may be applied slightly differently in of Mental Health and Neurosciences, Bangalore, India different explanatory texts, the general principles are the same. ([email protected]). ABSTRACT Clinical Situation Risk, and related measures of effect size (for Consider a hypothetical RCT in which 76 depressed patients were categorical outcomes) such as relative risks and randomly assigned to receive either venlafaxine (n = 40) or placebo odds ratios, are frequently presented in research (n = 36) for 8 weeks. During the trial, new-onset sexual dysfunction articles. Not all readers know how these statistics was identified in 8 patients treated with venlafaxine and in 3 patients are derived and interpreted, nor are all readers treated with placebo. These results are presented in Table 1. -

Outcome Reporting Bias in COVID-19 Mrna Vaccine Clinical Trials
medicina Perspective Outcome Reporting Bias in COVID-19 mRNA Vaccine Clinical Trials Ronald B. Brown School of Public Health and Health Systems, University of Waterloo, Waterloo, ON N2L3G1, Canada; [email protected] Abstract: Relative risk reduction and absolute risk reduction measures in the evaluation of clinical trial data are poorly understood by health professionals and the public. The absence of reported absolute risk reduction in COVID-19 vaccine clinical trials can lead to outcome reporting bias that affects the interpretation of vaccine efficacy. The present article uses clinical epidemiologic tools to critically appraise reports of efficacy in Pfzier/BioNTech and Moderna COVID-19 mRNA vaccine clinical trials. Based on data reported by the manufacturer for Pfzier/BioNTech vaccine BNT162b2, this critical appraisal shows: relative risk reduction, 95.1%; 95% CI, 90.0% to 97.6%; p = 0.016; absolute risk reduction, 0.7%; 95% CI, 0.59% to 0.83%; p < 0.000. For the Moderna vaccine mRNA-1273, the appraisal shows: relative risk reduction, 94.1%; 95% CI, 89.1% to 96.8%; p = 0.004; absolute risk reduction, 1.1%; 95% CI, 0.97% to 1.32%; p < 0.000. Unreported absolute risk reduction measures of 0.7% and 1.1% for the Pfzier/BioNTech and Moderna vaccines, respectively, are very much lower than the reported relative risk reduction measures. Reporting absolute risk reduction measures is essential to prevent outcome reporting bias in evaluation of COVID-19 vaccine efficacy. Keywords: mRNA vaccine; COVID-19 vaccine; vaccine efficacy; relative risk reduction; absolute risk reduction; number needed to vaccinate; outcome reporting bias; clinical epidemiology; critical appraisal; evidence-based medicine Citation: Brown, R.B. -

Copyright 2009, the Johns Hopkins University and John Mcgready. All Rights Reserved
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this site. Copyright 2009, The Johns Hopkins University and John McGready. All rights reserved. Use of these materials permitted only in accordance with license rights granted. Materials provided “AS IS”; no representations or warranties provided. User assumes all responsibility for use, and all liability related thereto, and must independently review all materials for accuracy and efficacy. May contain materials owned by others. User is responsible for obtaining permissions for use from third parties as needed. Section F Measures of Association: Risk Difference, Relative Risk, and the Odds Ratio Risk Difference Risk difference (attributable risk)—difference in proportions - Sample (estimated) risk difference - Example: the difference in risk of HIV for children born to HIV+ mothers taking AZT relative to HIV+ mothers taking placebo 3 Risk Difference From csi command, with 95% CI 4 Risk Difference Interpretation, sample estimate - If AZT was given to 1,000 HIV infected pregnant women, this would reduce the number of HIV positive infants by 150 (relative to the number of HIV positive infants born to 1,000 women not treated with AZT) Interpretation 95% CI - Study results suggest that the reduction in HIV positive births from 1,000 HIV positive pregnant women treated with AZT could range from 75 to 220 fewer than the number occurring if the -

Clinical Epidemiologic Definations
CLINICAL EPIDEMIOLOGIC DEFINATIONS 1. STUDY DESIGN Case-series: Report of a number of cases of disease. Cross-sectional study: Study design, concurrently measure outcome (disease) and risk factor. Compare proportion of diseased group with risk factor, with proportion of non-diseased group with risk factor. Case-control study: Retrospective comparison of exposures of persons with disease (cases) with those of persons without the disease (controls) (see Retrospective study). Retrospective study: Study design in which cases where individuals who had an outcome event in question are collected and analyzed after the outcomes have occurred (see also Case-control study). Cohort study: Follow-up of exposed and non-exposed defined groups, with a comparison of disease rates during the time covered. Prospective study: Study design where one or more groups (cohorts) of individuals who have not yet had the outcome event in question are monitored for the number of such events, which occur over time. Randomized controlled trial: Study design where treatments, interventions, or enrollment into different study groups are assigned by random allocation rather than by conscious decisions of clinicians or patients. If the sample size is large enough, this study design avoids problems of bias and confounding variables by assuring that both known and unknown determinants of outcome are evenly distributed between treatment and control groups. Bias (Syn: systematic error): Deviation of results or inferences from the truth, or processes leading to such deviation. See also Referral Bias, Selection Bias. Recall bias: Systematic error due to the differences in accuracy or completeness of recall to memory of past events or experiences. -

Making Comparisons
Making comparisons • Previous sessions looked at how to describe a single group of subjects • However, we are often interested in comparing two groups Data can be interpreted using the following fundamental questions: • Is there a difference? Examine the effect size • How big is it? • What are the implications of conducting the study on a sample of people (confidence interval) • Is the effect real? Could the observed effect size be a chance finding in this particular study? (p-values or statistical significance) • Are the results clinically important? 1 Effect size • A single quantitative summary measure used to interpret research data, and communicate the results more easily • It is obtained by comparing an outcome measure between two or more groups of people (or other object) • Types of effect sizes, and how they are analysed, depend on the type of outcome measure used: – Counting people (i.e. categorical data) – Taking measurements on people (i.e. continuous data) – Time-to-event data Example Aim: • Is Ventolin effective in treating asthma? Design: • Randomised clinical trial • 100 micrograms vs placebo, both delivered by an inhaler Outcome measures: • Whether patients had a severe exacerbation or not • Number of episode-free days per patient (defined as days with no symptoms and no use of rescue medication during one year) 2 Main results proportion of patients Mean No. of episode- No. of Treatment group with severe free days during the patients exacerbation year GROUP A 210 0.30 (63/210) 187 Ventolin GROUP B placebo 213 0.40 (85/213) -

Measures of Effect & Potential Impact
Measures of Effect & Potential Impact Madhukar Pai, MD, PhD Assistant Professor McGill University, Montreal, Canada [email protected] 1 Big Picture Measures of Measures of Measures of potential disease freq effect impact First, we calculate measure of disease frequency in Group 1 vs. Group 2 (e.g. exposed vs. unexposed; treatment vs. placebo, etc.) Then we calculate measures of effect (which aims to quantify the strength of the association): Either as a ratio or as a difference: Ratio = (Measure of disease, group 1) / (Measure of disease, group 2) Difference = (Measure of disease, group 1) - (Measure of disease, group 2) Lastly, we calculate measures of impact, to address the question: if we removed or reduced the exposure, then how much of the disease burden can we reduce? Impact of exposure removal in the exposed group (AR, AR%) Impact of exposure remove in the entire population (PAR, PAR%) 2 Note: there is some overlap between measures of effect and impact 3 Measures of effect: standard 2 x 2 contingency epi table for count data (cohort or case-control or RCT or cross-sectional) Disease - Disease - no Column yes total (Margins) Exposure - a b a+b yes Exposure - c d c+d no Row total a+c b+d a+b+c+d (Margins) 4 Measures of effect: 2 x 2 contingency table for a cohort study or RCT with person-time data Disease - Disease - Total yes no Exposure - a - PYe yes Exposure – c - PY0 no Total a+c - PYe + PY0 Person-time in the unexposed group = PY0 5 Person-time in the exposed group = PYe STATA format for a 2x2 table [note that exposure -

SUPPLEMENTARY APPENDIX Powering Bias and Clinically
SUPPLEMENTARY APPENDIX Powering bias and clinically important treatment effects in randomized trials of critical illness Darryl Abrams, MD, Sydney B. Montesi, MD, Sarah K. L. Moore, MD, Daniel K. Manson, MD, Kaitlin M. Klipper, MD, Meredith A. Case, MD, MBE, Daniel Brodie, MD, Jeremy R. Beitler, MD, MPH Supplementary Appendix 1 Table of Contents Content Page 1. Additional Methods 3 2. Additional Results 4 3. Supplemental Tables a. Table S1. Sample size by trial type 6 b. Table S2. Accuracy of control group mortality by trial type 6 c. Table S3. Predicted absolute risk reduction in mortality by trial type 6 d. Table S4. Difference in predicted verses observed treatment effect, absolute risk difference 6 e. Table S5. Characteristics of trials by government funding 6 f. Table S6. Proportion of trials for which effect estimate includes specified treatment effect size, 7 all trials g. Table S7. Inconclusiveness of important effect size for reduction in mortality among trials 7 without a statistically significant treatment benefit h. Table S8. Inconclusiveness of important effect size for increase in mortality among trials 7 without a statistically significant treatment harm 4. Supplemental Figures a. Figure S1. Screening and inclusion of potentially eligible studies 8 b. Figure S2. Butterfly plot of predicted and observed mortality risk difference, grouped by 9 journal c. Figure S3. Butterfly plot of predicted and observed mortality risk difference, grouped by 10 disease area d. Figure S4. Trial results according to clinically important difference in mortality on absolute 11 and relative scales, grouped by journal e. Figure S5. Trial results according to clinically important difference in mortality on absolute 12 and relative scales, grouped by disease area f. -

Relative Risk Reduction (RRR): Difference Between the Event Rates in Relative Terms: 20% RD/CER - 10%/40% = 25%
Crunching the Numbers Baseline risk and effect on treatment decisions Prof C Heneghan That means in a large clinical study, 3% of patients taking a sugar pill or placebo had a heart attack compared to 2% of patients taking Lipitor. Trial 1: High Risk Patients 40% Control New drug for AMI to reduce mortality 30% First studied in a high risk 20% population: 40% mortality at 30 days among 10% untreated 30% mortality among treated 0% Trial 1: High Risk Patients How would you describe effect of new intervention? Trial 1: High Risk Patients 40% - Risk Difference (RD): 40%-30% = 10% 30% / Relative Risk Reduction (RRR): difference between the event rates in relative terms: 20% RD/CER - 10%/40% = 25% The 10% Risk Difference is expressed as a 10% proportion of the control event rate 0% Trial 1: High Risk Patients Trial 2: Low Risk Patients 40% Control Trial 2: younger patients Intervention New drug for AMI to reduce mortality 30% Later studied in low risk population: 20% 10% mortality at 30 days among untreated 7.5% mortality among treated 10% 0% Trial 1: High risk Trial 2: Low risk How would you describe effect of new intervention? Trial 2: Low Risk Patients 40% Control / Relative Risk Reduction (RRR): difference between the event rates in relative terms: Intervention RD/CER - 2.5%/10% = 25% 30% The 2.5% Risk Difference is expressed as a proportion of the control event rate 20% 10% - Risk Difference (RD): 10%-7.5% = 2.5% 0% Trial 1: High risk Trial 2: Low risk Summary Points for Relative Risk Reduction and Risk Difference • Relative risk reduction is often more impressive than absolute risk reduction. -

Antibiotic Resistance Threats in the United States, 2019
ANTIBIOTIC RESISTANCE THREATS IN THE UNITED STATES 2019 Revised Dec. 2019 This report is dedicated to the 48,700 families who lose a loved one each year to antibiotic resistance or Clostridioides difficile, and the countless healthcare providers, public health experts, innovators, and others who are fighting back with everything they have. Antibiotic Resistance Threats in the United States, 2019 (2019 AR Threats Report) is a publication of the Antibiotic Resistance Coordination and Strategy Unit within the Division of Healthcare Quality Promotion, National Center for Emerging and Zoonotic Infectious Diseases, Centers for Disease Control and Prevention. Suggested citation: CDC. Antibiotic Resistance Threats in the United States, 2019. Atlanta, GA: U.S. Department of Health and Human Services, CDC; 2019. Available online: The full 2019 AR Threats Report, including methods and appendices, is available online at www.cdc.gov/DrugResistance/Biggest-Threats.html. DOI: http://dx.doi.org/10.15620/cdc:82532. ii U.S. Centers for Disease Control and Prevention Contents FOREWORD .............................................................................................................................................V EXECUTIVE SUMMARY ........................................................................................................................ VII SECTION 1: THE THREAT OF ANTIBIOTIC RESISTANCE ....................................................................1 Introduction .................................................................................................................................................................3