DOCSLIB.ORG

Estimating Causal Effects

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Estimating Causal Effects 422_990019 8/4/2002 4:01 pm Page 422 (Black plate) © International Epidemiological Association 2002 Printed in Great Britain International Journal of Epidemiology 2002;31:422–429 THEORY AND METHODS Estimating causal effects George Maldonadoa and Sander Greenlandb Although one goal of aetiologic epidemiology is to estimate ‘the Creator: So you want a descriptive incidence proportion ratio? true effect’ of an exposure on disease occurrence, epidemio- You: No, not descriptive. Causal. An incidence proportion ratio logists usually do not precisely specify what ‘true effect’ they that isolates the effect of E on D from all other causal factors. want to estimate. We describe how the counterfactual theory of causation, originally developed in philosophy and statistics, can Creator: By ‘isolate’, you mean a measure that applies to a be adapted to epidemiological studies to provide precise answers single population under different possible exposure scenarios? to the questions ‘What is a cause?’, ‘How should we measure You: Yes, that’s what I mean. effects?’ and ‘What effect measure should epidemiologists estimate in aetiologic studies?’ We also show that the theory of Creator: OK. Which causal incidence proportion ratio? counterfactuals (1) provides a general framework for designing You: Pardon? and analysing aetiologic studies; (2) shows that we must always depend on a substitution step when estimating effects, and Creator: For what population, and for what time period? The therefore the validity of our estimate will always depend on the true value of a causal incidence proportion ratio can be different validity of the substitution; (3) leads to precise definitions of for different groups of people and for different time periods. It’s effect measure, confounding, confounder, and effect-measure not necessarily a biological constant, you know. modification; and (4) shows why effect measures should be You: Yes, of course. For population (your population here, expected to vary across populations whenever the distribution denoted by P) between the years (your study time period here, of causal factors varies across the populations. denoted by t0 to t1). Creator: By population P, do you mean: (1) everyone in popu- Introduction lation P, or (2) the people in population P who have a specific Imagine that the creator of the universe appears to you in a set of characteristics? dream and grants you the answer to one public-health question. You: Pardon? The conversation might go as follows: Creator: As I just said, the true value of a causal incidence You: What is the true effect of (your exposure here, denoted proportion ratio is not necessarily a biological constant. It can by E) on the occurrence of (your disease here, denoted by D)? be different for subgroups of a population. Creator: What do you mean by ‘the true effect’? The true value You: Of course. Everyone in population P. of what parameter? Creator: OK. Comparing what two exposure levels? You: The true relative risk. You: Exposed and unexposed. Creator: Epidemiologists use the term relative risk for several Creator: What do you mean by exposed and unexposed? Exposed different parameters. Which do you mean? for how long, to how much, and during what time period? You: The ratio of average risk with and without exposure—what There are many different ways you could define exposed and some call the risk ratio1 and others call the incidence proportion unexposed, and each of the corresponding possible ratios can ratio.2 have a different true value, you know. Creator: Which incidence proportion ratio? You: Of course. Ever exposed to any amount of E versus never exposed to E. You: Pardon? Creator: The incidence proportion ratio for the causal effect Creator: Do you want a ratio of average disease risk in two on D of ever E compared to never E in population P during the different groups of people with different exposure levels? study time period t0 to t1 is (your causal incidence-proportion- You: Yes. ratio parameter value here). The point of the above is that, while one goal of etiologic a University of Minnesota School of Public Health, Mayo Mail Code 807, 420 epidemiology is to estimate ‘the true effect’ of an exposure on Delaware St. SE, Minneapolis, MN 55455–0392, USA. E-mail: GMPhD@ umn.edu disease frequency, we usually do not precisely specify what b Department of Epidemiology, UCLA School of Public Health, Los Angeles, ‘true effect’ we want to estimate. We may not be able to do so. CA 90095–1772, USA. For example, before reading this paper would you have required 422 422_990019 8/4/2002 4:01 pm Page 423 (Black plate) ESTIMATING CAUSAL EFFECTS 423 less prompting than in the dialog above? How many published of causality theory is provided by Pearl,15 who shows how papers explicitly state what the authors mean by ‘true’ rela- structural-equation models and graphical causal models (causal tive risk or odds ratio, or whether the estimated measure of diagrams) translate directly to counterfactual models, shedding association is intended to have a descriptive or causal inter- light on all three approaches. A brief review of these con- pretation? How many papers explicitly define the population or nections is given by Greenland,21 and Greenland et al.22 provide time period of interest? How many etiologic papers over- a more extensive review of graphical causal modelling for emphasize results that cannot be given a causal interpretation, epidemiological research. such as significance tests, P-values, correlation coefficients, or proportion of variance ‘explained’? Target In this paper we discuss the questions ‘What is a cause?’, We will use the term target population for the group of people ‘How should we measure effects?’ and ‘What effect measure about which our scientific or public-health question asks, and there- should epidemiologists estimate in etiologic studies?’ We begin fore for which we want to estimate the causal effect of an exposure. by adapting the counterfactual approach to causation, originally The target population could be composed of one group of developed in philosophy and in statistics,3,4 to epidemiological people (as in most epidemiological studies), several groups of studies. In the process, we give precise answers to these ques- people (as in an intervention study in several communities), or tions, and we describe how these answers have important one person. For simplicity, in the rest of this discussion we implications for etiologic research: (1) Under the counterfactual assume that the target population is one group of people. approach, the measure we term a ‘causal contrast’ is the only Let the etiologic time period be the time period about which meaningful effect measure for etiologic studies. (2) The counter- our scientific or public-health question asks. The beginning and factual approach provides a general framework for designing end of this time period is specified by the study question. For and analysing epidemiological studies. (3) The counterfactual example, in a study of the effectiveness of a back-injury pre- definition of causal effect shows why direct measurement of an vention programme in a workplace, the etiologic time period effect size is impossible: We must always depend on a sub- could be any time period after the implementation of the stitution step when estimating effects, and the validity of our programme. Note that this period may vary among individuals estimate will thus always depend on the validity of the sub- (e.g. the etiologic time period for a study of weight gain during stitution.3,5–7 (4) The counterfactual approach makes clear that pregnancy and pre-eclampsia spans only pregnancy), and not a critical step in study interpretation is the formal quantification all of the period need be time at risk. For example, the etiologic of bias in study results. (5) The counterfactual approach leads to time period for a study of intrauterine diethylstilbesterol ex- precise definitions of effect measure, confounding, confounder, posure and subsequent fertility problems could include child- and to precise criteria for effect-measure modification. hood, a time at no risk of such problems but during which In the discussion that follows, we assume that the study etiologically relevant events (e.g. puberty) occur. outcome is a disease (e.g. lung cancer); this discussion can be readily extended to any outcome (e.g. a health behaviour such as cigarette smoking). We also assume for simplicity that disease occurrence is deterministic; under a stochastic model, the quantities we discuss are probabilities or expected values.6,7 The counterfactual approach History Let A be the number of new cases of the study disease in the In 1748, the renowned Scottish philosopher David Hume wrote target population during the etiologic time period. Let B be ‘we may define a cause to be an object followed by another … the denominator for computing disease frequency in the target where, if the first object had not been, the second never had population during the etiologic time period. If B is the number existed.’3,8 A key innovation of this definition was that it of people at risk at the beginning of the period and all indi- pivoted on a clause of the form ‘if C had not occurred, D would viduals are followed throughout the etiologic time period, the not have either’, where C and D are what actually occurred. disease-frequency parameter Such a clause, which hypothesizes what would have happened R = A under conditions contrary to actual conditions, is called a B counterfactual conditional. Despite its early appearance, this counterfactual concept of causation received no formal basis is the proportion getting disease over the period (incidence until 1923 when the statistician Jerzy Neyman presented a proportion, average risk). If B is the amount of person-time at quantitative conceptual model for causal analysis.9 This model risk during the period, R is the person-time incidence rate.
Load more

Recommended publications
  • Descriptive Statistics (Part 2): Interpreting Study Results
    Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk.
    [Show full text]
  • Meta-Analysis of Proportions
    NCSS Statistical Software NCSS.com Chapter 456 Meta-Analysis of Proportions Introduction This module performs a meta-analysis of a set of two-group, binary-event studies. These studies have a treatment group (arm) and a control group. The results of each study may be summarized as counts in a 2-by-2 table. The program provides a complete set of numeric reports and plots to allow the investigation and presentation of the studies. The plots include the forest plot, radial plot, and L’Abbe plot. Both fixed-, and random-, effects models are available for analysis. Meta-Analysis refers to methods for the systematic review of a set of individual studies with the aim to combine their results. Meta-analysis has become popular for a number of reasons: 1. The adoption of evidence-based medicine which requires that all reliable information is considered. 2. The desire to avoid narrative reviews which are often misleading. 3. The desire to interpret the large number of studies that may have been conducted about a specific treatment. 4. The desire to increase the statistical power of the results be combining many small-size studies. The goals of meta-analysis may be summarized as follows. A meta-analysis seeks to systematically review all pertinent evidence, provide quantitative summaries, integrate results across studies, and provide an overall interpretation of these studies. We have found many books and articles on meta-analysis. In this chapter, we briefly summarize the information in Sutton et al (2000) and Thompson (1998). Refer to those sources for more details about how to conduct a meta- analysis.
    [Show full text]
  • Philosophy of Science and Philosophy of Chemistry
    Philosophy of Science and Philosophy of Chemistry Jaap van Brakel Abstract: In this paper I assess the relation between philosophy of chemistry and (general) philosophy of science, focusing on those themes in the philoso- phy of chemistry that may bring about major revisions or extensions of cur- rent philosophy of science. Three themes can claim to make a unique contri- bution to philosophy of science: first, the variety of materials in the (natural and artificial) world; second, extending the world by making new stuff; and, third, specific features of the relations between chemistry and physics. Keywords : philosophy of science, philosophy of chemistry, interdiscourse relations, making stuff, variety of substances . 1. Introduction Chemistry is unique and distinguishes itself from all other sciences, with respect to three broad issues: • A (variety of) stuff perspective, requiring conceptual analysis of the notion of stuff or material (Sections 4 and 5). • A making stuff perspective: the transformation of stuff by chemical reaction or phase transition (Section 6). • The pivotal role of the relations between chemistry and physics in connection with the question how everything fits together (Section 7). All themes in the philosophy of chemistry can be classified in one of these three clusters or make contributions to general philosophy of science that, as yet , are not particularly different from similar contributions from other sci- ences (Section 3). I do not exclude the possibility of there being more than three clusters of philosophical issues unique to philosophy of chemistry, but I am not aware of any as yet. Moreover, highlighting the issues discussed in Sections 5-7 does not mean that issues reviewed in Section 3 are less im- portant in revising the philosophy of science.
    [Show full text]
  • Causal Inference with Information Fields
    Causal Inference with Information Fields Benjamin Heymann Michel De Lara Criteo AI Lab, Paris, France CERMICS, École des Ponts, Marne-la-Vallée, France [email protected] [email protected] Jean-Philippe Chancelier CERMICS, École des Ponts, Marne-la-Vallée, France [email protected] Abstract Inferring the potential consequences of an unobserved event is a fundamental scientific question. To this end, Pearl’s celebrated do-calculus provides a set of inference rules to derive an interventional probability from an observational one. In this framework, the primitive causal relations are encoded as functional dependencies in a Structural Causal Model (SCM), which maps into a Directed Acyclic Graph (DAG) in the absence of cycles. In this paper, by contrast, we capture causality without reference to graphs or functional dependencies, but with information fields. The three rules of do-calculus reduce to a unique sufficient condition for conditional independence: the topological separation, which presents some theoretical and practical advantages over the d-separation. With this unique rule, we can deal with systems that cannot be represented with DAGs, for instance systems with cycles and/or ‘spurious’ edges. We provide an example that cannot be handled – to the extent of our knowledge – with the tools of the current literature. 1 Introduction As the world shifts toward more and more data-driven decision-making, causal inference is taking more space in applied sciences, statistics and machine learning. This is because it allows for better, more robust decision-making, and provides a way to interpret the data that goes beyond correlation Pearl and Mackenzie [2018].
    [Show full text]
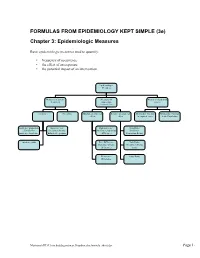
  • FORMULAS from EPIDEMIOLOGY KEPT SIMPLE (3E) Chapter 3: Epidemiologic Measures
    FORMULAS FROM EPIDEMIOLOGY KEPT SIMPLE (3e) Chapter 3: Epidemiologic Measures Basic epidemiologic measures used to quantify: • frequency of occurrence • the effect of an exposure • the potential impact of an intervention. Epidemiologic Measures Measures of disease Measures of Measures of potential frequency association impact (“Measures of Effect”) Incidence Prevalence Absolute measures of Relative measures of Attributable Fraction Attributable Fraction effect effect in exposed cases in the Population Incidence proportion Incidence rate Risk difference Risk Ratio (Cumulative (incidence density, (Incidence proportion (Incidence Incidence, Incidence hazard rate, person- difference) Proportion Ratio) Risk) time rate) Incidence odds Rate Difference Rate Ratio (Incidence density (Incidence density difference) ratio) Prevalence Odds Ratio Difference Macintosh HD:Users:buddygerstman:Dropbox:eks:formula_sheet.doc Page 1 of 7 3.1 Measures of Disease Frequency No. of onsets Incidence Proportion = No. at risk at beginning of follow-up • Also called risk, average risk, and cumulative incidence. • Can be measured in cohorts (closed populations) only. • Requires follow-up of individuals. No. of onsets Incidence Rate = ∑person-time • Also called incidence density and average hazard. • When disease is rare (incidence proportion < 5%), incidence rate ≈ incidence proportion. • In cohorts (closed populations), it is best to sum individual person-time longitudinally. It can also be estimated as Σperson-time ≈ (average population size) × (duration of follow-up). Actuarial adjustments may be needed when the disease outcome is not rare. • In an open populations, Σperson-time ≈ (average population size) × (duration of follow-up). Examples of incidence rates in open populations include: births Crude birth rate (per m) = × m mid-year population size deaths Crude mortality rate (per m) = × m mid-year population size deaths < 1 year of age Infant mortality rate (per m) = × m live births No.
    [Show full text]
  • The Practice of Causal Inference in Cancer Epidemiology
    Vol. 5. 303-31 1, April 1996 Cancer Epidemiology, Biomarkers & Prevention 303 Review The Practice of Causal Inference in Cancer Epidemiology Douglas L. Weedt and Lester S. Gorelic causes lung cancer (3) and to guide causal inference for occu- Preventive Oncology Branch ID. L. W.l and Comprehensive Minority pational and environmental diseases (4). From 1965 to 1995, Biomedical Program IL. S. 0.1. National Cancer Institute, Bethesda, Maryland many associations have been examined in terms of the central 20892 questions of causal inference. Causal inference is often practiced in review articles and editorials. There, epidemiologists (and others) summarize evi- Abstract dence and consider the issues of causality and public health Causal inference is an important link between the recommendations for specific exposure-cancer associations. practice of cancer epidemiology and effective cancer The purpose of this paper is to take a first step toward system- prevention. Although many papers and epidemiology atically reviewing the practice of causal inference in cancer textbooks have vigorously debated theoretical issues in epidemiology. Techniques used to assess causation and to make causal inference, almost no attention has been paid to the public health recommendations are summarized for two asso- issue of how causal inference is practiced. In this paper, ciations: alcohol and breast cancer, and vasectomy and prostate we review two series of review papers published between cancer. The alcohol and breast cancer association is timely, 1985 and 1994 to find answers to the following questions: controversial, and in the public eye (5). It involves a common which studies and prior review papers were cited, which exposure and a common cancer and has a large body of em- causal criteria were used, and what causal conclusions pirical evidence; over 50 studies and over a dozen reviews have and public health recommendations ensued.
    [Show full text]
  • Statistics and Causal Inference (With Discussion)
    Applied Statistics Lecture Notes Kosuke Imai Department of Politics Princeton University February 2, 2008 Making statistical inferences means to learn about what you do not observe, which is called parameters, from what you do observe, which is called data. We learn the basic principles of statistical inference from a perspective of causal inference, which is a popular goal of political science research. Namely, we study statistics by learning how to make causal inferences with statistical methods. 1 Statistical Framework of Causal Inference What do we exactly mean when we say “An event A causes another event B”? Whether explicitly or implicitly, this question is asked and answered all the time in political science research. The most commonly used statistical framework of causality is based on the notion of counterfactuals (see Holland, 1986). That is, we ask the question “What would have happened if an event A were absent (or existent)?” The following example illustrates the fact that some causal questions are more difficult to answer than others. Example 1 (Counterfactual and Causality) Interpret each of the following statements as a causal statement. 1. A politician voted for the education bill because she is a democrat. 2. A politician voted for the education bill because she is liberal. 3. A politician voted for the education bill because she is a woman. In this framework, therefore, the fundamental problem of causal inference is that the coun- terfactual outcomes cannot be observed, and yet any causal inference requires both factual and counterfactual outcomes. This idea is formalized below using the potential outcomes notation.
    [Show full text]
  • Bayesian Causal Inference
    Bayesian Causal Inference Maximilian Kurthen Master’s Thesis Max Planck Institute for Astrophysics Within the Elite Master Program Theoretical and Mathematical Physics Ludwig Maximilian University of Munich Technical University of Munich Supervisor: PD Dr. Torsten Enßlin Munich, September 12, 2018 Abstract In this thesis we address the problem of two-variable causal inference. This task refers to inferring an existing causal relation between two random variables (i.e. X → Y or Y → X ) from purely observational data. We begin by outlining a few basic definitions in the context of causal discovery, following the widely used do-Calculus [Pea00]. We continue by briefly reviewing a number of state-of-the-art methods, including very recent ones such as CGNN [Gou+17] and KCDC [MST18]. The main contribution is the introduction of a novel inference model where we assume a Bayesian hierarchical model, pursuing the strategy of Bayesian model selection. In our model the distribution of the cause variable is given by a Poisson lognormal distribution, which allows to explicitly regard discretization effects. We assume Fourier diagonal covariance operators, where the values on the diagonal are given by power spectra. In the most shallow model these power spectra and the noise variance are fixed hyperparameters. In a deeper inference model we replace the noise variance as a given prior by expanding the inference over the noise variance itself, assuming only a smooth spatial structure of the noise variance. Finally, we make a similar expansion for the power spectra, replacing fixed power spectra as hyperparameters by an inference over those, where again smoothness enforcing priors are assumed.
    [Show full text]
  • Experience Verification Form
    Tennessee Department of Education – Office of Educator Licensure Experience Verification Form The information listed below is to be completed by the current or previous employer (Superintendent, Headmaster, Agency Director, or Designated Personnel Officer). Principals are not authorized to sign this form unless they are the designated personnel officer. Use one line for each change in status. Do not include leave of absence periods. Only include experience that is not in the TN state data system. Name of Educator: ________________________________________________ Social Security Number: _________________________ Information below to be completed by the SCHOOL SYSTEM where the teaching was performed. Experience Record: Please list experience yearly, each year on a separate line, beginning with July 1 and ending June 30. Name School Position Fiscal Year, July 01 - June 30 Time Employed % Time, Total of System and State Beginning Date Ending Date Months / Days Ex. Part-time, Days in Month/Day/Year Month/Day/Year Full-time School Year School Grade Level Per Year Check one of the following: Public School Private School * Charter School * U.S. Government Service Teaching Program * ** Please note: If non-public school you must identify accreditation. The above school/school system was fully approved or accredited by the ____________________________________________________________________ at the time the service was performed. (State Department of Education, or Regional Association of Colleges & Schools, or recognized private school accrediting
    [Show full text]
  • C.S. Peirce's Abduction from the Prior Analytics
    Providence College DigitalCommons@Providence Community Scholar Publications Providence College Community Scholars 7-1996 C.S. Peirce's Abduction from the Prior Analytics William Paul Haas Follow this and additional works at: https://digitalcommons.providence.edu/comm_scholar_pubs Haas, William Paul, "C.S. Peirce's Abduction from the Prior Analytics" (1996). Community Scholar Publications. 2. https://digitalcommons.providence.edu/comm_scholar_pubs/2 This Article is brought to you for free and open access by the Providence College Community Scholars at DigitalCommons@Providence. It has been accepted for inclusion in Community Scholar Publications by an authorized administrator of DigitalCommons@Providence. For more information, please contact [email protected]. WILLIAM PAUL HAAS July 1996 C.S. PEIRCE'S ABDUCTION FROM THE PRIOR ANALYTICS In his Ancient Formal Logic. Professor Joseph Bochenski finds Aristotle's description of syllogisms based upon hypotheses to be "difficult to understand." Noting that we do not have the treatise which Aristotle promised to write, Bochenski laments the fact that the Prior Analytics, where it is treated most explicitly, "is either corrupted or (which is more probable) was hastily written and contains logical errors." (1) Charles Sanders Peirce wrestled with the same difficult text when he attempted to establish the Aristotelian roots of his theory of abductive or hypothetical reasoning. However, Peirce opted for the explanation that the fault was with the corrupted text, not with Aristotle's exposition. Peirce interpreted the text of Book II, Chapter 25 thus: Accordingly, when he opens the next chapter with the word ' Ajray (¿y-q a word evidently chosen to form a pendant to 'Errctyuyrj, we feel sure that this is what he is coming to.
    [Show full text]
  • Changes to the Standard to Implement the Safer Choice Label (Pdf)
    Changes to the Standard to Implement the Safer Choice Label 2/10/15 Implementation of a New Label for the DfE Safer Product Labeling Program and Supporting Modifications to the DfE Standard for Safer Products, now to be known as the “Safer Choice Standard,” including the Designation of a Fragrance-Free Label This document explains several important changes to EPA’s Safer Product Labeling Program (SPLP), as well as a number of conforming changes to the program’s Standard for Safer Products, including: a new label1 and name for the EPA SPLP; an associated fragrance-free label; and related changes to the standard that qualifies products for the label. With this document EPA is finalizing the new label for immediate use. While effective immediately, the Agency is requesting comment on the other changes described in this document, including a new, optional fragrance-free certification. Redesigned Label The EPA Design for the Environment (DfE) Safer Product Labeling Program has redesigned its label to better communicate the program’s human health and environmental protection goals, increase consumer and institutional/industrial purchaser understanding and recognition of products bearing the label, and encourage innovation and the development of safer chemicals and chemical-based products. The label’s new name “Safer Choice,” with the accompanying wording (or “tagline”) “Meets U.S. EPA Safer Product Standards” (which is part of the label), and design were developed over many months based on input and feedback from a diverse set of stakeholders and the general public. This input and feedback included more than 1700 comments on EPA’s website, six consumer focus group sessions in three geographic markets, and a national online survey.
    [Show full text]
  • Articles Causal Inference in Civil Rights Litigation
    VOLUME 122 DECEMBER 2008 NUMBER 2 © 2008 by The Harvard Law Review Association ARTICLES CAUSAL INFERENCE IN CIVIL RIGHTS LITIGATION D. James Greiner TABLE OF CONTENTS I. REGRESSION’S DIFFICULTIES AND THE ABSENCE OF A CAUSAL INFERENCE FRAMEWORK ...................................................540 A. What Is Regression? .........................................................................................................540 B. Problems with Regression: Bias, Ill-Posed Questions, and Specification Issues .....543 1. Bias of the Analyst......................................................................................................544 2. Ill-Posed Questions......................................................................................................544 3. Nature of the Model ...................................................................................................545 4. One Regression, or Two?............................................................................................555 C. The Fundamental Problem: Absence of a Causal Framework ....................................556 II. POTENTIAL OUTCOMES: DEFINING CAUSAL EFFECTS AND BEYOND .................557 A. Primitive Concepts: Treatment, Units, and the Fundamental Problem.....................558 B. Additional Units and the Non-Interference Assumption.............................................560 C. Donating Values: Filling in the Missing Counterfactuals ...........................................562 D. Randomization: Balance in Background Variables ......................................................563
    [Show full text]