DOCSLIB.ORG

MT-200: Minimizing Jitter in ADC Clock Interfaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
MT-200: Minimizing Jitter in ADC Clock Interfaces Applications Engineering Notebook MT-200 One Technology Way • P. O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: 781.329.4700 • Fax: 781.461.3113 • www.analog.com Minimizing Jitter in ADC Clock Interfaces by the Applications Engineering Group POWER SUPPLY Analog Devices, Inc. INPUT V REF DATA ANALOG OUTPUT IN THIS NOTEBOOK INPUT ADC Since jitter around the threshold region of a clock interface CLOCK FPGA INTERFACE can corrupt the dynamic performance of an analog-to- INPUT CONTROL digital converter (ADC), this notebook provides an overview of clocking considerations and jitter-reduction techniques. The Applications Engineering Notebook Educational Series TABLE OF CONTENTS Clock Input Noise.............................................................................. 2 Frequency Domain View ............................................................. 3 Time Domain View ....................................................................... 2 Phase Domain View ..................................................................... 4 Effect of Slew Rate..................................................................... 3 Solutions for Clocking Converters ............................................. 5 REVISION HISTORY 1/12—Revision 0: Initial Version Rev. 0 | Page 1 of 8 MT-200 Applications Engineering Notebook CLOCK INPUT NOISE Jitter around the threshold region of the clock interface can TIME DOMAIN VIEW corrupt the timing of an analog-to-digital converter (ADC). For example, jitter can cause the ADC to capture a sample at the wrong time, resulting in false sampling of the analog input and reducing the signal to noise (SNR) ratio of the device. A reduction in jitter can be achieved in a number of different ways, including improving the clock source, filtering, frequency division, and clock circuit hardware. This document provides dV suggestions on how to improve the clock system to achieve the best possible performance from an ADC. Noise in the circuit between the clock and ADC is the root ERROR VOLTAGE cause of clock jitter. Random jitter is caused by random noise, which is distinguished by its unbounded character and follows statistical distributions. Major random noise sources include • Thermal (Johnson or Nyquist) noise is caused by Brownian ENCODE motion of the charge carriers. • Shot noise is related to the dc current flow across a Q1 potential barrier that is not continuous and smooth, but RECTANGULAR instead is the result of pulses of current caused by the BI-MODEL individual flow of carriers. NORMAL • Flicker noise occurs when a dc current is flowing. It is IDEAL 10338-001 caused by traps in semiconductors that hold carriers that Figure 1. Time Domain View of Jitter would normally constitute a dc current flow for a short period before releasing them. Clock jitter is the sample-to-sample variation of the encode • Burst, or popcorn, noise is caused by contamination and clock which includes both external and internal jitter. Full-scale crystal lattice dislocation at the surface of the silicon that SNR is jitter limited by captures and releases carriers in a random manner. S 1 SNR = rms = log(20)log(20 ) jitter N 2π tf Deterministic jitter is caused by interference that shifts the rms ana log jitter threshold in certain ways that are usually bounded by nature. For example, at 1 Ghz with 100 FS rms jitter, the SNR is 64 dB. There are three ways to view the noise in a clock signal: Viewed in the time domain, variation of the encode edge in • Time domain the x-axis direction causes a y-axis error with a magnitude • Frequency domain dependent on the rise time of the edge. Aperture jitter produces • Phase domain errors in the ADC output as shown in Figure 2. The jitter can occur internally in the ADC or externally in the sampling clock or interface circuitry. dV ΔV = × Δt dt ANALOG INPUT dV = SLOPE ΔVRMS = APERTURE JITTER ERROR dt NOMINAL HELD OUTPUT ΔtRMS = APERTURE JITTER HOLD TRACK 10338-002 Figure 2. Effects of Aperture Jitter and Sampling Clock Jitter Rev. 0 | Page 2 of 8 Applications Engineering Notebook MT-200 Figure 3 shows the effects of jitter on SNR. Five traces are the slew rate. Figure 5 shows how increasing the slew rate shown in Figure 3, each representing a different value of jitter. reduces jitter because only noises in the threshold range The x-axis is full-scale analog input frequency, and the y-axis is contribute to jitter. the SNR due to the jitter as opposed to the total ADC SNR. 200 Jitter on a clock is defined from the fSTART and fSTOP offset frequency. For example, a clock may have 200 fsec of jitter integrated from 1 kHz to fs/2 and 170 fsec of jitter integrated 150 from 10 kHz to fs/2. The integration range is dependent upon the end application. 90 100 SNR OF ADC AT 200MHz, AIN VARIES WITH CLOCK JITTER DIGITAL 85 ADC OUTPUT 84dB JITTER RMS (fs) ANALOG 80 INPUT 78dB SAMPLING 50 CLOCK 75 TIO (dB) A 50 72dB fS 70 100f 0 66dB S 0 2 4 6 65 O NOISE R O NOISE INPUT SLEW RATE (V/ns) 10338-005 200fS LT 60 60dB Figure 5. Increasing Slew Rate Reduces Jitter AIN = 200MHz 400fS SIGNA 55 FREQUENCY DOMAIN VIEW 1 EACH LINE SHOWS 50 800fS SNRjit = 20log CONSTANT RMS Close-in noise occurs in the region between the center 2πftjitter CLOCK JITTER IN fs 45 frequency of the sample clock to a single sideband (SSB) offset 100 1000 equal to half the signal bandwidth. Wideband noise extends FULL-SCALE ANALOG INPUT (MHz) 10338-003 Figure 3. As Analog Signal Increases, Clock Jitter Increases SNR from the SSB offset to ½ the bandwidth of the clock receiver. The jitter-based SNR and the effective number of bits (ENOB) are related by the equation: SNR = 6.02 N + 1.76 dB where N = ENOB. For full-scale 100 MHz input, 14-bit ENOB requires that the rms jitter be no greater than 0.125 ps or 125 fs. The equation assumes an ADC of infinite resolution where the only error is noise produced by the clock jitter. CLOSE IN NOISE 130 RMS JITTER < 1ps 0.125ps 120 IS VERY HIGH 0.25ps PERFORMANCE TO ENCODE 0.5ps TO DC WITH CLOCK BANDWIDTH 110 1ps 1 NOISE PHASE 2ps SNR = 20 log 10 2 ft 100 jitter 16 BITS TE (dB) A 90 WIDEBAND 14 BITS NOISE 10338-006 80 Figure 6. Frequency Domain View 12 BITS ENOB O NOISE R O NOISE 70 LT Multiplication in time is convolution in the frequency domain. 10 BITS 60 Therefore, any skirt on the clock is applied to the digitized SIGNA 50 signal. This increases the EVM of the signal and degrades IF SAMPLING ADCs 40 ANALOG FREQUENCY 70MHz TO 300MHz, overall performance. The amount convolved onto the sample SNR 60dB TO 80dB signal depends on the relationship of the analog frequency to 30 1 10 100 1000 the sample frequency. FULL-SCALE ANALOG INPUTFREQUENCY (MHz) 10338-004 fsignal Figure 4. Theoretical SNR and ENOB Due Jitter as a Function of Full-Scale SampledOutput = lClockSigna + )log(20 Sinewave Analog Input Frequency fclock Effect of Slew Rate Increasing the slew rate of the clock edge reduces the effects of noise and jitter by leaving the circuit less exposed. On the other hand, a faster slew rate increases the difficulty of circuit design, may cause electromagnetic interference (EMI) issues and may cause interference in other circuits. Note that an oscilloscope with very low input capacitance is needed to accurately measure Rev. 0 | Page 3 of 8 MT-200 Applications Engineering Notebook –120 The spur is at −74.1 dBc as determined by the following –120 –125 equation: 62.30 –130 +− log(2066 −= 1.74) dBc 78 –135 –10 –140 –20 –145 –30 PHASE NOISE (dBc/Hz) PHASE –150 –40 –50 –155 dBc –60 –160 10 100 1k 10k 100k 1M 10M 100M –70 FREQUENCY (Hz) –80 –90 –100 30.25 30.50 30.75 31.00 31.25 FREQUENCY (MHz) 10338-009 Figure 9. 30.62 MHz Signal when Sampled with a Noisy Clock Clock designers typically provide a phase noise, but not a jitter L specification. The phase noise specification can be converted to jitter by first determining the noise on the clock and then comparing noise to the main clock component using small angle math. DESIRED SIGNA The phase noise power is integrated by calculating the gray area PHASE PHASE NOISE NOISE in Figure 10. SKIRTS SKIRTS 10338-007 Figure 7. The Noise Convolved onto the Sampled Signal Depends on the rise Vphase_noise Relationship of the Analog Frequency to the Sample Frequency Ф ≈ run = Vmain_clock PHASE DOMAIN VIEW MODULATION ANGLE Ф Phase noise is cause by variations in the time period between MAIN each clock cycle. The end result is that the clock signal varies COMPONENT PHASE NOISE OF CLOCK COMPONENT around a fundamental frequency. This spread of frequencies OF CLOCK will degrade the ADC’s SNR. ANGULAR RATE OF ENCODE CLOCK SAMPLE INSTANT: PHASE = 0 i.e. POSITIVE GOING ANGULAR RATE OF 0 CROSSING ENCODE CLOCK INTEGRATE TO ENCODE BANDWIDTH –160 PHASE NOISE (dBc/Hz) PHASE PHASE, 10k 100k 1M 10M 100M 1G FREQUENCY AND (Hz) 10338-010 AMPLITUDE NOISE ON CLOCK Figure 10. Integrating the Noise from Close-In to the Clock Out to the 10338-008 Bandwidth of the Encode Figure 8. Phase Domain View of Jitter The height is −160 dBc and the width is 10 KHz to 245.76 MHz. In the example shown below, a spur is added to a 78 MHz Therefore, 10×log(245.7e6 − 10e3) = 83.9 dB and −160 + 83.9 dB clock at level of −66 dBc and is used to control an ADC = 76.1 dBc of integrated noise. sampling a 30.62 MHz analog signal. Rev. 0 | Page 4 of 8 Applications Engineering Notebook MT-200 6 3 PNoise = −160dBc /Hz + 10log(245.76× 10 − 10.0 × 10 = − 76.1 dBc PNoise /10= −76.1/10 −4 Jitterphase ≅2 × 10 =2 × 10 =2.217 × 10 radians for small angles Jitter 2.217× 10−4 Jitter = Phase = = .1435pS 6 2πfOsc 2π × 245.76 × 10 At different offsets from the carrier, the slope of the noise can 2 + 10 × log(30 )M=- 87.3 dBc be different.
Load more

Recommended publications
  • Johnson Noise and Shot Noise: the Determination of the Boltzmann Constant, Absolute Zero Temperature and the Charge of the Electron
    Johnson Noise and Shot Noise: The Determination of the Boltzmann Constant, Absolute Zero Temperature and the Charge of the Electron MIT Department of Physics (Dated: September 3, 2013) In electronic measurements, one observes \signals," which must be distinctly above the \noise." Noise induced from outside sources may be reduced by shielding and proper \grounding." Less noise means greater sensitivity with signal/noise as the figure of merit. However, there exist fundamental sources of noise which no clever circuit can avoid. The intrinsic noise is a result of the thermal jitter of the charge carriers and the quantization of charge. The purpose of this experiment is to measure these two limiting electrical noises. From the measurements, values of the Boltzmann constant and the charge of the electron will be derived. PREPARATORY QUESTIONS By the end of the 19th century, the accumulated ev- idence from chemistry, crystallography, and the kinetic Please visit the Johnson and Shot Noise chapter on the theory of gases left little doubt about the validity of the 8.13x website at mitx.mit.edu to review the background atomic theory of matter. Nevertheless, there were still material for this experiment. Answer all questions found arguments against the atomic theory, stemming from a in the chapter. Work out the solutions in your laboratory lack of "direct" evidence for the reality of atoms. In fact, notebook; submit your answers on the web site. there was no precise measurement yet available of the quantitative relation between atoms and the objects of direct scientific experience such as weights, meter sticks, EXPERIMENT GOALS clocks, and ammeters.
    [Show full text]
  • Understanding Jitter and Wander Measurements and Standards Second Edition Contents
    Understanding Jitter and Wander Measurements and Standards Second Edition Contents Page Preface 1. Introduction to Jitter and Wander 1-1 2. Jitter Standards and Applications 2-1 3. Jitter Testing in the Optical Transport Network 3-1 (OTN) 4. Jitter Tolerance Measurements 4-1 5. Jitter Transfer Measurement 5-1 6. Accurate Measurement of Jitter Generation 6-1 7. How Tester Intrinsics and Transients 7-1 affect your Jitter Measurement 8. What 0.172 Doesn’t Tell You 8-1 9. Measuring 100 mUIp-p Jitter Generation with an 0.172 Tester? 9-1 10. Faster Jitter Testing with Simultaneous Filters 10-1 11. Verifying Jitter Generator Performance 11-1 12. An Overview of Wander Measurements 12-1 Acronyms Welcome to the second edition of Agilent Technologies Understanding Jitter and Wander Measurements and Standards booklet, the distillation of over 20 years’ experience and know-how in the field of telecommunications jitter testing. The Telecommunications Networks Test Division of Agilent Technologies (formerly Hewlett-Packard) in Scotland introduced the first jitter measurement instrument in 1982 for PDH rates up to E3 and DS3, followed by one of the first 140 Mb/s jitter testers in 1984. SONET/SDH jitter test capability followed in the 1990s, and recently Agilent introduced one of the first 10 Gb/s Optical Channel jitter test sets for measurements on the new ITU-T G.709 frame structure. Over the years, Agilent has been a significant participant in the development of jitter industry standards, with many contributions to ITU-T O.172/O.173, the standards for jitter test equipment, and Telcordia GR-253/ ITU-T G.783, the standards for operational SONET/SDH network equipment.
    [Show full text]
  • Retrospective Analysis of Phonatory Outcomes After CO2 Laser Thyroarytenoid 00111 Myoneurectomy in Patients with Adductor Spasmodic Dysphonia
    Global Journal of Otolaryngology ISSN 2474-7556 Research Article Glob J Otolaryngol Volume 22 Issue 4- June 2020 Copyright © All rights are reserved by Rohan Bidaye DOI: 10.19080/GJO.2020.22.556091 Retrospective Analysis of Phonatory Outcomes after CO2 Laser Thyroarytenoid Myoneurectomy in Patients with Adductor Spasmodic Dysphonia Rohan Bidaye1*, Sachin Gandhi2*, Aishwarya M3 and Vrushali Desai4 1Senior Clinical Fellow in Laryngology, Deenanath Mangeshkar Hospital, India 2Head of Department of ENT, Deenanath Mangeshkar Hospital, India 3Fellow in Laryngology, Deenanath Mangeshkar Hospital, India 4Chief Consultant, Speech Language Pathologist, Deenanath Mangeshkar Hospital, India Submission: May 16, 2020; Published: June 08, 2020 *Corresponding author: Rohan Bidaye and Sachin Gandhi, Senior Clinical Fellow in Laryngology and Head of Department of ENT, Deenanath Mangeshkar Hospital, India Abstract Introduction: Adductor spasmodic dysphonia (ADSD) is a focal laryngeal dystonia characterized by spasms of laryngeal muscles during speech. Botulinum toxin injection in the Thyroarytenoid muscle remains the gold-standard treatment for ADSD. However, as Botulinum toxin CO2 laser Thyroarytenoid myoneurectomy (TAM) has been reported as an effective technique for treatment of ADSD. It provides sustained improvementinjections need in tothe be voice repeated over a periodically,longer duration. the voice quality fluctuates over a longer period. A Microlaryngoscopic Transoral approach to Methods: Trans oral Microlaryngoscopic CO2 laser TAM was performed in 14 patients (5 females and 9 males), aged between 19 and 64 years who were diagnosed with ADSD. Data was collected from over 3 years starting from Jan 2014 – Dec 2016. GRBAS scale along with Multi- dimensional voice programme (MDVP) analysis of the voice and Video laryngo-stroboscopic (VLS) samples at the end of 3 and 12 months of surgery would be compared with the pre-operative readings.
    [Show full text]
  • Perturbation and Harmonics to Noise Ratio As a Function of Gender in the Aged Voice
    Perturbation and Harmonics to Noise Ratio as a Function of Gender in the Aged Voice THESIS Presented in Partial Fulfillment of the Requirements for the Degree Master of Arts in the Graduate School of The Ohio State University By Meredith Margaret Rouse Hunt Graduate Program in Speech and Hearing Science The Ohio State University 2012 Master's Examination Committee: Michael Trudeau, Advisor Michelle Bourgeois Copyrighted by Meredith Margaret Rouse Hunt 2012 Abstract The purpose of this investigation was to explore possible differences as a function of gender in perturbation (jitter and shimmer) and harmonics to noise ratio (HNR) among aged male and female speakers. Thirty normal aged adults (15 males; 15 females; over age 60) prolonged the vowel /a/ at a comfortable loudness level. Measures of jitter (%), shimmer (%), and HNR were used to compare vocal function between aged gender groups. No significant differences were found between genders on any of the measures. Findings are discussed relative to other published studies on similar measures and support data that aged voices exhibit increased variability. Future suggestions for research are discussed. ii Dedication This manuscript is dedicated to my husband, Ryan, for his unfailing patience, support, and humor during the completion of my thesis and in all aspects of my life. iii Acknowledgments I would like to acknowledge Michael Trudeau, Ph. D., CCC-SLP, my academic and thesis advisor, for his gentle and persistent guidance. His dedication to teaching and patience with students has allowed me to become adept at critical evaluations of research and treatment methodology. More importantly, his love of voice science and care for his clients has shaped my future professional career as speech-language pathologist.
    [Show full text]
  • 22Nd International Congress on Acoustics ICA 2016
    Page intentionaly left blank 22nd International Congress on Acoustics ICA 2016 PROCEEDINGS Editors: Federico Miyara Ernesto Accolti Vivian Pasch Nilda Vechiatti X Congreso Iberoamericano de Acústica XIV Congreso Argentino de Acústica XXVI Encontro da Sociedade Brasileira de Acústica 22nd International Congress on Acoustics ICA 2016 : Proceedings / Federico Miyara ... [et al.] ; compilado por Federico Miyara ; Ernesto Accolti. - 1a ed . - Gonnet : Asociación de Acústicos Argentinos, 2016. Libro digital, PDF Archivo Digital: descarga y online ISBN 978-987-24713-6-1 1. Acústica. 2. Acústica Arquitectónica. 3. Electroacústica. I. Miyara, Federico II. Miyara, Federico, comp. III. Accolti, Ernesto, comp. CDD 690.22 ISBN 978-987-24713-6-1 © Asociación de Acústicos Argentinos Hecho el depósito que marca la ley 11.723 Disclaimer: The material, information, results, opinions, and/or views in this publication, as well as the claim for authorship and originality, are the sole responsibility of the respective author(s) of each paper, not the International Commission for Acoustics, the Federación Iberoamaricana de Acústica, the Asociación de Acústicos Argentinos or any of their employees, members, authorities, or editors. Except for the cases in which it is expressly stated, the papers have not been subject to peer review. The editors have attempted to accomplish a uniform presentation for all papers and the authors have been given the opportunity to correct detected formatting non-compliances Hecho en Argentina Made in Argentina Asociación de Acústicos Argentinos, AdAA Camino Centenario y 5006, Gonnet, Buenos Aires, Argentina http://www.adaa.org.ar Proceedings of the 22th International Congress on Acoustics ICA 2016 5-9 September 2016 Catholic University of Argentina, Buenos Aires, Argentina ICA 2016 has been organised by the Ibero-american Federation of Acoustics (FIA) and the Argentinian Acousticians Association (AdAA) on behalf of the International Commission for Acoustics.
    [Show full text]
  • Johnson Noise Thermometry Measurement of the Boltzmann Constant with a 200 Ω Sense Resistor Alessio Pollarolo, Taehee Jeong, Samuel P
    1512 IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, VOL. 62, NO. 6, JUNE 2013 Johnson Noise Thermometry Measurement of the Boltzmann Constant With a 200 Ω Sense Resistor Alessio Pollarolo, Taehee Jeong, Samuel P. Benz, Senior Member, IEEE, and Horst Rogalla, Member, IEEE Abstract—In 2010, the National Institute of Standards and Technology measured the Boltzmann constant k with an electronic technique that measured the Johnson noise of a 100 Ω resistor at the triple point of water and used a voltage waveform synthesized with a quantized voltage noise source (QVNS) as a reference. In this paper, we present measurements of k using a 200 Ω sense re- sistor and an appropriately modified QVNS circuit and waveform. Preliminary results show agreement with the previous value within the statistical uncertainty. An analysis is presented, where the largest source of uncertainty is identified, which is the frequency dependence in the constant term a0 of the two-parameter fit. Index Terms—Boltzmann equation, Josephson junction, mea- surement units, noise measurement, standards, temperature. Fig. 1. Schematic diagram of the Johnson-noise two-channel cross-correlator. I. INTRODUCTION HE Johnson–Nyquist equation (1) defines the thermal measurement electronics are calibrated by using a pseudonoise T noise power (Johnson noise) V 2 of a resistor in a voltage waveform synthesized with the quantized voltage noise bandwidth Δf through its resistance R and its thermodynamic source (QVNS) that acts as a spectral-density reference [8], [9]. temperature T [1], [2]: Fig. 1 shows the experimental schematic. The two chan- nels of the cross-correlator simultaneously amplify, filter, and 2 VR =4kTRΔf.
    [Show full text]
  • PROCEEDINGS of the ICA CONGRESS (Onl the ICA PROCEEDINGS OF
    ine) - ISSN 2415-1599 ISSN ine) - PROCEEDINGS OF THE ICA CONGRESS (onl THE ICA PROCEEDINGS OF Page intentionaly left blank 22nd International Congress on Acoustics ICA 2016 PROCEEDINGS Editors: Federico Miyara Ernesto Accolti Vivian Pasch Nilda Vechiatti X Congreso Iberoamericano de Acústica XIV Congreso Argentino de Acústica XXVI Encontro da Sociedade Brasileira de Acústica 22nd International Congress on Acoustics ICA 2016 : Proceedings / Federico Miyara ... [et al.] ; compilado por Federico Miyara ; Ernesto Accolti. - 1a ed . - Gonnet : Asociación de Acústicos Argentinos, 2016. Libro digital, PDF Archivo Digital: descarga y online ISBN 978-987-24713-6-1 1. Acústica. 2. Acústica Arquitectónica. 3. Electroacústica. I. Miyara, Federico II. Miyara, Federico, comp. III. Accolti, Ernesto, comp. CDD 690.22 ISSN 2415-1599 ISBN 978-987-24713-6-1 © Asociación de Acústicos Argentinos Hecho el depósito que marca la ley 11.723 Disclaimer: The material, information, results, opinions, and/or views in this publication, as well as the claim for authorship and originality, are the sole responsibility of the respective author(s) of each paper, not the International Commission for Acoustics, the Federación Iberoamaricana de Acústica, the Asociación de Acústicos Argentinos or any of their employees, members, authorities, or editors. Except for the cases in which it is expressly stated, the papers have not been subject to peer review. The editors have attempted to accomplish a uniform presentation for all papers and the authors have been given the opportunity
    [Show full text]
  • Clock Jitter Effects on the Performance of ADC Devices
    Clock Jitter Effects on the Performance of ADC Devices Roberto J. Vega Luis Geraldo P. Meloni Universidade Estadual de Campinas - UNICAMP Universidade Estadual de Campinas - UNICAMP P.O. Box 05 - 13083-852 P.O. Box 05 - 13083-852 Campinas - SP - Brazil Campinas - SP - Brazil [email protected] [email protected] Karlo G. Lenzi Centro de Pesquisa e Desenvolvimento em Telecomunicac¸oes˜ - CPqD P.O. Box 05 - 13083-852 Campinas - SP - Brazil [email protected] Abstract— This paper aims to demonstrate the effect of jitter power near the full scale of the ADC, the noise power is on the performance of Analog-to-digital converters and how computed by all FFT bins except the DC bin value (it is it degrades the quality of the signal being sampled. If not common to exclude up to 8 bins after the DC zero-bin to carefully controlled, jitter effects on data acquisition may severely impacted the outcome of the sampling process. This analysis avoid any spectral leakage of the DC component). is of great importance for applications that demands a very This measure includes the effect of all types of noise, the good signal to noise ratio, such as high-performance wireless distortion and harmonics introduced by the converter. The rms standards, such as DTV, WiMAX and LTE. error is given by (1), as defined by IEEE standard [5], where Index Terms— ADC Performance, Jitter, Phase Noise, SNR. J is an exact integer multiple of fs=N: I. INTRODUCTION 1 s X = jX(k)j2 (1) With the advance of the technology and the migration of the rms N signal processing from analog to digital, the use of analog-to- k6=0;J;N−J digital converters (ADC) became essential.
    [Show full text]
  • Effective Bits
    Application Note Effective Bits Effective Bits Testing Evaluates Dynamic Performance of Digitizing Instruments The Effective Bits Concept desired time resolution, run the digitizer at the requisite Whether you are designing or buying a digitizing sys- sampling rate. Those are simple enough answers. tem, you need some means of determining actual, Unfortunately, they can be quite misleading, too. real-life digitizing performance. How closely does the While an “8-bit digitizer” might provide close to eight output of any given analog-to-digital converter (ADC), bits of accuracy and resolution on DC or slowly waveform digitizer or digital storage oscilloscope changing signals, that will not be the case for higher actually follow any given analog input signal? speed signals. Depending on the digitizing technology At the most basic level, digitizing performance would used and other system factors, dynamic digitizing seem to be a simple matter of resolution. For the performance can drop markedly as signal speeds desired amplitude resolution, pick a digitizer with the increase. An 8-bit digitizer can drop to 6-bit, 4-bit, requisite number of “bits” (quantizing levels). For the or even fewer effective bits of performance well before reaching its specified bandwidth. Effective Bits Application Note Figure 1. When comparing digitizer performance, testing the full frequency range is important. If you are designing an ADC device, a digitizing instru- components. Thus, it may be necessary to do an ment, or a test system, it is important to understand the effective bits evaluation for purposes of comparison. If various factors affecting digitizing performance and to equipment is to be combined into a system, an effective have some means of overall performance evaluation.
    [Show full text]
  • The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel
    AN-1067 APPLICATION NOTE One Technology Way • P. O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: 781.329.4700 • Fax: 781.461.3113 • www.analog.com The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel INTRODUCTION GENERAL DESCRIPTION Jitter on analog-to-digital and digital-to-analog converter sam- There are numerous techniques for generating clocks used in pling clocks presents a limit to the maximum signal-to-noise electronic equipment. Circuits include R-C feedback circuits, ratio that can be achieved (see Integrated Analog-to-Digital and timers, oscillators, and crystals and crystal oscillators. Depend- Digital-to-Analog Converters by van de Plassche in the References ing on circuit requirements, less expensive sources with higher section). In this application note, phase noise and jitter are defined. phase noise (jitter) may be acceptable. However, recent devices The power spectral density of phase noise and jitter is developed, demand better clock performance and, consequently, more time domain and frequency domain measurement techniques costly clock sources. Similar demands are placed on the spectral are described, limitations of laboratory equipment are explained, purity of signals sampled by converters, especially frequency and correction factors to these techniques are provided. The synthesizers used as sources in the testing of current higher theory presented is supported with experimental results applied performance converters. In the following section, definitions to a real world problem. of phase noise and jitter are presented. Then a mathematical derivation is developed relating phase noise and jitter to their frequency representation.
    [Show full text]
  • LNCS 4523, Pp
    中国科技论文在线 http://www.paper.edu.cn Jitter Distribution Evaluation and Suppression Method in UWB Systems Weihua Zhang, Hanbing Shen, Zhiquan Bai, and Kyung Sup Kwak UWB Wireless Communications Research Center (INHA UWB-ITRC), Inha University, 402-751, Incheon, Korea {zhweihua2000}@hotmail.com Abstract. For the extreme short duration of the baseband Impulse Ra- dio (IR) Ultra-Wideband (UWB) transmission waveforms, even small amounts of timing jitter can bring out considerable system performance degradation. Thus jitter performance evaluation and corresponding sup- pression methods are very important for UWB high rate transceiver. We analyzed the jitter distribution function in UWB systems, also a jitter suppression method is proposed by modification of template waveforms. Performance of our proposed waveforms and traditional template wave- forms are compared by analysis and simulation, and the results verify our jitter suppression method works.1 1 Introduction Ultra-wideband (UWB) is proposed as the primary candidate for the physical layer technology of next high speed short range wireless communication for per- sonal area networks (PAN) [1]. This radio technology is based on the radiation of waveforms formed by a sequence of very short, about nanosecond or below nanosecond, base band pulses [2]. The impulsive nature means that synchro- nization error (or jitter) influences the correlation of the received waveform and the template waveform generated in the receiver, thus deteriorates the system perform. Some past researches about this problem have been proposed: The effects of timing jitter on the bit error rate (BER) of UWB have been analyzed [3][4]. To suppressing this degradation system clock with higher stability is proposed which has the capability of precisely positioning the sub-nanosecond pulses with Gaussian distributed root-mean-squared (RMS) jitter of 10ps and within a 50ns time window [5].
    [Show full text]
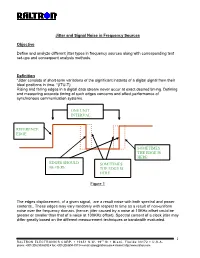
  • Jitter and Signal Noise in Frequency Sources
    Jitter and Signal Noise in Frequency Sources Objective Define and analyze different jitter types in frequency sources along with corresponding test set-ups and consequent analysis methods. Definition “Jitter consists of short-term variations of the significant instants of a digital signal from their ideal positions in time. “(ITU-T) Rising and falling edges in a digital data stream never occur at exact desired timing. Defining and measuring accurate timing of such edges concerns and affect performance of synchronous communication systems. ONE UNIT INTERVAL REFERENCE EDGE SOMETIMES THE EDGE IS HERE EDGES SHOULD SOMETIMES BE HERE THE EDGE IS HERE Figure 1 The edges displacement, of a given signal, are a result noise with both spectral and power contents.. These edges may vary randomly with respect to time as a result of non-uniform noise over the frequency domain. (hence; jitter caused by a noise at 10KHz offset could be greater or smaller than that of a noise at 100KHz offset). Spectral content of a clock jitter may differ greatly based on the different measurement techniques or bandwidth evaluated. 1 RALTRON ELECTRONICS CORP. ! 10651 N.W. 19th St ! Miami, Florida 33172 ! U.S.A. phone: +001(305) 593-6033 ! fax: +001(305)594-3973 ! e-mail: [email protected] ! internet: http://www.raltron.com System Disruptions caused by Jitter Clock recovery mechanisms, in network elements, are used to sample the digital signal using the recovered bit clock. If the digital signal and the clock have identical jitter, the constant jitter error will not affect the sampling instant and therefore no bit errors will arise.
    [Show full text]