DOCSLIB.ORG

The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

AN-1067 APPLICATION NOTE One Technology Way • P. O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: 781.329.4700 • Fax: 781.461.3113 • www.analog.com The Power Spectral Density of Phase Noise and Jitter: Theory, Data Analysis, and Experimental Results by Gil Engel INTRODUCTION GENERAL DESCRIPTION Jitter on analog-to-digital and digital-to-analog converter sam- There are numerous techniques for generating clocks used in pling clocks presents a limit to the maximum signal-to-noise electronic equipment. Circuits include R-C feedback circuits, ratio that can be achieved (see Integrated Analog-to-Digital and timers, oscillators, and crystals and crystal oscillators. Depend- Digital-to-Analog Converters by van de Plassche in the References ing on circuit requirements, less expensive sources with higher section). In this application note, phase noise and jitter are defined. phase noise (jitter) may be acceptable. However, recent devices The power spectral density of phase noise and jitter is developed, demand better clock performance and, consequently, more time domain and frequency domain measurement techniques costly clock sources. Similar demands are placed on the spectral are described, limitations of laboratory equipment are explained, purity of signals sampled by converters, especially frequency and correction factors to these techniques are provided. The synthesizers used as sources in the testing of current higher theory presented is supported with experimental results applied performance converters. In the following section, definitions to a real world problem. of phase noise and jitter are presented. Then a mathematical derivation is developed relating phase noise and jitter to their frequency representation. The frequency domain representations, or power spectral densities, are shown to directly provide a measure of phase noise/jitter. The theory developed is associated with analog-to-digital and digital-to-analog converters. A spectrum analyzer and an oscilloscope are used to measure a variety of signals. Finally, theory is coupled with experimental results applied to an AD9235 analog-to-digital converter (ADC). Rev. 0 | Page 1 of 20 AN-1067 Application Note TABLE OF CONTENTS Introduction ...................................................................................... 1 Test Equipment ............................................................................... 10 General Description ......................................................................... 1 Oscilloscopes ............................................................................... 10 Revision History ............................................................................... 2 Spectrum Analyzers ................................................................... 10 Definitions ......................................................................................... 3 Proof ............................................................................................. 11 Phase Noise ................................................................................... 3 Lab Results ....................................................................................... 12 Jitter ................................................................................................ 3 Signal 1 ......................................................................................... 12 Power Spectral Density .................................................................... 5 Signal 2 ......................................................................................... 12 Example 1 ...................................................................................... 6 Signal 3 ......................................................................................... 13 Example 2—Phase Noise ............................................................. 6 High Speed Converter ................................................................... 15 Example 3—Jitter .......................................................................... 7 Conclusion....................................................................................... 17 Application to Converters ............................................................... 8 References .................................................................................... 17 Example 1 ...................................................................................... 9 REVISION HISTORY 4/10—Revision 0: Initial Version Rev. 0 | Page 2 of 20 Application Note AN-1067 DEFINITIONS Phase noise and jitter have various interpretations. In the context The function Φ(t) can be composed of frequency components of this application note, phase noise and jitter are defined as not related to ωt, for example, thermal noise, shot noise, and 1/f follows: noise (flicker noise). However, in most cases, it is modeled as Consider the sinusoidal signal, Gaussian noise (see Frequency Synthesizers Theory and Design Third Edition by Manassewitsch in the References section). sin(ωt + A) (1) Similarly, a sample clock can be considered a periodic square where: wave with rising and falling edges repeating at a fixed time ω = 2πf. interval, τ, such that f is the desired frequency. A is a constant phase offset. τ = 1/f (3) 1.5 1.0 0.8 0.6 1.0 0.4 0.2 t) 0.5 ω 0 sin( –0.2 –0.4 0 –0.6 –0.8 –0.5 –1.0 0 0.5 1.0 1.5 2.0 0 /2 3 /2 2 PERIOD ( ) 0 ≤ ωt ≤ 2 08932-003 08932-001 Figure 3. Sampling Clock Figure 1. Normalized Sinusoidal Signal PHASE NOISE JITTER Phase noise is defined as an arbitrary function Φ(t) such that Jitter can be defined as an additive time variation Δ(t) to the Equation 1 becomes fixed interval τ, giving sin(ωt + A + Φ(t)) (2) τ + Δ(t) = 1/f + Δ(t) (4) 1.5 1.0 0.8 0.6 1.0 0.4 0.2 (t)) θ 0.5 t + 0 ω –0.2 sin( –0.4 0 –0.6 –0.8 –0.5 –1.0 0 0.5 1.0 1.5 2.0 0 /2 3 /2 2 PERIOD ( ) 0 ≤ ωt ≤ 2 08932-004 08932-002 Figure 4. Sampling Clock with Jitter Figure 2. Sinusoidal Signal with Phase Noise Likewise, Δ(t), is typically characterized as Gaussian noise. Rev. 0 | Page 3 of 20 AN-1067 Application Note 0 Noise analysis is straightforward above 5 kHz until the active –20 devices are limited at high frequency. Noise below 5 kHz exceeds –40 the shot noise and thermal noise. This noise varies inversely with frequency and is identified as 1/f noise. Figure 5 shows a –60 typical noise spectrum of an oscillator (see Manassewitsch in –80 the References section). –100 –120 NORMALIZED POWER(dB) –140 –160 –180 100 105 1010 1015 1020 FREQUENCY (MHz) 08932-005 Figure 5. Single-Sideband Noise Spectrum of an Oscillator Rev. 0 | Page 4 of 20 Application Note AN-1067 POWER SPECTRAL DENSITY Time domain signals have a direct relation to the frequency 1.0 domain through the Fourier transform (see Discrete-Time Signal 0.9 Processing by Oppenheim in the References section). The 0.8 Fourier transform can be viewed as the magnitude and phase 0.7 spectrum of a signal. A signal’s power can also be viewed in the 0.6 frequency domain. The power spectrum or power spectral 0.5 density is given by 0.4 Syy(ω) = Y(ω) × Y’(ω) (5) 0.3 where Y(ω) is the Fourier transform of y(t). POWER NORMALIZED TO 1 0.2 As stated previously in the Definitions section, Φ(t) can be any 0.1 arbitrary undesired signal. To simplify this analysis, Φ(t) is set 0 to a single frequency. Consider the following: 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 (Hz) × 104 08932-006 Φ(t) = θdsinωmt (6) Figure 6. Power Spectral Density, Syy(ω) Such that Equation 2 becomes Figure 6 is a plot of y(t) = sin(ωct + θdsinωmt) (7) Syy(ω) = Y(ω) × Y’(ω) The result is a phase-modulated signal, y(t), with maximum where Y(ω) is the Fourier Transform of y(t). phase deviation in radians, θd, at a frequency, fm, with ωm = 2πfm, and no offset, A = 0. Syy(ω) displays the magnitude of the power at the frequency, f. The power spectral density of the signal, y(t), modulated by a The Jacobi-Anger expansion (see Concise Encyclopedia of single frequency, fm, only has components at fc and fm with Mathematics by Weisstein in the References section) states that Bessel-squared magnitudes. iz cos( ) n in The higher order Bessel coefficients attenuate very quickly. A e i Jn () z e (8) n log power scale provides better dynamic range, showing the or higher order components in the same view as the large carrier component. The log of Syy(ω) is given by the following equation: e iz sin( ) J() z e in (9) n Lpy(ω) = 10log10(Syy(ω)) (13) n can be manipulated with the help of Euler’s identity to give and is shown in Figure 7. 0 cos(z sin ) J0 ( z ) 2 J2n ( z )cos(2 n ) (10) n1 –20 and –40 –60 sin(z sin ) 2 J2n 1 ( z )cos[(2 n 1) ] (11) n1 –80 (dB) where the Jn(z) factors are Bessel functions of the first kind. –100 Using trigonometric identities, Equation 7, Equation 10, and –120 Equation 11 can be manipulated to give –140 0 d c y(t) = J (θ )sin(ω t) –160 + J1(θd)[sin(ωc+ ωm)t – sin(ωc − ωm)t] 2.4 2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 2 d c m c m + J (θ )[sin(ω + 2ω )t – sin(ω − 2ω )t] (Hz) × 104 08932-007 + J3(θd)[sin(ωc+ 3ωm)t – sin(ωc − 3ωm)t] Figure 7. Log of Power Spectral Density, Syy(ω) + … (12) Additional terms are now clearly visible. As the phase deviation From Equation 12, it can be seen that y(t) has a first-order Bessel increases, the magnitude at the carrier frequency decreases and component at the carrier frequency, fc, and Bessel-weighted the magnitude of the modulation terms increases. 500 mrad of signals at multiples of the modulation frequency, fm, offset from phase deviation reduces the carrier
Recommended publications

  • Blind Denoising Autoencoder

    1 Blind Denoising Autoencoder Angshul Majumdar In recent times a handful of papers have been published on Abstract—The term ‘blind denoising’ refers to the fact that the autoencoders used for signal denoising [10-13]. These basis used for denoising is learnt from the noisy sample itself techniques learn the autoencoder model on a training set and during denoising. Dictionary learning and transform learning uses the trained model to denoise new test samples. Unlike the based formulations for blind denoising are well known. But there has been no autoencoder based solution for the said blind dictionary learning and transform learning based approaches, denoising approach. So far autoencoder based denoising the autoencoder based methods were not blind; they were not formulations have learnt the model on a separate training data learning the model from the signal at hand. and have used the learnt model to denoise test samples. Such a The main disadvantage of such an approach is that, one methodology fails when the test image (to denoise) is not of the never knows how good the learned autoencoder will same kind as the models learnt with. This will be first work, generalize on unseen data. In the aforesaid studies [10-13] where we learn the autoencoder from the noisy sample while denoising. Experimental results show that our proposed method training was performed on standard dataset of natural images performs better than dictionary learning (K-SVD), transform (image-net / CIFAR) and used to denoise natural images. Can learning, sparse stacked denoising autoencoder and the gold the learnt model be used to recover images from other standard BM3D algorithm.
  • Johnson Noise and Shot Noise: the Determination of the Boltzmann Constant, Absolute Zero Temperature and the Charge of the Electron

    Johnson Noise and Shot Noise: the Determination of the Boltzmann Constant, Absolute Zero Temperature and the Charge of the Electron

    Johnson Noise and Shot Noise: The Determination of the Boltzmann Constant, Absolute Zero Temperature and the Charge of the Electron MIT Department of Physics (Dated: September 3, 2013) In electronic measurements, one observes \signals," which must be distinctly above the \noise." Noise induced from outside sources may be reduced by shielding and proper \grounding." Less noise means greater sensitivity with signal/noise as the figure of merit. However, there exist fundamental sources of noise which no clever circuit can avoid. The intrinsic noise is a result of the thermal jitter of the charge carriers and the quantization of charge. The purpose of this experiment is to measure these two limiting electrical noises. From the measurements, values of the Boltzmann constant and the charge of the electron will be derived. PREPARATORY QUESTIONS By the end of the 19th century, the accumulated ev- idence from chemistry, crystallography, and the kinetic Please visit the Johnson and Shot Noise chapter on the theory of gases left little doubt about the validity of the 8.13x website at mitx.mit.edu to review the background atomic theory of matter. Nevertheless, there were still material for this experiment. Answer all questions found arguments against the atomic theory, stemming from a in the chapter. Work out the solutions in your laboratory lack of "direct" evidence for the reality of atoms. In fact, notebook; submit your answers on the web site. there was no precise measurement yet available of the quantitative relation between atoms and the objects of direct scientific experience such as weights, meter sticks, EXPERIMENT GOALS clocks, and ammeters.
  • A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers

    A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers

    Sensors 2011, 11, 9233-9241; doi:10.3390/s111009233 OPEN ACCESS sensors ISSN 1424-8220 www.mdpi.com/journal/sensors Article A Comparison of Delayed Self-Heterodyne Interference Measurement of Laser Linewidth Using Mach-Zehnder and Michelson Interferometers Albert Canagasabey 1,2,*, Andrew Michie 1,2, John Canning 1, John Holdsworth 3, Simon Fleming 2, Hsiao-Chuan Wang 1,2 and Mattias L. Åslund 1 1 Interdisciplinary Photonics Laboratories (iPL), School of Chemistry, University of Sydney, 2006, NSW, Australia; E-Mails: [email protected] (A.M.); [email protected] (J.C.); [email protected] (H.-C.W.); [email protected] (M.L.Å.) 2 Institute of Photonics and Optical Science (IPOS), School of Physics, University of Sydney, 2006, NSW, Australia; E-Mail: [email protected] (S.F.) 3 SMAPS, University of Newcastle, Callaghan, NSW 2308, Australia; E-Mail: [email protected] (J.H.) * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +61-2-9351-1984. Received: 17 August 2011; in revised form: 13 September 2011 / Accepted: 23 September 2011 / Published: 27 September 2011 Abstract: Linewidth measurements of a distributed feedback (DFB) fibre laser are made using delayed self heterodyne interferometry (DHSI) with both Mach-Zehnder and Michelson interferometer configurations. Voigt fitting is used to extract and compare the Lorentzian and Gaussian linewidths and associated sources of noise. The respective measurements are wL (MZI) = (1.6 ± 0.2) kHz and wL (MI) = (1.4 ± 0.1) kHz. The Michelson with Faraday rotator mirrors gives a slightly narrower linewidth with significantly reduced error.
  • Understanding Jitter and Wander Measurements and Standards Second Edition Contents

    Understanding Jitter and Wander Measurements and Standards Second Edition Contents

    Understanding Jitter and Wander Measurements and Standards Second Edition Contents Page Preface 1. Introduction to Jitter and Wander 1-1 2. Jitter Standards and Applications 2-1 3. Jitter Testing in the Optical Transport Network 3-1 (OTN) 4. Jitter Tolerance Measurements 4-1 5. Jitter Transfer Measurement 5-1 6. Accurate Measurement of Jitter Generation 6-1 7. How Tester Intrinsics and Transients 7-1 affect your Jitter Measurement 8. What 0.172 Doesn’t Tell You 8-1 9. Measuring 100 mUIp-p Jitter Generation with an 0.172 Tester? 9-1 10. Faster Jitter Testing with Simultaneous Filters 10-1 11. Verifying Jitter Generator Performance 11-1 12. An Overview of Wander Measurements 12-1 Acronyms Welcome to the second edition of Agilent Technologies Understanding Jitter and Wander Measurements and Standards booklet, the distillation of over 20 years’ experience and know-how in the field of telecommunications jitter testing. The Telecommunications Networks Test Division of Agilent Technologies (formerly Hewlett-Packard) in Scotland introduced the first jitter measurement instrument in 1982 for PDH rates up to E3 and DS3, followed by one of the first 140 Mb/s jitter testers in 1984. SONET/SDH jitter test capability followed in the 1990s, and recently Agilent introduced one of the first 10 Gb/s Optical Channel jitter test sets for measurements on the new ITU-T G.709 frame structure. Over the years, Agilent has been a significant participant in the development of jitter industry standards, with many contributions to ITU-T O.172/O.173, the standards for jitter test equipment, and Telcordia GR-253/ ITU-T G.783, the standards for operational SONET/SDH network equipment.
  • 10S Johnson-Nyquist Noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011)

    10S Johnson-Nyquist Noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011)

    Chapter 10S Johnson-Nyquist noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011) Johnson noise Johnson-Nyquist theorem Boltzmann constant Parseval relation Correlation function Spectral density Wiener-Khinchin (or Khintchine) Flicker noise Shot noise Poisson distribution Brownian motion Fluctuation-dissipation theorem Langevin function ___________________________________________________________________________ John Bertrand "Bert" Johnson (October 2, 1887–November 27, 1970) was a Swedish-born American electrical engineer and physicist. He first explained in detail a fundamental source of random interference with information traveling on wires. In 1928, while at Bell Telephone Laboratories he published the journal paper "Thermal Agitation of Electricity in Conductors". In telecommunication or other systems, thermal noise (or Johnson noise) is the noise generated by thermal agitation of electrons in a conductor. Johnson's papers showed a statistical fluctuation of electric charge occur in all electrical conductors, producing random variation of potential between the conductor ends (such as in vacuum tube amplifiers and thermocouples). Thermal noise power, per hertz, is equal throughout the frequency spectrum. Johnson deduced that thermal noise is intrinsic to all resistors and is not a sign of poor design or manufacture, although resistors may also have excess noise. http://en.wikipedia.org/wiki/John_B._Johnson 1 ____________________________________________________________________________ Harry Nyquist (February 7, 1889 – April 4, 1976) was an important contributor to information theory. http://en.wikipedia.org/wiki/Harry_Nyquist ___________________________________________________________________________ 10S.1 Histrory In 1926, experimental physicist John Johnson working in the physics division at Bell Labs was researching noise in electronic circuits. He discovered random fluctuations in the voltages across electrical resistors, whose power was proportional to temperature.
  • Measurement Techniques of Ultra-Wideband Transmissions

    Measurement Techniques of Ultra-Wideband Transmissions

    Rec. ITU-R SM.1754-0 1 RECOMMENDATION ITU-R SM.1754-0* Measurement techniques of ultra-wideband transmissions (2006) Scope Taking into account that there are two general measurement approaches (time domain and frequency domain) this Recommendation gives the appropriate techniques to be applied when measuring UWB transmissions. Keywords Ultra-wideband( UWB), international transmissions, short-duration pulse The ITU Radiocommunication Assembly, considering a) that intentional transmissions from devices using ultra-wideband (UWB) technology may extend over a very large frequency range; b) that devices using UWB technology are being developed with transmissions that span numerous radiocommunication service allocations; c) that UWB technology may be integrated into many wireless applications such as short- range indoor and outdoor communications, radar imaging, medical imaging, asset tracking, surveillance, vehicular radar and intelligent transportation; d) that a UWB transmission may be a sequence of short-duration pulses; e) that UWB transmissions may appear as noise-like, which may add to the difficulty of their measurement; f) that the measurements of UWB transmissions are different from those of conventional radiocommunication systems; g) that proper measurements and assessments of power spectral density are key issues to be addressed for any radiation, noting a) that terms and definitions for UWB technology and devices are given in Recommendation ITU-R SM.1755; b) that there are two general measurement approaches, time domain and frequency domain, with each having a particular set of advantages and disadvantages, recommends 1 that techniques described in Annex 1 to this Recommendation should be considered when measuring UWB transmissions. * Radiocommunication Study Group 1 made editorial amendments to this Recommendation in the years 2018 and 2019 in accordance with Resolution ITU-R 1.
  • Retrospective Analysis of Phonatory Outcomes After CO2 Laser Thyroarytenoid 00111 Myoneurectomy in Patients with Adductor Spasmodic Dysphonia

    Retrospective Analysis of Phonatory Outcomes After CO2 Laser Thyroarytenoid 00111 Myoneurectomy in Patients with Adductor Spasmodic Dysphonia

    Global Journal of Otolaryngology ISSN 2474-7556 Research Article Glob J Otolaryngol Volume 22 Issue 4- June 2020 Copyright © All rights are reserved by Rohan Bidaye DOI: 10.19080/GJO.2020.22.556091 Retrospective Analysis of Phonatory Outcomes after CO2 Laser Thyroarytenoid Myoneurectomy in Patients with Adductor Spasmodic Dysphonia Rohan Bidaye1*, Sachin Gandhi2*, Aishwarya M3 and Vrushali Desai4 1Senior Clinical Fellow in Laryngology, Deenanath Mangeshkar Hospital, India 2Head of Department of ENT, Deenanath Mangeshkar Hospital, India 3Fellow in Laryngology, Deenanath Mangeshkar Hospital, India 4Chief Consultant, Speech Language Pathologist, Deenanath Mangeshkar Hospital, India Submission: May 16, 2020; Published: June 08, 2020 *Corresponding author: Rohan Bidaye and Sachin Gandhi, Senior Clinical Fellow in Laryngology and Head of Department of ENT, Deenanath Mangeshkar Hospital, India Abstract Introduction: Adductor spasmodic dysphonia (ADSD) is a focal laryngeal dystonia characterized by spasms of laryngeal muscles during speech. Botulinum toxin injection in the Thyroarytenoid muscle remains the gold-standard treatment for ADSD. However, as Botulinum toxin CO2 laser Thyroarytenoid myoneurectomy (TAM) has been reported as an effective technique for treatment of ADSD. It provides sustained improvementinjections need in tothe be voice repeated over a periodically,longer duration. the voice quality fluctuates over a longer period. A Microlaryngoscopic Transoral approach to Methods: Trans oral Microlaryngoscopic CO2 laser TAM was performed in 14 patients (5 females and 9 males), aged between 19 and 64 years who were diagnosed with ADSD. Data was collected from over 3 years starting from Jan 2014 – Dec 2016. GRBAS scale along with Multi- dimensional voice programme (MDVP) analysis of the voice and Video laryngo-stroboscopic (VLS) samples at the end of 3 and 12 months of surgery would be compared with the pre-operative readings.
  • Arxiv:2003.13216V1 [Cs.CV] 30 Mar 2020

    Arxiv:2003.13216V1 [Cs.CV] 30 Mar 2020

    Learning to Learn Single Domain Generalization Fengchun Qiao Long Zhao Xi Peng University of Delaware Rutgers University University of Delaware [email protected] [email protected] [email protected] Abstract : Source domain(s) <latexit sha1_base64="glUSn7xz2m1yKGYjqzzX12DA3tk=">AAAB8nicjVDLSsNAFL3xWeur6tLNYBFclaQKdllw47KifUAaymQ6aYdOJmHmRiihn+HGhSJu/Rp3/o2TtgsVBQ8MHM65l3vmhKkUBl33w1lZXVvf2Cxtlbd3dvf2KweHHZNkmvE2S2SieyE1XArF2yhQ8l6qOY1Dybvh5Krwu/dcG5GoO5ymPIjpSIlIMIpW8vsxxTGjMr+dDSpVr+bOQf4mVViiNai894cJy2KukElqjO+5KQY51SiY5LNyPzM8pWxCR9y3VNGYmyCfR56RU6sMSZRo+xSSufp1I6exMdM4tJNFRPPTK8TfPD/DqBHkQqUZcsUWh6JMEkxI8X8yFJozlFNLKNPCZiVsTDVlaFsq/6+ETr3mndfqNxfVZmNZRwmO4QTOwINLaMI1tKANDBJ4gCd4dtB5dF6c18XoirPcOYJvcN4+AY5ZkWY=</latexit> <latexit sha1_base64="9X8JvFzvWSXuFK0x/Pe60//G3E4=">AAACD3icbVDLSsNAFJ3UV62vqks3g0Wpm5LW4mtVcOOyUvuANpTJZNIOnUzCzI1YQv/Ajb/ixoUibt26829M2iBqPTBwOOfeO/ceOxBcg2l+GpmFxaXllexqbm19Y3Mrv73T0n6oKGtSX/iqYxPNBJesCRwE6wSKEc8WrG2PLhO/fcuU5r68gXHALI8MJHc5JRBL/fxhzyMwpEREjQnuAbuD6AI3ptOx43uEy6I+muT6+YJZMqfA86SckgJKUe/nP3qOT0OPSaCCaN0tmwFYEVHAqWCTXC/ULCB0RAasG1NJPKataHrPBB/EioNdX8VPAp6qPzsi4mk99uy4Mtle//US8T+vG4J7ZkVcBiEwSWcfuaHA4OMkHOxwxSiIcUwIVTzeFdMhUYRCHOEshPMEJ98nz5NWpVQ+LlWvq4VaJY0ji/bQPiqiMjpFNXSF6qiJKLpHj+gZvRgPxpPxarzNSjNG2rOLfsF4/wJA4Zw6</latexit> S S : Target domain(s) <latexit sha1_base64="ssITTP/Vrn2uchq9aDxvcfruPQc=">AAACD3icbVDLSgNBEJz1bXxFPXoZDEq8hI2Kr5PgxWOEJAaSEHonnWTI7Owy0yuGJX/gxV/x4kERr169+TfuJkF8FTQUVd10d3mhkpZc98OZmp6ZnZtfWMwsLa+srmXXN6o2iIzAighUYGoeWFRSY4UkKayFBsH3FF57/YvUv75BY2WgyzQIselDV8uOFECJ1MruNnygngAVl4e8QXhL8Rkvg+ki8Xbgg9R5uzfMtLI5t+COwP+S4oTk2ASlVva90Q5E5KMmocDaetENqRmDISkUDjONyGIIog9drCdUg4+2GY/+GfKdRGnzTmCS0sRH6veJGHxrB76XdKbX299eKv7n1SPqnDRjqcOIUIvxok6kOAU8DYe3pUFBapAQEEYmt3LRAwOCkgjHIZymOPp6+S+p7heKB4XDq8Pc+f4kjgW2xbZZnhXZMTtnl6zEKkywO/bAntizc+88Oi/O67h1ypnMbLIfcN4+ATKRnDE=</latexit>
  • Next Topic: NOISE

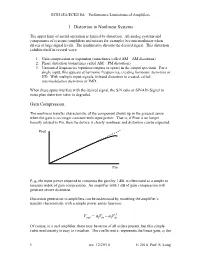
    Next Topic: NOISE

    ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize.
  • Thermal-Noise.Pdf

    Thermal-Noise.Pdf

    Thermal Noise Introduction One might naively believe that if all sources of electrical power are removed from a circuit that there will be no voltage across any of the components, a resistor for example. On average this is correct but a close look at the rms voltage would reveal that a "noise" voltage is present. This intrinsic noise is due to thermal fluctuations and can be calculated as may be done in your second year thermal physics course! The main goal of this experiment is to measure and characterize this noise: Johnson noise. In order to measure the intrinsic noise of a component one must first reduce the extrinsic sources of noise, i.e. interference. You have probably noticed that if you touch the input lead to an oscilloscope a large signal appears. Try this now and characterize the signal you see. Note that you are acting as an antenna! Make sure you look at both long time scales, say 10 ms, and shorter time scales, say 1 s. What are the likely sources of the signals you see? You may recall seeing this before in the First Year Laboratory. This interference is characterized by two features. First, the noise voltage is characterized by a spectrum, i.e. the noise voltage Vn ( f ) is a function of frequency. 2 Since noise usually has a time average of zero, the power spectrum Vn ( f ) is specified in each frequency interval df . Second, the measuring instrument is also characterized by a spectral response or bandwidth. In our case the bandwidth of the oscilloscope is from fL =0 (when input is DC coupled) to an upper frequency fH usually noted on the scope (beware of bandwidth limiting switches).
  • Estimation from Quantized Gaussian Measurements: When and How to Use Dither Joshua Rapp, Robin M

    Estimation from Quantized Gaussian Measurements: When and How to Use Dither Joshua Rapp, Robin M

    1 Estimation from Quantized Gaussian Measurements: When and How to Use Dither Joshua Rapp, Robin M. A. Dawson, and Vivek K Goyal Abstract—Subtractive dither is a powerful method for remov- be arbitrarily far from minimizing the mean-squared error ing the signal dependence of quantization noise for coarsely- (MSE). For example, when the population variance vanishes, quantized signals. However, estimation from dithered measure- the sample mean estimator has MSE inversely proportional ments often naively applies the sample mean or midrange, even to the number of samples, whereas the MSE achieved by the when the total noise is not well described with a Gaussian or midrange estimator is inversely proportional to the square of uniform distribution. We show that the generalized Gaussian dis- the number of samples [2]. tribution approximately describes subtractively-dithered, quan- tized samples of a Gaussian signal. Furthermore, a generalized In this paper, we develop estimators for cases where the Gaussian fit leads to simple estimators based on order statistics quantization is neither extremely fine nor extremely coarse. that match the performance of more complicated maximum like- The motivation for this work stemmed from a series of lihood estimators requiring iterative solvers. The order statistics- experiments performed by the authors and colleagues with based estimators outperform both the sample mean and midrange single-photon lidar. In [3], temporally spreading a narrow for nontrivial sums of Gaussian and uniform noise. Additional laser pulse, equivalent to adding non-subtractive Gaussian analysis of the generalized Gaussian approximation yields rules dither, was found to reduce the effects of the detector’s coarse of thumb for determining when and how to apply dither to temporal resolution on ranging accuracy.
  • Image Denoising by Autoencoder: Learning Core Representations

    Image Denoising by Autoencoder: Learning Core Representations

    Image Denoising by AutoEncoder: Learning Core Representations Zhenyu Zhao College of Engineering and Computer Science, The Australian National University, Australia, [email protected] Abstract. In this paper, we implement an image denoising method which can be generally used in all kinds of noisy images. We achieve denoising process by adding Gaussian noise to raw images and then feed them into AutoEncoder to learn its core representations(raw images itself or high-level representations).We use pre- trained classifier to test the quality of the representations with the classification accuracy. Our result shows that in task-specific classification neuron networks, the performance of the network with noisy input images is far below the preprocessing images that using denoising AutoEncoder. In the meanwhile, our experiments also show that the preprocessed images can achieve compatible result with the noiseless input images. Keywords: Image Denoising, Image Representations, Neuron Networks, Deep Learning, AutoEncoder. 1 Introduction 1.1 Image Denoising Image is the object that stores and reflects visual perception. Images are also important information carriers today. Acquisition channel and artificial editing are the two main ways that corrupt observed images. The goal of image restoration techniques [1] is to restore the original image from a noisy observation of it. Image denoising is common image restoration problems that are useful by to many industrial and scientific applications. Image denoising prob- lems arise when an image is corrupted by additive white Gaussian noise which is common result of many acquisition channels. The white Gaussian noise can be harmful to many image applications. Hence, it is of great importance to remove Gaussian noise from images.