Inland and Coastal Navigation Workbook
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Marine Charts and Navigation
OceanographyLaboratory Name Lab Exercise#2 MARINECHARTS AND NAVIGATION DEFINITIONS: Bearing:The directionto a target from your vessel, expressedin degrees, 0OO" clockwise through 360". Bearingcan be expressedas a true bearing (in degreesfrom true, or geographicnorth), a magneticbearing (in degreesfrom magnetic north),or a relativebearing (in degreesfrom ship's head). Gourse:The directiona ship must travel to arrive at a desireddestination. Cursor:A cross hairmark on the radarscreen operated by the trackball.The cursor is used to measurea target'srange and bearing,set the guard zone,and plot the movementof other ships. ElectronicBearing Line (EBLI: A line on the radar screenthat indicates the bearing to a target. Fix: The charted positionof a vesselor radartarget. Heading:The directionin which a ship's bow pointsor headsat any instant, expressedin degrees,O0Oo clockwise through 360o,from true or magnetic north. The headingof a ship is alsocalled "ship's head". Knot: The unit of speedused at sea. lt is equivalentto one nauticalmile perhour. Latitude:The angulardistance north or south of the equatormeasured from O" at the Equatorto 9Ooat the poles.For most navigationalpurposes, one degree of latitudeis assumedto be equalto 60 nauticalmiles. Thus, one minute of latitude is equalto one nauticalmile. Longitude:The'angular distance on the earth measuredfrom the Prime Meridian (O') at Greenwich,England east or west through 180'. Every 15 degreesof longitudeeast or west of the PrimeMeridian is equalto one hour's difference from GreenwichMean Time (GMT)or Universal (UT). Time NauticalMile: The basic unit of distanceat sea, equivalentto 6076 feet, 1.85 kilometers,or 1.15 statutemiles. Pip:The imageof a targetecho displayedon the radarscreen; also calleda "blip". -

Angles, Azimuths and Bearings
Surveying & Measurement Angles, Azimuths and Bearings Introduction • Finding the locations of points and orientations of lines depends on measurements of angles and directions. • In surveying, directions are given by azimuths and bearings. • Angels measured in surveying are classified as . Horizontal angels . Vertical angles Introduction • Total station instruments are used to measure angels in the field. • Three basic requirements determining an angle: . Reference or starting line, . Direction of turning, and . Angular distance (value of the angel) Units of Angel Measurement In the United States and many other countries: . The sexagesimal system: degrees, minutes, and seconds with the last unit further divided decimally. (The circumference of circles is divided into 360 parts of degrees; each degree is further divided into minutes and seconds) • In Europe . Centesimal system: The circumference of circles is divided into 400 parts called gon (previously called grads) Units of Angel Measurement • Digital computers . Radians in computations: There are 2π radians in a circle (1 radian = 57.30°) • Mil - The circumference of a circle is divided into 6400 parts (used in military science) Kinds of Horizontal Angles • The most commonly measured horizontal angles in surveying: . Interior angles, . Angles to the right, and . Deflection angles • Because they differ considerably, the kind used must be clearly identified in field notes. Interior Angles • It is measured on the inside of a closed polygon (traverse) or open as for a highway. • Polygon: closed traverse used for boundary survey. • A check can be made because the sum of all angles in any polygon must equal • (n-2)180° where n is the number of angles. -
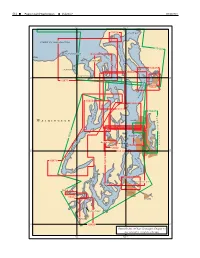
Chapter 13 -- Puget Sound, Washington
514 Puget Sound, Washington Volume 7 WK50/2011 123° 122°30' 18428 SKAGIT BAY STRAIT OF JUAN DE FUCA S A R A T O 18423 G A D A M DUNGENESS BAY I P 18464 R A A L S T S Y A G Port Townsend I E N L E T 18443 SEQUIM BAY 18473 DISCOVERY BAY 48° 48° 18471 D Everett N U O S 18444 N O I S S E S S O P 18458 18446 Y 18477 A 18447 B B L O A B K A Seattle W E D W A S H I N ELLIOTT BAY G 18445 T O L Bremerton Port Orchard N A N 18450 A 18452 C 47° 47° 30' 18449 30' D O O E A H S 18476 T P 18474 A S S A G E T E L N 18453 I E S C COMMENCEMENT BAY A A C R R I N L E Shelton T Tacoma 18457 Puyallup BUDD INLET Olympia 47° 18456 47° General Index of Chart Coverage in Chapter 13 (see catalog for complete coverage) 123° 122°30' WK50/2011 Chapter 13 Puget Sound, Washington 515 Puget Sound, Washington (1) This chapter describes Puget Sound and its nu- (6) Other services offered by the Marine Exchange in- merous inlets, bays, and passages, and the waters of clude a daily newsletter about future marine traffic in Hood Canal, Lake Union, and Lake Washington. Also the Puget Sound area, communication services, and a discussed are the ports of Seattle, Tacoma, Everett, and variety of coordinative and statistical information. -

Using the Suunto Hand Bearing Compass
R Application Note Using the Suunto Hand Bearing Compass Overview The Suunto bearing compass is used to measure an object’s bearing angle relative to magnetic North. The compass has a second scale for reading bearing angle from South. It is designed for viewing an object and its bearing angle simultaneously. This application note outlines the basic steps for using the Suunto bearing compass. Taking a Bearing 1. Site distant object. Use one eye to view distant object and the other to Figure 1: A Suunto Bearing Compass look into compass. With both eyes open, visually align vertical marker inside compass to distant object. Figure 2: Sighting an object Figure 3: Aligning compass sight and distant object 2. Take a reading. Every ten-degree marker is labeled with two numbers. The bottom number indicates degrees from magnetic North in a clockwise direction. The top number indicates degrees from magnetic South in a clockwise direction. Figure 4: Composite view through compass sight. The building edge is 275° from magnetic North. 3. Account for difference between true North and magnetic North. The compass points to magnetic North. The orientation of an object is measured in degrees East from North. The orientation of an object in San Francisco (and in the Bay Area) to true North is the compass reading from magnetic north plus 15°. The building edge in Figure 4 is 275° from Magnetic North. Therefore, the building edge in Figure 4 is 290° (275° + 15°) from true North. Visit one of the websites below for the magnetic declination for other locations. -

Black on Monmonier, 'Rhumb Lines and Map Wars: a Social History of the Mercator Projection'
H-HistGeog Black on Monmonier, 'Rhumb Lines and Map Wars: A Social History of the Mercator Projection' Review published on Friday, October 1, 2004 Mark Monmonier. Rhumb Lines and Map Wars: A Social History of the Mercator Projection. Chicago: University of Chicago Press, 2004. xiv + 242 pp. $25.00 (cloth), ISBN 978-0-226-53431-2. Reviewed by Jeremy Black (Department of History, Exeter University)Published on H-HistGeog (October, 2004) Monmonier, Distinguished Professor of Geography at Syracuse University, offers yet another first- rate contribution to the literature on cartography. His focus is one of the most famous projections, that of Gerard Mercator. As Monmonier points out, the popularity of this projection reflected its value for sailors, not least the map's value for plotting an easily followed course that could be marked off with a straight-edge and readily converted to a bearing. Mercator sought to reconcile the navigator's need for a straightforward course with the trade-offs inherent in flattening a globe. Mercator's projection affords negligible distortion on large-scale detailed maps of small areas, but relative size is markedly misrepresented on Mercator charts because of the increased poleward separation of parallels required to straighten out loxodromes. Monmonier shows how the projection was subsequently employed. It became the cartographic expression of what he terms a hot idea in the late 1590s, when Jodocus Hondius and Edward Wright offered their own versions of Mercator's world. Hondius relied heavily on Wright, who developed a mathematical description as well as tables showing how to position the parallels. Monmonier then takes the story forward showing how different demands, for example for artillery aiming, influenced the use of projections. -
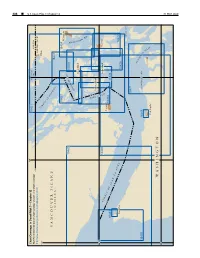
CPB7 C12 WEB.Pdf
488 ¢ U.S. Coast Pilot 7, Chapter 12 Chapter 7, Pilot Coast U.S. 124° 123° Chart Coverage in Coast Pilot 7—Chapter 12 18421 BOUNDARY NOAA’s Online Interactive Chart Catalog has complete chart coverage BAY CANADA 49° http://www.charts.noaa.gov/InteractiveCatalog/nrnc.shtml UNITED STATES S T R Blaine 125° A I T O F G E O R V ANCOUVER ISLAND G (CANADA) I A 18431 18432 18424 Bellingham A S S Y P B 18460 A R 18430 E N D L U L O I B N G Orcas Island H A M B A Y H A R O San Juan Island S T 48°30' R A S I Lopez Island Anacortes T 18465 T R A I Victoria T O F 18433 18484 J 18434 U A N D E F U C Neah Bay A 18427 18429 SKAGIT BAY 18471 A D M I R A L DUNGENESS BAY T 18485 18468 Y I N Port Townsend L E T Port Angeles W ASHINGTON 48° 31 MAY 2020 31 MAY 31 MAY 2020 U.S. Coast Pilot 7, Chapter 12 ¢ 489 Strait of Juan De Fuca and Georgia, Washington (1) thick weather, because of strong and irregular currents, ENC - extreme caution and vigilance must be exercised. Chart - 18400 Navigators not familiar with these waters should take a pilot. (2) This chapter includes the Strait of Juan de Fuca, (7) Sequim Bay, Port Discovery, the San Juan Islands and COLREGS Demarcation Lines its various passages and straits, Deception Pass, Fidalgo (8) The International Regulations for Preventing Island, Skagit and Similk Bays, Swinomish Channel, Collisions at Sea, 1972 (72 COLREGS) apply on all the Fidalgo, Padilla, and Bellingham Bays, Lummi Bay, waters of the Strait of Juan de Fuca, Haro Strait, and Strait Semiahmoo Bay and Drayton Harbor and the Strait of of Georgia. -

Math for Surveyors
Math For Surveyors James A. Coan Sr. PLS Topics Covered 1) The Right Triangle 2) Oblique Triangles 3) Azimuths, Angles, & Bearings 4) Coordinate geometry (COGO) 5) Law of Sines 6) Bearing, Bearing Intersections 7) Bearing, Distance Intersections Topics Covered 8) Law of Cosines 9) Distance, Distance Intersections 10) Interpolation 11) The Compass Rule 12) Horizontal Curves 13) Grades and Slopes 14) The Intersection of two grades 15) Vertical Curves The Right Triangle B Side Opposite (a) A C Side Adjacent (b) a b a SineA = CosA = TanA = c c b c c b CscA = SecA = CotA = a b a The Right Triangle The above trigonometric formulas Can be manipulated using Algebra To find any other unknowns The Right Triangle Example: a a SinA = SinA· c = a = c c SinA b b CosA = CosA· c = b = c c CosA a a TanA = TanA·b = a = b b TanA Oblique Triangles An oblique triangle is one that does not contain a right angle Oblique Triangles This type of triangle can be solved using two additional formulas Oblique Triangles The Law of Sines a b c = = Sin A Sin B Sin C C b a A c B Oblique Triangles The law of Cosines a2 = b2 + c2 - 2bc Cos A C b a A c B Oblique Triangles When solving this kind of triangle we can sometimes get two solutions, one solution, or no solution. Oblique Triangles When angle A is obtuse (more than 90°) and side a is shorter than or equal to side c, there is no solution. C b a B A c Oblique Triangles When angle A is obtuse and side a is greater than side c then side a can only intersect side b in one place and there is only one solution. -

Nautical Charts
7DOCUBENT RESUME ,Ar ED 125 934 ,_ SONI 160 AUTBOR tcCallum, W. F.; Botly, D. B. TITLE Eautical.Charts: Another Dimension in Developing Map Skills. Instructional Activities Series IA/S-11. INSTITUTION National Council for Geographic Education. PUB DATE (75) NOTE, 2Cp.; For related documents, see ED 096 235 and SO 1 009 140-167 AVAILABLE ?RCM NCGE Central Office, 115 North Marion Street, Oak Park, Illinois 60301 ($1.00, secondary set $15.25) EDRS PRICE 8F-$0.83 Plus Postage. BC Not Available from EDRS. DESCRIPTORS *Classroom Techniques; earth SIence; *Geography Instruction; Illustrations; Knowledge Level; Learning Lctivities; saps; *tap Skills; *Navigation; Oceanokogy; Physical Environment; Physical Geography; Seconda ry Education; *Simulation; Skill Development; Social Studies; Teaching Methods;-, Visual Aids ABSTPACT These activities are part of a series of 17 teacher- developed instructional activities for geography at the secondary-grade level described in SO 009 140. In theactivities students develop map skills by learning about and using nautical . charts. The first activity involves stUdents in using parallelrulers and a compass rose to find their hearings. Their ship, Prince Edward, . lies in an anchorage. They must take a bearing of eight otherships and record these bearings in the deck log. In the second activity students use dividers and the latitucle scale to peasure distance. During the class project they lay out courses to.steer and distances to run to bring their ship from one designated position itoanother. In the third activity students learn to interprettle common symbols found on a nautical chart by responding to discussion question g. Activity four is a simulation exercise in which students apply'the skills learned and the knowledge gained'in the first three exerises %by using z-namtical c4a-st- to move their ship from Passage Island to Thunder Bay. -

Working with Compass Bearings on a Topographic
IMPORTANT: Please refer to the Preface for Topographic Map Activities for preliminary instructions and information common to all Topographic Map Activities in the series. Topographic Map Activity 12 - Working with Compass Bearings (Revision 08-09-20) Objective: To enhance the sense of direction by working with compass bearings. Background: We have all heard someone exclaim “I need to get my bearings!” They usually mean that they are not certain, at the moment, of directions (north, south, east, and west). Fortunately, we usually move around on streets, sometimes trails, dotted with signs showing us the way. However, when we are on unfamiliar ground without such signs we need some tools to find direction. One tool is the sun, which rises in the east and sets in the west (but that could vary from 045° to 135° for sunrise and 225° to 315° for sunset, depending on the location on earth and the day of the year). There is moon rise and set (with similar issues). Also, there is the North Star, Polaris (if it’s not cloudy). Another tool is the Topo Maps. The right and left sides of each map are on lines of longitude going through both poles, so, they indicate true north (0°) and true south (180°). The top and bottom sides of each map are on lines of latitude that are parallel to the equator, so, they indicate true east (90°) and true west (270°). A magnetic compass is another tool, and it can be used together with a Topo Map, however, it points to the magnetic pole and not the North Pole (The difference is called declination and must be corrected for. -

Geomagnetism Student Guide.Pdf
Geomagnetism in the MESA Classroom: An Essential Science for Modern Society Student Guide NAME: _____________________________________ Image source: Earth science: Geomagnetic reversals David Gubbins, Nature 452, 165-167(13 March 2008), doi:10.1038/452165a MESA Program Prepared by Susan Buhr, Emily Kellagher and Susan Lynds Cooperative Institute for Research in Environmental Sciences (CIRES) University of Colorado CIRES Education Outreach http://cires.colorado.edu/education/outreach/ 1 TABLE OF CONTENTS Overview 4 Session One—Geomagnetism and Declination Handout 1.1--Earth’s Magnetic Field 6 Handout 1.2--Earth’s Magnetic Field and a Bar Magnet 8 Handout 1.3--Magnetic Declination 10 Handout 1.4--Magnetic Field Changes Over Time 14 Handout 1.5--Finding Magnetic Declination for a Location 18 Handout 1.6—Airport Runway Declination 22 Session Two—Course-Setting and Following Handout 2.1--Using a Compass to Navigate 30 Handout 2.2—Bearing Compass Use 32 Handout 2.3—Creating a Navigation Map to a Cache 36 Handout 2.4—Navigation with 1823 Pirate Map 40 Session Three—Solar Activity and the Earth’s Magnetic Field Handout 3.1—Aurora and Earth’s Magnetic Field 44 Handout 3.2—Introduction to Space Weather 48 Handout 3.3—Tracking Aurora 52 Handout 3.4—Space Weather Prediction Center 56 Session Four—Field Trip to Boulder to NOAA’s David Skaggs Research Center Handout 4.1—Field Trip Activity—What’s Going On Here? 58 Glossary 62 Related Apps and Recourses 64 CIRES Education Outreach http://cires.colorado.edu/education/outreach/ 2 CIRES Education Outreach http://cires.colorado.edu/education/outreach/ 3 OVERVIEW Overview: The Cooperative Institute for Research in Environmental Sciences (CIRES) Education Outreach’s GeoMag kit is a four-part after-school module that explores geomagnetism with compasses, navigation exercises, and a geo-caching activity, followed by a field trip to the National Oceanic and Atmospheric Administration’s David Skaggs Research Center in Boulder. -

Plotting a Bearing Onto Your Map
Plotting a Bearing onto your map • Why we plot bearings • Where am I? • Location by resectioning • Where is the ____ I can see in the distance? • Location by intersection • Using straight line course legs Location by Resectioning! a.k.a Triangulation N 70° ? ? A single bearing, sighted to a peak, resulting in two possible locations along a trail. Location by Resectioning N N 70° X 305° A bearing to a second peak confirms the location on the trail. Location by intersection Using bearings sighted from two or more known locations, to find an unknown location. An example ? ? GN MN 5° Where are we along the shoreline? Where is the cave we can see across the lake? We sight a bearing to a known cabin on the map, with a result of 60° M It’s NE of our location. 350 0 340 360 10 330 20 30 320 40 310 50 300 60 290 70 280 80 270 90 260 100 GN 250 110 MN 120 Center your protractor on the known240 location. 5° 130 230 140 220 150 160 210 170 200 190 180 350 0 340 360 10 330 20 30 320 40 310 50 300 60 290 70 280 80 270 90 260 100 110 250 120 240 130 230 140 220 150 160 210 170 200 190 180 GN MN 5° Align the protractor with Grid North. Our bearing was sighted relative to Magnetic North.! We want to plot it relative to Grid North.! We need to convert it. Bearing to plot on the map measured from GN MN Grid North 60M° + 5° = 65G° 65° 5° 60° Bearing measured with our compass from Magnetic North 350 0 340 360 10 330 20 30 320 40 310 50 65° 300 60 290 70 280 80 270 90 260 100 110 250 120 240 130 230 140 220 150 160 210 170 200 190 180 GN MN 5° Mark the converted bearing at the edge of the protractor. -

U.S. Coast Guard Historian's Office
U.S. Coast Guard Historian’s Office Preserving Our History For Future Generations Historic Light Station Information WASHINGTON ADMIRALTY HEAD LIGHT Location: STRAITS OF JUAN DE FUCA/PUGET SOUND; NEAR COUPEVILLE, FORT CASEY STATE PARK Station Established: 1860 Year Current Tower(s) First Lit: 1903 Operational? NO Automated? NO Deactivated: 1922 Foundation Materials: SURFACE Construction Materials: BRICK AND STUCCO Tower Shape: CONICAL Height: 120-feet Markings/Pattern: WHITE BRICK TOWER W/BLACK LANTERN Characteristics: Spanish-style structure, 2-story residence Relationship to Other Structure: ATTACHED Original Lens: FOURTH ORDER, FRESNEL 1903 Foghorn: Historical Information: The original lighthouse as completed during the months just prior to the Civil War and was among the West's earliest navigational aids. It had a fourth order Fresnel lens, and the light could be seen sixteen miles away. This light welcomed Puget Sound marine traffic to Admiralty Inlet. During the Spanish-American War, the US Army demolished the old lighthouse to build a fort (Fort Casey). The present lighthouse went into service in 1903 but was discontinued in 1927. It has been restored and now serves as a museum. It is only open during the summer for visitors. ALKI POINT LIGHT Page 1 of 12 U.S. Coast Guard Historian’s Office Preserving Our History For Future Generations Location: ELLIOTT BAY/PUGET SOUND Station Established: 1887 Year Current Tower(s) First Lit: 1913 Operational? YES Automated? YES 1984 Deactivated: n/a Foundation Materials: CONCRETE Construction Materials: MASONRY Tower Shape: OCTAGONAL ATTACHED TO SIGNAL BLDG Markings/Pattern: WHITE W/RED & BLACK TRIM Relationship to Other Structure: ATTACHED Original Lens: FOURTH ORDER FRESNEL 1913 BROWNS POINT LIGHT Location: COMMENCEMENT BAY E.