An Empirical Study of Observational Learning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Internet Peer-To-Peer File Sharing Policy Effective Date 8T20t2010
Title: Internet Peer-to-Peer File Sharing Policy Policy Number 2010-002 TopicalArea: Security Document Type Program Policy Pages: 3 Effective Date 8t20t2010 POC for Changes Director, Office of Computing and Information Services (OCIS) Synopsis Establishes a Dalton State College-wide policy regarding copyright infringement. Overview The popularity of Internet peer-to-peer file sharing is often the source of network resource allocation problems and copyright infringement. Purpose This policy will define Internet peer-to-peer file sharing and state the policy of Dalton State College (DSC) on this issue. Scope The scope of this policy includes all DSC computing resources. Policy Internet peer-to-peer file sharing applications are frequently used to distribute copyrighted materials such as music, motion pictures, and computer software. Such exchanges are illegal and are not permifted on Dalton State Gollege computers or network. See the standards outlined in the Appropriate Use Policy. DSG Procedures and Sanctions Failure to comply with the appropriate use of these resources threatens the atmosphere for the sharing of information, the free exchange of ideas, and the secure environment for creating and maintaining information property, and subjects one to discipline. Any user of any DSC system found using lT resources for unethical and/or inappropriate practices has violated this policy and is subject to disciplinary proceedings including suspension of DSC privileges, expulsion from school, termination of employment and/or legal action as may be appropriate. Although all users of DSC's lT resources have an expectation of privacy, their right to privacy may be superseded by DSC's requirement to protect the integrity of its lT resources, the rights of all users and the property of DSC and the State. -
Page Ranking Advogato Free and Open So
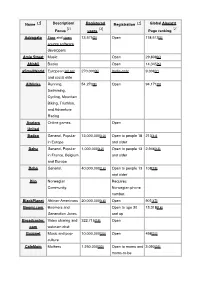
Name Description/ Registered Registration Global Alexa[1] Focus users Page ranking Advogato Free and open 13,575[2] Open 118,513[3] source software developers Amie Street Music Open 29,808[4] ANobii Books Open 14,345[5] aSmallWorld European jet set 270,000[6] Invite-only 9,306[7] and social elite Athlinks Running, 54,270[8] Open 94,171[9] Swimming, Cycling, Mountain Biking, Triathlon, and Adventure Racing Avatars Online games. Open United Badoo General, Popular 13,000,000[10] Open to people 18 213[11] in Europe and older Bahu General, Popular 1,000,000[12] Open to people 13 2,946[13] in France, Belgium and older and Europe Bebo General. 40,000,000[14] Open to people 13 108[15] and older Biip Norwegian Requires Community. Norwegian phone number. BlackPlanet African-Americans 20,000,000[16] Open 901[17] Boomj.com Boomers and Open to age 30 15,318[18] Generation Jones and up Broadcaster. Video sharing and 322,715[19] Open com webcam chat Buzznet Music and pop- 10,000,000[20] Open 498[21] culture CafeMom Mothers 1,250,000[22] Open to moms and 3,090[23] moms-to-be Cake Investing Open Financial Care2 Green living and 9,961,947[24] Open social activism Classmates.c School, college, 50,000,000[25] Open 923[26] om work and the military Cloob General. Popular Open in Iran. College College students. requires an e-mail Tonight address with an ".edu" ending CouchSurfin Worldwide network 871,049[27] Open g for making connections between travelers and the local communities they visit. -

Download a Copy of This Ebook At
Jesse Torres is President and Chief Operating Officer of Security Savings Bank in Henderson, Nevada. He is a regular speaker at banking industry conferences and seminars, he serves on the West Coast Anti-Money Laundering Forum and is a former Chairman of the Los Angeles Junior Chamber of Commerce. Prior to joining Security Savings Bank, he was a regulator with the Office of the Comptroller of the Currency (OCC), a Senior Consultant with KPMG Peat Marwick and a senior officer at several banks in the Los Angeles area. He is a graduate of UCLA and the Pacific Coast Banking School at the University of Washington. Jesse can be reached by e-mail at [email protected]. He can also be found on LinkedIn at www.linkedin.com/in/jessetorres. Join the conversation and become a fan on Facebook by searching Community Banker’s Guide to Social Network Marketing. Download a copy of this ebook at www.JesseTorres.com/cbgsnm/cbgsnm.pdf. Comments, corrections and other feedback may be sent to the author at [email protected]. © 2008 Jesse Torres Unauthorized duplication of this material is a violation of copyright. V20081201 Community Banker’s Guide to Social Network Marketing i TABLE OF CONTENTS EXECUTIVE SUMMARY ................................................................................................ 1 CHAPTER ONE – THE SOCIAL NETWORK ................................................................. 6 CHAPTER TWO – SOCIAL MEDIA.............................................................................. 16 CHAPTER THREE – SOCIAL NETWORK -

Public Index of Apple Inc. Exhibits
Public Index of Apple Inc. Exhibits EX. NO. DESCRIPTION BEG BATES END BATES Introducing Apple Music - All the Ways you Love Music. All in One Placce, Apple, http://www.apple.com/pr/library/2015/06/08Introducing-Apple-Music-All- APL-001 APL-PHONO_00000412 APL-PHONO_00000413 The-Ways-You-Love-Music-All-in-One-Place-.html, June 8, 2015, accessed August 5, 2015 APL-002 Report: RESTRICTED — Subject APL-PHONO_00004285 APL-PHONO_00004285 Agreement:t P RESTRICTED O —i Subject to Protective Order in Docket No. APL-003 16-CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00005380 APL-PHONO_00005386 Agreement: RESTRICTED — Subject to Protective Order in Docket APL-004 No. 16-CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00005387 APL-PHONO_00005387 Agreement: RESTRICTED — Subject to Protective Order in Docket APL-005 No. 16-CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00005388 APL-PHONO_00005398 Agreement: RESTRICTED — Subject to Protective Order in Docket No. 16- APL-006 CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00005399 APL-PHONO_00005404 Spreadsheet:RESTRICTED — Subject to Protective Order in APL-007 Docket No. 16-CRB-0001-PR (2018-2022) APL-PHONO_00006828 APL-PHONO_00006828 Spreadsheet:RESTRICTED(Ph d —III) Subject to Protective Order in Docket APL-008 No. 16-CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00008620 APL-PHONO_00008623 Spreadsheet:RESTRICTED — Subject to Protective Order in Docket APL-009 No. 16-CRB-0001-PR (2018-2022) (Phonorecords III) APL-PHONO_00008624 APL-PHONO_00008626 Report: News and Notes -

Entering New Markets and Diversifying Business the Role of Amazon’S Acquisitions in International Growth and Development
No. 69 – August 2019 Entering New Markets and Diversifying Business The Role of Amazon’s Acquisitions in International Growth and Development Stefan Schmid Sebastian Baldermann No. 69 – August 2019 Entering New Markets and Diversifying Business The Role of Amazon’s Acquisitions in International Growth and Development Stefan Schmid Sebastian Baldermann AUTHORS Prof. Dr. Stefan Schmid Chair of International Management and Strategic Management ESCP Europe Business School Berlin Heubnerweg 8-10, 14059 Berlin Germany T: +49 (0) 30 / 3 20 07-136 F: +49 (0) 30 / 3 20 07-107 [email protected] Sebastian Baldermann, M.A. ISSN: 1869-5426 Department of International Management and Strategic Management EDITOR ESCP Europe Business School Berlin © ESCP Europe Wirtschaftshochschule Berlin Heubnerweg 8-10, 14059 Berlin Heubnerweg 8-10, 14059 Berlin, Germany Germany T: +49 (0) 30 / 3 20 07-0 T: +49 (0) 30 / 3 20 07-191 F: +49 (0) 30 / 3 20 07-111 F: +49 (0) 30 / 3 20 07-107 [email protected] [email protected] www.escpeurope.eu ESCP Europe, Working Paper No. 69 – 08/19 ABSTRACT: E-commerce has grown considerably in recent decades and has had a disruptive impact on the retail industry. In this context, Amazon, one of the major players in (online) retailing and beyond, has been able to expand its business activities continuously in many countries. The present case study sheds light on the internationalization of Amazon, with a particular focus on the company’s acquisitions. The study illustrates that Amazon’s acquisitions over the last decades had two major objectives. First, acquisitions helped Amazon enter new markets and strengthen its presence in specific regions. -

Company Analysis: Team C2X
Company Analysis: Team C2X History The company was founded in 1994, spurred by what Bezos called his "regret minimization framework", which he described as his effort to fend off regret for not staking a claim in the Internet gold rush. The company began as an offline bookstore. While the largest brick-and-mortar bookstores and mail-order catalogs might offer 200,000 titles, an online bookstore could sell far more. Bezos wanted a name for his company that began with "A" so that it would appear early in alphabetic order. He began looking through the dictionary and settled on "Amazon" because it was a place that was "exotic and different" and it was the river he considered the biggest in the world, as he hoped his company would be. Since 2000, Amazon's logotype is an arrow leading from A to Z, representing that they carry every product from A to Z. Amazon's initial business plan was unusual. The company did not expect a profit for four to five years. Its "slow" growth provoked stockholder complaints that the company was not reaching profitability fast enough. When the dot-com bubble burst, and many e-companies went out of business, Amazon persevered, and finally turned its first profit in the fourth quarter of 2001: $5 million or 1¢ per share, on revenues of more than $1 billion. The profit, although it was modest, served to demonstrate that the business model could be profitable. In 1999, Time magazine named Bezos the Person of the Year, recognizing the company's success in popularizing online shopping. -

Amazon Was Founded in 1994, Spurred by What Bezos Called
Introduction: Amazon was founded in 1994, spurred by what Bezos called "regret minimization framework", his effort to fend off regret for not staking a claim in the Internet gold rush "In his typically analytic way, Bezos cast his decision in what he calls the "regret- minimization framework." He imagined that he was 80 years old and looking back at his life. And suddenly everything became clear to him. When he was 80, he'd never regret having missed out on a six-figure Christmas bonus; he wouldn't even regret having tried to build an online business and failed. "In fact, I'd have been proud of that, proud of myself for having taken that risk and tried to participate in that thing called the Internet that I thought was going to be such a big deal. It was like the wild, wild West, a new frontier. And I knew that if I didn't try this, I would regret it. And that would be inescapable." The company began as an online bookstore named "Cadabra.com", a name quickly abandoned for sounding like "cadaver"; while the largest brick-and-mortar bookstores and mail-order catalogs for books might offer 200,000 titles, an on-line bookstore could offer more. Bezos renamed the company "Amazon" after the world's biggest river. Since 2000, Amazon's logotype is an arrow leading from A to Z, representing the desire to sell many products. The domain amazon.com attracted at least 615 million visitors annually by 2008 according to a Compete.com survey. This was twice the numbers of walmart.com. -

ONLINE MUSIC DISTRIBUTION the Faculty of The
ONLINE MUSIC DISTRIBUTION A THESIS Presented to The Faculty of the Department of Economics and Business The Colorado College In Partial Fulfillment of the Requirements for the Degree Bachelor of Arts By Jeffrey A. Moore May 2010 ONLINE MUSIC DISTRIBUTION Jeffrey Moore May, 2010 Economics Abstract The music industry has seen many new forms of technology that have helped shape it to become the multi-billon dollar industry it has become today. The Internet is currently changing how artists are distributing their music as well as how consumers are receiving it. The ease of which an artist can distribute their music across the country without the help of a record label has lead to a new question as to whether or not a record contract is still necessary for an artist to succeed in the industry. This study will look at groups from the Front Range of Colorado at different stages in their musical careers to see exactly how they are using the Internet to distribute their music and to find out if any have achieved any level of financial success doing so. KEYWORDS: Music Industry, Internet Distribution ON MY HONOR, I HAVE NEITHER GIVEN NOR RECEIVED UNAUTHORIZED AID ON THIS THESIS Signature TABLE OF CONTENTS ABSTRACT iii ACKNOWLEDGEMENTS iv 1 INTRODUCTION 1 2 LITERATURE REVIEW 6 2.1 Overview of the Music Industry 6 2.2 Pricing Strategies and Internet Distribution 8 2.3 The Music Industry Market Structure and Value Chain 10 2.4 Piracy and the Music Industry 14 3 RELEVANT THEORY 17 3.1 State of the Industry Pre-Internet 18 3.2 The Introduction of the -
Social Networks, Virtual Worlds, and the Shadow Internet : the Explosion of Virtual Identity and the Anonymous Economy
Social Networks, Virtual Worlds, and the Shadow Internet : The Explosion of Virtual Identity and the Anonymous Economy Scott Dueweke 0 The Comprehensive National Cybersecurity Initiative (CNCI) Goals: To establish a front line of defense against today’s immediate threats by creating or enhancing shared situational awareness of network vulnerabilities, threats, and events within the Federal Government—and ultimately with state, local, and tribal governments and private sector partners—and the ability to act qu ickly to red uce o ur c urrent vu lnerabilities and prev ent intru sions. To defend against the full spectrum of threats by enhancing U.S. counterintelligence capabilities and increasing the security of the supply chain for keyyg information technologies. To strengthen the future cybersecurity environment by expanding cyber education; coordinating and redirecting research and development efforts across the Federal Government; and working to define and develop strategies to deter hostile or malicious activity in cyberspace. 1 CyberCyber--environmentsenvironments are changing rapidly Yesterday Today yy chnolog ee T Mainframe PCs Computers Web 1.0 Web 2.0 Mobile Government scientists Bu siness u sers of Pre-teens all industries Trained technicians Seniors Educators and Machine language Non-expert users administration People developers Casual users Researchers Expert Users Business, Education, The World Research Users Spectators Participants 2 These environments depend on Virtual Identities Social Networks Virtual Worlds Games -
(50), Estadounidense, Fundador Y CEO De Amazon.Com
LIDERAZGO JEFF (50), ESTADOUNIDENSE, FUNDADOR Y CEO DE AMAZON.COM para evacuar a la población, en caso de ser necesario”. Atento Todavía hoy lee todos los correos que envían los usuarios, hábito que comenzó cuando Amazon estaba en BEZOS “etapa garaje”. undador del imperio minorista online Amazon.com, y flamante dueño del periódico The Washington Post, Jeff Bezos sigue ex- Obsesivo pandiendo sus fronteras. Tras haber absorbido a 35 empresas de En las reuniones de Amazon.com, Be- Internet en los últimos ocho años, y más de 40 en los últimos 10, zos siempre deja una silla vacía que Fahora quiere llevar su visión al espacio exterior. representa al cliente, a quien él llama “el último jefe”. LO QUE HA HECHO portátil Kindle, y la tablet Kindle Fire Original Después de graduarse en Ciencias de en 2011. Y mientras muchas “dotcoms” A diferencia del común de las com- la Computación e Ingeniería Eléctrica sucumbieron con la explosión de la pañías de Silicon Valley, en Amazon. en la Universidad de Princeton, Bezos burbuja bursátil a finales de los ’90, com no hay dispensers de snacks, ni trabajó en varias firmas de Wall Street, Amazon prosperó con ventas anuales decoración estrafalaria, ni salarios exa- incluidas Fitel, Bankers Trust y D. E. que saltaron de US$ 510.000 en 1995, a gerados. Bezos prefiere premiar a los Shaw. También pasó por las filas de US$ 67.900 millones en 2014. empleados con acciones, “para que McKinsey, donde en 1990 fue nom- Fascinado desde niño con los viajes piensen y actúen como dueños”. brado el vicepresidente más joven de al espacio, Bezos creó Blue Origin en la consultora. -

Merger Policy in Digital Markets: an Ex-Post Assessment
1836 Discussion Papers Deutsches Institut für Wirtschaftsforschung 2019 Merger Policy in Digital Markets: An Ex-Post Assessment Elena Argentesi, Paolo Buccirossi, Emilio Calvano, Tomaso Duso, Alessia Marrazzo and Salvatore Nava Opinions expressed in this paper are those of the author(s) and do not necessarily reflect views of the institute. IMPRESSUM © DIW Berlin, 2019 DIW Berlin German Institute for Economic Research Mohrenstr. 58 10117 Berlin Tel. +49 (30) 897 89-0 Fax +49 (30) 897 89-200 http://www.diw.de ISSN electronic edition 1619-4535 Papers can be downloaded free of charge from the DIW Berlin website: http://www.diw.de/discussionpapers Discussion Papers of DIW Berlin are indexed in RePEc and SSRN: http://ideas.repec.org/s/diw/diwwpp.html http://www.ssrn.com/link/DIW-Berlin-German-Inst-Econ-Res.html Merger Policy in Digital Markets: An Ex-Post Assessment* Elena Argentesi, University of Bologna Paolo Buccirossi, Lear Emilio Calvano, University of Bologna and Toulouse School of Economics Tomaso Duso,+ Deutsches Institut für Wirtschaftsforschung (DIW Berlin), TU Berlin, CEPR, and CESifo Alessia Marrazzo Lear and University of Bologna Salvatore Nava Lear Abstract: This paper presents a broad retrospective evaluation of mergers and merger decisions in the digital sector. We first discuss the most crucial features of digital markets such as network effects, multi-sidedness, big data, and rapid innovation that create important challenges for competition policy. We show that these features have been key determinants of the theories of harm in major merger cases in the past few years. We then analyse the characteristics of almost 300 acquisitions carried out by three major digital companies –Amazon, Facebook, and Google – between 2008 and 2018. -

The Top 10 Alternative Sources for Goodreads
Supplemental Content to the article “Goodreads: Social Media Meets Readers Advisory,” appearing in the July/August 2013 issue of Online Searcher (Vol. 37, No. 4), pp. 38–41. SEARCHER’S VOICE The Top 10 Alternative Sources for Goodreads any libraries are now using existing social media systems for book recommendations as a way to Mengage with their users and move into the new work of social book recommendation. A quick poll of information professionals, who have decided to look beyond Goodreads for some good reads, brings up some interesting options. Here are the top suggestions from the pros. Bookish BookLikes and find other interesting blogs, bookish.com/home booklikes.com writers and avid readers.” This is a new, widely hyped project of It has the same look and feel as three well-known publishers, hoping Goodreads and allows for similar i09 Book Club to more directly connect authors and functions in organizing, sharing, io9.com/tag/io9-book-club readers through their publishers. and rating books with a strong social “io9 is a daily publication that “Bookish taps the expertise of authors, sensibility. “BookLikes gathers book covers science, science fiction, their editors and their publishers to lovers, book bloggers, reviews, writers and the future.” Its book club find you the best reads. Tell us which and avid readers from all over the operates as an online book books you like and we’ll show you world who can share their reviews discussion that often includes more like them.” and other writings, reading updates the book’s author as well. > JUL | AUG 2013 ONLINE SEARCHER SUPPLEMENTAL CONTENT SC1 IndieBRAG ratings and other social aspects.