Wind Tunnel Application of a Pressure-Sensitive Paint Technique to a Double Delta Wing Model at Subsonic and Transonic Speeds
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

TOC for GSA Pricing
Brunswick Commercial & Government Products 2005 Price List for Indiana Department of Natural Resources Contract #RSP-5-52 Brunswick Commercial & Government Products, Inc. reserves the right to modify or discontinue models, equipment or prices at any time without incurring obligation. BUILT FOR THE MISSION.TM BRUNSWICK COMMERCIAL & GOVERNMENT PRODUCTS, INC. 420 Megan Z Avenue • Edgewater, FL 32132 • Phone 386.423.2900 • Fax 386.423.9187 www.brunswickCGboats.com ENGINE PRE-RIG KITS INCLUDE THE FOLLOWING: MERCURY SINGLE O/B ENGINE PRE-RIG (61420) MERCURY DUAL O/B ENGINE PRE-RIG (61421) FUEL FILTER/WATER SEPERATOR (BOATS WITH BUILT IN FUEL TANK) (SEE NOTE 1) (2) FUEL FILTER/WATER SEPERATOR (BOATS WITH BUILT IN FUEL TANK) (SEE NOTE 1) ELECTRIC FUEL GAUGE (BOATS WITH BUILT IN FUEL TANK) ELECTRIC FUEL GAUGE (BOATS WITH BUILT IN FUEL TANK) BINNACLE BINNACLE WIRING HARNESS, KEY SWITCH & ALARM HORN WIRING HARNESS, KEY SWITCH & ALARM HORN SHIFT & THROTTLE CABLES SHIFT & THROTTLE CABLES TACHOMETER (2) TACHOMETER VOLTMETER (2) VOLTMETER TRIM GAUGE (2) TRIM GAUGE HOUR METER (2) HOUR METER ENGINE TIE BAR KIT BOMBARDIER SINGLE O/B ENGINE PRE-RIG (61422) BOMBARDIER DUAL O/B ENGINE PRE-RIG (61423) FUEL FILTER/WATER SEPERATOR (BOATS WITH BUILT IN FUEL TANK) (2) FUEL FILTER/WATER SEPERATOR (BOATS WITH BUILT IN FUEL TANK) ELECTRIC FUEL GAUGE (BOATS WITH BUILT IN FUEL TANK) ELECTRIC FUEL GAUGE (BOATS WITH BUILT IN FUEL TANK) BINNACLE BINNACLE WIRING HARNESS, KEY SWITCH & ALARM HORN WIRING HARNESS, KEY SWITCH & ALARM HORN SHIFT & THROTTLE CABLES SHIFT & THROTTLE -

The Elements of Wood Ship Construction
THE ELEMENTS OF WOOD SHIP CONSTRUCTION Digitized by the Internet Archive in 2007 with funding from Microsoft Corporation http://www.archive.org/details/elementsofwoodshOOcurtrich Digitized file changed into text by AK, Feb. 2012 THE ELEMENTS OF WOOD SHIP CONSTRUCTION THE ELEMENTS OF WOOD SHIP CONSTRUCTION BY W. H. CURTIS NAVAL ARCHITECT AND MARINE ENGINEER FIRST EDITION McGRAW-HILL BOOK COMPANY, INC. 239 WEST 39TH STREET. NEW YORK ----------- LONDON: HILL PUBLISHING CO., Ltd. 6 & 8 BOUVERIE ST., E. C 1919 COPYRIGHT. 1919, BY THE MCGRAW-HILL BOOK COMPANY, INC. ------------ COPYRIGHT, 1918, BY W. H. CURTIS. THE MAPLE PRESS YORK PA GENERAL PREFACE ------------- Preface to Pamphlet, Part I, issued by the United States Shipping Board Emergency Fleet Corporation, for use in its classes in Wood Shipbuilding. This text on wood shipbuilding was prepared by W. H. Curtis, Portland, Oregon, for the Education and Training Section of the Emergency Fleet Corporation. It is intended for the use of carpenters and others, who, though skilled in their work, lack the detail knowledge of ships necessary for the efficient performance of their work in the yard. Sea-going vessels are generally built according to the rules of some Classification Society, and all important construction and fastening details have to be passed upon by the Classification Society under whose inspection the vessel is to be built. Due to this fact, requirements may vary in detail from types of construction here explained. It is hoped, however, that this book may be helpful to shipbuilding classes and to individual men in the yard. EDUCATION AND TRAINING SECTION UNITED STATES SHIPPING BOARD EMERGENCY FLEET CORPORATION In presenting this work due credit is given Mr. -

ACHILLES INFLATABLE BOATS a Division of Achilles USA, Inc
2018 INFLATABLE BOATS It begins with the best fabric. Designed and built with safety Because our boats last, Our quality CSM fabric has and performance in mind. so does our support. such a great reputation in the From built-in safety features like We provide our dealers and inflatable boat industry that the strongest four-layer seam customers with comprehensive other inflatable boat manufac- construction in the industry to and responsive post-sales turers buy their fabric from us. custom designs engineered to support in every aspect of It all starts with an exterior complement and enhance the Achilles ownership. Our The Achilles boating experience begins with best inflatable coating of our custom CSM performance of each of our customer and mobile-friendly boat fabric, designs and options and ends with unsurpassed over a heavy duty fabric which boats, boaters get more out of web site not only offers customer support for as long as you own your boat. makes our inflatables virtually an Achilles. Our boats are built comprehensive information In between you will enjoy years of on-the-water activities impervious to the elements, oil, to not only last, but to also about our current models, in the most durable inflatable boat you can find. gasoline and abrasions. And it deliver the practicality you but also on all Achilles boats ends with two interior coatings expect from an inflatable with- produced since 1978. of Chloroprene for unsurpassed out sacrificing the performance CSM exterior for air retention. you want from any boat. toughness www.achillesboats.com Heavy-duty Nylon or Polyester core fabric A SMOOTH, SIMPLE OAR SYSTEM NON-CORROSIVE CHECK VALVES Two layers of Chloroprene We invented the fold-down, locking oar system All Achilles valves are non-corrosive with no moving for unsurpassed that makes rowing a breeze while keeping oars parts that might break. -

Swift Trawler 44
Swift Trawler 44 General Equipment list - North America GENERAL SPECIFICATIONS___________________________ • Overall Length (L.O.A)*: 13,88 m 45’6’’ • Hull length: 12,17 m 39’11’’ • Overall width: 4,25 m 13’11’’ • Hull Beam: 4,25 m 13’11’’ • Light displacement (EC): 10 870 kg 23,957 lbs • Air draft**: 3,86 m 12’8’’ • Air draft***: 7,76 m 25’6’’ •Draft: 1,05m 3’5’’ • Fuel tank: 1 400 L 370 US Gal • Water tank: 640 L 169 US Gal • Holding tank: 120 L 32 US Gal • Engine power: 2 x 300 HP 2x300HP * (with aft swim platform + Anchor in position) ** (with mast folded) *** (with mast in position) ARCHITECTS / DESIGNERS ___________________________ • Naval Architect: M. JOUBERT & B. NIVELT - BENETEAU POWER • Design: P. FRUTSCHI CE CERTIFICATION __________________________________ • Category B: 12 people • Category C: 14 people July 01, 2018 - (non-binding document) Code Beneteau M100136 (Q) US Swift Trawler 44 General Equipment list - North America STANDARD EQUIPMENT FLY BRIDGE • Flybridge self-bailing CONSTRUCTION ____________________________________ • Stainless steel staircase and access ramp to flybridge with teak treads • Grey tinted windscreen in PMMA HULL • Access via PMMA hatch Composition: • Stainless steel pulpit surrounding aft of flybridge • Sandwich (polyester resin - fiberglass / balsa core) • White lacquered swing mast, Navigation light mounting, Radar, Aerial • White gel coat • Central steering console • Structural hull counter molding in monolithic laminate (polyester resin - • Control panel including: Electrical engine controls, Electric -
2008 INTERNATIONAL OPTIMIST CLASS RULES Authority*: International Sailing Federation
2008 INTERNATIONAL OPTIMIST CLASS RULES Authority*: International Sailing Federation * The ISAF is not a National Authority as described in these rules CONTENTS Page Rule 2 1 GENERAL 2 2. ADMINISTRATION 2 2.1 English language 2 2.2 Builders 3 2.3 International Class Fee 3 2.4 Registration and measurement certificate 4 2.5 Measurement 4 2.6 Measurement instructions 5 2.7 Identification marks 6 2.8 Advertising 6 3 CONSTRUCTION AND MEASUREMENT RULES 6 3.1 General 6 3.2 Hull 6 3.2.1 Materials - GRP 7 3.2.2 Hull measurement rules 10 3.2.3 Hull construction details - GRP 3.2.4 Hull construction details - Wood and Wood/Epoxy (See Appendix A, p 25) 3.2.5 Not used 12 3.2.6 Fittings 13 3.2.7 Buoyancy 14 3.2.8 Weight 14 3.3 Daggerboard 16 3.4 Rudder and Tiller 19 3.5 Spars 19 3.5.2 Mast 20 3.5.3 Boom 21 3.5.4 Sprit 21 3.5.5 Running rigging 22 4 ADDITIONAL RULES 5 (spare rule number) 23 6 SAIL 23 6.1 General 23 6.2 Mainsail 6.3 Spare rule number 6.4 Spare rule number 25 6.5 Class Insignia, National Letters, Sail Numbers and Luff Measurement Band 26 6.6 Additional sail rules 27 APPENDIX A: Rules specific to Wood and Wood/Epoxy hulls. 29 PLANS. Index of current official plans. 1 GENERAL 1.1 The object of the class is to provide racing for young people at low cost. -

International Optimist Class Rules CONTENTS
International Optimist Dinghy Association 2018 www.optiworld.org International Optimist Class Rules CONTENTS Page Rule 2 1 GENERAL 2 2. ADMINISTRATION 2 2.1 English language 2 2.2 Builders 3 2.3 World Sailing Class Fee 3 2.4 Registration and Measurement Certificate 4 2.5 Measurement 4 2.6 Measurement Instructions 5 2.7 Identification Marks 6 2.8 Advertising 6 3 CONSTRUCTIONAND MEASUREMENT RULES 6 3.1 General 6 3.2 Hull 6 3.2.1 Materials - GRP 7 3.2.2 Hull Measurement Rules 10 3.2.3 Hull Construction Details - GRP 12 3.2.4 Hull Construction Details - Wood and Wood/Epoxy (See Appendix A, p 27) 3.2.5 Not used 12 3.2.6 Fittings 13 3.2.7 Buoyancy 14 3.2.8 Weight 14 3.3 Daggerboard 16 3.4 Rudder and Tiller 19 3.5 Spars 19 3.5.2 Mast 20 3.5.3 Boom 21 3.5.4 Sprit 21 3.5.5 Running Rigging 22 4 ADDITIONAL RULES 5 (spare rule number) 23 6 SAIL 23 6.1 General 23 6.2 Sailmaker 6.3 Mainsail 6.4 Dimensions 25 6.5 Class Insignia, National Letters, Sail Numbers and Luff Measurement Band 26 6.6 Additional Rules (Sail) 27 APPENDIX A: Rules Specific to Wood and Wood/Epoxy Hulls. 29 PLANS: Index of current official plans. 30 Addendum - Information and References to World Sailing Advertising Code 1 1 GENERAL 1.1 The object of the class is to provide racing for young people at low cost. 1.2 The Optimist is a One-Design Class Dinghy. -

Boats of Currituck (Richards and Stewart, Eds., 2016) Program in Maritime Studies Report No
Boats of and Stewart, eds., 2016) Currituck (Richards University) 23 (East Carolina Program in Maritime Studies Report No. In the fall of 2013 and the summer of 2014, graduate students from East Carolina University’s Program in Maritime Students, in collaboration Boats of Currituck: with the UNC-Coastal Studies Institute, carried out a project recording six watercraft from a collection of historical small watercraft collected and An Analysis of Six Watercraft from maintained by the Whalehead Preservation Trust in Currituck County, North Carolina. the Whalehead Preservation Trust Collection This volume contains six chapters that serve as the technical reports Edited by Nathan Richards and David J. Stewart concerning these six vessels. Each chapter reports the process of recording the boats and their histories and also engages in interpretation and analysis of the form, function, and methods of construction. In some cases, examinations of modifications, repairs, and wear and tear are also made. The publication intends to communicate the results of maritime-focused historic preservation activities concerning a small part of Currituck County’s legacy of boat-building. Project Partners: ISBN 978-1-365-44608-5 90000 Program in Maritime Studies 7813659 446085 East Carolina University Greenville, North Carolina Research Report No. 23 (2016) BOATS OF CURRITUCK: AN ANALYSIS OF SIX WATERCRAFT FROM THE WHALEHEAD PRESERVATION TRUST COLLECTION Nathan Richards and David J. Stewart (editors) Chapters by: Jeremy Borrelli Ryan Bradley Kara Davis Chelsea Freeland Phillip Hartmeyer Sara Kerfoot Kelci Martinsen Allison Miller Michele Panico Adam Parker Julie Powell Alyssa Reisner William Sassorossi Emily Steedman Sonia Valencia Jeneva Wright Caitlin Zant i Research Report No. -

The Effect of Tailboom Strakes and Vertical Fin Modifications on the Performance and Handling Qualities of OH-58 Helicopters
University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Masters Theses Graduate School 5-2008 The Effect of Tailboom Strakes and Vertical Fin Modifications on the Performance and Handling Qualities of OH-58 Helicopters John A. Wade University of Tennessee - Knoxville Follow this and additional works at: https://trace.tennessee.edu/utk_gradthes Recommended Citation Wade, John A., "The Effect of Tailboom Strakes and Vertical Fin Modifications on the erP formance and Handling Qualities of OH-58 Helicopters. " Master's Thesis, University of Tennessee, 2008. https://trace.tennessee.edu/utk_gradthes/477 This Thesis is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Masters Theses by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a thesis written by John A. Wade entitled "The Effect of Tailboom Strakes and Vertical Fin Modifications on the erP formance and Handling Qualities of OH-58 Helicopters." I have examined the final electronic copy of this thesis for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Master of Science, with a major in Aviation Systems. Richard Ranaudo, Major Professor We have read this thesis and recommend its acceptance: Stephen Corda, Uwe P. Solies Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) To the Graduate Council: I am submitting herewith a thesis written by John A. -

Nautical Terms for the Model Ship Builder
Nautical Terms For The Model Ship Builder Compliments of www.modelshipbuilder.com “Preserving the Art of Model Ship Building for a new Generation” January 2007 Nautical Terms For The Model Ship Builder Copyright, 2007 by modelshipbuidler.com Edition 1.0 All rights reserved under International Copyright Conventions “The purpose of this book is to help educate.” For this purpose only may you distribute this book freely as long as it remain whole and intact. Though we have tried our best to ensure that the contents of this book are error free, it is subject to the fallings of human frailty. If you note any errors, we would appreciate it if you contact us so they may be rectified. www.modelshipbuilder.com www.modelshipbuilder.com 2 Nautical Terms For The Model Ship Builder Contents A......................................................................................................................................................................4 B ......................................................................................................................................................................5 C....................................................................................................................................................................12 D....................................................................................................................................................................20 E ....................................................................................................................................................................23 -

Unit 2 SHIPS and SHIP TERMS
Unit 2 SHIPS AND SHIP TERMS STRUCTURAL MEMBERS OF A SHIP Basic terms shell plating compartment strake stem keel frame deck beam tank top bracket floor girder stringer buoyancy stern post strength hull stability angle bar bulkhead stiffener stringer web sheer strake rudder post The forward end of the ship is called the bow, the after end is the stern, and halfway between the two is amidships. The beam of the ship is the distance between the two ship's sides. The hull or the body of the ship includes the outer skin or shell, and all the members (konstrukcijski elementi) and parts which hold this shell together, divide it into compartments and give it strength and rigidity. Three basic requirements of ships are the ability to float (buoyancy), the ability to stay together (strength), and the ability to stay right side up (stability). The shell plating (oplata) is the outer skin of the ship and is made up of a great many steel plates fastened together by welding. Each horizontal row of plating is called a strake (voj). Strakes are usually lettered A-B-C-D, etc., beginning with the row next to the keel (kobilica). This strake is called the garboard strake (dokobilični voj) while the top strake is called the sheer strake (uzvojni voj). The two essentials of the shell are watertightness and strength. The flat keel of a ship is the row at the bottom of the ship extending from the bow to the stern along the centreline. Decks, corresponding to the floors of a house, are flat sections of steel plates. -

5.5 Skuldelev 5
Kapitel 5-5.qxd 4/1/02 8:55 PM Side 1 5.5 Skuldelev 5 5.5.1 Excavation • 246 5.5.3 Reconstruction of the ship in torso • 264 Position in the barrier • 246 Models • 264 State of preservation • 246 Lines and torso-drawing • 266 Excavation, raising and documentation • 247 Type and size of the ship • 266 5.5.2 Description of the preserved parts 5.5.4 Analysis of the ship from construction of the ship • 250 to scuttling • 269 The keel • 250 Reused parts and repairs • 269 Stems • 251 The construction phase • 273 Planking • 251 The stem • 273 Framing system • 255 Planking • 273 The floor timbers • 255 Internal timbers • 273 Bitis, beams, knees and stringers • 257 Design principles • 273 Other parts of the framing system • 259 Wear and other traces from the active use Hull parts related to propulsion, of the ship • 274 steering and equipment • 261 The scuttling and subsequent disintegration • 274 The rudder • 261 5 5 5 274 The keelson • 261 . Dating • Rigging details • 262 5 5 6 276 Oarports and shield-rack • 262 . General conclusion and parallels • Summary of the Skuldelev 5 evidence • 276 Parallels in other Scandinavian finds • 277 245 Kapitel 5-5.qxd 4/1/02 9:01 PM Side 2 5.5.1 Excavation could probably not be moved and consequently had to be left on the spot where it had run aground. The fact that the Position in the barrier drain-plug was not found in position aft in the garboard The wreck Skuldelev 5 was situated along the northern edge strake indicates that the ship had eventually been aban- of the Peberrenden channel, oriented with the bow pointing doned here deliberately. -
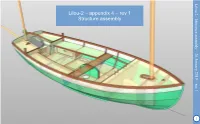
EN-Lilou2-Append4-As
Lilou 2 - Structure assembly – 26 January 2019 – rev 1 1 1 rev Structureassembly Lilou-2appendix – 4– Lilou 2 - Structure assembly – 26 January 2019 – rev 1 2 : Bulkheads are not bevelled Important edges in upper parts Glue the trims protecting the plywood Bulkheads preparation: Lilou 2 - Structure assembly – 26 January 2019 – rev 1 3 Bulkheads preparation: for the fore locker shutter. Glue the batten/cleat 22 x 22 as shown. Glue the rabbet on the mast bulkhead (fore face) Lilou 2 - Structure assembly – 26 January 2019 – rev 1 4 Glue the batten/cleat 22 x 22 as shown. Fore Fore bulkhead, aft face: Lilou 2 - Structure assembly – 26 January 2019 – rev 1 5 Aft bulkhead, fore face: Glue the batten/cleat 22 x 22 as shown. Lilou 2 - Structure assembly – 26 January 2019 – rev 1 6 Note the motor support and the doubler glued inside the buoyancybut the The compartment.doubler is glued now, support will be screwed later according to the actual motor. Buy them in advance to make the cut-out before assembling of these parts (it will be more difficult to cut at a later stage). and sides of the motor well) are fitted with dinghy type watertight hatch covers. Overall diameter is maximum 250 mm. The The bulkheads of the buoyancy compartment (fore bulkhead Lilou 2 - Structure assembly – 26 January 2019 – rev 1 7 before the panel is glued down. Maximum Maximum overall diameter is 220 mm. ballast and the bilge pump suction space. Cut-out may be done at a later stage, just Dinghy hatch covers give access to the water Lilou 2 - Structure assembly – 26 January 2019 – rev 1 8 assembly ties.