Learning to Play Like the Great Pianists
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Season 2014-2015
27 Season 2014-2015 Thursday, May 7, at 8:00 Friday, May 8, at 2:00 The Philadelphia Orchestra Saturday, May 9, at 8:00 Cristian Măcelaru Conductor Sarah Chang Violin Ligeti Romanian Concerto I. Andantino— II. Allegro vivace— III. Adagio ma non troppo— IV. Molto vivace First Philadelphia Orchestra performances Beethoven Symphony No. 1 in C major, Op. 21 I. Adagio molto—Allegro con brio II. Andante cantabile con moto III. Menuetto (Allegro molto e vivace)—Trio— Menuetto da capo IV. Adagio—Allegro molto e vivace Intermission Dvořák Violin Concerto in A minor, Op. 53 I. Allegro ma non troppo—Quasi moderato— II. Adagio ma non troppo—Più mosso—Un poco tranquillo, quasi tempo I III. Finale: Allegro giocoso ma non troppo Enescu Romanian Rhapsody in A major, Op. 11, No. 1 This program runs approximately 1 hour, 50 minutes. The May 7 concert is sponsored by MedComp. The May 8 and 9 concerts are sponsored by the Blanche and Irving Laurie Foundation. designates a work that is part of the 40/40 Project, which features pieces not performed on subscription concerts in at least 40 years. Philadelphia Orchestra concerts are broadcast on WRTI 90.1 FM on Sunday afternoons at 1 PM. Visit www.wrti.org to listen live or for more details. 228 Story Title The Philadelphia Orchestra Jessica Griffin The Philadelphia Orchestra is one of the preeminent orchestras in the world, renowned for its distinctive sound, desired for its keen ability to capture the hearts and imaginations of audiences, and admired for a legacy of imagination and innovation on and off the concert stage. -

October 2015
October 2015 Bertrand Chamayou INSIDE: Ian Bostridge | Sarah Connolly Ehnes Quartet | Thomas Hampson Alina Ibragimova & Cédric Tiberghien Magdalena Kozˇená & Mitsuko Uchida Steven Isserlis | Robert Levin Sandrine Piau | Christoph Prégardien Stile Antico | Vox Luminis And many more Box Office 020 7935 2141 Online Booking www.wigmore-hall.org.uk How to Book Wigmore Hall Box Office 36 Wigmore Street, London W1U 2BP In Person 7 days a week: 10 am – 8.30 pm. Days without an evening concert 10 am – 5 pm. No advance booking in the half hour prior to a concert. Please note that the Box Office with be closed for bookings in person from Monday 27 July to Friday 4 September. By Telephone: 020 7935 2141 7 days a week: 10 am – 7 pm. Days without an evening concert 10 am – 5 pm. There is a non-refundable £3.00 administration fee for each transaction, which includes the return of your tickets by post if time permits. Online: www.wigmore-hall.org.uk 7 days a week; 24 hours a day. There is a non-refundable £2.00 administration charge. Standby Tickets Standby tickets for students, senior citizens and the unemployed are available from one hour before the performance (subject to availability) with best available seats sold at the lowest price. NB standby tickets are not available for Lunchtime and Coffee Concerts. Group Discounts Discounts of 10% are available for groups of 12 or more, subject to availability. Latecomers Latecomers will only be admitted during a suitable pause in the performance. Facilities for Disabled People full details available from 020 7935 2141 or [email protected] Wigmore Hall has been awarded the Bronze Charter Mark from Attitude is Everything TICKETS Unless otherwise stated, tickets are A–D divided into five prices ranges: BALCONY Stalls C – M W–Y Highest price T–V Stalls A – B, N – P Q–S 2nd highest price Balcony A – D N–P 2nd highest price STALLS Stalls BB, CC, Q – S C–M 3rd highest price A–B Stalls AA, T – V CC CC 4th highest price BB BB PLATFORM Stalls W – Y AAAA AAAA Lowest price This brochure is available in alternative formats. -

Cds by Composer/Performer
CPCC MUSIC LIBRARY COMPACT DISCS Updated May 2007 Abercrombie, John (Furs on Ice and 9 other selections) guitar, bass, & synthesizer 1033 Academy for Ancient Music Berlin Works of Telemann, Blavet Geminiani 1226 Adams, John Short Ride, Chairman Dances, Harmonium (Andriessen) 876, 876A Adventures of Baron Munchausen (music composed and conducted by Michael Kamen) 1244 Adderley, Cannonball Somethin’ Else (Autumn Leaves; Love For Sale; Somethin’ Else; One for Daddy-O; Dancing in the Dark; Alison’s Uncle 1538 Aebersold, Jamey: Favorite Standards (vol 22) 1279 pt. 1 Aebersold, Jamey: Favorite Standards (vol 22) 1279 pt. 2 Aebersold, Jamey: Gettin’ It Together (vol 21) 1272 pt. 1 Aebersold, Jamey: Gettin’ It Together (vol 21) 1272 pt. 2 Aebersold, Jamey: Jazz Improvisation (vol 1) 1270 Aebersold, Jamey: Major and Minor (vol 24) 1281 pt. 1 Aebersold, Jamey: Major and Minor (vol 24) 1281 pt. 2 Aebersold, Jamey: One Dozen Standards (vol 23) 1280 pt. 1 Aebersold, Jamey: One Dozen Standards (vol 23) 1280 pt. 2 Aebersold, Jamey: The II-V7-1 Progression (vol 3) 1271 Aerosmith Get a Grip 1402 Airs d’Operettes Misc. arias (Barbara Hendricks; Philharmonia Orch./Foster) 928 Airwaves: Heritage of America Band, U.S. Air Force/Captain Larry H. Lang, cond. 1698 Albeniz, Echoes of Spain: Suite Espanola, Op.47 and misc. pieces (John Williams, guitar) 962 Albinoni, Tomaso (also Pachelbel, Vivaldi, Bach, Purcell) 1212 Albinoni, Tomaso Adagio in G Minor (also Pachelbel: Canon; Zipoli: Elevazione for Cello, Oboe; Gluck: Dance of the Furies, Dance of the Blessed Spirits, Interlude; Boyce: Symphony No. 4 in F Major; Purcell: The Indian Queen- Trumpet Overture)(Consort of London; R,Clark) 1569 Albinoni, Tomaso Concerto Pour 2 Trompettes in C; Concerto in C (Lionel Andre, trumpet) (also works by Tartini; Vivaldi; Maurice André, trumpet) 1520 Alderete, Ignacio: Harpe indienne et orgue 1019 Aloft: Heritage of America Band (United States Air Force/Captain Larry H. -
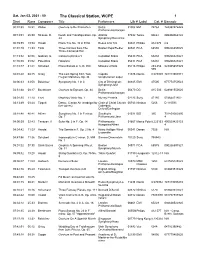
Sat, Jan 02, 2021 - 00 the Classical Station, WCPE 1 Start Runs Composer Title Performerslib # Label Cat
Sat, Jan 02, 2021 - 00 The Classical Station, WCPE 1 Start Runs Composer Title PerformersLIb # Label Cat. # Barcode 00:01:30 10:31 Weber Overture to Der Freischutz Berlin 01006 EMI 74764 724357476423 Philharmonic/Karajan 00:13:0125:39 Strauss, R. Death and Transfiguration, Op. Atlanta 07032 Telarc 80661 089408066122 24 Symphony/Runnicles 00:39:55 19:54 Haydn Piano Trio No. 36 in E flat Beaux Arts Trio 04027 Philips 432 070 n/a 01:01:1911:33 Falla Three Dances from The Boston Pops/Fiedler 04581 RCA 68550 090266855025 Three-Cornered Hat 01:13:5202:08 Gabrieli, G. Canzona prima a 5 Canadian Brass 05433 RCA 63238 090266323821 01:16:00 01:02 Palestrina Hosanna Canadian Brass 05433 RCA 63238 090266323821 01:18:1741:41 Schubert Piano Sonata in A, D. 959 Mitsuko Uchida 05116 Philips 289 456 028945657929 579 02:01:2804:15 Grieg The Last Spring from Two Capella 11036 Naxos 8.578009 747313800971 Elegiac Melodies, Op. 34 Istropolitana/Leaper 02:06:4343:50 Balakirev Symphony No. 1 in C City of Birmingham 00845 EMI 47505 077774750523 Symphony/Jarvi 02:51:4808:17 Beethoven Overture to Egmont, Op. 84 Berlin 00470 DG 415 506 028941550620 Philharmonic/Karajan 03:01:3511:14 Liszt Mephisto Waltz No. 1 Murray Perahia 02233 Sony 47180 07464471802 03:13:4903:44 Tippett Dance, Clarion Air (madrigal for Choir of Christ Church 00783 Nimbus 5266 D 110593 five voices) Cathedral, Oxford/Darlington 03:18:4840:41 Alfven Symphony No. 1 In F minor, Stockholm 01531 BIS 395 731859000395 Op. 7 Philharmonic/Jarvi 4 04:00:5932:43 Taneyev, A. -
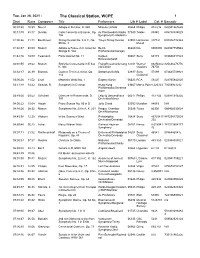
The Classical Station, WCPE 1 Start Runs Composer Title Performerslib # Label Cat
Tue, Jan 26, 2021 - The Classical Station, WCPE 1 Start Runs Composer Title PerformersLIb # Label Cat. # Barcode 00:01:30 10:39 Mozart Adagio in B minor, K. 540 Mitsuko Uchida 00264 Philips 412 616 028941261625 00:13:3945:17 Dvorak Cello Concerto in B minor, Op. du Pre/Swedish Radio 07040 Teldec 85340 685738534029 104 Symphony/Celibidache 01:00:2631:11 Beethoven String Quartet No. 9 in C, Op. Tokyo String Quartet 04508 Harmonia 807424 093046742362 59 No. 3 Mundi 01:32:3708:09 Mozart Adagio & Fugue in C minor for Berlin 06660 DG 0005830 028947759546 Strings K. 546 Philharmonic/Karajan 01:42:1618:09 Telemann Paris Quartet No. 11 Kuijken 04867 Sony 63115 074646311523 Bros/Leonhardt 02:01:5529:22 Mozart Sinfonia Concertante in E flat, Frang/Rysanov/Arcang 12341 Warner 08256462 825646276776 K. 364 elo/Cohen Classics 76776 02:32:1726:39 Brahms Clarinet Trio in A minor, Op. Stoltzman/Ax/Ma 02937 Sony 57499 074645749921 114 Classical 03:00:2611:52 Liszt Mephisto Waltz No. 1 Evgeny Kissin 06623 RCA 58420 828765842020 03:13:1834:42 Strauss, R. Symphony in D minor Hong Kong 03667 Marco Polo 8.220323 73009923232 Philharmonic/Scherme rhorn 03:49:0009:52 Schubert Overture to Rosamunde, D. Leipzig Gewandhaus 00217 Philips 412 432 028941243225 797 Orchestra/Masur 04:00:2215:04 Haydn Piano Sonata No. 50 in D Julia Cload 02053 Meridian 84083 N/A 04:16:2628:32 Mozart Symphony No. 29 in A, K. 201 Prague Chamber 05596 Telarc 80300 089408030024 Orch/Mackerras 04:45:58 12:20 Webern In the Summer Wind Philadelphia 10424 Sony 88725417 887254172024 Orchestra/Ormandy 202 04:59:4806:23 Lehar Merry Widow Waltz Richard Hayman 08261 Naxos 8.578041- 747313804177 Symphony 42 05:07:11 21:52 Rachmaninoff Rhapsody on a Theme of Entremont/Philadelphia 04207 Sony 46541 07464465412 Paganini, Op. -

Verdi Week on Operavore Program Details
Verdi Week on Operavore Program Details Listen at WQXR.ORG/OPERAVORE Monday, October, 7, 2013 Rigoletto Duke - Luciano Pavarotti, tenor Rigoletto - Leo Nucci, baritone Gilda - June Anderson, soprano Sparafucile - Nicolai Ghiaurov, bass Maddalena – Shirley Verrett, mezzo Giovanna – Vitalba Mosca, mezzo Count of Ceprano – Natale de Carolis, baritone Count of Ceprano – Carlo de Bortoli, bass The Contessa – Anna Caterina Antonacci, mezzo Marullo – Roberto Scaltriti, baritone Borsa – Piero de Palma, tenor Usher - Orazio Mori, bass Page of the duchess – Marilena Laurenza, mezzo Bologna Community Theater Orchestra Bologna Community Theater Chorus Riccardo Chailly, conductor London 425846 Nabucco Nabucco – Tito Gobbi, baritone Ismaele – Bruno Prevedi, tenor Zaccaria – Carlo Cava, bass Abigaille – Elena Souliotis, soprano Fenena – Dora Carral, mezzo Gran Sacerdote – Giovanni Foiani, baritone Abdallo – Walter Krautler, tenor Anna – Anna d’Auria, soprano Vienna Philharmonic Orchestra Vienna State Opera Chorus Lamberto Gardelli, conductor London 001615302 Aida Aida – Leontyne Price, soprano Amneris – Grace Bumbry, mezzo Radames – Placido Domingo, tenor Amonasro – Sherrill Milnes, baritone Ramfis – Ruggero Raimondi, bass-baritone The King of Egypt – Hans Sotin, bass Messenger – Bruce Brewer, tenor High Priestess – Joyce Mathis, soprano London Symphony Orchestra The John Alldis Choir Erich Leinsdorf, conductor RCA Victor Red Seal 39498 Simon Boccanegra Simon Boccanegra – Piero Cappuccilli, baritone Jacopo Fiesco - Paul Plishka, bass Paolo Albiani – Carlos Chausson, bass-baritone Pietro – Alfonso Echevarria, bass Amelia – Anna Tomowa-Sintow, soprano Gabriele Adorno – Jaume Aragall, tenor The Maid – Maria Angels Sarroca, soprano Captain of the Crossbowmen – Antonio Comas Symphony Orchestra of the Gran Teatre del Liceu, Barcelona Chorus of the Gran Teatre del Liceu, Barcelona Uwe Mund, conductor Recorded live on May 31, 1990 Falstaff Sir John Falstaff – Bryn Terfel, baritone Pistola – Anatoli Kotscherga, bass Bardolfo – Anthony Mee, tenor Dr. -

Conducting from the Piano: a Tradition Worth Reviving? a Study in Performance
CONDUCTING FROM THE PIANO: A TRADITION WORTH REVIVING? A STUDY IN PERFORMANCE PRACTICE: MOZART’S PIANO CONCERTO IN C MINOR, K. 491 Eldred Colonel Marshall IV, B.A., M.M., M.M, M.M. Dissertation Prepared for the Degree of DOCTOR OF MUSICAL ARTS UNIVERSITY OF NORTH TEXAS May 2018 APPROVED: Pamela Mia Paul, Major Professor David Itkin, Committee Member Jesse Eschbach, Committee Member Steven Harlos, Chair of the Division of Keyboard Studies Benjamin Brand, Director of Graduate Studies in the College of Music John W. Richmond, Dean of the College of Music Victor Prybutok, Dean of the Toulouse Graduate School Marshall IV, Eldred Colonel. Conducting from the Piano: A Tradition Worth Reviving? A Study in Performance Practice: Mozart’s Piano Concerto in C minor, K. 491. Doctor of Musical Arts (Performance), May 2018, 74 pp., bibliography, 43 titles. Is conducting from the piano "real conducting?" Does one need formal orchestral conducting training in order to conduct classical-era piano concertos from the piano? Do Mozart piano concertos need a conductor? These are all questions this paper attempts to answer. Copyright 2018 by Eldred Colonel Marshall IV ii TABLE OF CONTENTS Page CHAPTER 1. INTRODUCTION: A BRIEF HISTORY OF CONDUCTING FROM THE KEYBOARD ............ 1 CHAPTER 2. WHAT IS “REAL CONDUCTING?” ................................................................................. 6 CHAPTER 3. ARE CONDUCTORS NECESSARY IN MOZART PIANO CONCERTOS? ........................... 13 Piano Concerto No. 9 in E-flat major, K. 271 “Jeunehomme” (1777) ............................... 13 Piano Concerto No. 13 in C major, K. 415 (1782) ............................................................. 23 Piano Concerto No. 20 in D minor, K. 466 (1785) ............................................................. 25 Piano Concerto No. 24 in C minor, K. -

A Culture of Recording: Christopher Raeburn and the Decca Record Company
A Culture of Recording: Christopher Raeburn and the Decca Record Company Sally Elizabeth Drew A thesis submitted in partial fulfilment of the requirements for the degree of Doctor of Philosophy The University of Sheffield Faculty of Arts and Humanities Department of Music This work was supported by the Arts & Humanities Research Council September 2018 1 2 Abstract This thesis examines the working culture of the Decca Record Company, and how group interaction and individual agency have made an impact on the production of music recordings. Founded in London in 1929, Decca built a global reputation as a pioneer of sound recording with access to the world’s leading musicians. With its roots in manufacturing and experimental wartime engineering, the company developed a peerless classical music catalogue that showcased technological innovation alongside artistic accomplishment. This investigation focuses specifically on the contribution of the recording producer at Decca in creating this legacy, as can be illustrated by the career of Christopher Raeburn, the company’s most prolific producer and specialist in opera and vocal repertoire. It is the first study to examine Raeburn’s archive, and is supported with unpublished memoirs, private papers and recorded interviews with colleagues, collaborators and artists. Using these sources, the thesis considers the history and functions of the staff producer within Decca’s wider operational structure in parallel with the personal aspirations of the individual in exerting control, choice and authority on the process and product of recording. Having been recruited to Decca by John Culshaw in 1957, Raeburn’s fifty-year career spanned seminal moments of the company’s artistic and commercial lifecycle: from assisting in exploiting the dramatic potential of stereo technology in Culshaw’s Ring during the 1960s to his serving as audio producer for the 1990 The Three Tenors Concert international phenomenon. -
Brentano String Quartet
“Passionate, uninhibited, and spellbinding” —London Independent Brentano String Quartet Saturday, October 17, 2015 Riverside Recital Hall Hancher University of Iowa A collaboration with the University of Iowa String Quartet Residency Program with further support from the Ida Cordelia Beam Distinguished Visiting Professor Program. THE PROGRAM BRENTANO STRING QUARTET Mark Steinberg violin Serena Canin violin Misha Amory viola Nina Lee cello Selections from The Art of the Fugue Johann Sebastian Bach Quartet No. 3, Op. 94 Benjamin Britten Duets: With moderate movement Ostinato: Very fast Solo: Very calm Burlesque: Fast - con fuoco Recitative and Passacaglia (La Serenissima): Slow Intermission Quartet in B-flat Major, Op. 67 Johannes Brahms Vivace Andante Agitato (Allegretto non troppo) Poco Allegretto con variazioni The Brentano String Quartet appears by arrangement with David Rowe Artists www.davidroweartists.com. The Brentano String Quartet record for AEON (distributed by Allegro Media Group). www.brentanoquartet.com 2 THE ARTISTS Since its inception in 1992, the Brentano String Quartet has appeared throughout the world to popular and critical acclaim. “Passionate, uninhibited and spellbinding,” raves the London Independent; the New York Times extols its “luxuriously warm sound [and] yearning lyricism.” In 2014, the Brentano Quartet succeeded the Tokyo Quartet as Artists in Residence at Yale University, departing from their fourteen-year residency at Princeton University. The quartet also currently serves as the collaborative ensemble for the Van Cliburn International Piano Competition. The quartet has performed in the world’s most prestigious venues, including Carnegie Hall and Alice Tully Hall in New York; the Library of Congress in Washington; the Concertgebouw in Amsterdam; the Konzerthaus in Vienna; Suntory Hall in Tokyo; and the Sydney Opera House. -

The English Concert – Biography
The English Concert – Biography The English Concert is one of Europe’s leading chamber orchestras specialising in historically informed performance. Created by Trevor Pinnock in 1973, the orchestra appointed Harry Bicket as its Artistic Director in 2007. Bicket is renowned for his work with singers and vocal collaborators, including in recent seasons Lucy Crowe, Elizabeth Watts, Sarah Connolly, Joyce DiDonato, Alice Coote and Iestyn Davies. The English Concert has a wide touring brief and the 2014-15 season will see them appear both across the UK and abroad. Recent highlights include European and US tours with Alice Coote, Joyce DiDonato, David Daniels and Andreas Scholl as well as the orchestra’s first tour to mainland China. Harry Bicket directed The English Concert and Choir in Bach’s Mass in B Minor at the 2012 Leipzig Bachfest and later that year at the BBC proms, a performance that was televised for BBC4. Following the success of Handel’s Radamisto in New York 2013, Carnegie Hall has commissioned one Handel opera each season from The English Concert. Theodora followed in early 2014, which toured West Coast of the USA as well as the Théâtre des Champs Elysées Paris and the Barbican London followed by a critically acclaimed tour of Alcina in October 2014. Future seasons will see performances of Handel’s Hercules and Orlando. The English Concert’s discography includes more than 100 recordings with Trevor Pinnock for Deutsche Grammophon Archiv, and a series of critically acclaimed CDs for Harmonia Mundi with violinist Andrew Manze. Recordings with Harry Bicket have been widely praised, including Lucy Crowe’s debut solo recital, Il caro Sassone. -

BRITISH and COMMONWEALTH CONCERTOS from the NINETEENTH CENTURY to the PRESENT Sir Edward Elgar
BRITISH AND COMMONWEALTH CONCERTOS FROM THE NINETEENTH CENTURY TO THE PRESENT A Discography of CDs & LPs Prepared by Michael Herman Sir Edward Elgar (1857-1934) Born in Broadheath, Worcestershire, Elgar was the son of a music shop owner and received only private musical instruction. Despite this he is arguably England’s greatest composer some of whose orchestral music has traveled around the world more than any of his compatriots. In addition to the Conceros, his 3 Symphonies and Enigma Variations are his other orchestral masterpieces. His many other works for orchestra, including the Pomp and Circumstance Marches, Falstaff and Cockaigne Overture have been recorded numerous times. He was appointed Master of the King’s Musick in 1924. Piano Concerto (arranged by Robert Walker from sketches, drafts and recordings) (1913/2004) David Owen Norris (piano)/David Lloyd-Jones/BBC Concert Orchestra ( + Four Songs {orch. Haydn Wood}, Adieu, So Many True Princesses, Spanish Serenade, The Immortal Legions and Collins: Elegy in Memory of Edward Elgar) DUTTON EPOCH CDLX 7148 (2005) Violin Concerto in B minor, Op. 61 (1909-10) Salvatore Accardo (violin)/Richard Hickox/London Symphony Orchestra ( + Walton: Violin Concerto) BRILLIANT CLASSICS 9173 (2010) (original CD release: COLLINS CLASSICS COL 1338-2) (1992) Hugh Bean (violin)/Sir Charles Groves/Royal Liverpool Philharmonic Orchestra ( + Violin Sonata, Piano Quintet, String Quartet, Concert Allegro and Serenade) CLASSICS FOR PLEASURE CDCFP 585908-2 (2 CDs) (2004) (original LP release: HMV ASD2883) (1973) -

Music Collection News 015047800049 Selected New Cds
M USIC COLLECTION NEWS Winter, 2013 Greetings musicians! The library’s new resource, OneSearch, offers the opportunity to search for recordings in the CD collection simultaneously with Naxos Music Library as well as for scores. MC staff are ready to help you learn the ropes. The Music Collection continues to strive to meet the very diverse needs of faculty, staff, and students. I think the new materials featured in this issue reflect that diversity. —Amy Edmonds Music Librarian OneSearch: A New, Powerful Tool! In this issue: OneSearch is a research tool for looking up one topic in many sources simultaneously: New CDs 2 CardCat, WorldCat, and Ball State subscription databases, including Naxos Music Library. New DVDs 2 You can limit the results to books, scholarly journals, or compact disc, music record- ing (Naxos), or score. New on Naxos 2 The sample to the right Music Online shows the break-down of formats for a search of “Eroica Symphony.” Note New Books 3 that book reviews and newspaper articles are automatically excluded. You can also limit by New Scores 3 language, date, subject, and articles or books online. New Popular CDs 3 Bracken Library phone numbers: Music Collection: Educational Resources: 765-285-8188 765-285-5333 Featured Books, 4 Music Librarian: Reference: CDs and Scores 765-285-5065 765-285-1101 Page 2 Music Collection News 015047800049 Selected New CDs: Albéniz. Spanish Music for Mozart / Uchida (cond. & piano). Segovia: The Great Master Classical Guitar Piano Concertos Nos. 20 & 27 Compact Disc 21181 Compact Disc 21330 Compact Disc 21337 Shostakovich / Gergiev. Carter, E.