Thermographic Inspection of Internal Defects in Steel Structures: Analysis of Signal Processing Techniques in Pulsed Thermography
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

RADIOGRAPHY to Prepare Individuals to Become Registered Radiologic Technologists
RADIOGRAPHY To prepare individuals to become Registered Radiologic Technologists. THE WORKFORCE CAPITAL This two-year, advanced medical program trains students in radiography. Radiography uses radiation to produce images of tissues, organs, bones and vessels of the body. The radiographer is an essential member of the health care team who works in a variety of settings. Responsibili- ties include accurately positioning the patient, producing quality diagnostic images, maintaining equipment and keeping computerized records. This certificate program of specialized training focuses on each of these responsibilities. Graduates are eligible to apply for the national credential examination to become a registered technologist in radiography, RT(R). Contact Student Services for current tuition rates and enrollment information. 580.242.2750 Mission, Goals, and Student Learning Outcomes Program Effectiveness Data Radiography Program Guidelines (Policies and Procedures) “The programs at Autry prepare you for the workforce with no extra training needed after graduation.” – Kenedy S. autrytech.edu ENDLESS POSSIBILITIES 1201 West Willow | Enid, Oklahoma, 73703 | 580.242.2750 | autrytech.edu COURSE LENGTH Twenty-four-month daytime program î August-July î Monday-Friday Academic hours: 8:15am-3:45pm Clinical hours: Eight-hour shifts between 7am-5pm with some ADMISSION PROCEDURES evening assignments required Applicants should contact Student Services at Autry Technology Center to request an information/application packet. Applicants who have a completed application on file and who have met entrance requirements will be considered for the program. Meeting ADULT IN-DISTRICT COSTS the requirements does not guarantee admission to the program. Qualified applicants will be contacted for an interview, and class Year One: $2732 (Additional cost of books and supplies approx: $1820) selection will be determined by the admissions committee. -

ACR–SPR-STR Practice Parameter for the Performance of Chest Radiography
The American College of Radiology, with more than 30,000 members, is the principal organization of radiologists, radiation oncologists, and clinical medical physicists in the United States. The College is a nonprofit professional society whose primary purposes are to advance the science of radiology, improve radiologic services to the patient, study the socioeconomic aspects of the practice of radiology, and encourage continuing education for radiologists, radiation oncologists, medical physicists, and persons practicing in allied professional fields. The American College of Radiology will periodically define new practice parameters and technical standards for radiologic practice to help advance the science of radiology and to improve the quality of service to patients throughout the United States. Existing practice parameters and technical standards will be reviewed for revision or renewal, as appropriate, on their fifth anniversary or sooner, if indicated. Each practice parameter and technical standard, representing a policy statement by the College, has undergone a thorough consensus process in which it has been subjected to extensive review and approval. The practice parameters and technical standards recognize that the safe and effective use of diagnostic and therapeutic radiology requires specific training, skills, and techniques, as described in each document. Reproduction or modification of the published practice parameter and technical standard by those entities not providing these services is not authorized. Revised 2017 (Resolution 2)* ACR–SPR–STR PRACTICE PARAMETER FOR THE PERFORMANCE OF CHEST RADIOGRAPHY PREAMBLE This document is an educational tool designed to assist practitioners in providing appropriate radiologic care for patients. Practice Parameters and Technical Standards are not inflexible rules or requirements of practice and are not intended, nor should they be used, to establish a legal standard of care1. -

Estimation of the Collective Effective Dose to the Population from Medical X-Ray Examinations in Finland
Estimation of the collective effective dose to the population from medical x-ray examinations in Finland Petra Tenkanen-Rautakoskia, Hannu Järvinena, Ritva Blya aRadiation and Nuclear Safety Authority (STUK), PL 14, 00880 Helsinki, Finland Abstract. The collective effective dose to the population from all x-ray examinations in Finland in 2005 was estimated. The numbers of x-ray examinations were collected by a questionnaire to the health care units (response rate 100 %). The effective doses in plain radiography were calculated using a Monte Carlo based program (PCXMC), as average values for selected health care units. For computed tomography (CT), weighted dose length product (DLPw) in a standard phantom was measured for routine CT protocols of four body regions, for 80 % of CT scanners including all types. The effective doses were calculated from DPLw values using published conversion factors. For contrast-enhanced radiology and interventional radiology, the effective dose was estimated mainly by using published DAP values and conversion factors for given body regions. About 733 examinations per 1000 inhabitants (excluding dental) were made in 2005, slightly less than in 2000. The proportions of plain radiography, computed tomography, contrast-enhanced radiography and interventional procedures were about 92, 7, 1 and 1 %, respectively. From 2000, the frequencies (number of examinations per 1000 inhabitants) of plain radiography and contrast-enhanced radiography have decreased about 8 and 33 %, respectively, while the frequencies of CT and interventional radiology have increased about 28 and 38 %, respectively. The population dose from all x-ray examinations is about 0,43 mSv per person (in 1997 0,5 mSv). -
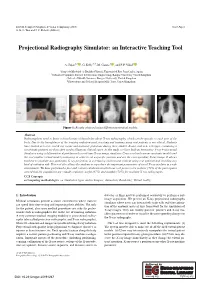
Projectional Radiography Simulator: an Interactive Teaching Tool
EG UK Computer Graphics & Visual Computing (2019) Short Paper G. K. L. Tam and J. C. Roberts (Editors) Projectional Radiography Simulator: an Interactive Teaching Tool A. Sujar1,2 , G. Kelly3,4, M. García1 , and F. P. Vidal2 1Grupo de Modelado y Realidad Virtual, Universidad Rey Juan Carlos, Spain 2School of Computer Science & Electronic Engineering, Bangor University United Kingdom 3School of Health Sciences, Bangor University, United Kingdom 4Shrewsbury and Telford Hospital NHS Trust, United Kingdom Figure 1: Results obtained using different anatomical models. Abstract Radiographers need to know a broad range of knowledge about X-ray radiography, which can be specific to each part of the body. Due to the harmfulness of the ionising radiation used, teaching and training using real patients is not ethical. Students have limited access to real X-ray rooms and anatomic phantoms during their studies. Books, and now web apps, containing a set of static pictures are then often used to illustrate clinical cases. In this study, we have built an Interactive X-ray Projectional Simulator using a deformation algorithm with a real-time X-ray image simulator. Users can load various anatomic models and the tool enables virtual model positioning in order to set a specific position and see the corresponding X-ray image. It allows teachers to simulate any particular X-ray projection in a lecturing environment without using real patients and avoiding any kind of radiation risk. This tool also allows the students to reproduce the important parameters of a real X-ray machine in a safe environment. We have performed a face and content validation in which our tool proves to be realistic (72% of the participants agreed that the simulations are visually realistic), useful (67%) and suitable (78%) for teaching X-ray radiography. -

Download Article (PDF)
Current Directions in Biomedical Engineering 2015; 1:257–260 Thomas Homann*, Axel Boese, Sylvia Glaßer, Martin Skalej, and Oliver Beuing Intravascular optical coherence tomography (OCT) as an additional tool for the assessment of stent structures Abstract: Evaluation of the vascular stent position, shape cases an additional imaging of the implants by OCT would and correct expansion has a high relevance in therapy be benecial. In our study, we determined the ability of and diagnosis. Hence, the wall apposition in vessel areas OCT to image structural information of dierent vascular with diering diameters and the appearance of torsions or stents in a phantom study. structural defects of the implant body caused by catheter based device dropping are of special interest. Neurovascu- lar implants like braided ow diverter and laser cut stents 2 Materials and methods consist of metal struts and wires with diameters of about 40 µm. Depending on the implants material composition, A plastic model with bores of dierent diameters for the in- visibility is poor with conventional 2D X-ray uoroscopic take of 3 vascular implants was manufactured (see Figure and radiographic imaging. The metal structures of the im- 1). The model has a geometrical extend of 80 mm×50 mm× plants also lead to artifacts in 3D X-ray images and can 15 mm and a straight course of the bores. A translucent hamper the assessment of the device position. We inves- plastic material was selected for a low absorption of near tigated intravascular optical coherence tomography (OCT) infrared light generated by the OCT system. Objects of in- as a new imaging tool for the evaluation of the vascular vestigation were 3 vascular stents with dierent geometri- stent position, its shape and its correct expansion for 3 dif- cal and structural properties (see Table 1). -

X-Ray (Radiography) - Bone Bone X-Ray Uses a Very Small Dose of Ionizing Radiation to Produce Pictures of Any Bone in the Body
X-ray (Radiography) - Bone Bone x-ray uses a very small dose of ionizing radiation to produce pictures of any bone in the body. It is commonly used to diagnose fractured bones or joint dislocation. Bone x-rays are the fastest and easiest way for your doctor to view and assess bone fractures, injuries and joint abnormalities. This exam requires little to no special preparation. Tell your doctor and the technologist if there is any possibility you are pregnant. Leave jewelry at home and wear loose, comfortable clothing. You may be asked to wear a gown. What is Bone X-ray (Radiography)? An x-ray exam helps doctors diagnose and treat medical conditions. It exposes you to a small dose of ionizing radiation to produce pictures of the inside of the body. X-rays are the oldest and most often used form of medical imaging. A bone x-ray makes images of any bone in the body, including the hand, wrist, arm, elbow, shoulder, spine, pelvis, hip, thigh, knee, leg (shin), ankle or foot. What are some common uses of the procedure? A bone x-ray is used to: diagnose fractured bones or joint dislocation. demonstrate proper alignment and stabilization of bony fragments following treatment of a fracture. guide orthopedic surgery, such as spine repair/fusion, joint replacement and fracture reductions. look for injury, infection, arthritis, abnormal bone growths and bony changes seen in metabolic conditions. assist in the detection and diagnosis of bone cancer. locate foreign objects in soft tissues around or in bones. How should I prepare? Most bone x-rays require no special preparation. -

The ASRT Practice Standards for Medical Imaging and Radiation Therapy
The ASRT Practice Standards for Medical Imaging and Radiation Therapy Sonography ©2019 American Society of Radiologic Technologists. All rights reserved. Reprinting all or part of this document is prohibited without advance written permission of the ASRT. Send reprint requests to the ASRT Publications Department, 15000 Central Ave. SE, Albuquerque, NM 87123-3909. Effective June 23, 2019 Table of Contents Preface .......................................................................................................................................................... 1 Format ....................................................................................................................................................... 1 Introduction .................................................................................................................................................. 3 Definition .................................................................................................................................................. 3 Education and Certification ...................................................................................................................... 5 Medical Imaging and Radiation Therapy Scope of Practice .......................................................................... 6 Standards ...................................................................................................................................................... 8 Standard One – Assessment .................................................................................................................... -

Radiography Program
Radiography Program Program Description The Radiography (X-ray) Program at Tulsa Community College is designed to prepare students with the knowledge and skills to function as medical radiographers. The program is nationally accredited by the Joint Review Committee on Education in Radiologic Technology. Medical Radiographers/Radiologic Technologists are the medical personnel who perform diagnostic imaging examinations. Radiographers use x-rays to produce black and white images of anatomy. These images are captured on film, computer or videotape. Radiographers are educated in anatomy, patient positioning, examination techniques, equipment protocols, radiation safety, radiation protection and basic patient care. Radiographers often specialize in areas of CT, MRI, Mammography, Cardiovascular Technology, Quality Control, Management and Education. Radiographers work closely with radiologists, physicians who interpret medical images to either diagnose or rule out disease or injury. Program Information Degree Awarded: Associate Degree in Applied Science The Radiography (X-ray) Program admits a new class each year beginning in June (summer term). The number of students admitted to the class is determined by the number of clinical training sites available to place students, which is usually between 30-35 students. Radiography is a two-year (six-semester) program consisting of 48 credit hours of Radiography courses (didactic and clinical) and 22 hours of related general education courses. Lecture and clinical courses run concurrently throughout the two years. Upon completion of the program, graduates receive an Associate in Applied Science (AAS) degree, and are eligible to apply for examination by the American Registry of Radiologic Technologists (ARRT) in Radiography (R). Clinical education classes consist of eight-hour shifts for two to three days per week in the assigned clinical education center. -

THE TERMOGRAPHIC ANALYSIS of the WELDING by TIG M.Sc., Eng
SCIENTIFIC PROCEEDINGS XI INTERNATIONAL CONGRESS "MACHINES, TECHNOLОGIES, MATERIALS" 2014 ISSN 1310-3946 THE TERMOGRAPHIC ANALYSIS OF THE WELDING BY TIG M.Sc., Eng. Maś K., M.Sc. Woźny M., PhD. Marchewka M. , PhD. Płoch D. and Prof. Dr.Sheregii E.M. Centre for Microelectronics and Nanotechnology, University of Rzeszow, Poland [email protected] Abstract: Thermography measurements allow to detect the defects that may appear on a joint at welding of components. Energy pulse generated by a xenon lamp with adequate power in a short period of time is sufficient for thermal excitation and enables to register the temperature distribution using the thermography high resolution camera FLIR SC7000. The impulse with 6kJ energy and 6ms time generate sufficient power to measure the temperature distribution on the surface of the weld tested. During cooling the temperature of the area with defect changes more slowly than in the areas without defects, because of to the less intense heat dissipation. This allows the registration of defects in welds "on-line" at the production process. Material used for analysis detection of defects in the welded joints is Inconel 718, stainless steel 410 and stainless steel 321. The peak energy which flow throw the samples with defects in the welded joints its completely or partially blocked. It cause different temperature distribution on the surface in the places where the connection discontinuity take place. Keywords: THERMOGRAPHY, DEFECTS, WELDING, NDT 1. Introduction therefore, X-rays and gamma rays can be used to show discontinuities and inclusions within the opaque material. The Welded joints and padding layers are subjected to control permanent film record of the internal conditions will show the basic processes through the use of non-destructive testing methods to information by which the weld reliability and credibility could be ensure a high quality semi-finished and finished products [1-3]. -

Diagnostic Radiology Physics Diagnostic This Publication Provides a Comprehensive Review of Topics Relevant to Diagnostic Radiology Physics
A Handbook for Teachers and Students A Handbook for Teachers Diagnostic Diagnostic This publication provides a comprehensive review of topics relevant to diagnostic radiology physics. It is intended to provide the basis for the education of medical physicists in the field of diagnostic radiology. Bringing together the work of 41 authors and reviewers from 12 countries, the handbook covers a broad range of topics including radiation physics, dosimetry and Radiology instrumentation, image quality and image perception, imaging modality specific topics, recent advances in digital techniques, and radiation biology and protection. It is not designed to replace the large number of textbooks available on many aspects of diagnostic radiology physics, but is expected Radiology Physics Physics to fill a gap in the teaching material for medical radiation physics in imaging, providing in a single manageable volume the broadest coverage of topics currently available. The handbook has been endorsed by several international professional bodies and will be of value to those preparing for their certification A Handbook for as medical physicists, radiologists and diagnostic radiographers. Teachers and Students D.R. Dance S. Christofides A.D.A. Maidment I.D. McLean K.H. Ng Technical Editors International Atomic Energy Agency Vienna ISBN 978–92–0–131010–1 1 @ DIAGNOSTIC RADIOLOGY PHYSICS: A HANDBOOK FOR TEACHERS AND STUDENTS The following States are Members of the International Atomic Energy Agency: AFGHANISTAN GHANA OMAN ALBANIA GREECE PAKISTAN ALGERIA GUATEMALA -

Radiation and Your Patient: a Guide for Medical Practitioners
RADIATION AND YOUR PATIENT: A GUIDE FOR MEDICAL PRACTITIONERS A web module produced by Committee 3 of the International Commission on Radiological Protection (ICRP) What is the purpose of this document ? In the past 100 years, diagnostic radiology, nuclear medicine and radiation therapy have evolved from the original crude practices to advanced techniques that form an essential tool for all branches and specialties of medicine. The inherent properties of ionising radiation provide many benefits but also may cause potential harm. In the practice of medicine, there must be a judgement made concerning the benefit/risk ratio. This requires not only knowledge of medicine but also of the radiation risks. This document is designed to provide basic information on radiation mechanisms, the dose from various medical radiation sources, the magnitude and type of risk, as well as answers to commonly asked questions (e.g radiation and pregnancy). As a matter of ease in reading, the text is in a question and answer format. Interventional cardiologists, radiologists, orthopaedic and vascular surgeons and others, who actually operate medical x-ray equipment or use radiation sources, should possess more information on proper technique and dose management than is contained here. However, this text may provide a useful starting point. The most common ionising radiations used in medicine are X, gamma, beta rays and electrons. Ionising radiation is only one part of the electromagnetic spectrum. There are numerous other radiations (e.g. visible light, infrared waves, high frequency and radiofrequency electromagnetic waves) that do not posses the ability to ionize atoms of the absorbing matter. -

Radiography Library Resource Guide a Selected List of Resources
Radiography Library Resource Guide A Selected List of Resources Library Hours Contact us Monday – Friday 7:30 am – 10:00 pm Website http://www.ntc.edu/library Saturday – Sunday 9:00 am – 3:00 pm Email [email protected] Phone 715.803.1115 SUGGESTED SEARCH TERMS Angiography Nuclear Medicine Bone density Physics Computed Tomography Positron Emission Tomography Contrast agents Radiation biology Diagnostic Radiology Radiation dosimetry Diagnostic ultrasound Radiation protection Digital radiography Radiation protection Interventional radiologic Radiographic positioning procedures Radiography Direct radiography Roentgen variants Fluoroscopy Sonography Incident beam SPECT Magnetic Resonance Imaging Ultrasonography Mammography Ultrasound Imaging Modalities X-ray imaging Library 1st floor: 2012 - Present Nuclear Magnetic Resonance X-ray production CALL NUMBERS (LIBRARY 2nd FLOOR) 174.2 Ethics 530 Physics 611 Human Anatomy 616 Radiography BOOKS AT THE LIBRARY 10/21/2016 1 DATABASES • Academic Search Premier • Gale Virtual Reference Books (GVRL) • AHFS Consumer Medication Information • Health Source: Nursing/Academic Edition • Alt HealthWatch • MasterFILE Premier • CINAHL • MEDLINE • Credo Reference • ProQuest Nursing and Allied Health Source • Ebrary • ProQuest Research Library • • Films on Demand PubMed Central • SpringerLink ELECTRONIC BOOKS & SPECIALIZED REFERENCE SOURCES • GVRL (Gale Virtual Reference Library) o Arthritis Sourcebook (2010) o Child Abuse Sourcebook (2013) o Gale Encyclopedia of Cancer (2010) o Gale Encyclopedia of Genetic Disorders