Units and Prefixes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -
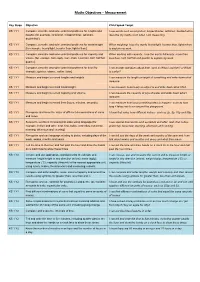
Maths Objectives – Measurement
Maths Objectives – Measurement Key Stage Objective Child Speak Target KS 1 Y1 Compare, describe and solve practical problems for lengths and I use words such as long/short, longer/shorter, tall/short, double/half to heights [for example, long/short, longer/shorter, tall/short, describe my maths work when I am measuring. double/half]. KS 1 Y1 Compare, describe and solve practical problems for mass/weight When weighing, I use the words heavy/light, heavier than, lighter than [for example, heavy/light, heavier than, lighter than]. to explain my work. KS 1 Y1 Compare, describe and solve practical problems for capacity and When working with capacity, I use the words full/empty, more than, volume [for example, full/empty, more than, less than, half, half full, less than, half, half full and quarter to explain my work. quarter]. KS 1 Y1 Compare, describe and solve practical problems for time [for I can answer questions about time, such as Who is quicker? or What example, quicker, slower, earlier, later]. is earlier? KS 1 Y1 Measure and begin to record lengths and heights. I can measure the length or height of something and write down what measure. KS 1 Y1 Measure and begin to record mass/weight. I can measure how heavy an object is and write down what I find. KS 1 Y1 Measure and begin to record capacity and volume. I can measure the capacity of jugs of water and write down what I measure. KS 1 Y1 Measure and begin to record time (hours, minutes, seconds). I can measure how long something takes to happen - such as how long it takes me to run around the playground. -

Standard Caption Abberaviation
TECHNICAL SHEET Page 1 of 2 STANDARD CAPTION ABBREVIATIONS Ref: T120 – Rev 10 – March 02 The abbreviated captions listed are used on all instruments except those made to ANSI C39. 1-19. Captions for special scales to customers’ requirements must comply with BS EN 60051, unless otherwise specified at time of ordering. * DENOTES captions applied at no extra cost. Other captions on request. ELECTRICAL UNITS UNIT SYMBOL UNIT SYMBOL Direct Current dc Watt W * Alternating current ac Milliwatts mW * Amps A * Kilowatts kW * Microamps µA * Megawatts MW * Milliamps mA * Vars VAr * Kiloamps kA * Kilovars kVAr * Millivolts mV * Voltamperes VA * Kilovolts kV * Kilovoltamperes kVA * Cycles Hz * Megavoltamperes MVA * Power factor cos∅ * Ohms Ω * Synchroscope SYNCHROSCOPE * Siemens S Micromhos µmho MECHANICAL UNITS Inches in Micrometre (micron) µm Square inches in2 Millimetre mm Cubic inches in3 Square millimetres mm2 Inches per second in/s * Cubic millimetres mm3 Inches per minute in/min * Millimetres per second mm/s * Inches per hour in/h * Millimetres per minute mm/min * Inches of mercury in hg Millimetres per hour mm/h * Feet ft Millimetres of mercury mm Hg Square feet ft2 Centimetre cm Cubic feet ft3 Square centimetres cm2 Feet per second ft/s * Cubic centimetres cm3 Feet per minute ft/min * Cubic centimetres per min cm3/min Feet per hour ft/h * Centimetres per second cm/s * Foot pound ft lb Centimetres per minute cm/min * Foot pound force ft lbf Centimetres per hour cm/h * Hours h Decimetre dm Yards yd Square decimetre dm2 Square yards yd2 Cubic -

Using Mathematical Operations to Convert Metric Linear Units
Converting Metric Linear Units Using Mathematical Operations to Convert Metric Linear Units Converting Larger to Smaller Units To convert from larger to smaller metric linear units, multiply by 10 for each step downward on the metric staircase. Metric Staircase Use this ACRONYM to help you remember the kilo King order of the units: hecto Henry’s King Henry’s deca Daughter Daughter base unit Betty Betty deci Detested Detested centi Counting Counting milli Money Money Examples A) How many cm in 1 m? m to cm is 2 steps Metric Staircase 1 m = 10 × 10 = 100 cm There are 100 cm in 1 m. m dm B) How many mm in 1 m? cm m to mm is 3 steps mm 1 m = 10 × 10 × 10 = 1000 mm There are 1000 mm in 1 m. Remember that 10 × 10 × 10 = 1000 10 × 10 = 100 C) How many mm in 4.2 m? 4.2 × 10 × 10 × 10 = 4200 mm OR 4.2 × 1000 = 4200 mm There are 4200 mm in 4.2 m. Knowledge and Employability Studio Shape and Space: Measurement: Mathematics Linear Measurement: ©Alberta Education, Alberta, Canada (www.LearnAlberta.ca) Converting Metric Linear Units 1/12 D) For every kilometre you travel in a car or school bus, you are travelling 1000 metres. How many metres in 69.7 kilometres? km to m is 3 steps Metric Staircase 10 × 10 × 10 = 1000 m There are 1000 m in 1 km. km 69.7 × 10 × 10 × 10 = 69 700 m hm OR dam 69.7 × 1000 = 69 700 m m There are 69 700 m in 69.7 km. -

Introducyon to the Metric System Bemeasurement, Provips0.Nformal, 'Hands-On Experiences For.The Stud4tts
'DOCUMENT RESUME ED 13A 755 084 CE 009 744 AUTHOR Cáoper, Gloria S., Ed.; Mag4,sos Joel B., Ed. TITLE q Met,rits for.Theatrical COstum g: ° INSTITUTION Ohio State Univ., Columbus. enter for Vocational Education. SPONS AGENCY Ohio State Univ., Columbus. Center for.Vocational Education. PUB DATE 76 4. CONTRACT - OEC-0-74-9335 NOTE 59p.1 For a. related docuMent see CE 009 736-790 EDRS PRICE 10-$0.8.3 C-$3.50 Plus Pdstage: DESCRIPTORS *Curriculu; Fine Arts; Instructional Materials; Learning. ctivities;xMeasurement.Instrnments; *Metric, System; S condary Education; Teaching Technigue8; *Theater AttS; Units of Sttidy (Subject Fields) ; , *Vocational Eiducation- IDENTIFIERS Costumes (Theatrical) AESTRACT . Desigliedto meet tbe job-related m4triceasgrement needs of theatrical costuming students,'thiS instructio11 alpickage is one of live-for the arts and-huminities occupations cluster, part of aset b*: 55 packages for:metric instrection in diftepent occupations.. .The package is in'tended for students who already knovthe occupaiiOnal terminology, measurement terms, and tools currently in use. Each of the five units in this instructional package.contains performance' objectiveS, learning:Activities, and'supporting information in-the form of text,.exertises,- ard tabled. In. add±tion, Suggested teaching technigueS are included. At the'back of the package*are objective-base'd:e"luation items, a-page of answers to' the exercises,and tests, a list of metric materials ,needed for the ,activities4 references,- and a/list of supPliers.t The_material is Y- designed. to accVmodate awariety of.individual teacting,:and learning k. styles, e.g., in,dependent:study, small group, or whole-class Setivity. -

The Astronomical Units
The astronomical units N. Capitaine and B. Guinot November 5, 2018 SYRTE, Observatoire de Paris, CNRS, UPMC 61, avenue de l’Observatoire, 75014 Paris, France e-mail: [email protected]; [email protected] Abstract The IAU-1976 System of astronomical constants includes three astronomical units (i.e. for time, mass and length). This paper reports on the status of the astronomical unit of length (ua) and mass (MSun) within the context of the recent IAU Resolutions on reference systems and the use of modern observations in the solar system. We especially look at a possible re-definition of the ua as an astronomical unit of length defined trough a fixed relation to the SI metre by a defining number. Keywords: reference systems, astronomical constants, numerical standards 1. INTRODUCTION The IAU-1976 System of astronomical constants includes three astronomical units, namely the astronomical unit of time, the day, D, which is related to the SI by a defining number (D=86400 s), the astronomical unit of mass, i.e. the mass of the Sun, MSun, and the astronomical unit of length, ua. Questions related to the definition, numerical value and role of the astronomical units have been discussed in a number of papers, e.g. (Capitaine & Guinot 1995), (Guinot 1995), (Huang et al. 1995), (Standish 1995, 2004) and (Klioner 2007). The aim of this paper is to report on recent views on these topics. The role of the astronomical unit of time, which (as is the Julian century of 36 525 days) is to provide a unit of time of convenient size for astronomy, does not need further discussion. -

Orders of Magnitude (Length) - Wikipedia
03/08/2018 Orders of magnitude (length) - Wikipedia Orders of magnitude (length) The following are examples of orders of magnitude for different lengths. Contents Overview Detailed list Subatomic Atomic to cellular Cellular to human scale Human to astronomical scale Astronomical less than 10 yoctometres 10 yoctometres 100 yoctometres 1 zeptometre 10 zeptometres 100 zeptometres 1 attometre 10 attometres 100 attometres 1 femtometre 10 femtometres 100 femtometres 1 picometre 10 picometres 100 picometres 1 nanometre 10 nanometres 100 nanometres 1 micrometre 10 micrometres 100 micrometres 1 millimetre 1 centimetre 1 decimetre Conversions Wavelengths Human-defined scales and structures Nature Astronomical 1 metre Conversions https://en.wikipedia.org/wiki/Orders_of_magnitude_(length) 1/44 03/08/2018 Orders of magnitude (length) - Wikipedia Human-defined scales and structures Sports Nature Astronomical 1 decametre Conversions Human-defined scales and structures Sports Nature Astronomical 1 hectometre Conversions Human-defined scales and structures Sports Nature Astronomical 1 kilometre Conversions Human-defined scales and structures Geographical Astronomical 10 kilometres Conversions Sports Human-defined scales and structures Geographical Astronomical 100 kilometres Conversions Human-defined scales and structures Geographical Astronomical 1 megametre Conversions Human-defined scales and structures Sports Geographical Astronomical 10 megametres Conversions Human-defined scales and structures Geographical Astronomical 100 megametres 1 gigametre -
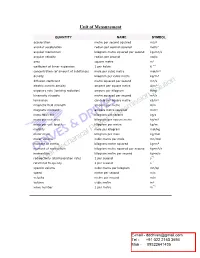
Unit of Measurement
Unit of Measurement QUANTITY NAME SYMBOL acceleration metre per second squared m/s² angular acceleration radian per second squared rad/s² angular momentum kilogram metre squared per second kg•m²/s angular velocity radian per second rad/s area square metre m² cœfficient of linear expansion 1 per kelvin K ¯¹ concentration (of amount of substance) mole per cubic metre mol/m³ density kilogram per cubic metre kg/m³ diffusion cœfficient metre squared per second m²/s electric current density ampere per square metre A/m² exposure rate (ionising radiation) ampere per kilogram A/kg kinematic viscosity metre squared per second m²/s luminance candela per square metre cd/m² magnetic field strength ampere per metre A/m magnetic moment ampere metre squared A•m² mass flow rate kilogram per second kg/s mass per unit area kilogram per square metre kg/m² mass per unit length kilogram per metre kg/m molality mole per kilogram mol/kg molar mass kilogram per mole kg/mol molar volume cubic metre per mole m³/mol moment of inertia kilogram metre squared kg•m² moment of momentum kilogram metre squared per second kg•m²/s momentum kilogram metre per second kg•m/s radioactivity (disintergration rate) 1 per second s¯¹ rotational frequency 1 per second s¯¹ specific volume cubic metre per kilogram m³/kg speed metre per second m/s velocity metre per second m/s volume cubic metre m³ wave number 1 per metre m¯¹ SI units and Additional QUANTITY NAME SYMBOL units absorbed dose joule per kilogram J/kg m²•s¯² watt per meter squared coefficient of heat transfer W/m²•K kg•s¯³•K¯¹ -

SI Base Units
463 Appendix I SI base units 1 THE SEVEN BASE UNITS IN THE INTERNatioNAL SYSTEM OF UNITS (SI) Quantity Name of Symbol base SI Unit Length metre m Mass kilogram kg Time second s Electric current ampere A Thermodynamic temperature kelvin K Amount of substance mole mol Luminous intensity candela cd 2 SOME DERIVED SI UNITS WITH THEIR SYMBOL/DerivatioN Quantity Common Unit Symbol Derivation symbol Term Term Length a, b, c metre m SI base unit Area A square metre m² Volume V cubic metre m³ Mass m kilogram kg SI base unit Density r (rho) kilogram per cubic metre kg/m³ Force F newton N 1 N = 1 kgm/s2 Weight force W newton N 9.80665 N = 1 kgf Time t second s SI base unit Velocity v metre per second m/s Acceleration a metre per second per second m/s2 Frequency (cycles per second) f hertz Hz 1 Hz = 1 c/s Bending moment (torque) M newton metre Nm Pressure P, F newton per square metre Pa (N/m²) 1 MN/m² = 1 N/mm² Stress σ (sigma) newton per square metre Pa (N/m²) Work, energy W joule J 1 J = 1 Nm Power P watt W 1 W = 1 J/s Quantity of heat Q joule J Thermodynamic temperature T kelvin K SI base unit Specific heat capacity c joule per kilogram degree kelvin J/ kg × K Thermal conductivity k watt per metre degree kelvin W/m × K Coefficient of heat U watt per square metre kelvin w/ m² × K 464 Rural structures in the tropics: design and development 3 MUltiples AND SUB MUltiples OF SI–UNITS COMMONLY USED IN CONSTRUCTION THEORY Factor Prefix Symbol 106 mega M 103 kilo k (102 hecto h) (10 deca da) (10-1 deci d) (10-2 centi c) 10-3 milli m 10-6 micro u Prefix in brackets should be avoided. -

Brief History and Use of the ENGLISH and METRIC SYSTEMS of MEASUREMENT with a CHART of the MODERNIZED METRIC SYSTEM
AUG 13 1971 -^4 UNITED STATES DEPARTMENT OF COMMERCE 161670 C. R. SMITH, Secretary NATIONAL BUREAU OF STANDARDS / a. v. astin, Director Special Publication 304A. Issued 1968. lUj h Brief History and Use of THE ENGLISH AND METRIC SYSTEMS OF MEASUREMENT with a CHART OF THE MODERNIZED METRIC SYSTEM "Weights and measures may be ranked among the necessaries of life to every individual of human society. They enter into the eco- nomical arrangements and daily concerns of every family. They are necessary to every occupation of human industry; to the distribution and security of every species of property; to every transaction of trade and commerce ; to the labors of the husbandman ; to the in- genuity of the artificer; to the studies of the philosopher ; to the researches of the antiquarian, to the navigation of the mariner, and the marches of the soldier; to all the exchanges of peace, and all the operations of war." —JOHN QUINCY ADAMS When the American Colonies sepa- sembly of France on May 8, 1790, of the length of a great circle of the rated from the mother country to to enact a decree, sanctioned by Louis earth. This idea found favor with the assume among the nations of the XVI, which called upon the French French philosophers at the time of the earth a separate and individual sta- Academy of Sciences in concert with French Revolution, men who were tion, they retained, among other the Royal Society of London to "de- generally opposed to any vestige of things, the weights and measures duce an invariable standard for all of monarchical authority and preferred that had been used when they were the measures and all weights." Hav- a standard based on a constant of colonies, namely, the weights and ing already an adequate system of nature. -
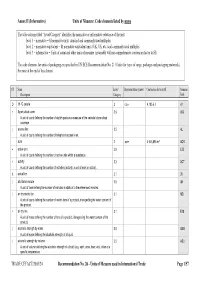
Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product. -
Linear Measures: the Metric System
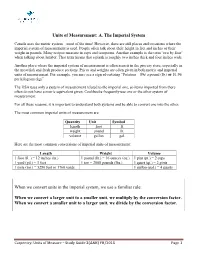
Units of Measurement: A. The Imperial System Canada uses the metric system – most of the time! However, there are still places and occasions where the imperial system of measurement is used. People often talk about their height in feet and inches or their weight in pounds. Many recipes measure in cups and teaspoons. Another example is the term ‘two by four’ when talking about lumber. That term means that a plank is roughly two inches thick and four inches wide. Another place where the imperial system of measurement is often seen is in the grocery store, especially in the meat/fish and fresh produce sections. Prices and weights are often given in both metric and imperial units of measurement. For example, you may see a sign advertising “Potatoes – 89¢ a pound (lb.) or $1.96 per kilogram (kg)”. The USA uses only a system of measurement related to the imperial one, so items imported from there often do not have a metric equivalent given. Cookbooks frequently use one or the other system of measurement. For all these reasons, it is important to understand both systems and be able to convert one into the other. The most common imperial units of measurement are: Quantity Unit Symbol length foot ft. weight pound lb. volume gallon gal. Here are the most common conversions of imperial units of measurement: Length Weight Volume 1 foot (ft. ) = 12 inches (in.) 1 pound (lb.) = 16 ounces (oz.) 1 pint (pt.) = 2 cups 1 yard (yd.) = 3 feet 1 ton = 2000 pounds (lbs.) 1 quart (qt.) = 2 pints 1 mile (mi.) = 5280 feet or 1760 yards 1 gallon (gal.) = 4 quarts When we convert units in the imperial system, we use a familiar rule: When we convert a larger unit to a smaller unit, we multiply by the conversion factor.