DOCSLIB.ORG

Brief History and Use of the ENGLISH and METRIC SYSTEMS of MEASUREMENT with a CHART of the MODERNIZED METRIC SYSTEM

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Brief History and Use of the ENGLISH and METRIC SYSTEMS of MEASUREMENT with a CHART of the MODERNIZED METRIC SYSTEM AUG 13 1971 -^4 UNITED STATES DEPARTMENT OF COMMERCE 161670 C. R. SMITH, Secretary NATIONAL BUREAU OF STANDARDS / a. v. astin, Director Special Publication 304A. Issued 1968. lUj h Brief History and Use of THE ENGLISH AND METRIC SYSTEMS OF MEASUREMENT with a CHART OF THE MODERNIZED METRIC SYSTEM "Weights and measures may be ranked among the necessaries of life to every individual of human society. They enter into the eco- nomical arrangements and daily concerns of every family. They are necessary to every occupation of human industry; to the distribution and security of every species of property; to every transaction of trade and commerce ; to the labors of the husbandman ; to the in- genuity of the artificer; to the studies of the philosopher ; to the researches of the antiquarian, to the navigation of the mariner, and the marches of the soldier; to all the exchanges of peace, and all the operations of war." —JOHN QUINCY ADAMS When the American Colonies sepa- sembly of France on May 8, 1790, of the length of a great circle of the rated from the mother country to to enact a decree, sanctioned by Louis earth. This idea found favor with the assume among the nations of the XVI, which called upon the French French philosophers at the time of the earth a separate and individual sta- Academy of Sciences in concert with French Revolution, men who were tion, they retained, among other the Royal Society of London to "de- generally opposed to any vestige of things, the weights and measures duce an invariable standard for all of monarchical authority and preferred that had been used when they were the measures and all weights." Hav- a standard based on a constant of colonies, namely, the weights and ing already an adequate system of nature. measures of England. It is probable weights and measures, the English The French Academy assigned the that these were at that time the most were not interested in the French name metre (meter), from the Greek firmly established and widely used undertaking, so the French proceeded metron, a measure, to the unit of weights and measures in the world. with their endeavor alone. The result length which was supposed to be one England a highly coherent nation, is what is known as the metric system. ten millionth of the distance from separated by sea from many of the The metric system was conceived the north pole to the equator, along turmoils of the European continent, as a measurement system to the base the meridian running near Dunkirk, had long before established stand- ten: that is, the units of the system, Paris, and Barcelona. An attempt was ards for weights and measures that their multiples, and submultiples made to measure this meridian from have remained essentially unchanged should be related to each other by northern France to southern France, up to the present time. The yard, simple factors of ten. This is a great from which the true distance from established by Henry II, differs only convenience because it conforms to the pole to the equator could be by about 1 part in a thousand from our common system for numerical no- calculated. The best techniques then the yard of today. The pound of tation, which is also a base ten system. available were used. Although the op- Queen Elizabeth I shows similar Thus to convert between units, their erations were carried out during a agreement with the present avoir- multiples, and submultiples. it is not politically disturbed time, the results dupois pound. necessary to perform a difficult mul- were in error only by about 2000 No such uniformity of weights and tiplication or division process, but meters, a remarkable achievement in measures existed on the European simply to shift the decimal point. those days. continent. Weights and measures dif- The system seems to have been first Meanwhile the National Assembly fered not only from country to coun- proposed by Gabriel Mouton, a vicar had preempted the geodetic survey, try, but even from town to town and of Lyons, France, in the late 17th cen- upon which the meter was to be based, from one trade to another. This lack tury. He proposed to define the unit and established a provisional meter. of uniformity led the National As- of length for the system as a fraction The unit of mass called the gram was For sale by the Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402 — Price 20 cents 1 0; The Modernized Metric Syt M E 1 8 i 7 9 1 0 Centimeter-! j 1 2 | 4 LLuJ,j,,ii,l!d,.,i,,I ! ii,,Li,..,L,,LL,L.iJ 11, iiiiiiLiiiii ' 1 ' W ' ill ' m Inchu 1>3 lU ' 1*6 ' VS VI 1'8 119 1 INCH 1 FOOT Y A 1,1,1,1,1,1,1, 1, J, I 1, 1, 1, nl,l,l,l,ln, I, ill, 1, 1,1,1,1,1, 1,1, 1,1, lJ.1.1, 1, 1,1,1,1, 1,1,1, 1, 1,1,1, 1,1,1,1,1^^ 1.1, 1,1, 1, 1,1,1, 1,1,1, 1,1,1,1,1,1,1,1, ill, 1,1,1, hi,!,!, I 1, 1,1.1,1,1,1,1, 1, 1,1, 1,1, 1,1,1,1,1 THE International System of Units— viated SI —is a modernized version 1 :ub c c ECI METER 1 LIQUID QUART system. It was established by inter also called (approximately) I liter 0.946 liter ment to provide a logical and interconnec ] 00c cm for all measurements in science, industry, SI is built upon a foundation of base units nitions, which appear on this chart. All oil The Six Base Units of Measured! METER-m SECOND s KILOGRAM -kg The meter is defined as 1 650 763.73 wavelengths in The second is defined as the duration of 9 192 631 The standard for the unit of mass, the kilogram, is a vacuum of the orange-red line of the spectrum of 770 cycles of the radiation associated with a specified cylinder of platinum-iridium alloy kept by the Inter- krypton-86. transition of the cesium atom. It is realized by tun- national Bureau of Weights and Measures at Paris. ing an oscillator to the resonance frequency of the A duplicate in the custody of the National Bureau of cesium atoms as they pass through a system of mag- Standards serves as the mass standard for the United nets and a resonant cavity into a detector. States. This is the only base unit still defined by an artifact. DIRECTION OF MAGNETIC FIELD U.S. PROTOTYPE An interferometer is used to measure length by means of light waves. Closely allied to the concept of mass is that of FROM OSCILLATOR force. The SI unit of force is the newton (N). A force of 1 newton, when applied for 1 second, will give to of atomic beam spectrometer. The trajectories A schematic an a 1 kilogram mass a speed of 1 meter per second are drawn for those atoms whose magnetic moments are The SI unit of area is the square meter (m ). Land (an acceleration of 1 meter per second per second). "flipped" in the transition region. is often measured by the hectare (10 000 square meters, or approximately 2.5 acres). The SI unit of volume is the cubic meter (m ). Fluid volume is often measured by the liter (0.001 cubic The number of periods or cycles per second is meter). called frequency. The SI unit for frequency is the —- ACCELERATION OF lm/j' 1968 hertz (Hz). One hertz equals one cycle per second. Standard frequencies and correct time are broad- Is 2 cast from NBS stations WWV, WWVB, WWVH, and One newton equals approximately two tenths of a WVWL, and stations of the U.S. Navy. pound of force. Many shortwave receivers pick up WWV on fre- The weight of an object is the force exerted on it quencies of 2.5, 5, 10, 15, 20, and 25 megahertz. by gravity. Gravity gives i mass l downward accelera- National Bureau of Standards Special Publication 304 A The standard radio broadcast band extends from tion of about 9.8m s (Supersedes Miscellaneous Publication 232) 535 to 1605 kilohertz. The SI unit for work and energy of any kind is For sale by the Superintendent of Documents, U.S. Government Dividing distance by time gives speed. The SI unit the joule (J). Printing Office, Washington, D.C. 20402 - Price 20 cents for speed is the meter per second (m/s), approxi- 1J — 1 N • lm mately 3 feet per second. References: The SI unit for power of any kird is the watt (W). Rate of change in speed is called acceleration. NBS Handbook 102, ASTM Metric Practice Guide, 40 cents The SI unit for acceleration is the meter per second NBS Misc. Publ. 247, Weights and Measures Standards of the iw= 4^ United States, A Brief History, 35 cents per second (m/s=). Is NBS Misc. Publ. 286. Units of Weight and Measure, Definitions and Tables of Equivalents, $1.50 Special Publication This chart is one-third the actual size of the full-scale wall chart, NBS 304, which is availabl m A ' U.S. DEPARTMENT OF COMMERCE ^mrmr^ The International System of Units (SI) National Bureau of Standards '<t 61 1 and its relationship to U.S. customary units 6,0 S „i„j ,, m l„i,,,l,i,Ii,!!i,,Jm„i ,,,,i j LL,LJi.a.i.iJ L±, lj lj l.l i ,.i SLlu i ,LuLa,, - l| l |l l| l |l l| ll|l|l l | | | | W^^ | « 1 1 1 1 1 1 1 1 1 1 1 1 3l4 1 3l5 1 zl« 2I3 214 m« 2l5 zk 2l7 2>S 219 3l0 3ll 3l2 3l3 D 2 FEET '''''''''''' llhlllllllllLlliJllllllllllllllllllllllllllllllll^ ially abbre- derived from these base units.
Load more

Recommended publications
  • The Metric System: America Measures Up. 1979 Edition. INSTITUTION Naval Education and Training Command, Washington, D.C
    DOCONENT RESUME ED 191 707 031 '926 AUTHOR Andersonv.Glen: Gallagher, Paul TITLE The Metric System: America Measures Up. 1979 Edition. INSTITUTION Naval Education and Training Command, Washington, D.C. REPORT NO NAVEDTRA,.475-01-00-79 PUB CATE 1 79 NOTE 101p. .AVAILABLE FROM Superintendent of Documents, U.S. Government Printing .Office, Washington, DC 2040Z (Stock Number 0507-LP-4.75-0010; No prise quoted). E'DES PRICE MF01/PC05 Plus Postage. DESCRIPTORS Cartoons; Decimal Fractions: Mathematical Concepts; *Mathematic Education: Mathem'atics Instruction,: Mathematics Materials; *Measurement; *Metric System; Postsecondary Education; *Resource Materials; *Science Education; Student Attitudes: *Textbooks; Visual Aids' ABSTRACT This training manual is designed to introduce and assist naval personnel it the conversion from theEnglish system of measurement to the metric system of measurement. The bcokteliswhat the "move to metrics" is all,about, and details why the changeto the metric system is necessary. Individual chaPtersare devoted to how the metric system will affect the average person, how the five basic units of the system work, and additional informationon technical applications of metric measurement. The publication alsocontains conversion tables, a glcssary of metric system terms,andguides proper usage in spelling, punctuation, and pronunciation, of the language of the metric, system. (MP) ************************************.******i**************************** * Reproductions supplied by EDRS are the best thatcan be made * * from
    [Show full text]
  • Metric System Units of Length
    Math 0300 METRIC SYSTEM UNITS OF LENGTH Þ To convert units of length in the metric system of measurement The basic unit of length in the metric system is the meter. All units of length in the metric system are derived from the meter. The prefix “centi-“means one hundredth. 1 centimeter=1 one-hundredth of a meter kilo- = 1000 1 kilometer (km) = 1000 meters (m) hecto- = 100 1 hectometer (hm) = 100 m deca- = 10 1 decameter (dam) = 10 m 1 meter (m) = 1 m deci- = 0.1 1 decimeter (dm) = 0.1 m centi- = 0.01 1 centimeter (cm) = 0.01 m milli- = 0.001 1 millimeter (mm) = 0.001 m Conversion between units of length in the metric system involves moving the decimal point to the right or to the left. Listing the units in order from largest to smallest will indicate how many places to move the decimal point and in which direction. Example 1: To convert 4200 cm to meters, write the units in order from largest to smallest. km hm dam m dm cm mm Converting cm to m requires moving 4 2 . 0 0 2 positions to the left. Move the decimal point the same number of places and in the same direction (to the left). So 4200 cm = 42.00 m A metric measurement involving two units is customarily written in terms of one unit. Convert the smaller unit to the larger unit and then add. Example 2: To convert 8 km 32 m to kilometers First convert 32 m to kilometers. km hm dam m dm cm mm Converting m to km requires moving 0 .
    [Show full text]
  • Varying Constants, Gravitation and Cosmology
    Varying constants, Gravitation and Cosmology Jean-Philippe Uzan Institut d’Astrophysique de Paris, UMR-7095 du CNRS, Universit´ePierre et Marie Curie, 98 bis bd Arago, 75014 Paris (France) and Department of Mathematics and Applied Mathematics, Cape Town University, Rondebosch 7701 (South Africa) and National Institute for Theoretical Physics (NITheP), Stellenbosch 7600 (South Africa). email: [email protected] http//www2.iap.fr/users/uzan/ September 29, 2010 Abstract Fundamental constants are a cornerstone of our physical laws. Any constant varying in space and/or time would reflect the existence of an almost massless field that couples to mat- ter. This will induce a violation of the universality of free fall. It is thus of utmost importance for our understanding of gravity and of the domain of validity of general relativity to test for their constancy. We thus detail the relations between the constants, the tests of the local posi- tion invariance and of the universality of free fall. We then review the main experimental and observational constraints that have been obtained from atomic clocks, the Oklo phenomenon, Solar system observations, meteorites dating, quasar absorption spectra, stellar physics, pul- sar timing, the cosmic microwave background and big bang nucleosynthesis. At each step we arXiv:1009.5514v1 [astro-ph.CO] 28 Sep 2010 describe the basics of each system, its dependence with respect to the constants, the known systematic effects and the most recent constraints that have been obtained. We then describe the main theoretical frameworks in which the low-energy constants may actually be varying and we focus on the unification mechanisms and the relations between the variation of differ- ent constants.
    [Show full text]
  • Geodesy Methods Over Time
    Geodesy methods over time GISC3325 - Lecture 4 Astronomic Latitude/Longitude • Given knowledge of the positions of an astronomic body e.g. Sun or Polaris and our time we can determine our location in terms of astronomic latitude and longitude. US Meridian Triangulation This map shows the first project undertaken by the founding Superintendent of the Survey of the Coast Ferdinand Hassler. Triangulation • Method of indirect measurement. • Angles measured at all nodes. • Scaled provided by one or more precisely measured base lines. • First attributed to Gemma Frisius in the 16th century in the Netherlands. Early surveying instruments Left is a Quadrant for angle measurements, below is how baseline lengths were measured. A non-spherical Earth • Willebrod Snell van Royen (Snellius) did the first triangulation project for the purpose of determining the radius of the earth from measurement of a meridian arc. • Snellius was also credited with the law of refraction and incidence in optics. • He also devised the solution of the resection problem. At point P observations are made to known points A, B and C. We solve for P. Jean Picard’s Meridian Arc • Measured meridian arc through Paris between Malvoisine and Amiens using triangulation network. • First to use a telescope with cross hairs as part of the quadrant. • Value obtained used by Newton to verify his law of gravitation. Ellipsoid Earth Model • On an expedition J.D. Cassini discovered that a one-second pendulum regulated at Paris needed to be shortened to regain a one-second oscillation. • Pendulum measurements are effected by gravity! Newton • Newton used measurements of Picard and Halley and the laws of gravitation to postulate a rotational ellipsoid as the equilibrium figure for a homogeneous, fluid, rotating Earth.
    [Show full text]
  • OF Versailles
    THE CHÂTEAU DE VErSAILLES PrESENTS science & CUrIOSITIES AT THE COUrT OF versailles AN EXHIBITION FrOM 26 OCTOBEr 2010 TO 27 FEBrUArY 2011 3 Science and Curiosities at the Court of Versailles CONTENTS IT HAPPENED AT VErSAILLES... 5 FOrEWOrD BY JEAN-JACqUES AILLAGON 7 FOrEWOrD BY BÉATrIX SAULE 9 PrESS rELEASE 11 PArT I 1 THE EXHIBITION - Floor plan 3 - Th e exhibition route by Béatrix Saule 5 - Th e exhibition’s design 21 - Multimedia in the exhibition 22 PArT II 1 ArOUND THE EXHIBITION - Online: an Internet site, and TV web, a teachers’ blog platform 3 - Publications 4 - Educational activities 10 - Symposium 12 PArT III 1 THE EXHIBITION’S PArTNErS - Sponsors 3 - Th e royal foundations’ institutional heirs 7 - Partners 14 APPENDICES 1 USEFUL INFOrMATION 3 ILLUSTrATIONS AND AUDIOVISUAL rESOUrCES 5 5 Science and Curiosities at the Court of Versailles IT HAPPENED AT VErSAILLES... DISSECTION OF AN Since then he has had a glass globe made that ELEPHANT WITH LOUIS XIV is moved by a big heated wheel warmed by holding IN ATTENDANCE the said globe in his hand... He performed several experiments, all of which were successful, before Th e dissection took place at Versailles in January conducting one in the big gallery here... it was 1681 aft er the death of an elephant from highly successful and very easy to feel... we held the Congo that the king of Portugal had given hands on the parquet fl oor, just having to make Louis XIV as a gift : “Th e Academy was ordered sure our clothes did not touch each other.” to dissect an elephant from the Versailles Mémoires du duc de Luynes Menagerie that had died; Mr.
    [Show full text]
  • The Beautiful Cubit System I Douglas 2019 the Beautiful Cubit System
    The Beautiful Cubit System I Douglas 2019 The Beautiful Cubit System Ian Douglas, B.Sc [email protected] 30 June 2019 Version 1.0.0 DOI: https://doi.org/10.5281/zenodo.3263864 This work is licensed under the Creative Commons Attribution 4.0 International License. Abstract An analysis of the Egyptian Royal cubit, presenting some research and opinions flowing from that research, into what I believe was the original cubit, and how it was corrupted. I show various close arithmetic approximations and multiple ways of getting the divisions of the cubit, as well as some related measures. The cubit also encapsulates the basic components for the metric system. Keywords: Egyptology, metrology, royal cubit, cubit, metre, foot, metric system Contents 1. Introduction 2. Overview of current understanding 3. An alternative origin 4. Different ways of approximating the royal cubit 5. Different ways of getting the cubit divisions 6. Geometry, the Royal Cubit and the metric system 7. Bibliography 1. Introduction The cubit is a well-know ancient measure of length, used around various places in the Middle East and Mediterranean region in the distant past. 1 The Beautiful Cubit System I Douglas 2019 It is allegedly based on the length of a human (male) fore-arm. It is typically measured from the back of the elbow to some point between the wrist and the end of the outstretched middle finger, or in some variants, a point beyond that. The problem with this approach is that everyone’s arm is a different length. If the heights of the dynastic Egyptians is taken as representative, then their arms would have been too short to justify the accepted lengths.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • How Are Units of Measurement Related to One Another?
    UNIT 1 Measurement How are Units of Measurement Related to One Another? I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind... Lord Kelvin (1824-1907), developer of the absolute scale of temperature measurement Engage: Is Your Locker Big Enough for Your Lunch and Your Galoshes? A. Construct a list of ten units of measurement. Explain the numeric relationship among any three of the ten units you have listed. Before Studying this Unit After Studying this Unit Unit 1 Page 1 Copyright © 2012 Montana Partners This project was largely funded by an ESEA, Title II Part B Mathematics and Science Partnership grant through the Montana Office of Public Instruction. High School Chemistry: An Inquiry Approach 1. Use the measuring instrument provided to you by your teacher to measure your locker (or other rectangular three-dimensional object, if assigned) in meters. Table 1: Locker Measurements Measurement (in meters) Uncertainty in Measurement (in meters) Width Height Depth (optional) Area of Locker Door or Volume of Locker Show Your Work! Pool class data as instructed by your teacher. Table 2: Class Data Group 1 Group 2 Group 3 Group 4 Group 5 Group 6 Width Height Depth Area of Locker Door or Volume of Locker Unit 1 Page 2 Copyright © 2012 Montana Partners This project was largely funded by an ESEA, Title II Part B Mathematics and Science Partnership grant through the Montana Office of Public Instruction.
    [Show full text]
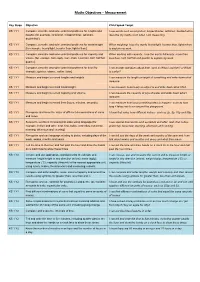
  • Maths Objectives – Measurement
    Maths Objectives – Measurement Key Stage Objective Child Speak Target KS 1 Y1 Compare, describe and solve practical problems for lengths and I use words such as long/short, longer/shorter, tall/short, double/half to heights [for example, long/short, longer/shorter, tall/short, describe my maths work when I am measuring. double/half]. KS 1 Y1 Compare, describe and solve practical problems for mass/weight When weighing, I use the words heavy/light, heavier than, lighter than [for example, heavy/light, heavier than, lighter than]. to explain my work. KS 1 Y1 Compare, describe and solve practical problems for capacity and When working with capacity, I use the words full/empty, more than, volume [for example, full/empty, more than, less than, half, half full, less than, half, half full and quarter to explain my work. quarter]. KS 1 Y1 Compare, describe and solve practical problems for time [for I can answer questions about time, such as Who is quicker? or What example, quicker, slower, earlier, later]. is earlier? KS 1 Y1 Measure and begin to record lengths and heights. I can measure the length or height of something and write down what measure. KS 1 Y1 Measure and begin to record mass/weight. I can measure how heavy an object is and write down what I find. KS 1 Y1 Measure and begin to record capacity and volume. I can measure the capacity of jugs of water and write down what I measure. KS 1 Y1 Measure and begin to record time (hours, minutes, seconds). I can measure how long something takes to happen - such as how long it takes me to run around the playground.
    [Show full text]
  • U.S. Metric Study Interim Report
    U.S. METRIC STUDY INTERIM REPORT THE CONSUMER imHHMHPHr U.S. METRIC SUBSTUDY REPORTS The results of substudies of the U.S. Metric Study, while being evaluated for the preparation of a comprehensive report to the Congress, are being published in the interim as a series of NBS Special Publications. The titles of the individual reports are listed below. REPORTS ON SUBSTUDIES NBS SP345-I: International Standards (issued December 1970, SD Catalog No. CI 3. 10:345-1, Price $1.25) NBS SP345-2: Federal Government: Civilian Agencies (issued July 1971, SD Catalog No. CI 3. 10:345-2, price $2.25) NBS SP345-3: Commercial Weights and Measures (issued July 1971, SD Catalog No. CI 3. 10:345-3, price $1.00) NBS SP345-4: The Manufacturing Industry (issued July 1971, SD Catalog No. C 1 3. 10:345-4, price $ 1 .25) NBS SP345-5 Nonmanufacturing Businesses (in press) NBS SP345-6 Education (in press) NBS SP345-7 The Consumer (this publication) NBS SP345-8 International Trade (in press) NBS SP345-9 Department of Defense (issued July 1971, SD Catalog No. C 1 3. 1 0:345-9, price $ 1 .25) NBS SP345-10: A History of the Metric System Controversy in the United States (in press) NBSSP345-11: Engineering Standards (issued July 1971, SD Catalog No. C 1 3. 1 0:345-1 1 , price $2.00) NBSSP345-12: Testimony of Nationally Representative Groups (issued July 1971, SD Catalog No. C13. 10:345-12, price $1.50) COMPREHENSIVE REPORT ON THE U.S. METRIC STUDY NBS SP345: To be published in August 1971 Those publications with catalog numbers have already been issued, and may be purchased from the Superintendent of Documents, Government Printing Office, Washington, D.C.
    [Show full text]
  • Yd.) 36 Inches = 1 Yard (Yd.) 5,280 Feet = 1 Mile (Mi.) 1,760 Yards = 1 Mile (Mi.)
    Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com Units of length 12 inches (in.) = 1 foot (ft.) 3 feet = 1 yard (yd.) 36 inches = 1 yard (yd.) 5,280 feet = 1 mile (mi.) 1,760 yards = 1 mile (mi.) ©www.thecurriculumcorner.com 1. Find the greatest length. 2. Find the greatest length. 9 in. or 1 ft. 3 ft. or 39 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 3. Find the greatest length. 4. Find the greatest length. 1 ft. 7 in. or 18 in. 4 ft. 4 in. or 55 in. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 5. Find the greatest length. 6. Find the greatest length. 1 ft. 9 in. or 2 ft. 7 ft. or 2 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 7. Find the greatest length. 8. Find the greatest length. 26 in. or 2 ft. 6 yd. or 17 ft. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 9. Find the greatest length. 10. Find the greatest length. 5 ft. or 1 ½ yd. 112 in. or 3 yd. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 11. Find the greatest length. 12. Find the greatest length. 99 in. or 3 yd. 11,000 ft. or 2 mi. ©www.thecurriculumcorner.com ©www.thecurriculumcorner.com 13.
    [Show full text]
  • Snow Science Fact Sheet
    BASIC FORMULAS 1. Typical Material Cost Breakdown of a Snowmaking System 2. Snowmaking Technology Energy Use Comparison 3. Typical Air Compressor Discharge Temperature 4. Calculating Friction Loss of Water in Pipe-lines 5. Calculating Air Pressure Loss Due to Friction 6. Calculating Horsepower For Water Pump 7. Calculating Operating Cost 8. Water Snow Relationships 3.2 Gallons = 1 FT³ of Snow 1 Gallon = 8.342 lbs 1 FT³ Water = 7.48 Gallons 1 Acre = 43,560 FT² 1 Acre Foot of Snow = 180,000 Gallons of Water 9. English to Metric Conversion Factors English Units Multiply By Metric Units Gallons (GAL.) 3.785 Litres (L) Gallons Per Minute (GPM) 3.785 Litres Per Minute (LPM) Gallons Per Minute (GPM) 0.0631 Litres Per Second (LPS) Acres 0.40469 Hectares Acres 4046.9 Meters² Feet 0.3048 Meters Cubic Feet (FT³) 0.0283 Cubic Meters (M 3) Horsepower (HP) 0.7457 Kilowatts Pounds Per Square Inch (PSI) 6.895 Kilopascals (KPA) Gal/Min 0.2271 M³/HR Hectare-M 10,000 M³ 10. How to Determine Snow Quality One could collect fresh snow samples and determine weight per Cubic Foot or Cubic Meter and state the quality in density like pounds per Cubic Foot or density per Cubic Meter. A far simpler and practical method is to test the snow on the ground in the production plume while snow guns are operating by doing a Snow Ball Test. The quality can be determined on a scale from 1 to 6 according to the table below: The Snowball Test Snow Quality Description 1 Snow cannot be packed, powder 2 Snow can only be packed into a loose ball that falls apart 3 Snow can be packed into a ball that can be broken apart 4 Snow can be packed into a dense ball that does not change color when squeezed 5 Snow can be packed into a dense ball that changes to a darker color when squeezed but little or no water comes out 6 Snow can be packed into a dense ball that discharges water when squeezed .
    [Show full text]