DOCSLIB.ORG

University of Education, Lahore

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
University of Education, Lahore DEVELOPMENT OF MATH PROFICIENCY TEST USING ITEM RESPONSE THEORY (IRT) MUHAMMAD AZEEM Reg. No. 0499086 DIVISION OF EDUCATION UNIVERSITY OF EDUCATION, LAHORE 2012 DEVELOPMENT OF MATH PROFICIENCY TEST USING ITEM RESPONSE THEORY (IRT) MUHAMMAD AZEEM Reg. No. 0499086 Submitted in partial fulfillment of the requirement for the degree of Doctor of Philosophy in Education at Division of Education, University of Education, Lahore 2012 ii IN THE NAME OF ALLAH, WHO IS MOST MERCIFUL AND BENEFICENT iii This Work is dedicated to: MUHAMMAD (PEACE BE UPON HIM) iv PhD Thesis Certificate of Acceptance Name of Student Student No. Programme Muhammad Azeem 04-PhD-001 PhD (Education) TOPIC: DEVELOPMENT OF MATH PROFICIENCY TEST BASED ON ITEM RESPONSE THEORY (IRT) AT SECONDARY LEVEL Date of Acceptance: ___________________ THESIS COMMITTEE SR. # Name Position Signature 1. 2. 3. 4. 5. v ACNOWLEDGEMENTS Firstly, I owe to the almighty ALLAH, The Most Merciful and The Most Beneficent, who give me courage to accomplish this research work. The PhD scholar is deeply indebted to Dr. Muhammad Bashir Gondal, supervisor of this doctoral research work, for his affection, guidance, interest, encouragement and supportive attitude, and constructive advice which enlightened my ways in completion of my research project. Besides it, researcher is also indebted to him for providing necessary facilities and feedback during this research project that helped me a lot in accomplishment of my research project. Special bundle of thanks go to Dr Izhar-ul-Haq (Late) for encouragement and supportive attitude, and constructive advice for completion of my doctoral research at University of Education. May ALLAH rest his soul in paradise (Ameen). Special bundle of thanks go to Dr. Muhammad Khalid Mehmood, Assisstant professor, University of Education, Lahore, for his encouragement and supportive attitude for data analysis by using IRT software. Thanks go to Dr. Glenn Fulcher, Dr Chris Comber, Dr Janet Ainley, and Dr Saeeda Shah, faculty members of School of Education, University of Leicester, UK for their encouragement and help in research work. Thanks go to all other faculty members especially Dr Muhammad Khalid Ibrahim and Dr Shahbaz Khan of Division of Education, University of Education, Lahore, for their helping and supportive attitude. Thanks go to Dr Muhammad Saeed, Madam Bushra and Muhammad Tanveer Iqbal professionals working in PITE, Lahore for their help in Item development and test construction. Thanks go to Ch. Munir Ahmed, principal, GHSS Chak Jhumra, for granting study leave and supporting in this research work. Thanks go to Muhammad Tanveer Afzal, PhD Scholar, UE, Lahore, Muhammad Idrees Asad, PhD Scholar, UE, Lahore, Naseer Ahmad, PhD Scholar, UE, Lahore, Khalil-ur-Rehman, PhD Scholar, UE, Lahore, Noor Muhammad Asif, PhD Scholar, UE, Lahore for their help in construction & validation of math proficiency test and data collection. Thanks go to all prospective teachers of Division of Education, University of Education, Lahore, and all teacher educators (T.E.) working in all district of PUNJAB province especially Saadia Hadiat, Sahiwal, Nasrullah Bhatti, Bhakkar, Amjad Mahmood, Attock, Asmat Ullah, DG Khan, Muhammad Ishfaq Ahmad, Sargodha, Muhammad Akram Junaid, Lodhran, Muhammad Arshad Javid, Bahawalnagar, Malik Muhammad Ahmed, Bahawalpur, Mr Amjad Ali Bhatti, Hafizabad, for their sincere, honest, and swift participation as test administrators. Special thanks go to Syed Afaq Assisstant professor Math, divisional educational technology resource centre, Madam Shafia Assisstant Professor Math, federal college of education, Islamabad, Qasimabad, Karachi, Shabana Haider Assisstant professor Math, Govt. Elementry College, Hussainabad, Karachi, Irfan Ullah Quraishi Assisstant professor Math, Govt. F.B. area Karachi, Nadeem Sultan SSS Math PEACE, NWFP, Naveed Alam Math teacher, Leicester Islamic Academy, UK, Thanks go to Muhammad Nusrullah, Assistant Education Officer, Chishtian, Munir Hussain PhD Scholar, IER, PU, Lahore, Shafqat Hussain SSS statistics, GCET, vi Mianwali, Muhammad Akram SS economics, GHSS Jalalpur Pirwala, Multan, Rai Manzoor Ahmad, SSS biology GCET Muzaffargarh, Zulfiqar Ali, Executive District Officer EDO, Nankana Sahib, Bakar Hussain Tariq SST, GHS 203RB Faisalabad, Imran Ashraf SST, GHS 493 JB, Jhang, Omer Draz, SSS Math GHSS Lalian, Muhammad Ajmal Headmaster Govt. Model H/S Khanewal, Munir Ahmad, Senior Headmaster GHS 202RB Faisalabad, Rasid Ahmad Khawer SST, GHS Pakpatan, Muhammad Khalid SST, GHS Salarwala, Faisalabad, Nadeem AT, GES 190RB Faisalabad, Muhammad Afzal HM, GHS Dijkot, Faisalabad, Bakar Hussain Tariq SST GHS Manawala, Faisalabad, for their sincere, honest, and swift participation as test administrators. Thanks go to Abdul Ghaffar, SST, GHSS Chak Jhumra, Zulfiqar Ali, SV, GHSS Chak Jhumra, Amjad Naseem Ansari DTE, GHS Salarwala for their sincere, honest, and swift participation as test administrators and translation of English version of Math Proficiency Test in to Urdu version. Thanks go to David J. Weiss, Professor of Psychology at Applied Psychological Measurement Inc. member of APM Graduate Student Grants committee, N660 Elliott Hall, University of Minnesota Minneapolis MN 55455-0344, U.S.A. for providing IRT Software Multilog 7 and IRT related books. Thanks go to Susan Cooper Loomis, Assistant Director, Psychometrics, National Assessment Governing Board, USA, for granting permission to adapt NAEP’s Math assessment framework in this research study. Special thanks go to higher education commission HEC of Pakistan for providing funds for doctoral fellowship at Division of Education, University of Education, Lahore and funds for foreign visit of School of Education, University of Leicester, UK, under International Research Support Initiatives Program IRSIP to complete this thesis. Thanks go to Shah Nawaz IT specialist of PEAS for his support in editing and designing thesis. Thanks go to all those who helped me in my research work but I have forgot because of deeply engagement with research activities. Special thanks go to all my family members for suffering a lot of due to my busyness and friends for supporting in this research work. Muhammad Azeem vii DEVELOPMENT OF MATH PROFICIENCY TEST USING ITEM RESPONSE THEORY (IRT) ABSTRACT This study was conducted to develop a math proficiency test using IRT, based on NAEP’s adapted Mathematics Framework, and aligned with the newly developed standards, and benchmarks of National Mathematics Curriculum. Mathematical Proficiency is the ability to use the mathematical power for conceptual understanding, procedural knowledge, and problem-solving in the real world using appropriate strategies. One hundred and ninety six multiple choice and short constructed response items were developed. Due to limitations of the study only, multiple choice and short constructed response, dichotomously scored items were developed. Items were spot tested on 200 students and piloted on 550 students. A final 60-item math proficiency test was constructed. Stratified cluster sampling technique was used for administration of final math proficiency test. All the 9th grade students studying in public high and higher secondary schools in the province of Punjab comprised the population of the study. Sample of 2680 students and 134 schools was selected using sample design tables and IRT based analysis requirements. Final math proficiency test was administered and data was received from 2617 students. Data was analyzed by using SPSS, Conquest, and Multilog software. Data was well fitted with Rasch Model. The infit and outfit means square statistics of items was within 0.8 to 1.30. The reliability and discrimination index of final math proficiency test was above 0.90 and 0.45 respectively. The IRT based person-item map showed that test items covered ±3 range of abilities. Test characteristics and item characteristics curves, factor analysis, and dimensionality analysis also supported the reliably and validity of the test. Different viii estimations-WLE, EAP, and MLE also supported reliability and validity of test items. Estimations WLE, EAP, and MLE have advantages and disadvantages over each other. For this study the average of these estimations was used as proficiency score for each student. It explored that math proficiency test is appropriately constructed. Replication of this study is recommended by using 2PLM and 3PLM of Item Response Theory (IRT). ix DECLARATION I, Muhammad Azeem S/O Muhammad Yaqub Registration No. 0499086, a student of PhD at the University of Education, do hereby solemnly declare that the thesis entitled “Development of Math Proficiency Test Using Item Response Theory (IRT)” submitted by me in partial fulfillment of PhD degree (Education) is my original work, except where otherwise acknowledge in the text, and has not been submitted or published earlier and shall not, in future, be submitted by me for obtaining any degree from this or any other University or institution. Signature_______________________ Muhammad Azeem x TABLE OF CONTENTS Sr. No. Contents Page No. i Title i, ii ii In the name of Allah, Who is most merciful and beneficent iii iii Dedication to Muhammad (P.B.U.H) iv iv Approval Sheet v v Acknowledgments vi vi Abstract viii vii Declaration x viii Table of Contents xi viii List of Appendices xviii ix List of Tables xix x List of Figures xxi xi Acronyms xxiii CHAPTER NO. 1 : INTRODUCTION 1.1 Introduction 1 1.2 Statement of Problem 4 1.3 Significance of the study 5 1.4 Objectives of Study 7 1.5
Load more

Recommended publications
  • *Free Courses* *Learn How You Can Earn Online* Apply Now! ADMISSIONS ARE OPEN for BOTH ONLINE and ON-CAMPUS CLASSES!
    *Free Courses* *Learn how you can earn online* www.erozgaar.pitb.gov.pk/apply Apply Now! ADMISSIONS ARE OPEN FOR BOTH ONLINE AND ON-CAMPUS CLASSES! Courses we are offering: 1- Technical 2- Creative Design 3- Content Marketing and Advertising 4- E-Commerce Freelancing Course is taught along with all the above-mentioned courses so the trainees can learn to monetize their skills. Applications are LIVE for e-Rozgaar centers at the following institutes: 1- University of Sargodha, Sargodha 2- University of Gujrat, Gujrat 3- University of the Punjab, Lahore 4- University of Engineering and Technology, Lahore 5- University of Education, Vehari 6- Government College Women University, Faisalabad 7- University of Agriculture, Faisalabad 8- Lahore College for Women University, Lahore 9- University of Education, Jauharabad Khushab 10- University of Mianwali 11- COMSATS University Islamabad, Sahiwal Campus 12- University of the Punjab, Jhelum Campus 13- University of the Punjab, Gujranwala Campus 14- COMSATS University Islamabad, Wah Campus 15- Rawalpindi Women University, Rawalpindi 16- Government College Women University, Sialkot 17- COMSATS University Islamabad, Attock Campus 18- Bahauddin Zakariya University, Multan 19- NFC Institute of Engineering and Technology, Multan 20- University of Sargodha, Sub Campus Bhakkar 21- Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan 22- Bahauddin Zakariya University, Sub Campus Bahadur, Layyah 23- Bahauddin Zakariya University, Sub Campus Lodhran 24- Ghazi University, Dera Ghazi
    [Show full text]
  • University of Education
    University of Education Terms of Reference “Enlistment of Contractors Rules 2019” For Works Costing Up to Rs. 100 million University of Education, Lahore. Name of Work “Enlistment of Contractors Rules 2019” For Works Costing Up to Rs. 100 million Dead line of issuance of tender 25 June, 2019 up to 4:00 PM Date for Submission of Tender 27 June, 2019 up to 12:00 PM Issued to Issued by Signature: _______________________________ Date: ___________________________________ Office Stamp Note: The officer opening the tender shall reject the tender which does not bear the stamp and signature of the issuing official and which is not submitted by the same contractor to whom the tender form was issued. Contractor Engineer Part 1 Title, Commencement and Its Application 1.1 The Rules may be called the University of Education “Enlistment of Contractors Rules 2018” 1.2 They shall come into force at once. These Rules shall apply to make Enlistment/ Renewal of contractors for categories mentioned here under for execution of M&R/ Original works of University of Education and in all its Campuses:- i. CE-09 Sewerage/ water supply works. ii. CE-10 General civil Engineering works etc. iii. EE-02 Security, safety surveillance system. iv. EE-03 Building automation system & Energy generation system. v. EE-04 Low voltage installation. vi. EE-06 Specialized lightening system. Any other category as deemed by Competent Authority. 1.3 Location of Campuses . University of Education, College Road Township, Lahore. University of Education, Lower Mall Campus, Lahore. University of Education, Bank Road Campus, Lahore. University of Education, Samnabad Road Campus Faisalabad.
    [Show full text]
  • Résumé Qudsia Kalsoom, Phd HEC-Approved Phd Supervisor
    Résumé Qudsia Kalsoom, PhD HEC-Approved PhD Supervisor Department of Educational Leadership & Management Beaconhouse National University Email: [email protected] Academic Qualifications Qualification University/ Board Year CGPA PhD Education Lahore College for Women 2017 Coursework University, Pakistan CGPA = 3.96/4 Thesis Title: Thesis Evaluated by Prof Dr ESD Literacy-Based Model for Michele Biasutti (University of Preservice Elementary Teachers: A Focus on Critical & Environmental Padova, Italy), Prof Dr Anders Consciousness and Effective Breidlid (University of Oslo, Teacher Development Norway), Prof Dr Nasir Mahmood (Allama Iqbal Open University) and http://prr.hec.gov.pk/jspui/handle Prof Dr Zafar Iqabal (UMT) /123456789/9569 MPhil Education University of Education, Pakistan 2014 CGPA = 3.96/4 Masters in Educational Leadership University of Management & 2011 CGPA = 3.95/4 & Management Technology, Pakistan M.Sc. Chemistry Punjab University, Pakistan 1998 1st Division B.Sc. (Major: Chemistry, Botany, Punjab University, Pakistan 1995 Upper 2nd Zoology) Division F.Sc. (Major: Chemistry, Physics, Lahore Board, Pakistan 1993 1st Division Biology) Matriculation (Major: Chemistry, Lahore Board, Pakistan 1990 1st Division Physics, Biology, Mathematics) Professional Qualifications & Trainings 2002 Completed Certificate (6 months) in Professional Studies in Education from Bradford University, UK. 2004 Completed a Certificate “Child Friendly Schools: Theory & Practice” organized by Ministry of Education Thailand and UNICEF, Thailand. 2008 Completed Advanced Postgraduate Diploma (1 year) in Teachers Professional Development from Ali Institute of Education, Lahore, Pakistan. 1 2017 Participated in an e-Seminar (from May 29 to June 2, 2017) on “Transforming Teacher Education to Improve Learning Outcomes”. The seminar was organized by International Institute of Educational Planning, UNESCO.
    [Show full text]
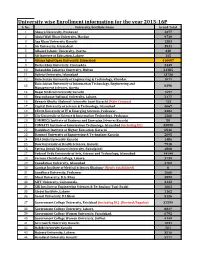
  • University Wise Enrollment Information for the Year 2015-16P S
    University wise Enrollment information for the year 2015-16P S. No. University/Institute Name Grand Total 1 Abasyn University, Peshawar 4377 2 Abdul Wali Khan University, Mardan 9739 3 Aga Khan University Karachi 1383 4 Air University, Islamabad 3531 5 Alhamd Islamic University, Quetta. 338 6 Ali Institute of Education, Lahore 115 8 Allama Iqbal Open University, Islamabad 416607 9 Bacha Khan University, Charsadda 2449 10 Bahauddin Zakariya University, Multan 21385 11 Bahria University, Islamabad 13736 12 Balochistan University of Engineering & Technology, Khuzdar 1071 Balochistan University of Information Technology, Engineering and 13 8398 Management Sciences, Quetta 14 Baqai Medical University Karachi 1597 15 Beaconhouse National University, Lahore. 2177 16 Benazir Bhutto Shaheed University Lyari Karachi (Main Campus) 753 17 Capital University of Science & Technology, Islamabad 4067 18 CECOS University of IT & Emerging Sciences, Peshawar. 3382 19 City University of Science & Information Technology, Peshawar 1266 20 COMMECS Institute of Business and Emerging Sciences Karachi 50 21 COMSATS Institute of Information Technology, Islamabad (including DL) 35890 22 Dadabhoy Institute of Higher Education, Karachi 6546 23 Dawood University of Engineering & Technology Karachi 2095 24 DHA Suffa University Karachi 1486 25 Dow University of Health Sciences, Karachi 7918 26 Fatima Jinnah Women University, Rawalpindi 4808 27 Federal Urdu University of Arts, Science and Technology, Islamabad 14144 28 Forman Christian College, Lahore. 3739 29 Foundation University, Islamabad 4702 30 Gambat Institute of Medical Sciences Khairpur (Newly established) 0 31 Gandhara University, Peshawar 1068 32 Ghazi University, D.G. Khan 2899 33 GIFT University, Gujranwala. 2132 34 GIK Institute of Engineering Sciences & Technology Topi-Swabi 1661 35 Global Institute, Lahore 1162 36 Gomal University, D.I.Khan 5126 37 Government College University, Faislabad (including DL) (Revised/Regular) 32559 38 Government College University, Lahore.
    [Show full text]
  • Unai Members List August 2021
    UNAI MEMBER LIST Updated 27 August 2021 COUNTRY NAME OF SCHOOL REGION Afghanistan Kateb University Asia and the Pacific Afghanistan Spinghar University Asia and the Pacific Albania Academy of Arts Europe and CIS Albania Epoka University Europe and CIS Albania Polytechnic University of Tirana Europe and CIS Algeria Centre Universitaire d'El Tarf Arab States Algeria Université 8 Mai 1945 Guelma Arab States Algeria Université Ferhat Abbas Arab States Algeria University of Mohamed Boudiaf M’Sila Arab States Antigua and Barbuda American University of Antigua College of Medicine Americas Argentina Facultad de Ciencias Económicas de la Universidad de Buenos Aires Americas Argentina Facultad Regional Buenos Aires Americas Argentina Universidad Abierta Interamericana Americas Argentina Universidad Argentina de la Empresa Americas Argentina Universidad Católica de Salta Americas Argentina Universidad de Congreso Americas Argentina Universidad de La Punta Americas Argentina Universidad del CEMA Americas Argentina Universidad del Salvador Americas Argentina Universidad Nacional de Avellaneda Americas Argentina Universidad Nacional de Cordoba Americas Argentina Universidad Nacional de Cuyo Americas Argentina Universidad Nacional de Jujuy Americas Argentina Universidad Nacional de la Pampa Americas Argentina Universidad Nacional de Mar del Plata Americas Argentina Universidad Nacional de Quilmes Americas Argentina Universidad Nacional de Rosario Americas Argentina Universidad Nacional de Santiago del Estero Americas Argentina Universidad Nacional de
    [Show full text]
  • Identification of the Educational Problems at Higher Secondary
    Review of Education, Administration and Law (REAL) Vol. 3, (3) 2020, 403-410 Identification of the Educational Problems at Higher Secondary Schools of Lahore a b c d Raheela Sarfraz, Sadaf Jabeen, Muhammad Ashraf Sajid, Muhammad Shahid Zulfiqar Ali a Minhaj University Lahore, Pakistan Email: [email protected] b Assistant Professor, Lahore College for Women University , Lahore , Pakistan Email: [email protected] c PhD Scholar, University of Education, Lahore, Pakistan Email: [email protected] d PhD Scholar, University of Education, Lahore, Pakistan Email: [email protected] ARTICLE DETAILS ABSTRACT History: This study was conducted with the aim to find out educational problems Accepted 27 Nov 2020 faced by the teachers at higher secondary level by keeping in mind their Available Online 31 Dec 2020 most common issues regarding discipline, books, environment regarding teaching and learning, conduction of exams. This study was descriptive Keywords: in nature and survey method was used to identify the higher secondary Education, Problems, Higher teachers’ perceptions about educational problems that they faced. The Secondary Schools, Teachers’ sample has been selected while using the convenient sampling technique. Perceptions The total 215 teachers were working in the boys’ HSCs selected as the sample. On the other hand 282 female teachers have been selected for the JEL Classification: study as a sample. The researcher collected the data while adapting the P36, F37, F39 close ended questionnaire developed by (Ayub, 2014). There are 32 items included in the aforementioned research questionnaire. The descriptive statistics percentage and Mann Whitney U test was applied by the DOI: 10.47067/real.v3i3.85 researcher to analyze the data.
    [Show full text]
  • Curriculum Vitae Qudsia Kalsoom Assistant Professor School of Education Beaconhouse National University Email: [email protected]
    Curriculum Vitae Qudsia Kalsoom Assistant Professor School of Education Beaconhouse National University Email: [email protected] Academic Qualifications Qualification University/ Board Year Division/ CGPA PhD Education Lahore College for Women 2017 Coursework University, Pakistan CGPA = 3.96 MPhil Education University of Education, 2014 CGPA = 3.96/4 Pakistan Masters in Educational University of Management & 2011 CGPA = 3.95/4 Leadership & Management Technology, Pakistan M.Sc. Chemistry Punjab University 1998 First Division B.Sc. (Major: Chemistry, Punjab University 1995 Upper 2nd Botany, Zoology) Division F.Sc. (Pre-medical) Lahore Board 1993 1st Division Matriculation Lahore Board 1990 1st Division Professional Qualifications & Trainings Participated in an e-Seminar (from May 29 to June 2, 2017) on “Transforming Teacher Education to Improve Learning Outcomes”. The seminar was organized by International Institute of Educational Planning, UNESCO. Completed Advanced Postgraduate Diploma in Teachers Professional Development in 2008 from Ali Institute of Education, Lahore. Completed Certificate in Professional Studies in Education in 2002 from Bradford University. Completed a Certificate in Child Friendly Schools: Theory & Practice organized by Ministry of Education Thailand and UNICEF in 2004. Research Publications in Refereed/ Impact Factor Journals Kalsoom, Q. & Khanam, A. (2017). Inquiry into Sustainability Issues by Preservice Teachers: A Pedagogy to Enhance Sustainability Consciousness. Journal of Cleaner Production. Volume 164, pp. 1301-1311. https://doi.org/10.1016/j.jclepro.2017.07.047 (Journal Impact Factor = 1.46) Kalsoom, Q., Khanam, A. & Quraishi, U. (2017). Sustainability Consciousness of the Presevice Teachers in Pakistan. International Journal of Sustainability in Higher Education. https://doi.org/10.1108/IJSHE-11-2016-0218.
    [Show full text]
  • College Codes (Outside the United States)
    COLLEGE CODES (OUTSIDE THE UNITED STATES) ACT CODE COLLEGE NAME COUNTRY 7143 ARGENTINA UNIV OF MANAGEMENT ARGENTINA 7139 NATIONAL UNIVERSITY OF ENTRE RIOS ARGENTINA 6694 NATIONAL UNIVERSITY OF TUCUMAN ARGENTINA 7205 TECHNICAL INST OF BUENOS AIRES ARGENTINA 6673 UNIVERSIDAD DE BELGRANO ARGENTINA 6000 BALLARAT COLLEGE OF ADVANCED EDUCATION AUSTRALIA 7271 BOND UNIVERSITY AUSTRALIA 7122 CENTRAL QUEENSLAND UNIVERSITY AUSTRALIA 7334 CHARLES STURT UNIVERSITY AUSTRALIA 6610 CURTIN UNIVERSITY EXCHANGE PROG AUSTRALIA 6600 CURTIN UNIVERSITY OF TECHNOLOGY AUSTRALIA 7038 DEAKIN UNIVERSITY AUSTRALIA 6863 EDITH COWAN UNIVERSITY AUSTRALIA 7090 GRIFFITH UNIVERSITY AUSTRALIA 6901 LA TROBE UNIVERSITY AUSTRALIA 6001 MACQUARIE UNIVERSITY AUSTRALIA 6497 MELBOURNE COLLEGE OF ADV EDUCATION AUSTRALIA 6832 MONASH UNIVERSITY AUSTRALIA 7281 PERTH INST OF BUSINESS & TECH AUSTRALIA 6002 QUEENSLAND INSTITUTE OF TECH AUSTRALIA 6341 ROYAL MELBOURNE INST TECH EXCHANGE PROG AUSTRALIA 6537 ROYAL MELBOURNE INSTITUTE OF TECHNOLOGY AUSTRALIA 6671 SWINBURNE INSTITUTE OF TECH AUSTRALIA 7296 THE UNIVERSITY OF MELBOURNE AUSTRALIA 7317 UNIV OF MELBOURNE EXCHANGE PROGRAM AUSTRALIA 7287 UNIV OF NEW SO WALES EXCHG PROG AUSTRALIA 6737 UNIV OF QUEENSLAND EXCHANGE PROGRAM AUSTRALIA 6756 UNIV OF SYDNEY EXCHANGE PROGRAM AUSTRALIA 7289 UNIV OF WESTERN AUSTRALIA EXCHG PRO AUSTRALIA 7332 UNIVERSITY OF ADELAIDE AUSTRALIA 7142 UNIVERSITY OF CANBERRA AUSTRALIA 7027 UNIVERSITY OF NEW SOUTH WALES AUSTRALIA 7276 UNIVERSITY OF NEWCASTLE AUSTRALIA 6331 UNIVERSITY OF QUEENSLAND AUSTRALIA 7265 UNIVERSITY
    [Show full text]
  • Intermediate Admission Handbook
    www.kinnaird.edu.pk 93-Jail Road, Lahore. INTERMEDIATE Tel: 92 42 99203781-4 Fax: 92 42 99203788 ADMISSION HANDBOOK 2020-21 Vision Table and of Contents Mission 02 Academic Calendar 32 Sports Vision Statement The vision for Kinnaird is be a Centre of Excellence for the education of women in South Asia, by offering an academic 04 Message from the Principal 34 Addmision In The International Program programVision Statement of International Standards, engaging in research and service that serves the development of new knowledge and Theideas vision and promotesfor Kinnaird social is be responsibility a Centre of andexcellence active citizenship. for the education This is ofin womenrecognition in South and continuation Asia, by offering of the an reputation academic 06 Welcome to Kinnaird 44 Fee Structure programthe college of hasInternational of being the Standards, most prominent engaging and in researchprestigious and institution service that for serveswomen the in Pakistan.development of new knowledge and ideas and promotes social responsibility and active citizenship. This is in recognition and continuation of the reputation the 08 Campus Facilities 56 Academic Rules and Regulations college has of being the most prominent and prestigious institution for women in Pakistan. 10 Library 60 Student Code of Conduct 12 Accommodation 62 Teaching Faculty 72 Administration Mission Statement 14 Cafe The Mission of Kinnaird is to provide access to an education that is holistic, of quality and relevant to the context and Vision Statement 15 Extra Curricular
    [Show full text]
  • Education System of Pakistan and the UK: Comparisons in Context to Inter-Provincial and Inter-Countries Reflections
    Bulletin of Education & Research December 2007, Vol. 29, No. 2, pp. 43-57 Education System of Pakistan and the UK: Comparisons in Context to Inter-provincial and Inter-countries Reflections Muhammad Saeed* Abstract This paper addresses the comparisons of the education system of Pakistan and the UK from six dimensions i.e. education and training authority, educational structure, curriculum formulation, assessment and evaluation, supervision and management, and teacher education and training. The results revealed that against all these six dimensions, similarities and differences exist within four provinces of Pakistan, but these are relatively more prominent while comparing the four countries in the UK: England, Wales, Scotland and Northern Ireland. In England, national curriculum tests at different grade levels are statutory; both in England and Wales teachers’ induction and inspection of schools are more structured than in Ireland and Scotland. The length of first degree programmes is usually one year more in Scotland than other three countries in the UK. In Pakistan, education system is relatively more alike across the four provinces due to uniform national curricula and policy formulation at federal level. The continuous assessment system from grade 1-12 is relatively more structured in Punjab. The overall achievement level of students is relatively high in Sindh, Punjab and NWFP lie in the middle; and Balochistan and other regions ranked at the lowest. Low achievement in English and mathematics is a common feature in Pakistan and the UK. Key Words: Education system, inter-provincial, inter-countries comparison. Background International comparisons in education and training are of great importance to understand the recent innovations and developments in countries.
    [Show full text]
  • Journal of Educational Research Departmentof
    JOURNAL OF EDUCATIONAL RESEARCH ISSN 1027-9776 (Print) ISSN 2309-8554 (Online) Vol. 20 No. 2 2017 (HEC RECOGNIZED Y CATEGORY JOURNAL) DEPARTMENTOF EDUCATION The Islamia University of Bahawalpur PAKISTAN DEPARTMENT OF EDUCATION The Islamia University of Bahawalpur PAKISTAN JOURNAL OF EDUCATIONAL RESEARCH ISSN 1027-9776 (Print) ISSN 2309-8554 (Online) Vol. 20 No. 2 2017 INDEXED IN i DEPARTMENT OF EDUCATION The Islamia University of Bahawalpur PAKISTAN JOURNAL OF EDUCATIONAL RESEARCH ISSN 1027-9776 (Print) ISSN 2309-8554 (Online) Vol. 20 No. 2 2017 EDITORIAL BOARD PATRON Professor Dr. Qaiser Mushtaq Vice Chancellor Editor Professor Dr. Akhtar Ali Dean, Faculty of Education Members Dr. Nasreen Akhtar Department of Education Dr. Sabiha Hameed Rehmani Department of Education Dr. Irshad Hussain Department of Educational Training Dr. Muhammad Ramzan Department of Educational Training Note Views expressed in the articles of this journal are of authors and do not reflect the views of the Journal of Educational Research. SUBSCRIPTION Annual Rs.200/- Single Copy Rs.100/- Special Issue Rs.150/- FOREIGN Individuals US$15.00 Annual Libraries US$10.00 Single copy Institutions US$12.00 Special Issue US$10.00 ii EDITORIAL BOARD 1. Professor Dr. Divya Jindal Snape Professor of Education, Inclusion and Life Transition, Associate Dean Research, University of Dundee, UK 2. Professor Dr. William Bill Gulam Salford University, Manchester, UK 3. Professor Dr. Riaz Ul Haq Tariq Chairman National Islamabad Accreditation Council for Teacher Education, Islamabad 4. Professor Dr. Neil Taylor School of Education, University of New England, Armidale, Australia 5. Professor Dr. Nasir Mehmood Dean, Faculty of Education, AIOU, Islamabad 6.
    [Show full text]
  • University of Education Lahore
    A COMPARATIVE STUDY OF CONTRACTUAL AND REGULAR TEACHERS’ PROFESSIONAL ATTITUDE TOWARDS JOB SATISFACTION AND JOB PERFORMANCE NASIR MAHMOOD Reg. No. 0499041 DIVISION OF EDUCATION UNIVERSITY OF EDUCATION LAHORE 2011 A COMPARATIVE STUDY OF CONTRACTUAL AND REGULAR TEACHERS’ PROFESSIONAL ATTITUDE TOWARDS JOB SATISFACTION AND JOB PERFORMANCE NASIR MAHMOOD Reg. No. 0499041 Submitted in partial fulfillment of the requirement for the degree of Doctor of Philosophy in Education at the Division of Education, University of Education, Lahore 2011 ii iii DEDICATION Dedicated to my parents, especially my mother (Late, may Allah rest her soul in peace and calm) a very pious and nice lady and very kind to me, whose prayers and affections are the source of strength and impetus for me in every step of life. My success is really the fruit of their devoted prayers and the blessings of Almighty Allah. iv PhD Thesis Certificate of Acceptance Name of Student Student No. Programme Nasir Mahmood 03-PhD-097 PhD (Education) TOPIC: A COMPARATIVE STUDY OF CONTRACTUAL AND REGULAR TEACHERS’ PROFESSIONAL ATTITUDE TOWARDS JOB SATISFACTION AND JOB PERFORMANCE Date of Acceptance: d-m-y THESIS COMMITTEE SR. # NAME POSITION SIGNATURE 1. 2. 3. 4. 5. v ACKNOWLEDGEMENT The researcher offers his most modest and honest thanks to Almighty Allah, the most compassionate and merciful, whose bounteous blessings enabled him with the potential and ability to make some contribution to the already existing ocean of knowledge in the realm of education. The researcher greatly appreciates the encouragement and commitment of his research supervisor, Dr. Muhammad Saeed for the completion of this study.
    [Show full text]