Notes for Elementary Symbolic Logic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Dyalog APL Binding Strengths
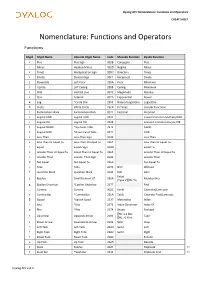
Dyalog APL Nomenclature: Functions and Operators CHEAT SHEET Nomenclature: Functions and Operators Functions Glyph Glyph Name Unicode Glyph Name Code Monadic Function Dyadic Function + Plus Plus Sign 002B Conjugate Plus - Minus Hyphen-Minus 002D Negate Minus × Times Multiplication Sign 00D7 Direction Times ÷ Divide Division Sign 00F7 Reciprocal Divide ⌊ Downstile Left Floor 230A Floor Minimum ⌈ Upstile Left Ceiling 2308 Ceiling Maximum | Stile Vertical Line 007C Magnitude Residue * Star Asterisk 002A Exponential Power ⍟ Log *Circle Star 235F Natural Logarithm Logarithm ○ Circle White Circle 25CB Pi Times Circular Functions ! Exclamation Mark Exclamation Mark 0021 Factorial Binomial ∧ Logical AND Logical AND 2227 Lowest Common Multiple/AND ∨ Logical OR Logical OR 2228 Greatest Common Divisor/OR ⍲ Logical NAND *Up Caret Tilde 2372 NAND ⍱ Logical NOR *Down Caret Tilde 2371 NOR < Less Than Less-Than Sign 003C Less Than ≤ Less Than Or Equal To Less-Than Or Equal To 2264 Less Than Or Equal To = Equal Equals Sign 003D Equal To ≥ Greater Than Or Equal To Great-Than Or Equal To 2265 Greater Than Or Equal To > Greater Than Greater-Than Sign 003E Greater Than ≠ Not Equal Not Equal To 2260 Not Equal To ~ Tilde Tilde 007E NOT Without ? Question Mark Question Mark 003F Roll Deal Enlist ∊ Epsilon Small Element Of 220A Membership (Type if ⎕ML=0) ⍷ Epsilon Underbar *Epsilon Underbar 2377 Find , Comma Comma 002C Ravel Catenate/Laminate ⍪ Comma Bar *Comma Bar 236A Table Catenate First/Laminate ⌷ Squad *Squish Quad 2337 Materialise Index ⍳ Iota *Iota 2373 -

The Unicode Cookbook for Linguists: Managing Writing Systems Using Orthography Profiles
Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2017 The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles Moran, Steven ; Cysouw, Michael DOI: https://doi.org/10.5281/zenodo.290662 Posted at the Zurich Open Repository and Archive, University of Zurich ZORA URL: https://doi.org/10.5167/uzh-135400 Monograph The following work is licensed under a Creative Commons: Attribution 4.0 International (CC BY 4.0) License. Originally published at: Moran, Steven; Cysouw, Michael (2017). The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles. CERN Data Centre: Zenodo. DOI: https://doi.org/10.5281/zenodo.290662 The Unicode Cookbook for Linguists Managing writing systems using orthography profiles Steven Moran & Michael Cysouw Change dedication in localmetadata.tex Preface This text is meant as a practical guide for linguists, and programmers, whowork with data in multilingual computational environments. We introduce the basic concepts needed to understand how writing systems and character encodings function, and how they work together. The intersection of the Unicode Standard and the International Phonetic Al- phabet is often not met without frustration by users. Nevertheless, thetwo standards have provided language researchers with a consistent computational architecture needed to process, publish and analyze data from many different languages. We bring to light common, but not always transparent, pitfalls that researchers face when working with Unicode and IPA. Our research uses quantitative methods to compare languages and uncover and clarify their phylogenetic relations. However, the majority of lexical data available from the world’s languages is in author- or document-specific orthogra- phies. -

The Unicode Standard 5.2 Code Charts
Miscellaneous Technical Range: 2300–23FF The Unicode Standard, Version 5.2 This file contains an excerpt from the character code tables and list of character names for The Unicode Standard, Version 5.2. Characters in this chart that are new for The Unicode Standard, Version 5.2 are shown in conjunction with any existing characters. For ease of reference, the new characters have been highlighted in the chart grid and in the names list. This file will not be updated with errata, or when additional characters are assigned to the Unicode Standard. See http://www.unicode.org/errata/ for an up-to-date list of errata. See http://www.unicode.org/charts/ for access to a complete list of the latest character code charts. See http://www.unicode.org/charts/PDF/Unicode-5.2/ for charts showing only the characters added in Unicode 5.2. See http://www.unicode.org/Public/5.2.0/charts/ for a complete archived file of character code charts for Unicode 5.2. Disclaimer These charts are provided as the online reference to the character contents of the Unicode Standard, Version 5.2 but do not provide all the information needed to fully support individual scripts using the Unicode Standard. For a complete understanding of the use of the characters contained in this file, please consult the appropriate sections of The Unicode Standard, Version 5.2, online at http://www.unicode.org/versions/Unicode5.2.0/, as well as Unicode Standard Annexes #9, #11, #14, #15, #24, #29, #31, #34, #38, #41, #42, and #44, the other Unicode Technical Reports and Standards, and the Unicode Character Database, which are available online. -

ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29
ISO INTERNATIONAL ORGANIZATION FOR STANDARDIZATION ORGANISATION INTERNATIONALE DE NORMALISATION --------------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 Universal Multiple-Octet Coded Character Set (UCS) -------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29 TITLE: ISO/IEC 10646-1 Second Edition text, Draft 2 SOURCE: Bruce Paterson, project editor STATUS: Working paper of JTC1/SC2/WG2 ACTION: For review and comment by WG2 DISTRIBUTION: Members of JTC1/SC2/WG2 1. Scope This paper provides a second draft of the text sections of the Second Edition of ISO/IEC 10646-1. It replaces the previous paper WG2 N 1796 (1998-06-01). This draft text includes: - Clauses 1 to 27 (replacing the previous clauses 1 to 26), - Annexes A to R (replacing the previous Annexes A to T), and is attached here as “Draft 2 for ISO/IEC 10646-1 : 1999” (pages ii & 1 to 77). Published and Draft Amendments up to Amd.31 (Tibetan extended), Technical Corrigenda nos. 1, 2, and 3, and editorial corrigenda approved by WG2 up to 1999-03-15, have been applied to the text. The draft does not include: - character glyph tables and name tables (these will be provided in a separate WG2 document from AFII), - the alphabetically sorted list of character names in Annex E (now Annex G), - markings to show the differences from the previous draft. A separate WG2 paper will give the editorial corrigenda applied to this text since N 1796. The editorial corrigenda are as agreed at WG2 meetings #34 to #36. Editorial corrigenda applicable to the character glyph tables and name tables, as listed in N1796 pages 2 to 5, have already been applied to the draft character tables prepared by AFII. -

ISO/IEC International Standard 10646-1
ISO/IEC 10646:2003/Amd.6:2009(E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 6: Bamum, Javanese, Lisu, Meetei Mayek, Samaritan, and other characters Page 2, Clause 3, Normative references Click on this highlighted text to access the reference file. Update the reference to the Unicode Bidirectional Algo- NOTE 5 – The content is also available as a separate view- rithm and the Unicode Normalization Forms as follows: able file in the same file directory as this document. The file is named: “CJKU_SR.txt”. Unicode Standard Annex, UAX#9, The Unicode Bidi- rectional Algorithm: Page 25, Clause 29, Named UCS Sequence http://www.unicode.org/reports/tr9/tr9-21.html. Identifiers Unicode Standard Annex, UAX#15, Unicode Normali- Insert the additional 290 sequence identifiers zation Forms: http://www.unicode.org/reports/tr15/tr15-31.html. <0B95, 0BCD> TAMIL CONSONANT K <0B99, 0BCD> TAMIL CONSONANT NG Page 14, Sub-clause 20.3, Format characters <0B9A, 0BCD> TAMIL CONSONANT C <0B9E, 0BCD> TAMIL CONSONANT NY Insert the following entry in the list of formats charac- <0B9F, 0BCD> TAMIL CONSONANT TT ters: <0BA3, 0BCD> TAMIL CONSONANT NN <0BA4, 0BCD> TAMIL CONSONANT T 110BD KAITHI NUMBER SIGN <0BA8, 0BCD> TAMIL CONSONANT N <0BAA, 0BCD> TAMIL CONSONANT P Page 20, Sub-clause 26.1, Hangul syllable <0BAE, 0BCD> TAMIL CONSONANT M composition method <0BAF, 0BCD> TAMIL CONSONANT Y <0BB0, 0BCD> TAMIL CONSONANT R <0BB2, 0BCD> TAMIL CONSONANT L Insert the following note after Note 2. <0BB5, 0BCD> TAMIL CONSONANT V NOTE 3 – Hangul text can be represented in several differ- <0BB4, 0BCD> TAMIL CONSONANT LLL ent ways in this standard. -

Universal Multiple-Octet Coded Character Set (UCS) —
ISO/IEC JTC1 SC2/WG2 N2845 all Final Proposed Draft Amendment (FPDAM) 1 ISO/IEC 10646:2003/Amd.1:2004 (E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 1: Glagolitic, Coptic, Georgian and other characters In the definition of Graphic character (formerly sub- Page 1, Clause 1 Scope clause 4.20, now 4.22), insert “or a format character” In the note, update the Unicode Standard version after “control function”. from 4.0 to 4.1. Page 2, Clause 3 Normative references Page 14, Clause 19 Characters in bidirectional context Update the reference to the Unicode Bidirectional Algorithm and the Unicode Normalization Forms as Add ‘Mirrored’ before ‘Character’ in clause title and follows: replace the text of the clause by the following: Unicode Standard Annex, UAX#9, The Unicode Bidi- A class of character has special significance in the rectional Algorithm, Version 4.1.0, [date TBD]. context of bidirectional text. The interpretation and rendering of any of these characters depend on the Unicode Standard Annex, UAX#15, Unicode Nor- state related to the symmetric swapping characters malization Forms, Version 4.1.0, [date TBD]. (see clause F.2.2) and on the direction of the char- acter being rendered that are in effect at the point in the CC-data-element where the coded representa- Page 2, Clause Terms and definitions tion of the character appears. The list of these char- Insert the following text as sub-clause 4.1 and Note; acters is provided in Annex E.1. update all following sub-clause numbers accord- NOTE – That list also represents all characters which have ingly. -

1 Symbols (2286)
1 Symbols (2286) USV Symbol Macro(s) Description 0009 \textHT <control> 000A \textLF <control> 000D \textCR <control> 0022 ” \textquotedbl QUOTATION MARK 0023 # \texthash NUMBER SIGN \textnumbersign 0024 $ \textdollar DOLLAR SIGN 0025 % \textpercent PERCENT SIGN 0026 & \textampersand AMPERSAND 0027 ’ \textquotesingle APOSTROPHE 0028 ( \textparenleft LEFT PARENTHESIS 0029 ) \textparenright RIGHT PARENTHESIS 002A * \textasteriskcentered ASTERISK 002B + \textMVPlus PLUS SIGN 002C , \textMVComma COMMA 002D - \textMVMinus HYPHEN-MINUS 002E . \textMVPeriod FULL STOP 002F / \textMVDivision SOLIDUS 0030 0 \textMVZero DIGIT ZERO 0031 1 \textMVOne DIGIT ONE 0032 2 \textMVTwo DIGIT TWO 0033 3 \textMVThree DIGIT THREE 0034 4 \textMVFour DIGIT FOUR 0035 5 \textMVFive DIGIT FIVE 0036 6 \textMVSix DIGIT SIX 0037 7 \textMVSeven DIGIT SEVEN 0038 8 \textMVEight DIGIT EIGHT 0039 9 \textMVNine DIGIT NINE 003C < \textless LESS-THAN SIGN 003D = \textequals EQUALS SIGN 003E > \textgreater GREATER-THAN SIGN 0040 @ \textMVAt COMMERCIAL AT 005C \ \textbackslash REVERSE SOLIDUS 005E ^ \textasciicircum CIRCUMFLEX ACCENT 005F _ \textunderscore LOW LINE 0060 ‘ \textasciigrave GRAVE ACCENT 0067 g \textg LATIN SMALL LETTER G 007B { \textbraceleft LEFT CURLY BRACKET 007C | \textbar VERTICAL LINE 007D } \textbraceright RIGHT CURLY BRACKET 007E ~ \textasciitilde TILDE 00A0 \nobreakspace NO-BREAK SPACE 00A1 ¡ \textexclamdown INVERTED EXCLAMATION MARK 00A2 ¢ \textcent CENT SIGN 00A3 £ \textsterling POUND SIGN 00A4 ¤ \textcurrency CURRENCY SIGN 00A5 ¥ \textyen YEN SIGN 00A6 -

Modernism and Mathematics
TIM ARMSTRONG “A Transfinite Syntax”: Modernism and Mathematics “Surely infiniteness is the most evident thing in the world”1 – George Oppen In modernist studies, we are familiar with aCCounts of the impaCt of turn-of-the- century physics on literature. A list would include the influence of relativity and spaCe-time distortion on representation in the arts and literary Culture; the impaCt of X-rays and nuclear fission on ideas of the material and immaterial; and the influenCe of eleCtromagnetism on notions of field theory.2 In similar ways, the impaCt of post-Darwinian biology on literature has often been traCed. 3 In contrast, it has always intrigued me that the turn of the Century also saw a revolution in mathematical thinking, less-noticed in terms of its cultural correlatives and less directly related to the physical world.4 The work of David Hilbert, RiChard Dedekind, Georg Cantor, and others in number theory seemed to offer solutions to some of the major problems inherited from the Greeks—the problem of infinitesimals and infinity generally, which calculus had largely suppressed; and the problem of the Continuity of the number line (that is, of reConCiling Continuity with the discrete nature of any point on the line, a problem 1 George Oppen, New Collected Poems, ed. MiChael Davidson, intro. Eliot Weinberger (New York: New DireCtions, 2002), 184. Subsequently referred to in text as NCP. 2 The literature here is too extensive to readily survey: for a useful reCent overview see the introduCtion of RaChel Crossland, Modernist Physics: Waves, Particles and Relativities in the Writings of Virginia Woolf and D. -

Miscellaneous Mathematical Symbols-A Range: 27C0–27EF
Miscellaneous Mathematical Symbols-A Range: 27C0–27EF This file contains an excerpt from the character code tables and list of character names for The Unicode Standard, Version 14.0 This file may be changed at any time without notice to reflect errata or other updates to the Unicode Standard. See https://www.unicode.org/errata/ for an up-to-date list of errata. See https://www.unicode.org/charts/ for access to a complete list of the latest character code charts. See https://www.unicode.org/charts/PDF/Unicode-14.0/ for charts showing only the characters added in Unicode 14.0. See https://www.unicode.org/Public/14.0.0/charts/ for a complete archived file of character code charts for Unicode 14.0. Disclaimer These charts are provided as the online reference to the character contents of the Unicode Standard, Version 14.0 but do not provide all the information needed to fully support individual scripts using the Unicode Standard. For a complete understanding of the use of the characters contained in this file, please consult the appropriate sections of The Unicode Standard, Version 14.0, online at https://www.unicode.org/versions/Unicode14.0.0/, as well as Unicode Standard Annexes #9, #11, #14, #15, #24, #29, #31, #34, #38, #41, #42, #44, #45, and #50, the other Unicode Technical Reports and Standards, and the Unicode Character Database, which are available online. See https://www.unicode.org/ucd/ and https://www.unicode.org/reports/ A thorough understanding of the information contained in these additional sources is required for a successful implementation. -

The Brill Typeface User Guide & Complete List of Characters
The Brill Typeface User Guide & Complete List of Characters Version 2.06, October 31, 2014 Pim Rietbroek Preamble Few typefaces – if any – allow the user to access every Latin character, every IPA character, every diacritic, and to have these combine in a typographically satisfactory manner, in a range of styles (roman, italic, and more); even fewer add full support for Greek, both modern and ancient, with specialised characters that papyrologists and epigraphers need; not to mention coverage of the Slavic languages in the Cyrillic range. The Brill typeface aims to do just that, and to be a tool for all scholars in the humanities; for Brill’s authors and editors; for Brill’s staff and service providers; and finally, for anyone in need of this tool, as long as it is not used for any commercial gain.* There are several fonts in different styles, each of which has the same set of characters as all the others. The Unicode Standard is rigorously adhered to: there is no dependence on the Private Use Area (PUA), as it happens frequently in other fonts with regard to characters carrying rare diacritics or combinations of diacritics. Instead, all alphabetic characters can carry any diacritic or combination of diacritics, even stacked, with automatic correct positioning. This is made possible by the inclusion of all of Unicode’s combining characters and by the application of extensive OpenType Glyph Positioning programming. Credits The Brill fonts are an original design by John Hudson of Tiro Typeworks. Alice Savoie contributed to Brill bold and bold italic. The black-letter (‘Fraktur’) range of characters was made by Karsten Lücke. -

Itherm® 280 International Version Programmer’S Guide
iTherm® 280 International Version Programmer’s Guide PN 28-07764 Rev D April 2011 This page intentionally left blank Change History Rev A Initial Release Rev B Sept 2007 Added Periodic status back Added user defined code page description. Added double byte code page support Rev C April 2009 Revised Page mode section Added several internal code pages Added Multi-byte Code page support Rev D Pg 14 Warranty 36 month was 24 April 2011 28-07764 Rev D Page 1 Federal Communications Commission Radio Frequency Interference Statement The iTherm® 280 Printer complies with the limits for a Class A computing device in accordance with the specifications in Part 15 of FCC rules. These regulations are designed to minimize radio frequency interference during installation; however, there is no guarantee that radio or television interference will not occur during any particular installation. Interference can be determined by turning the equipment off and on while the radio or television is on. If the printer causes interference to radio or television reception, try to correct the interference by one or more of the following measures: 1. Reorient the radio or television receiving antenna 2. Relocate the printer with respect to the receiver 3. Plug the printer and receiver into different circuits If necessary, the user should consult their dealer or an experienced radio/television technician for additional suggestions. The user may find the following booklet prepared by the Federal Communications Commission helpful: How to Identify and Resolve Radio/TV Interference Problems. This booklet is available from the US Government Printing Office, Washington, DC 20402. -

1 Symbols (2284)
1 Symbols (2284) USV Symbol Macro(s) Description 0009 \textHT <control> 000A \textLF <control> 000D \textCR <control> 0022 ” \textquotedbl QUOTATION MARK 0023 # \texthash NUMBER SIGN \textnumbersign 0024 $ \textdollar DOLLAR SIGN 0025 % \textpercent PERCENT SIGN 0026 & \textampersand AMPERSAND 0027 ’ \textquotesingle APOSTROPHE 0028 ( \textparenleft LEFT PARENTHESIS 0029 ) \textparenright RIGHT PARENTHESIS 002A * \textasteriskcentered ASTERISK 002B + \textMVPlus PLUS SIGN 002C , \textMVComma COMMA 002D - \textMVMinus HYPHEN-MINUS 002E . \textMVPeriod FULL STOP 002F / \textMVDivision SOLIDUS 0030 0 \textMVZero DIGIT ZERO 0031 1 \textMVOne DIGIT ONE 0032 2 \textMVTwo DIGIT TWO 0033 3 \textMVThree DIGIT THREE 0034 4 \textMVFour DIGIT FOUR 0035 5 \textMVFive DIGIT FIVE 0036 6 \textMVSix DIGIT SIX 0037 7 \textMVSeven DIGIT SEVEN 0038 8 \textMVEight DIGIT EIGHT 0039 9 \textMVNine DIGIT NINE 003C < \textless LESS-THAN SIGN 003D = \textequals EQUALS SIGN 003E > \textgreater GREATER-THAN SIGN 0040 @ \textMVAt COMMERCIAL AT 005C \ \textbackslash REVERSE SOLIDUS 005E ^ \textasciicircum CIRCUMFLEX ACCENT 005F _ \textunderscore LOW LINE 0060 ‘ \textasciigrave GRAVE ACCENT 0067 g \textg LATIN SMALL LETTER G 007B { \textbraceleft LEFT CURLY BRACKET 007C | \textbar VERTICAL LINE 007D } \textbraceright RIGHT CURLY BRACKET 007E ~ \textasciitilde TILDE 00A0 \nobreakspace NO-BREAK SPACE 00A1 ¡ \textexclamdown INVERTED EXCLAMATION MARK 00A2 ¢ \textcent CENT SIGN 00A3 £ \textsterling POUND SIGN 00A4 ¤ \textcurrency CURRENCY SIGN 00A5 ¥ \textyen YEN SIGN 00A6