Modernism and Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Addison Street Poetry Walk
THE ADDISON STREET ANTHOLOGY BERKELEY'S POETRY WALK EDITED BY ROBERT HASS AND JESSICA FISHER HEYDAY BOOKS BERKELEY, CALIFORNIA CONTENTS Acknowledgments xi Introduction I NORTH SIDE of ADDISON STREET, from SHATTUCK to MILVIA Untitled, Ohlone song 18 Untitled, Yana song 20 Untitied, anonymous Chinese immigrant 22 Copa de oro (The California Poppy), Ina Coolbrith 24 Triolet, Jack London 26 The Black Vulture, George Sterling 28 Carmel Point, Robinson Jeffers 30 Lovers, Witter Bynner 32 Drinking Alone with the Moon, Li Po, translated by Witter Bynner and Kiang Kang-hu 34 Time Out, Genevieve Taggard 36 Moment, Hildegarde Flanner 38 Andree Rexroth, Kenneth Rexroth 40 Summer, the Sacramento, Muriel Rukeyser 42 Reason, Josephine Miles 44 There Are Many Pathways to the Garden, Philip Lamantia 46 Winter Ploughing, William Everson 48 The Structure of Rime II, Robert Duncan 50 A Textbook of Poetry, 21, Jack Spicer 52 Cups #5, Robin Blaser 54 Pre-Teen Trot, Helen Adam , 56 A Strange New Cottage in Berkeley, Allen Ginsberg 58 The Plum Blossom Poem, Gary Snyder 60 Song, Michael McClure 62 Parachutes, My Love, Could Carry Us Higher, Barbara Guest 64 from Cold Mountain Poems, Han Shan, translated by Gary Snyder 66 Untitled, Larry Eigner 68 from Notebook, Denise Levertov 70 Untitied, Osip Mandelstam, translated by Robert Tracy 72 Dying In, Peter Dale Scott 74 The Night Piece, Thorn Gunn 76 from The Tempest, William Shakespeare 78 Prologue to Epicoene, Ben Jonson 80 from Our Town, Thornton Wilder 82 Epilogue to The Good Woman of Szechwan, Bertolt Brecht, translated by Eric Bentley 84 from For Colored Girls Who Have Considered Suicide I When the Rainbow Is Enuf, Ntozake Shange 86 from Hydriotaphia, Tony Kushner 88 Spring Harvest of Snow Peas, Maxine Hong Kingston 90 Untitled, Sappho, translated by Jim Powell 92 The Child on the Shore, Ursula K. -

April 2005 Updrafts
Chaparral from the California Federation of Chaparral Poets, Inc. serving Californiaupdr poets for over 60 yearsaftsVolume 66, No. 3 • April, 2005 President Ted Kooser is Pulitzer Prize Winner James Shuman, PSJ 2005 has been a busy year for Poet Laureate Ted Kooser. On April 7, the Pulitzer commit- First Vice President tee announced that his Delights & Shadows had won the Pulitzer Prize for poetry. And, Jeremy Shuman, PSJ later in the week, he accepted appointment to serve a second term as Poet Laureate. Second Vice President While many previous Poets Laureate have also Katharine Wilson, RF Winners of the Pulitzer Prize receive a $10,000 award. Third Vice President been winners of the Pulitzer, not since 1947 has the Pegasus Buchanan, Tw prize been won by the sitting laureate. In that year, A professor of English at the University of Ne- braska-Lincoln, Kooser’s award-winning book, De- Fourth Vice President Robert Lowell won— and at the time the position Eric Donald, Or was known as the Consultant in Poetry to the Li- lights & Shadows, was published by Copper Canyon Press in 2004. Treasurer brary of Congress. It was not until 1986 that the po- Ursula Gibson, Tw sition became known as the Poet Laureate Consult- “I’m thrilled by this,” Kooser said shortly after Recording Secretary ant in Poetry to the Library of Congress. the announcement. “ It’s something every poet dreams Lee Collins, Tw The 89th annual prizes in Journalism, Letters, of. There are so many gifted poets in this country, Corresponding Secretary Drama and Music were announced by Columbia Uni- and so many marvelous collections published each Dorothy Marshall, Tw versity. -
Dyalog APL Binding Strengths
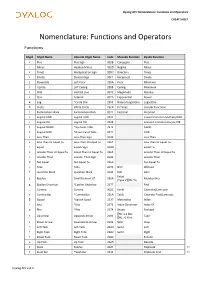
Dyalog APL Nomenclature: Functions and Operators CHEAT SHEET Nomenclature: Functions and Operators Functions Glyph Glyph Name Unicode Glyph Name Code Monadic Function Dyadic Function + Plus Plus Sign 002B Conjugate Plus - Minus Hyphen-Minus 002D Negate Minus × Times Multiplication Sign 00D7 Direction Times ÷ Divide Division Sign 00F7 Reciprocal Divide ⌊ Downstile Left Floor 230A Floor Minimum ⌈ Upstile Left Ceiling 2308 Ceiling Maximum | Stile Vertical Line 007C Magnitude Residue * Star Asterisk 002A Exponential Power ⍟ Log *Circle Star 235F Natural Logarithm Logarithm ○ Circle White Circle 25CB Pi Times Circular Functions ! Exclamation Mark Exclamation Mark 0021 Factorial Binomial ∧ Logical AND Logical AND 2227 Lowest Common Multiple/AND ∨ Logical OR Logical OR 2228 Greatest Common Divisor/OR ⍲ Logical NAND *Up Caret Tilde 2372 NAND ⍱ Logical NOR *Down Caret Tilde 2371 NOR < Less Than Less-Than Sign 003C Less Than ≤ Less Than Or Equal To Less-Than Or Equal To 2264 Less Than Or Equal To = Equal Equals Sign 003D Equal To ≥ Greater Than Or Equal To Great-Than Or Equal To 2265 Greater Than Or Equal To > Greater Than Greater-Than Sign 003E Greater Than ≠ Not Equal Not Equal To 2260 Not Equal To ~ Tilde Tilde 007E NOT Without ? Question Mark Question Mark 003F Roll Deal Enlist ∊ Epsilon Small Element Of 220A Membership (Type if ⎕ML=0) ⍷ Epsilon Underbar *Epsilon Underbar 2377 Find , Comma Comma 002C Ravel Catenate/Laminate ⍪ Comma Bar *Comma Bar 236A Table Catenate First/Laminate ⌷ Squad *Squish Quad 2337 Materialise Index ⍳ Iota *Iota 2373 -

The Unicode Cookbook for Linguists: Managing Writing Systems Using Orthography Profiles
Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2017 The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles Moran, Steven ; Cysouw, Michael DOI: https://doi.org/10.5281/zenodo.290662 Posted at the Zurich Open Repository and Archive, University of Zurich ZORA URL: https://doi.org/10.5167/uzh-135400 Monograph The following work is licensed under a Creative Commons: Attribution 4.0 International (CC BY 4.0) License. Originally published at: Moran, Steven; Cysouw, Michael (2017). The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles. CERN Data Centre: Zenodo. DOI: https://doi.org/10.5281/zenodo.290662 The Unicode Cookbook for Linguists Managing writing systems using orthography profiles Steven Moran & Michael Cysouw Change dedication in localmetadata.tex Preface This text is meant as a practical guide for linguists, and programmers, whowork with data in multilingual computational environments. We introduce the basic concepts needed to understand how writing systems and character encodings function, and how they work together. The intersection of the Unicode Standard and the International Phonetic Al- phabet is often not met without frustration by users. Nevertheless, thetwo standards have provided language researchers with a consistent computational architecture needed to process, publish and analyze data from many different languages. We bring to light common, but not always transparent, pitfalls that researchers face when working with Unicode and IPA. Our research uses quantitative methods to compare languages and uncover and clarify their phylogenetic relations. However, the majority of lexical data available from the world’s languages is in author- or document-specific orthogra- phies. -

Reading Stephen King: Issues of Censorship, Student Choice, and Popular Literature
DOCUMENT RESUME ED 414 606 CS 216 137 AUTHOR Power, Brenda Miller, Ed.; Wilhelm, Jeffrey D., Ed.; Chandler, Kelly, Ed. TITLE Reading Stephen King: Issues of Censorship, Student Choice, and Popular Literature. INSTITUTION National Council of Teachers of English, Urbana, IL. ISBN ISBN-0-8141-3905-1 PUB DATE 1997-00-00 NOTE 246p. AVAILABLE FROM National Council of Teachers of English, 1111 W. Kenyon Road, Urbana, IL 61801-1096 (Stock No. 39051-0015: $14.95 members, $19.95 nonmembers). PUB TYPE Collected Works - General (020) Opinion Papers (120) EDRS PRICE MF01/PC10 Plus Postage. DESCRIPTORS *Censorship; Critical Thinking; *Fiction; Literature Appreciation; *Popular Culture; Public Schools; Reader Response; *Reading Material Selection; Reading Programs; Recreational Reading; Secondary Education; *Student Participation IDENTIFIERS *Contemporary Literature; Horror Fiction; *King (Stephen); Literary Canon; Response to Literature; Trade Books ABSTRACT This collection of essays grew out of the "Reading Stephen King Conference" held at the University of Mainin 1996. Stephen King's books have become a lightning rod for the tensions around issues of including "mass market" popular literature in middle and 1.i.gh school English classes and of who chooses what students read. King's fi'tion is among the most popular of "pop" literature, and among the most controversial. These essays spotlight the ways in which King's work intersects with the themes of the literary canon and its construction and maintenance, censorship in public schools, and the need for adolescent readers to be able to choose books in school reading programs. The essays and their authors are: (1) "Reading Stephen King: An Ethnography of an Event" (Brenda Miller Power); (2) "I Want to Be Typhoid Stevie" (Stephen King); (3) "King and Controversy in Classrooms: A Conversation between Teachers and Students" (Kelly Chandler and others); (4) "Of Cornflakes, Hot Dogs, Cabbages, and King" (Jeffrey D. -

George Oppen Papers
http://oac.cdlib.org/findaid/ark:/13030/tf7f59p2k1 No online items George Oppen Papers Special Collections & Archives, UC San Diego Special Collections & Archives, UC San Diego Copyright 2005 9500 Gilman Drive La Jolla 92093-0175 [email protected] URL: http://libraries.ucsd.edu/collections/sca/index.html George Oppen Papers MSS 0016 1 Descriptive Summary Languages: English Contributing Institution: Special Collections & Archives, UC San Diego 9500 Gilman Drive La Jolla 92093-0175 Title: George Oppen Papers Identifier/Call Number: MSS 0016 Physical Description: 15 Linear feet(34 archives boxes, 1 flat box, and 1 map case folder) Date (inclusive): 1958-1984 Abstract: Literary papers of George Oppen (1908-1984), objectivist poet and winner of the Pulitzer Prize for Poetry in 1969. Materials range in date from 1958-1984 and include correspondence, manuscripts and typescripts for all the poems contained in Oppen's nine published books, drafts and fragments of unpublished poems, typescripts of published and unpublished essays, and interviews, translations, and reviews of Oppen's work. Scope and Content of Collection Literary papers of George Oppen (1908-1984), objectivist poet and winner of the Pulitzer Prize for Poetry in 1969. Materials range in date from 1958-1984 and include manuscripts and typescripts for all the poems contained in Oppen's nine published books, drafts and fragments of unpublished poems, typescripts of published and unpublished essays, transcripts of Oppen's verse, and copies of reviews of Oppen's work. Of special interest are loose leaf pages of notes, and Oppen's personal daybooks, all of which help to reveal his thinking about diverse subjects. -

The Unicode Standard 5.2 Code Charts
Miscellaneous Technical Range: 2300–23FF The Unicode Standard, Version 5.2 This file contains an excerpt from the character code tables and list of character names for The Unicode Standard, Version 5.2. Characters in this chart that are new for The Unicode Standard, Version 5.2 are shown in conjunction with any existing characters. For ease of reference, the new characters have been highlighted in the chart grid and in the names list. This file will not be updated with errata, or when additional characters are assigned to the Unicode Standard. See http://www.unicode.org/errata/ for an up-to-date list of errata. See http://www.unicode.org/charts/ for access to a complete list of the latest character code charts. See http://www.unicode.org/charts/PDF/Unicode-5.2/ for charts showing only the characters added in Unicode 5.2. See http://www.unicode.org/Public/5.2.0/charts/ for a complete archived file of character code charts for Unicode 5.2. Disclaimer These charts are provided as the online reference to the character contents of the Unicode Standard, Version 5.2 but do not provide all the information needed to fully support individual scripts using the Unicode Standard. For a complete understanding of the use of the characters contained in this file, please consult the appropriate sections of The Unicode Standard, Version 5.2, online at http://www.unicode.org/versions/Unicode5.2.0/, as well as Unicode Standard Annexes #9, #11, #14, #15, #24, #29, #31, #34, #38, #41, #42, and #44, the other Unicode Technical Reports and Standards, and the Unicode Character Database, which are available online. -

George Oppen and Lyn Hejinian
6O I rnr HUMANITIES REVIEW SPR]NG 201I pETER NrcHoLLs NUMERousNEss AND rrs Drscor{TENTS I 6l dates her interest in Oppen back to 1968, and it's clear from this material that she returned to a concentrated study of his work in the early nineties.2 The lecture, Numerousness and Its called originally'O s Affirmation'and subsequently retitled 'The Numerousi remains unpublished, but in 1998 Hejinian produced two other essays, 'Barbarism'and'Rea- Discontents: George Oppen sonl which also take Oppen as a major point of reference for her own meditations on philosophical and phenomenological conceptions of community or'numer- and Lyn Hejinian ousnessi to use Oppen's term.3 His work continues to act as a primary touchstone for Hejinian, as was clear at the 2002 Modernist Studies Association conference in Madison when she gave a paper titled'George Oppen and the Space of Appear- ancei Peter Nicholls , New York Uruversrty ln recent years, Hejinian's fascination with Oppen's work has focussed in- striking feature of Lyn Hejinian's recent work has creasingly on his long serial poem'Of Being Numerous'(she gave a whole course been her development of a series of terms which at the University of lowa based around this text in 1997). This was the title poem permeates both her poetic and critical writings: of the volume which brought Oppen the Pulitzer prize in 1969 and it remains, for words such as'incipiencei 'borderi 'reasoni dilemmai tontexti most readers, his best The Hmeities neview known work.'Of Being Numerousi which builds upon an ear, 'aporial and bccurrence' are deployed to create a termino- Volume g, lssue I lier poem called A Language of New York', has many interrelated concerns: in forty logical matrix in which ideas from theorists such as Hannah Spring 20 I I pp rjo-83 short sections it ranges over life in the contemporary metropolis. -

ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29
ISO INTERNATIONAL ORGANIZATION FOR STANDARDIZATION ORGANISATION INTERNATIONALE DE NORMALISATION --------------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 Universal Multiple-Octet Coded Character Set (UCS) -------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29 TITLE: ISO/IEC 10646-1 Second Edition text, Draft 2 SOURCE: Bruce Paterson, project editor STATUS: Working paper of JTC1/SC2/WG2 ACTION: For review and comment by WG2 DISTRIBUTION: Members of JTC1/SC2/WG2 1. Scope This paper provides a second draft of the text sections of the Second Edition of ISO/IEC 10646-1. It replaces the previous paper WG2 N 1796 (1998-06-01). This draft text includes: - Clauses 1 to 27 (replacing the previous clauses 1 to 26), - Annexes A to R (replacing the previous Annexes A to T), and is attached here as “Draft 2 for ISO/IEC 10646-1 : 1999” (pages ii & 1 to 77). Published and Draft Amendments up to Amd.31 (Tibetan extended), Technical Corrigenda nos. 1, 2, and 3, and editorial corrigenda approved by WG2 up to 1999-03-15, have been applied to the text. The draft does not include: - character glyph tables and name tables (these will be provided in a separate WG2 document from AFII), - the alphabetically sorted list of character names in Annex E (now Annex G), - markings to show the differences from the previous draft. A separate WG2 paper will give the editorial corrigenda applied to this text since N 1796. The editorial corrigenda are as agreed at WG2 meetings #34 to #36. Editorial corrigenda applicable to the character glyph tables and name tables, as listed in N1796 pages 2 to 5, have already been applied to the draft character tables prepared by AFII. -

The Mid-Twentieth-Century American Poetic Speaker in the Works of Robert Lowell, Frank O’Hara, and George Oppen
“THE OCCASION OF THESE RUSES”: THE MID-TWENTIETH-CENTURY AMERICAN POETIC SPEAKER IN THE WORKS OF ROBERT LOWELL, FRANK O’HARA, AND GEORGE OPPEN A dissertation submitted by Matthew C. Nelson In partial fulfillment for the requirements for the degree of Doctor of Philosophy In English TUFTS UNIVERSITY May 2016 ADVISER: VIRGINIA JACKSON Abstract This dissertation argues for a new history of mid-twentieth-century American poetry shaped by the emergence of the figure of the poetic speaker as a default mode of reading. Now a central fiction of lyric reading, the figure of the poetic speaker developed gradually and unevenly over the course of the twentieth century. While the field of historical poetics draws attention to alternative, non-lyric modes of address, this dissertation examines how three poets writing in this period adapted the normative fiction of the poetic speaker in order to explore new modes of address. By choosing three mid-century poets who are rarely studied beside one another, this dissertation resists the aesthetic factionalism that structures most historical models of this period. My first chapter, “Robert Lowell’s Crisis of Reading: The Confessional Subject as the Culmination of the Romantic Tradition of Poetry,” examines the origins of M.L. Rosenthal’s phrase “confessional poetry” and analyzes how that the autobiographical effect of Robert Lowell’s poetry emerges from a strange, collage-like construction of multiple texts and non- autobiographical subjects. My second chapter reads Frank O’Hara’s poetry as a form of intentionally averted communication that treats the act of writing as a surrogate for the poet’s true object of desire. -

Poem on the Page: a Collection of Broadsides
Granary Books and Jeff Maser, Bookseller are pleased to announce Poem on the Page: A Collection of Broadsides Robert Creeley. For Benny and Sabina. 15 1/8 x 15 1/8 inches. Photograph by Ann Charters. Portents 18. Portents, 1970. BROADSIDES PROLIFERATED during the small press and mimeograph era as a logical offshoot of poets assuming control of their means of publication. When technology evolved from typewriter, stencil, and mimeo machine to moveable type and sophisticated printing, broadsides provided a site for innovation with design and materials that might not be appropriate for an entire pamphlet or book; thus, they occupy a very specific place within literary and print culture. Poem on the Page: A Collection of Broadsides includes approximately 500 broadsides from a diverse range of poets, printers, designers, and publishers. It is a unique document of a particular aspect of the small press movement as well as a valuable resource for research into the intersection of poetry and printing. See below for a list of some of the poets, writers, printers, typographers, and publishers included in the collection. Selected Highlights from the Collection Lewis MacAdams. A Birthday Greeting. 11 x 17 Antonin Artaud. Indian Culture. 16 x 24 inches. inches. This is no. 90, from an unstated edition, Translated from the French by Clayton Eshleman signed. N.p., n.d. and Bernard Bador with art work by Nancy Spero. This is no. 65 from an edition of 150 numbered and signed by Eshleman and Spero. OtherWind Press, n.d. Lyn Hejinian. The Guard. 9 1/4 x 18 inches. -

Introduction
Copyrighted Material INTRODUCTION Poems, Poetry, Personhood It is time to explain myself. Let us stand up. EING NUMEROUS ADDRESSES a set of interdependent problems in the his Btory, theory, and politics of recent AngloAmerican poetry. In it, I offer a chal lenge and an alternative to a nearly unanimous literaryhistorical consensus that would divide poetry into two warring camps—postRomantic and postmodern; symbolist and constructivist; traditionalist and avantgarde—camps that would pit form against form on grounds at once aesthetic and ethical. Rather than choosing sides in this conflict or resorting the poems upon its field of battle, I argue that a more compelling history might begin by offering a revisionary account of what poetry is or can be. Poetry is not always and everywhere understood as a literary project aiming to produce a special kind of verbal artifact distinguished by its par ticular formal qualities or by its distinctive uses of language.1 Nor is it always un derstood as an aesthetic project seeking to provoke or promote a special kind of experience—of transformative beauty, for example, or of imaginative freedom—in its readers.2 Among the possible alternative ways of understanding poetry, I focus on the one that seems to me at once the most urgent and the one most fully ob scured by our current taxonomies. For a certain type of modern poet, I will argue, “poetry” names an ontological project: a civilizational wish to reground the con cept and the value of the person. This shift of emphasis, from “poems” as