Mobile Robot Localization Under Processing and Communication Constraints
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
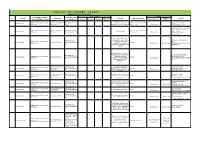
Robotics Laboratory List
Robotics List (ロボット技術関連コースのある大学) Robotics List by University Degree sought English Undergraduate / Graduate Admissions Office No. University Department Professional Keywords Application Deadline Degree in Lab links Schools / Institutes or others Website Bachelor Master’s Doctoral English Admissions Master's English Graduate School of Science and Department of Mechanical http://www.se.chiba- Robotics, Dexterous Doctoral:June and December ○ http://www.em.eng.chiba- 1 Chiba University ○ ○ ○ Engineering Engineering u.jp/en/ Manipulation, Visual Recognition Master's:June (Doctoral only) u.jp/~namiki/index-e.html Laboratory Innovative Therapeutic Engineering directed by Prof. Graduate School of Science and Department of Medical http://www.tms.chiba- Doctoral:June and December ○ 1 Chiba University ○ ○ Surgical Robotics ○ Ryoichi Nakamura Engineering Engineering u.jp/english/index.html Master's:June (Doctoral only) http://www.cfme.chiba- u.jp/~nakamura/ Micro Electro Mechanical Systems, Micro Sensors, Micro Micro System Laboratory (Dohi http://global.chuo- Graduate School of Science and Coil, Magnetic Resonance ○ ○ Lab.) 2 Chuo University Precision Mechanics u.ac.jp/english/admissio ○ ○ October Engineering Imaging, Blood Pressure (Doctoral only) (Doctoral only) http://www.msl.mech.chuo-u.ac.jp/ ns/ Measurement, Arterial Tonometry (Japanese only) Method Assistive Robotics, Human-Robot Communication, Human-Robot Human-Systems Laboratory http://global.chuo- Graduate School of Science and Collaboration, Ambient ○ http://www.mech.chuo- 2 Chuo University -

Design and Control of a Large Modular Robot Hexapod
Design and Control of a Large Modular Robot Hexapod Matt Martone CMU-RI-TR-19-79 November 22, 2019 The Robotics Institute School of Computer Science Carnegie Mellon University Pittsburgh, PA Thesis Committee: Howie Choset, chair Matt Travers Aaron Johnson Julian Whitman Submitted in partial fulfillment of the requirements for the degree of Master of Science in Robotics. Copyright © 2019 Matt Martone. All rights reserved. To all my mentors: past and future iv Abstract Legged robotic systems have made great strides in recent years, but unlike wheeled robots, limbed locomotion does not scale well. Long legs demand huge torques, driving up actuator size and onboard battery mass. This relationship results in massive structures that lack the safety, portabil- ity, and controllability of their smaller limbed counterparts. Innovative transmission design paired with unconventional controller paradigms are the keys to breaking this trend. The Titan 6 project endeavors to build a set of self-sufficient modular joints unified by a novel control architecture to create a spiderlike robot with two-meter legs that is robust, field- repairable, and an order of magnitude lighter than similarly sized systems. This thesis explores how we transformed desired behaviors into a set of workable design constraints, discusses our prototypes in the context of the project and the field, describes how our controller leverages compliance to improve stability, and delves into the electromechanical designs for these modular actuators that enable Titan 6 to be both light and strong. v vi Acknowledgments This work was made possible by a huge group of people who taught and supported me throughout my graduate studies and my time at Carnegie Mellon as a whole. -

New Method for Robotic Systems Architecture
NEW METHOD FOR ROBOTIC SYSTEMS ARCHITECTURE ANALYSIS, MODELING, AND DESIGN By LU LI Submitted in partial fulfillment of the requirements For the degree of Master of Science Thesis Advisor: Dr. Roger Quinn Department of Mechanical and Aerospace Engineering CASE WESTERN RESERVE UNIVERSITY August 2019 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of Lu Li candidate for the degree of Master of Science. Committee Chair Dr. Roger Quinn Committee Member Dr. Musa Audu Committee Member Dr. Richard Bachmann Date of Defense July 5, 2019 *We also certify that written approval has been obtained for any proprietary material contained therein. ii Table of Contents Table of Contents ................................................................................................................................................ i List of Tables ....................................................................................................................................................... ii List of Figures .................................................................................................................................................... iii Copyright page .................................................................................................................................................. iv Preface ..................................................................................................................................................................... v Acknowledgements -

KANYOK, NATHAN J., MS, December 2019 COMPUTER SCIENCE
KANYOK, NATHAN J., M.S., December 2019 COMPUTER SCIENCE SITUATIONAL AWARENESS MONITORING FOR HUMANS-IN-THE-LOOP OF TELEPRES- ENCE ROBOTIC SYSTEMS (80 pages) Thesis Advisor: Dr. Jong-Hoon Kim Autonomous automobiles are expected to be introduced in increasingly complex increments until the system is able to navigate without human interaction. However, humanity is uncomfortable with relying on algorithms to make security critical decisions, which often have moral dimensions. Many robotic systems keep humans in the decision making loop due to their unsurpassed ability to perceive contextual information in ways we find relevant. It is likely that we will see transportation systems with no direct human supervision necessary, but these systems do not address our worry about moral decisions. Until we are able to embed moral agency in digital systems, human actors will be the only agents capable of making decisions with security-critical and moral components. Additionally, in order for a human to be in the position that we can have confidence in their decision, they must be situationally aware of the environment in which the decision will be made. Virtual reality as a medium can achieve this by allowing a person to be telepresent elsewhere. A telepresence dispatch system for autonomous transportation vehicles is proposed that places emphasis on situational awareness so that humans can properly be in the decision making loop. Pre-trial, in-trial, and post-trial metrics are gathered that emphasize human health and monitor situational awareness through traditional and novel approaches. SITUATIONAL AWARENESS MONITORING FOR HUMANS-IN-THE-LOOP OF TELEPRESENCE ROBOTIC SYSTEMS A thesis submitted to Kent State University in partial fulfillment of the requirements for the degree of Master of Science by Nathan J. -

Insect-Computer Hybrid System for Autonomous Search and Rescue Mission
Insect-Computer Hybrid System for Autonomous Search and Rescue Mission Hirotaka Sato ( [email protected] ) Nanyang Technological University P. Thanh Tran-Ngoc Nanyang Technological University Le Duc Long Nanyang Technological University Bing Sheng Chong Nanyang Technological University H. Duoc Nguyen Nanyang Technological University V. Than Dung Nanyang Technological University Feng Cao Nanyang Technological University Yao Li Harbin Institute of Technology Kazuki Kai Nanyang Technological University Jia Hui Gan Nanyang Technological University T. Thang Vo-Doan University of Freiburg T. Luan Nguyen University of Leeds Physical Sciences - Article Keywords: Disaster-hit Areas, Power Consumption, Locomotion Computation Load, Obstacle-avoidance System, Navigation Control Algorithm, Human Presence Detection Posted Date: June 12th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-598481/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Insect-Computer Hybrid System for Autonomous Search and Rescue Mission P. Thanh Tran-Ngoc1, D. Long Le1, Bing Sheng Chong1, H. Duoc Nguyen1, V. Than Dung1, Feng Cao1, Yao Li2, Kazuki Kai1, Jia Hui Gan1, T. Thang Vo-Doan3, T. Luan Nguyen4, and Hirotaka Sato1* 1School of Mechanical & Aerospace Engineering, Nanyang Technological University; 50 Nanyang Avenue, 639798, Singapore 2School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen; University Town, Shenzhen, 518055, China 3University of Freiburg; Hauptstrasse. 1, Freiburg, 79104, Germany 4University of Leeds; Woodhouse, Leeds LS2 9JT, United Kingdom *Corresponding author. Email: [email protected] Abstract: There is still a long way to go before artificial mini robots are really used for search and rescue missions in disaster-hit areas due to hindrance in power consumption, computation load of the locomotion, and obstacle-avoidance system. -

Arxiv:1606.05830V4
This paper has been accepted for publication in IEEE Transactions on Robotics. DOI: 10.1109/TRO.2016.2624754 IEEE Explore: http://ieeexplore.ieee.org/document/7747236/ Please cite the paper as: C. Cadena and L. Carlone and H. Carrillo and Y. Latif and D. Scaramuzza and J. Neira and I. Reid and J.J. Leonard, “Past, Present, and Future of Simultaneous Localization And Mapping: Towards the Robust-Perception Age”, in IEEE Transactions on Robotics 32 (6) pp 1309-1332, 2016 bibtex: @articlefCadena16tro-SLAMfuture, title = fPast, Present, and Future of Simultaneous Localization And Mapping: Towards the Robust-Perception Ageg, author = fC. Cadena and L. Carlone and H. Carrillo and Y. Latif and D. Scaramuzza and J. Neira and I. Reid and J.J. Leonardg, journal = ffIEEE Transactions on Roboticsgg, year = f2016g, number = f6g, pages = f1309–1332g, volume = f32g g arXiv:1606.05830v4 [cs.RO] 30 Jan 2017 1 Past, Present, and Future of Simultaneous Localization And Mapping: Towards the Robust-Perception Age Cesar Cadena, Luca Carlone, Henry Carrillo, Yasir Latif, Davide Scaramuzza, Jose´ Neira, Ian Reid, John J. Leonard Abstract—Simultaneous Localization And Mapping (SLAM) I. INTRODUCTION consists in the concurrent construction of a model of the environment (the map), and the estimation of the state of the robot LAM comprises the simultaneous estimation of the state moving within it. The SLAM community has made astonishing S of a robot equipped with on-board sensors, and the con- progress over the last 30 years, enabling large-scale real-world struction of a model (the map) of the environment that the applications, and witnessing a steady transition of this technology to industry. -

A Novel SLAM Quality Evaluation Method
DEGREE PROJECT IN COMPUTER SCIENCE AND ENGINEERING, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2019 A Novel SLAM Quality Evaluation Method FELIX CAESAR KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL ENGINEERING AND COMPUTER SCIENCE A Novel SLAM Quality Evaluation Method FELIX CAESAR Master’s in System, Control and Robotics Date: July 1, 2019 Supervisor: Jana Tumova Examiner: John Folkesson School of Electrical Engineering and Computer Science Host company: ÅF Swedish title: En ny metod för kvalitetsbedömning av SLAM iii Abstract Autonomous vehicles have grown into a hot topic in both research and indus- try. For a vehicle to be able to run autonomously, it needs several different types of systems to function properly. One of the most important of them is simultaneous localization and mapping (SLAM). It is used for estimating the pose of the vehicle and building a map of the environment around it based on sensor readings. In this thesis we have developed an novel approach to mea- sure and evaluate the quality of a landmark-based SLAM algorithm in a static environment. The error measurement evaluation is a multi-error function and consists of the following error types: average pose error, maximum pose error, number of false negatives, number of false positives and an error relating to the distance when landmarks are added into the map. The error function can be tailored towards specific applications by settings different weights for each error. A small research concept car with several different sensors and an outside tracking system was used to create several datasets. The datasets include three different map layouts and three different power settings on the car’s engine to create a large variability in the datasets. -

Robotics 2020 Multi-Annual Roadmap
Robotics 2020 Multi-Annual Roadmap For Robotics in Europe Call 2 ICT24 (2015) – Horizon 2020 Release B 06/02/2015 Rev A: Initial release for Comment. Rev B: Final Release for Call Contents 1. Introduction ........................................................................................................... 1106H 1.1 MAR Content .............................................................................................................................. 2107H 1.2 Reading the Roadmap ............................................................................................................ 3108H 1.2.2. Why read this document? .................................................................................................................. 3109H 1.3 Understanding the MAR ........................................................................................................ 5110H 1.3.1. MAR Background ................................................................................................................................... 5111H 1.3.2. Structure of the MAR ........................................................................................................................... 5112H 1.3.3. Technical Progression in the MAR ................................................................................................. 7113H 1.3.4. Use of the MAR in Proposals ............................................................................................................. 8114H 1.3.5. Step Changes and TRLs ...................................................................................................................... -

A Taxonomy for Mobile Robots: Types, Applications, Capabilities, Implementations, Requirements, and Challenges
robotics Article A Taxonomy for Mobile Robots: Types, Applications, Capabilities, Implementations, Requirements, and Challenges Uwe Jahn 1,* , Daniel Heß 1, Merlin Stampa 1 , Andreas Sutorma 2 , Christof Röhrig 1, Peter Schulz 3 and Carsten Wolff 1 1 IDiAL Institute, Dortmund University of Applied Science and Arts, Otto-Hahn-Str. 23, 44227 Dortmund, Germany; [email protected] (D.H.); [email protected] (M.S.); [email protected] (C.R.); [email protected] (C.W.) 2 Faculty of Information Technology, Dortmund University of Applied Science and Arts, Sonnenstraße 96, 44139 Dortmund, Germany; [email protected] 3 Faculty of Engineering and Computer Science, Hamburg University of Applied Sciences, 20099 Hamburg, Germany; [email protected] * Correspondence: [email protected]; Tel.: +49-231-9112-9661 Received: 30 October 2020; Accepted: 11 December 2020; Published: 15 December 2020 Abstract: Mobile robotics is a widespread field of research, whose differentiation from general robotics is often based only on the ability to move. However, mobile robots need unique capabilities, such as the function of navigation. Also, there are limiting factors, such as the typically limited energy, which must be considered when developing a mobile robot. This article deals with the definition of an archetypal robot, which is represented in the form of a taxonomy. Types and fields of application are defined. A systematic literature review is carried out for the definition of typical capabilities and implementations, where reference systems, textbooks, and literature references are considered. Keywords: robotics; mobile robot; taxonomy; requirements; challenges; capabilities; implementations; literature review; survey 1. -

Deep Reinforcement Learning for Soft Robotic Applications: Brief Overview with Impending Challenges
Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 23 November 2018 doi:10.20944/preprints201811.0510.v2 Peer-reviewed version available at Robotics 2019, 8, 4; doi:10.3390/robotics8010004 Review Deep Reinforcement Learning for Soft Robotic Applications: Brief Overview with Impending Challenges Sarthak Bhagat 1,2,y,Hritwick Banerjee 1,3y ID , Zion Tsz Ho Tse4 and Hongliang Ren 1,3,5,* ID 1 Department of Biomedical Engineering, Faculty of Engineering, 4 Engineering Drive 3, National University of Singapore, Singapore 117583, Singapore; [email protected] (H.B.) 2 Department of Electronics and Communications Engineering, Indraprastha Institute of Information Technology, Delhi, New Delhi, Delhi 110020, India; [email protected] (S.B.) 3 Singapore Institute for Neurotechnology (SINAPSE), Centre for Life Sciences, National University of Singapore, Singapore 117456. 4 School of Electrical & Computer Engineering, College of Engineering, The University of Georgia, Athens 30602, USA; [email protected] (Z.T.H.T) 5 NUS (Suzhou) Research Institute (NUSRI), Wuzhong Dist., Suzhou City, Jiangsu Province, China. † These authors equally contributed towards this manuscript. * Correspondence: [email protected] (H.R.); Tel.: +65-6601-2802 Abstract: The increasing trend of studying the innate softness of robotic structures and amalgamating it with the benefits of the extensive developments in the field of embodied intelligence has led to sprouting of a relatively new yet extremely rewarding sphere of technology. The fusion of current deep reinforcement algorithms with physical advantages of a soft bio-inspired structure certainly directs us to a fruitful prospect of designing completely self-sufficient agents that are capable of learning from observations collected from their environment to achieve a task they have been assigned. -

IEEE EAD First Edition Committees List Table of Contents (1 January 2019)
IEEE EAD First Edition Committees List Table of Contents (1 January 2019) Please click on the links below to navigate to specific sections of this document. Executive Committee Descriptions and Members Content Committee Descriptions and Members: • General Principles • Classical Ethics in A/IS • Well-being • Affective Computing • Personal Data and Individual Agency • Methods to Guide Ethical Research and Design • A/IS for Sustainable Development • Embedding Values into Autonomous Intelligent Systems • Policy • Law • Extended Reality • Safety and Beneficence of Artificial General Intelligence (AGI) and Artificial Superintelligence (ASI) • Reframing Autonomous Weapons Systems Supporting Committee Descriptions and Members: • The Editing Committee • The Communications Committee • The Glossary Committee • The Outreach Committee A Special Thanks To: • Arabic Translation Team • China Translation Team • Japan Translation Team • South Korea Translation Team • Brazil Translation Team • Thailand Translation Team • Russian Federation Translation Team • Hong Kong Team • Listing of Contributors to Request for Feedback for EADv1 • Listing of Attendees for SEAS Events iterating EADv1 and EADv2 • All our P7000™ Working Group Chairs 1 1 January 2019 | The IEEE Global Initiative on Ethics of Autonomous and Intelligent Systems Executive Committee Descriptions & Members Raja Chatila – Executive Committee Chair, The IEEE Global Initiative on Ethics of Autonomous and Intelligent Systems Raja Chatila, IEEE Fellow, is Professor at Sorbonne Université, Paris, France , and Director of the Institute of Intelligent Systems and Robotics (ISIR). He is also Director of the Laboratory of Excellence “SMART” on human-machine interactions. His work covers several aspects of autonomous and interactive Robotics, in robot navigation and SLAM, motion planning and control, cognitive and control architectures, human-robot interaction, and robot learning, and to applications in the areas of service, field and space robotics. -

Simultaneous Localization and Mapping 46.1 SLAM: Problem Definition 1155 Ical Model for SLAM
1153 Multimedia Contents 46. Simultaneous Localization Simultaneoand Mapping u Part E | 46 Cyrill Stachniss, John J. Leonard, Sebastian Thrun 46.1 SLAM: Problem Definition..................... 1154 This chapter provides a comprehensive intro- 46.1.1 Mathematical Basis ................... 1154 duction in to the simultaneous localization and 46.1.2 Example: SLAM mapping problem, better known in its abbreviated in Landmark Worlds .................. 1155 form as SLAM. SLAM addresses the main percep- 46.1.3 Taxonomy of the SLAM Problem .. 1156 tion problem of a robot navigating an unknown environment. While navigating the environment, 46.2 The Three Main SLAM Paradigms ........... 1157 the robot seeks to acquire a map thereof, and 46.2.1 Extended Kalman Filters ............ 1157 at the same time it wishes to localize itself us- 46.2.2 Particle Methods ....................... 1159 46.2.3 Graph-Based ing its map. The use of SLAM problems can be Optimization Techniques............ 1162 motivated in two different ways: one might be in- 46.2.4 Relation of Paradigms................ 1166 terested in detailed environment models, or one might seek to maintain an accurate sense of a mo- 46.3 Visual and RGB-D SLAM ........................ 1166 bile robot’s location. SLAM serves both of these 46.4 Conclusion and Future Challenges ........ 1169 purposes. Video-References......................................... 1170 We review the three major paradigms from which many published methods for SLAM are de- References................................................... 1171 rived: (1) the extended Kalman filter (EKF); (2) particle filtering; and (3) graph optimization. We also review recent work in three-dimensional (3-D) tance-sensors (RGB-D), and close with a discussion SLAM using visual and red green blue dis- of open research problems in robotic mapping.