DOCSLIB.ORG

Renal Physiology Background

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Renal Physiology Background RENAL PHYSIOLOGY Florida State University Advanced Topics in Biomedical Mathematics MAP5932, Spring 2007 03/16/07 Brinda Pamulapati Goal 1 Background of the kidney 2 Glomerulus 3 Mathematical model of Glomerulus 4 Co-current and counter- current mechanism 5 Mathematical model of the co-current and counter-current mechanism Kidney Kidney and Nephron picture Glomerulus and Bowman's Capsule Mathematical model of the glomerular filter There are 3 pressures that effect the rate of glomerular filtration: 1 the pressure inside the glomerular capillaries that promote filteration(p1) 2 the pressure inside the Bowman's capsule that opposes filtration(p2) 3 the colloidal osmotic pressure of the plasma proteins inside the capillaries that opposes filteration(pi) Schematic diagram of the glomerular filtration(one dimentional) q2 Qi q1 Qe x=0 x=L Mathematical model of the glomerular filter(cont.) dq 1 = K (P " P + ! ) dx f 2 1 c P1 ,P2 = hydrostatic pressure ! c = osmotic pressure of the suspended protei ns and formed elements of the blood K f = capillary filteration rate where osmotic pressure is ! c = RTc Conservation Equation ciQi = cq1 ! c ciQi = q1 ( from osmosis RTc) RT ! c = ! c = RTciQi / q1 Qi ! c = ! i (where ! i = RTci ) q1 Mathematical Model of the Glomerulus dq1 = K (P " P + ! ) ................(20.1) dx f 2 1 c Qi ! c = ! i .......................................................(20.4) qi # Q $ e %! Q & Q ' " e +! ln & i ' =1% K L i f ..............(20.5) Qi & 1%! ' !Qi & ' ( ) Qe =efflux through the efferent arterioles L=length of the filter !=" i /(P1 # P2) Cocurrent and Countercurrent Mechanism What is Cocurrent and Countercurrent Mechanism Why Study about it ? The human kidney use countercurrent exchange to remove water from urine so the body can retain water that was used to move the nitrogenous waste products. Mathematical Model of the Cocurrent and Countercurrent Mechanism !C1 !C1 + q = d(C "C ) .....................(20.15) !t 1 !x 2 1 !C2 !C2 + q2 = d(C1 " C2 ) ..................(20.16) !t !x Mathematical Problem To Find: The outflow concentration Given : 1) The inflow concentration 2) The length of the exchange chamber 3) Flow velocities are known 0 0 Assume: Flows are in steady state C1 &C2 The input concentrations are COCURRENT MECHANISM C1 (L) 1+ "# 1$ " $!L 0 = + # e C1 1+ # 1+ # C 0 q d % 1 & 2 , 2 , 1 " = 0 # = ! = ' + ( C1 q1 q1 ) # * COUNTERCURRENT MECHANISM $ $!L C1 (L) $"# + (1$ # + "#)e = L 0 $ $! C1 e $ # C L C 0 q d % 1 & 2 ( ) 2 , 2 , 1 " = 0 = 0 # = $ ! = ' $ ( C1 C1 q1 q1 ) # * Conclusion Total transfer of solute is always more efficient with a countercurrent than with a cocurrent. Sources J.Keener, J.Sneyd, Mathematical Physiology http://en.wikipedia.org/wiki/Image:Kidneys_from_behind.jp g http://ocw.mit.edu/NR/rdonlyres/Health-Sciences-and Technology/HST-542JSpring-2004/BB83F266-3398- 4154-A81D- 758E76A74EB5/0/renal_physiology.pdf http://coe.fgcu.edu/faculty/greenep/kidney/index.html http://en.wikipedia.org/wiki/Countercurrent_exchange.
Load more

Recommended publications
  • Development and Structure of the Excretory System the Nephron
    Biology 224 Human Anatomy and Physiology II Week 7; Lecture 1; Monday Dr. Stuart S. Sumida Development and Structure of the Excretory System The Nephron DEVELOPMENT AND STRUCTURE OF EXCRETORY SYSTEM EXCRETORY SYSTEM REVIEW • Kidneys derived from INTERMEDIATE MESODERM. • Kidney starts out as a SEGMENTAL STRUCTURE. • Bladder, as part of embryonic gut tube: lining derived from endoderm. • Note, this is EXCRETION, NOT “ELIMINATION.” EARLY KIDNEY DEVELOPMENT • There is a segment of intermediate mesoderm for every body segment. • Earliest kidney appears in the cervical region of the body! (About week 3.) Called the PRONEPHROS. • Develop very close to the gonads. (They battle it out for the nearby ducts.) THE PRONEPHROS • The early anteriorly developed kidney parts. • Has NO EXCRETORY FUNCTION. • Functions to INDUCE DEVELOPMENT of middle segments of intermediate meosderm into the MESONEPHROS. THE MESONEPHROS • Some think it is the functioning embryonic kidney. Some think is has no excretory function. • WE DO KNOW that the duct that attaches to it (THE MESONEPHRIC DUCT) is very important in INDUCING DEVELOPMENT OF THE CAUDAL KIDNEY SEGMENTS (the METANEPHROS). Mesonephric Duct reaches all the way to end of gut tube (cloaca). We need to... • Attach the ducts to the hindend kidney (the metanephros). • Split the bladder away from the gut tube. After the mesonephric duct attaches to cloaca, the embryonic URETER grows from caudal to cranial to attach to mass of metanephric kidney. A septum, the URORECTAL SEPTUM, grows between the more dorsal part of the gut tube and the more ventral part that will become the bladder. Note that attached to the bladder are right and left ueters, the allantois (an extraembryonic membrane).
    [Show full text]
  • The Contribution of Nasal Countercurrent Heat Exchange to Water Balance in the Northern Elephant Seal, Mirounga Angustirostris
    J. exp. Biol. 113, 447-454 (1984) 447 Printed in Great Britain © The Company of Biologists Limited 1984 THE CONTRIBUTION OF NASAL COUNTERCURRENT HEAT EXCHANGE TO WATER BALANCE IN THE NORTHERN ELEPHANT SEAL, MIROUNGA ANGUSTIROSTRIS BY ANTHONY C. HUNTLEY, DANIEL P. COSTA Long Marine Laboratory, Center for Marine Studies, University of California, Santa Cruz, U.SA. AND ROBERT D. RUBIN Department of Life Sciences, Santa Rosa Junior College, Santa Rosa, California, U.SA Accepted 29 May 1984 SUMMARY 1. Elephant seals fast completely from food and water for 1-3 months during terrestrial breeding. Temporal countercurrent heat exchange in the nasal passage reduces expired air temperature (Te) below body temperature (Tb)- 2. At a mean ambient temperature of 13'7°C, Te is 20*9 °C. This results in the recovery of 71-5 % of the water added to inspired air. 3. The amount of cooling of the expired air (Tb~Te) and the percentage of water recovery varies inversely with ambient temperature. 4. Total nasal surface area available for heat and water exchange, located in the highly convoluted nasal turbinates, is estimated to be 720 cm2 in weaned pups and 3140 cm2 in an adult male. 5. Nasal temporal countercurrent heat exchange reduces total water loss sufficiently to allow maintenance of water balance using metabolic water production alone. INTRODUCTION Northern elephant seals, Mirounga angustirostis (Gill), are exceptional among pin- nipeds in the duration of their terrestrial breeding fast. During this time, they volun- tarily forgo both food and water while remaining active on the rookery. The length of these fasts varies with age, sex and social status.
    [Show full text]
  • L8-Urine Conc. [PDF]
    The loop of Henle is referred to as countercurrent multiplier and vasa recta as countercurrent exchange systems in concentrating and diluting urine. Explain what happens to osmolarity of tubular fluid in the various segments of the loop of Henle when concentrated urine is being produced. Explain the factors that determine the ability of loop of Henle to make a concentrated medullary gradient. Differentiate between water diuresis and osmotic diuresis. Appreciate clinical correlates of diabetes mellitus and diabetes insipidus. Fluid intake The total body water Antidiuretic hormone is controled by : Renal excretion of water Hyperosmolar medullary Changes in the osmolarity of tubular fluid : interstitium 1 2 3 Low osmolarity The osmolarity High osmolarity because of active decrease as it goes up because of the transport of Na+ and because of the reabsorbation of water co-transport of K+ and reabsorption of NaCl Cl- 4 5 Low osmolarity because of High osmolarity because of reabsorption of NaCl , also reabsorption of water in reabsorption of water in present of ADH , present of ADH reabsorption of urea Mechanisms responsible for creation of hyperosmolar medulla: Active Co- Facilitated diffusion transport : transport : diffusion : of : Na+ ions out of the Only of small thick portion of the K+ , Cl- and other amounts of water ascending limb of ions out of the thick from the medullary the loop of henle portion of the Of urea from the tubules into the into the medullary ascending limb of inner medullary medullary interstitium the loop of henle collecting
    [Show full text]
  • Thermal Relations 10
    CHAPTER Thermal Relations 10 s this bumblebee flies from one flower cluster to another to collect nectar and pollen, temperature matters for the bee in two crucial ways. First, the temperature of the bumblebee’s flight muscles de- A termines how much power they can generate. The flight muscles must be at least as warm as about 35°C to produce enough power to keep the bee airborne; if the muscles are cooler, the bee cannot fly. The second principal way in which temperature matters is that for a bumblebee to maintain its flight muscles at a high enough temperature to fly, the bee must expend food energy to generate heat to warm the muscles. In a warm environment, all the heat required may be produced simply as a by-product of flight. In a cool environment, however, as a bumblebee moves from flower cluster to flower cluster—stopping at each to feed—it must expend energy at an elevated rate even during the intervals when it is not flying, either to keep its flight muscles continually at a high enough temperature to fly or to rewarm the flight muscles to flight temperature if they cool while feeding. Assuming that the flight muscles must be at 35°C for flight, they must be warmed to 10°C above air temperature if the air is at 25°C, but to 30°C above air temperature if the air is at 5°C. Thus, as the air becomes cooler, a bee must expend food energy at a higher and higher rate to generate heat to warm its flight muscles to flight temperature, meaning it must collect food at a higher and higher rate.
    [Show full text]
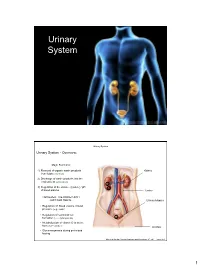
  • Urinary System
    Urinary System Urinary System Urinary System - Overview: Major Functions: 1) Removal of organic waste products Kidney from fluids (excretion) 2) Discharge of waste products into the environment (elimination) 1 3) Regulation of the volume / [solute] / pH 3 of blood plasma Ureter HOWEVER, THE KIDNEY AIN’T JUST FOR PEE’IN… Urinary bladder • Regulation of blood volume / blood pressure (e.g., renin) • Regulation of red blood cell formation (i.e., erythropoietin) 2 • Metabolization of vitamin D to active form (Ca++ uptake) Urethra • Gluconeogenesis during prolonged fasting Marieb & Hoehn (Human Anatomy and Physiology, 8th ed.) – Figure 25.1 1 Urinary System Renal ptosis: Kidneys drop to lower position due Functional Anatomy - Kidney: to loss of perirenal fat Located in the superior lumbar “Bar of soap” region 12 cm x 6 cm x 3 cm 150 g / kidney Layers of Supportive Tissue: Renal fascia: Peritoneal cavity Outer layer of dense fibrous connective tissue; anchors kidney in place Perirenal fat capsule: Fatty mass surrounding kidney; cushions kidney against blows Fibrous capsule: Transparent capsule on kidney; prevents infection of kidney from local tissues Kidneys are located retroperitoneal Marieb & Hoehn (Human Anatomy and Physiology, 8th ed.) – Figure 25.2 Urinary System Functional Anatomy - Kidney: Pyelonephritis: Inflammation of the kidney Pyramids appear striped due to parallel arrangement of capillaries / collecting tubes Renal cortex Renal medulla Renal pyramids Renal papilla Renal columns Renal hilum Renal pelvis • Entrance for blood vessels
    [Show full text]
  • Countercurrent Transport in the Kidney
    Ann. Rev. Biophys. Bioeng. 1978. 7:315-39 COUNTERCURRENT +9115 TRANSPORT IN THE KIDNEY 1 John L. Stephenson Section on Theoretical Biophysics, National Heart, Lung and Blood· Institute and Mathematical Research Branch, National Institute of Arthritis, Metabolism, and Digestive Diseases, National Institutes of Health, Bethesda, Maryland 20014 INTRODUCTION Renal physiologists recognized many years ago that the ability of a glomerular kidney to form a concentrated urine was correlated in some way with the possession of a loop of Henle (see 56). It was also recognized that more water than solute must be absorbedfrom the glomerular filtrate to produce a urine more concentrated than plasma. Smith (62, 63) quantitated the relative water reabsorption by noting that if the final urine were to be reduced to isotonicity by the addition or subtraction of water, the total solute excreted by the kidney per minute would occupy a volume of UCM!CpM, where Uis the urine flow, CM is the urine osmolality, and G],M is the plasma osmolality. Since the actual volume occupied by this solute is U. the quantity of water U - UeM! G],M would have to be subtracted when the urine is hypotonic and added when the urine is hypertonic to bring the final urine to isotonicity. Smith called this virtual volume free water for the diluting kidney and negative free water for the concentrating kidney. Since the micropunc­ ture studies of Richards and his associates had shown that the glomerular filtrate was isotonic and remained so in the proximal tubule (57, 58), it was inferred that in the concentrating kidney the absorption of water in excess of its isotonic complement of solute took place somewhere in the distal nephron.
    [Show full text]
  • Quantitation of Countercurrent Exchange During Passive Absorption from the Dog Small Intestine: Evidence for Marked Species Differences in the Efficiency of Exchange
    Quantitation of countercurrent exchange during passive absorption from the dog small intestine: evidence for marked species differences in the efficiency of exchange. J H Bond, … , D G Levitt, M D Levitt J Clin Invest. 1977;59(2):308-318. https://doi.org/10.1172/JCI108642. Research Article The present investigation was designed to quantitatively assess the possible influence of countercurrent exchange on passive absorption from the small intestine of the dog. Villus blood flow was measured with a modification of the microsphere method. Simultaneously, the absorption from the gut lumen of five diffusible gases (H2, He, CH4, 133Xe, and CO) was determined. Villus blood flow averaged 0.247 +/- 0.03 (SEM) ml/min per g. The observed absorption of H2, He, CH4, and 133Xe was only 16.2 +/- 1.8, 12.8 +/- 2.3, 12.0 +/- 1.8, and 15.8 +/- 1.4 %, respectively, of what this villus blood flow could carry away if it reached perfect equilibrium with the luminal gases. This low absorption rate could result from diffusion limitation to absorption or countercurrent exchange. The diffusive permeability of the barrier seperating the luminal gases and villus blood flow was assessed by measuring the absorption rate of CO. Because absorbed CO binds tightly to hemoglobin, it cannot exchange, and when present in low concentrations its uptake is entirely diffusion limited. Knowledge of the diffusion rate through tissue of the unbound gases relative to that of CO made it possible to calculate the degree to which each of the unbound gases should equilibrate with villus tip blood. The percentage equilibration between lumen and blood at the villus tip for H2, He, CH4, […] Find the latest version: https://jci.me/108642/pdf Quantitation of Countercurrent Exchange during Passive Absorption from the Dog Small Intestine EVIDENCE FOR MARKED SPECIES DIFFERENCES IN THE EFFICIENCY OF EXCHANGE JOHN H.
    [Show full text]
  • Heat Loss in the Carotid Artery During Selective Brain Cooling in Humans
    Heat Loss in the Carotid Artery During Selective Brain Cooling in Humans Final Project Report May 5, 2006 BEE 453 Computer-Aided Engineering: Applications to Biomedical Processes Professor Ashim Datta Suneth Attygalle Hussein Girnary Natalie Jeffrey Sean Lee Rosa Torre Page 1 of 25 TABLE OF CONTENTS Table of Contents..................................................................................................2 Executive Summary ..............................................................................................3 Introduction ...........................................................................................................4 Design Objectives .................................................................................................5 Schematic..........................................................................................................5 Results and Discussion.........................................................................................6 Qualitative Description.......................................................................................6 Sensitivity Analysis ..........................................................................................10 Conclusions and Design Recommendations.......................................................11 Analysis ...........................................................................................................11 Design Recommendations ..............................................................................12 Realistic Constraints
    [Show full text]
  • Gas Exchange
    Introduction to Biological Science - BIOL 1361 recitation Gas Exchange A. Influence of concentration gradient on gas diffusion rate 1. You have two tubes of permeable membrane. a. Add an arrow to illustrate concurrent fluid flow in Tubes A and B. Tube A Tube B b. Add an arrow to illustrate countercurrent fluid flow in Tubes A and B. Tube A Tube B c. Describe the movement of oxygen between Tube A and Tube B if the oxygen concentration in Tube A and B are the same. d. Describe the movement of O2 between Tube A and Tube B in example (a) above if the O2 concentration in the fluid entering the left end of Tube A is 120 ppm and the O2 concentration in the fluid entering the left end of Tube B is 80 ppm. What will the concentrations look like at the right end of each tube? e. Describe the movement of O2 between Tube A and Tube B in example (b) above if the O2 concentration in the fluid entering the left end of Tube A is 120 ppm and the concentration of O2 in the fluid entering the right end of Tube B is 80 ppm. What will the concentrations look like at the opposite end of each tube? Will the concentration of oxygen reach equilibrium at either end of the tubes? D. Pattison and A.O. Cheek, Department of Biological Sciences, University of Houston Rev. 7/30/15 Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0) Introduction to Biological Science - BIOL 1361 recitation 2.
    [Show full text]
  • Chapter 22: Gas Exchange
    Chapter 22: Gas Exchange Name ________________________ Period _________ Chapter 22: Gas Exchange Guided Reading Activities Big idea: Mechanisms of gas exchange Answer the following questions as you read modules 22.1–22.5: 1. Gas exchange involves three stages. List and briefly describe the three stages. Breathing—inhalation of oxygen and exhalation of carbon dioxide. Transport of gases—oxygen and carbon dioxide must be transported to and from the tissues of the body. Gas exchange with tissues of the body—oxygen and carbon dioxide must be exchanged at the cellular level. 2. Which of the following statements regarding gas exchange is correct? a. Contracting muscle tissue do not need increased amounts of O2. b. Blood that is leaving metabolically active tissues is high in O2. c. Blood that is leaving the lungs is high in O2 and low in CO2. d. Blood returning to the heart from body tissues is low in CO2. 3. A person has a mutation in a gene that leads to a decrease in the efficiency at which O2 is picked up by the blood. Would this person have difficulty doing certain activities? If so, which ones? Briefly explain your answer. This person would have difficulty doing even mild exercise or strenuous activities because his or her ability to carry oxygen would be hindered. 4. The part of an animal’s body where gas exchange occurs is known as ___________________.the respiratory surface 5. True or false: Gas exchange occurs via osmosis. If false, make it a correct statement. False, gas exchange occurs via diffusion. 134 Copyright © 2015 Pearson Education, Inc.
    [Show full text]
  • Countercurrent Flow in Biology
    Bio Factsheet www.curriculum-press.co.uk Number 160 Countercurrent Flow in Biology Countercurrent flow is a mechanism which maintains diffusion Fig 1. Countercurrent heat exchange gradients across membranes. In turn, this means that transport or exchange of substances across the membrane can be fast and efficient. This Factsheet summarises the process and describes the type of exam questions which have appeared in recent years. warm blood from heart cool Countercurrent flow is a simple concept; it is just two substances flowing through a part of the body in opposite directions. The aim artery of this opposite flow is to maintain a gradient of some sort (eg temperature gradient or concentration gradient of oxygen), which will then ensure that heat or oxygen etc is transferred efficiently vein from one to the other. warm cool blood To understand this, imagine two parallel but separate water pipes, from arranged next to each other and in contact along their length. Water extremities entering one pipe is hot, and water entering the other is cold. Heat will pass from one to the other. Now consider two situations; water flow in the same direction and When heat loss is no problem, most of the venous blood from the water flow in opposite directions extremities returns through veins located near the surface. Water flow in the same direction Countercurrent heat exchangers operate in the legs of many birds. If water flow is in the same direction, initially, the temperature Penguins, vultures, ducks and sea gulls all have them. A sea gull, difference will be at its maximum.
    [Show full text]
  • Evidence from Oxygen Isotopes. (Under the Direction of Reese Barrick.)
    ABSTRACT MISSELL, CHRISTINE ANN. Thermoregulatory adaptations of Acrocanthosaurus atokensis – evidence from oxygen isotopes. (Under the direction of Reese Barrick.) Isotopic analyses of bone phosphate oxygen from a modern alligator, ostrich, and elephant have provided a means for examining diagenesis and thermoregulatory strategy within the dinosaur Acrocanthosaurus atokensis. The Acrocanthosaurus specimen is assumed to retain an original isotopic signature, based on a lack of linear correlation 18 18 between δ Ophosphate and structural δ Ocarbonate, equal standard deviations between 18 δ Ophosphate values for spongy and compact bone, and a significant difference between 18 18 δ Ophosphate and cement δ Ocarbonate. Interbone and intrabone temperature variation patterns suggest that Acrocanthosaurus followed a homeothermic pattern of heat distribution (i.e. maintenance of a 4°C temperature range). Comparison with the modern animals yields a closer resemblance to the ostrich and elephant versus the alligator, thereby suggesting Acrocanthosaurus was endothermic. The Acrocanthosaurus sacral spines and palatal bones show evidence of use as heat shedding structures and the braincase yields a significantly higher calculated temperature than the body. THERMOREGULATORY ADAPTATIONS OF ACROCANTHOSAURUS ATOKENSIS – EVIDENCE FROM OXYGEN ISOTOPES By CHRISTINE ANN MISSELL A thesis submitted to the Graduate Faculty of North Carolina State University in partial fulfillment of the requirements for the Degree of Master of Science MARINE, EARTH, AND ATMOSPHERIC SCIENCES Raleigh 2004 APPROVED BY: ________________________ ________________________ ________________________ ________________________ Chair of Advisory Committee DEDICATION I would like to dedicate this work to my mother for teaching me the true meaning of strength, perseverance, patience, and good spelling. ii BIOGRAPHY Christine Missell was born and raised in Rochester, NY.
    [Show full text]