Mathematical Ideas in Ancient Indian Poetry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
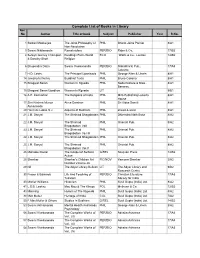
Complete List of Books in Library Acc No Author Title of Book Subject Publisher Year R.No
Complete List of Books in Library Acc No Author Title of book Subject Publisher Year R.No. 1 Satkari Mookerjee The Jaina Philosophy of PHIL Bharat Jaina Parisat 8/A1 Non-Absolutism 3 Swami Nikilananda Ramakrishna PER/BIO Rider & Co. 17/B2 4 Selwyn Gurney Champion Readings From World ECO `Watts & Co., London 14/B2 & Dorothy Short Religion 6 Bhupendra Datta Swami Vivekananda PER/BIO Nababharat Pub., 17/A3 Calcutta 7 H.D. Lewis The Principal Upanisads PHIL George Allen & Unwin 8/A1 14 Jawaherlal Nehru Buddhist Texts PHIL Bruno Cassirer 8/A1 15 Bhagwat Saran Women In Rgveda PHIL Nada Kishore & Bros., 8/A1 Benares. 15 Bhagwat Saran Upadhya Women in Rgveda LIT 9/B1 16 A.P. Karmarkar The Religions of India PHIL Mira Publishing Lonavla 8/A1 House 17 Shri Krishna Menon Atma-Darshan PHIL Sri Vidya Samiti 8/A1 Atmananda 20 Henri de Lubac S.J. Aspects of Budhism PHIL sheed & ward 8/A1 21 J.M. Sanyal The Shrimad Bhagabatam PHIL Dhirendra Nath Bose 8/A2 22 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam VolI 23 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vo.l III 24 J.M. Sanyal The Shrimad Bhagabatam PHIL Oriental Pub. 8/A2 25 J.M. Sanyal The Shrimad PHIL Oriental Pub. 8/A2 Bhagabatam Vol.V 26 Mahadev Desai The Gospel of Selfless G/REL Navijvan Press 14/B2 Action 28 Shankar Shankar's Children Art FIC/NOV Yamuna Shankar 2/A2 Number Volume 28 29 Nil The Adyar Library Bulletin LIT The Adyar Library and 9/B2 Research Centre 30 Fraser & Edwards Life And Teaching of PER/BIO Christian Literature 17/A3 Tukaram Society for India 40 Monier Williams Hinduism PHIL Susil Gupta (India) Ltd. -
The Mahabharata
^«/4 •m ^1 m^m^ The original of tiiis book is in tine Cornell University Library. There are no known copyright restrictions in the United States on the use of the text. http://www.archive.org/details/cu31924071123131 ) THE MAHABHARATA OF KlUSHNA-DWAIPAYANA VTASA TRANSLATED INTO ENGLISH PROSE. Published and distributed, chiefly gratis, BY PROTSP CHANDRA EOY. BHISHMA PARVA. CALCUTTA i BHiRATA PRESS. No, 1, Raja Gooroo Dass' Stbeet, Beadon Square, 1887. ( The righi of trmsMm is resem^. NOTICE. Having completed the Udyoga Parva I enter the Bhishma. The preparations being completed, the battle must begin. But how dan- gerous is the prospect ahead ? How many of those that were counted on the eve of the terrible conflict lived to see the overthrow of the great Knru captain ? To a KsJtatriya warrior, however, the fiercest in- cidents of battle, instead of being appalling, served only as tests of bravery that opened Heaven's gates to him. It was this belief that supported the most insignificant of combatants fighting on foot when they rushed against Bhishma, presenting their breasts to the celestial weapons shot by him, like insects rushing on a blazing fire. I am not a Kshatriya. The prespect of battle, therefore, cannot be unappalling or welcome to me. On the other hand, I frankly own that it is appall- ing. If I receive support, that support may encourage me. I am no Garuda that I would spurn the strength of number* when battling against difficulties. I am no Arjuna conscious of superhuman energy and aided by Kecava himself so that I may eHcounter any odds. -

ESSENCE of VAMANA PURANA Composed, Condensed And
ESSENCE OF VAMANA PURANA Composed, Condensed and Interpreted By V.D.N. Rao, Former General Manager, India Trade Promotion Organisation, Pragati Maidan, New Delhi, Union Ministry of Commerce, Govt. of India 1 ESSENCE OF VAMANA PURANA CONTENTS PAGE Invocation 3 Kapaali atones at Vaaranaasi for Brahma’s Pancha Mukha Hatya 3 Sati Devi’s self-sacrifice and destruction of Daksha Yagna (Nakshatras and Raashis in terms of Shiva’s body included) 4 Shiva Lingodbhava (Origin of Shiva Linga) and worship 6 Nara Narayana and Prahlada 7 Dharmopadesha to Daitya Sukeshi, his reformation, Surya’s action and reaction 9 Vishnu Puja on Shukla Ekadashi and Vishnu Panjara Stotra 14 Origin of Kurukshetra, King Kuru and Mahatmya of the Kshetra 15 Bali’s victory of Trilokas, Vamana’s Avatara and Bali’s charity of Three Feet (Stutis by Kashyapa, Aditi and Brahma & Virat Purusha Varnana) 17 Parvati’s weds Shiva, Devi Kaali transformed as Gauri & birth of Ganesha 24 Katyayani destroys Chanda-Munda, Raktabeeja and Shumbha-Nikumbha 28 Kartikeya’s birth and his killings of Taraka, Mahisha and Baanaasuras 30 Kedara Kshetra, Murasura Vadha, Shivaabhisheka and Oneness with Vishnu (Upadesha of Dwadasha Narayana Mantra included) 33 Andhakaasura’s obsession with Parvati and Prahlaad’s ‘Dharma Bodha’ 36 ‘Shivaaya Vishnu Rupaaya, Shiva Rupaaya Vishnavey’ 39 Andhakaasura’s extermination by Maha Deva and origin of Ashta Bhairavaas (Andhaka’s eulogies to Shiva and Gauri included) 40 Bhakta Prahlada’s Tirtha Yatras and legends related to the Tirthas 42 -Dundhu Daitya and Trivikrama -

Damayanti, De Víctima a Heroína O Una Prueba De Fidelidad
Káñina, Rev. Artes y Letras, Univ. Costa Rica XXXIX (1): 67-82, 2015 / ISSN: 2215-2636 DAMAYANTI, DE VÍCTIMA A HEROÍNA O UNA PRUEBA DE FIDELIDAD Damayanti, from victim to heroine or proof of loyalty Sol Argüello Scriba* RESUMEN Nala y Damayantī es una interpolación de la gran obra épica india el Mahābhārata, cuyo personaje principal es la heroína Damayantī. Sufre el destierro y los peligros de la selva inhóspita. Las descripciones de su belleza física muestran también su fortaleza espiritual y deberes de esposa, del suadharma, aspectos que la convierten en un modelo del estereotipo femenino de fidelidad en el Hinduismo. Palabras clave: estereotipo femenino, belleza, épica, literatura. ABSTRACT Nala and Damayantī is an interpolation of the great Indian epic Mahābhārata, whose main character is the heroine Damayantī.Suffers exile and the dangers of the inhospitable jungle. The descriptions of her physical beauty also show his spiritual strength and duties as a wife, the suadharma, aspects that makes her a feminine stereotype model of faithfulness in Hinduism. Key Words: feminine stereotype, beauty, epics, literature. * Universidad de Costa Rica, Profesor, Escuela de Filología, Lingüística y Literatura. Costa Rica Correo electrónico: [email protected] Recepción: 14/05/2014. Aceptación: 26/09/2014. 68 Káñina, Rev. Artes y Letras, Univ. Costa Rica XXXIX (1) (enero-junio): 67-82, 2015 / ISSN: 2215-2636 Introducción en la selva. Esa distinción por medio de las descripciones de ambos personajes, permiten Nala y Damayantī es una de la más distinguirlos de los otros personajes, los cuales conocidas narraciones interpoladas de amor, son apenas descritos, a excepción de los dioses sufrimiento, separación y encuentro del en el inicio de la obra. -

Dhruva Maharaj's Meeting with Nanda and Sunanda
Dhruva Maharaj’s meeting with Nanda and Sunanda Srimad Bhagavatam verse 4.12.22, (Class at Mayapur) Maharaj recites the verse: Tam Krishna-padabhinivishta chetasam Baddhanjalim prashraya namra kandharam Sunanda-nadau upasrutya sasmitam Pratyuchatuh pushkaranabha sammatau Translation: Dhruva Maharaj was always absorbed in thinking of the lotus feet of Lord Krishna. His heart was full with Krishna. When the two confidential servants of the Supreme Lord, who were named Nanda and Sunanda, approached him, smiling happily, Dhruva stood with folded hands, bowing humbly. They then addressed him as follows: Purport: Maharaj reads the purport by Srila Prabhupada: “In this verse, the wordpushkaranabha-sammatau is significant. Krishna, or Lord Vishnu, is known for His lotus eyes, lotus navel, lotus feet and lotus palms. Here, He is called pushkara-nabha, which means “the Supreme Personality of Godhead, who has a lotus navel,” andsammatau means “two confidential or very obedient servants.” The materialistic way of life differs from the spiritual way of life in that one is disobedience and the other is obedience to the will of the Supreme Lord. All living entities are part and parcel of the Supreme Lord, and they are supposed to be always agreeable to the order of the Supreme person; that is perfect oneness. In Vaikuntha world, all the living entities are in oneness with the Supreme Godhead because they never defy His orders. Here in the material world, however, they are not sammata, agreeable, but always asammata, disagreeable. This human form of life is a chance to be trained to be agreeable to the orders of the Supreme Lord. -

ADAPTED from KALIDASA's SANSKRIT EPIC Tfraghuvamsham
ADAPTED FROM KALIDASA'S SANSKRIT EPIC tfRAGHUVAMSHAM APPROVED BY THE COMICS AUTHORITY Tradition has it that Rama was the ideal king. Gandhiji was only reinforcing it when he named his ideal state ‘Rama-Rajya’. Yet the predecessors of Roma, in his dynasty of the Ikshwakus, were as valiant and as benign as Rama himself. This story tells of their deeds. The heroes of epics have their tragic flaws because epics always tell the whole truth. Like Rama, his ancestors also had flawed characters despite the glory of their per sonalities. Inspired by the epic of Valmiki, Kalidasa wrote his classic poem ‘Raghuvamsha’. While chronicling the lives of the ancestors of Rama, it noted the decline of the ruling house also. It is interesting to note that the Puranas trace the genealogy of Rama to the Sun. Some of the illustrious ancestors listed in the genealogy are Manu, Ikshwaku, Harischandra, Rohita, Sagara, Bhagiratha, Ambarisha and Rituparna. Brihadbala, who fought in the Mahabhorata war is said to be a descendant of Rama. WE HAVE BEEN COMPELLED TO INCREASE THE PRICE OF AMAR CHITRA KATHA TO RS. 2.50 PER COPY BECAUSE OF THE RISING COST OF PRODUCTION. WE REQUEST OUR READERS TO KINDLY BEAR WITH US. Published by H.G. Mirchandani for India Book House Education Trust, 29 Wodehouse Road, Bombay - 400 039 and printed by H.K.Nasta at IBH Printers,’ Marol Naka, Mathuradas Vissanji Road, Andheri (East), Bombay - 400 059*. Editor: Anant Pai Associate Editor: Kamala Chandrakant Script: Kaxnala Chandrakant Illustrations: Ram Waeerkar ANCESTORS OF RAMA RfMM ’5 ORtPiT-GRANDFATHER, THE PIOUS PILIPfl OF THE IK5HMKU M CE, M $ RENOWNED FOR Hie VIRTUE. -

Cradle Tales of Hinduism Bv the Same Author, Footfalls of Indian History
NY PUBLIC LIBRARY THE BRANCH LIBRARIES 3 3333 07251 1310 Digitized by the Internet Archive in 2007 with funding from IVIicrosoft Corporation http://www.archive.org/details/cradletalesofhinOOnive CRADLE TALES OF HINDUISM BV THE SAME AUTHOR, FOOTFALLS OF INDIAN HISTORY. With 6 Coloured Plates and 22 other Illustra- tions. Extra crown 8vo, "Js. 6d. net ; 2 R. 8 as. AN INDIAN STUDY OF LOVE AND DEATH. Crown Svo, 2s. 6d. net. THE MASTER AS I SAW HIM. Being Pages from the Life of the Swami Vivekananda. Crown 8vo, 5s. net. STUDIES FROM AN EASTERN HOME. With a Portrait, Prefatory Memoir by S. K. Ratcliffe, and Appreciations from Professor Patrick Geddes, Professor T. K. Cheyne, Mr. H. W. Nevinson, and Mr. Rabindranath Tagore. Crown 8vo, 3J, 6d. net ; i R. 4 as. RELIGION AND DHARMA. Crown 8vo, 3^^. net ; I R. 4 as. This is a book on the Religion of Hinduism, its aims, ideals, and meaning. It appeals especially to those who are students of native life and Religion in India, and particularly to those who have some knowledge of the new movements in thought, art, and religion which are arising among the Indian natives. LONGMANS, GREEN AND CO. BOMBAY, CALCUTTA, AND MADRAS LONDON AND NEW YORK The Indian Story Teller at NigKtfall CRADLE TALES OF HINDUISM BY THE SISTER NIVEDITA (MARGARET E. NOBLE) AUTHOR OF "the WEB OF INDIAN LIFE," ETC. WITH FRONTISPIECE NE'i^r IMPRESSION LONGMANS, GREEN AND CO. HORNBY ROAD, BOMBAY 6 OLD COURT HOUSE STREET, CALCUTTA 167 MOUNT ROAD, MADRAS LONDON AND NEW YORK 1917 All rights reserved v) THE NEW YORK PUBLIC LIRHARY ASTw^, L6NOX AN» T<LDeN FOUNDaTIONI. -

Dr. Babasaheb Ambedkar Writings & Speeches Vol. 4
Babasaheb Dr. B.R. Ambedkar (14th April 1891 - 6th December 1956) BLANK DR. BABASAHEB AMBEDKAR WRITINGS AND SPEECHES VOL. 4 Compiled by VASANT MOON Dr. Babasaheb Ambedkar : Writings and Speeches Vol. 4 First Edition by Education Department, Govt. of Maharashtra : October 1987 Re-printed by Dr. Ambedkar Foundation : January, 2014 ISBN (Set) : 978-93-5109-064-9 Courtesy : Monogram used on the Cover page is taken from Babasaheb Dr. Ambedkar’s Letterhead. © Secretary Education Department Government of Maharashtra Price : One Set of 1 to 17 Volumes (20 Books) : Rs. 3000/- Publisher: Dr. Ambedkar Foundation Ministry of Social Justice & Empowerment, Govt. of India 15, Janpath, New Delhi - 110 001 Phone : 011-23357625, 23320571, 23320589 Fax : 011-23320582 Website : www.ambedkarfoundation.nic.in The Education Department Government of Maharashtra, Bombay-400032 for Dr. Babasaheb Ambedkar Source Material Publication Committee Printer M/s. Tan Prints India Pvt. Ltd., N. H. 10, Village-Rohad, Distt. Jhajjar, Haryana Minister for Social Justice and Empowerment & Chairperson, Dr. Ambedkar Foundation Kumari Selja MESSAGE Babasaheb Dr. B.R. Ambedkar, the Chief Architect of Indian Constitution was a scholar par excellence, a philosopher, a visionary, an emancipator and a true nationalist. He led a number of social movements to secure human rights to the oppressed and depressed sections of the society. He stands as a symbol of struggle for social justice. The Government of Maharashtra has done a highly commendable work of publication of volumes of unpublished works of Dr. Ambedkar, which have brought out his ideology and philosophy before the Nation and the world. In pursuance of the recommendations of the Centenary Celebrations Committee of Dr. -

States of Affect: Trauma in Partition/Post-Partition South Asia
STATES OF AFFECT: TRAUMA IN PARTITION/POST-PARTITION SOUTH ASIA By Rituparna Mitra A DISSERTATION Submitted to Michigan State University in partial fulfillment of the requirements for the degree of English – Doctor of Philosophy 2015 ABSTRACT STATES OF AFFECT: TRAUMA IN PARTITION/POST-PARTITION SOUTH ASIA By Rituparna Mitra The Partition of the Indian subcontinent – into India and Pakistan in 1947 – was one of the crucial moments marking the break between the colonial and postcolonial era. My project is invested in exploring the Partition not merely in terms of the events of August 1947, but as an ongoing process that continues to splinter political, cultural, emotional and sexual life-worlds in South Asia. My dissertation seeks to map analytical pathways to locate the Partition and the attendant formations of minoritization and sectarian violence as continuing, unfolding processes that constitute postcolonial nation-building. It examines the far-reaching presence of these formations in current configurations of politics, culture and subjectivity by mobilizing the interdisciplinary scope of affect-mediated Trauma and Memory Studies and Postcolonial Studies, in conjunction with literary analysis. My project draws on a wide range of cultural artifacts such as poetry, cantillatory performance, mourning rituals, testimonials, archaeological ruins, short stories and novels to develop a heuristic and affective re-organization of post-Partition South Asia. It seeks to illuminate through frameworks of memory, melancholia, trauma, affect and postcoloniality how the ongoing effects of the past shape the present, which in turn, offers us ways to reimagine the future. This dissertation reaches out to recent work developing a vernacular framework to analyze violence, trauma and loss in South Asia. -

Rajaji-Mahabharata.Pdf
MAHABHARATA retold by C. Rajagopalachari (Edited by Jay Mazo, International Gita Society) Contents 39. The Wicked Are Never Satisfied 1. Ganapati, the Scribe 40. Duryodhana Disgraced 2. Devavrata 41. Sri Krishna's Hunger 3. Bhishma's Vow 42. The Enchanted Pool 4. Amba And Bhishma 43. Domestic Service 5. Devayani And Kacha 44. Virtue Vindicated 6. The Marriage Of Devayani 45. Matsya Defended 7. Yayati 46. Prince Uttara 8. Vidura 47. Promise Fulfilled 9. Kunti Devi 48. Virata's Delusion 10. Death Of Pandu 49. Taking Counsel 11. Bhima 50. Arjuna's Charioteer 12. Karna 51. Salya Against His Nephews 13. Drona 52. Vritra 14. The Wax Palace 53. Nahusha 15. The Escape Of The Pandavas 54. Sanjaya's Mission 16. The Slaying Of Bakasura 55. Not a Needle-Point Of Territory 17. Draupadi's Swayamvaram 56. Krishna's Mission 18. Indraprastha 57. Attachment and Duty 19. The Saranga Birds 58. The Pandava Generalissimo 20. Jarasandha 59. Balarama 21. The Slaying Of Jarasandha 60. Rukmini 22. The First Honor 61. Non-Cooperation 23. Sakuni Comes In 62. Krishna Teaches 24. The Invitation 63. Yudhishthira Seeks Benediction 25. The Wager 64. The First Day's Battle 26. Draupadi's Grief 65. The Second Day 27. Dhritarashtra's Anxiety 66. The Third Day's Battle 28. Krishna's Vow 67. The Fourth Day 29. Pasupata 68. The Fifth Day 30. Affliction Is Nothing New 69. The Sixth Day 31. Agastya 70. The Seventh Day 32. Rishyasringa 71. The Eighth Day 33. Fruitless Penance 72. The Ninth Day 34. Yavakrida's End 73. -

Analysis of Hindu Widowhood in Indian Literature Dipti Mayee Sahoo
IOSR Journal Of Humanities And Social Science (IOSR-JHSS) Volume 21, Issue 9, Ver. 7 (Sep. 2016) PP 64-71 e-ISSN: 2279-0837, p-ISSN: 2279-0845. www.iosrjournals.org Analysis Of Hindu Widowhood In Indian Literature Dipti Mayee Sahoo Asst. Prof. SociologyTrident Academy of Creative technology,Bhubaneswar Abstract:- In ancient India, women occupied a very important position, in fact a superior position to, men. It is a culture whose only words for strength and power are feminine -"Shakti'' means "power'' and "strength.'' All male power comes from the feminine. Literary evidence suggests that kings and towns were destroyed because a single woman was wronged by the state. For example, Valmiki's Ramayana teaches us that Ravana and his entire clan was wiped out because he abducted Sita. Veda Vyasa'sMahabharatha teaches us that all the Kauravas were killed because they humiliated Draupadi in public. ElangoAdigal'sSillapathigaram teaches us Madurai, the capital of the Pandyas was burnt because PandyanNedunchezhiyan mistakenly killed her husband on theft charges. "In Hinduism, the momentous event of a foundation at one point in time, the initial splash in the water, from which concentric circles expand to cover an ever-wider part of the total surface, is absent. The waves that carried Hinduism to a great many shores are not connected to a central historical fact or to a common historic movement. " Key words:- Feminine, sakti, strength, humiliation, power. I. INTRODUCTION In this age of ascending feminism and focus on equality and human rights, it is difficult to assimilate the Hindu practice of sati, the burning to death of a widow on her husband's funeral pyre, into our modern world. -

(Based on Kashi Khand and Ling Puraan) Lalitha V
SHIV LINGS OF KASHI (BASED ON KASHI KHAND AND LING PURAAN) LALITHA V. ABOUT THE AUTHOR The Author, Lalitha. V. is the daughter of Late Smt. Kaveri Narayan and Late A.S. Narayan of Unnat Nagar-II, Goregaon (W), Mumbai. Late A.S. Narayan was one of the founder members of Vivek Vidyalaya, Goregaon (W). Lalitha. V. is the daughter-in-law of Late Jagadhambal, a staunch devotee and Late P.K. Sivasubramanian of Sri Ram Nagar, Andheri, Mumbai, who shifted to Kashi in 1978. She is the wife of Shri P.S. Venkataramanan, of SBI, based in Varanasi. Lalitha V. is a staunch devotee and she, alongwith her husband and several family friends, visited over 350 temples in Kashi and brought out several books on that subject. She has written the following books : 1. Temples of Kashi. 2. Kashi Ke Devalay (in Hindi) 3. Saundarya Lahari (Translation and explanation) 4. Lalitha Sahasranamam (Translation and explanation) 5. Vishnu Sahasranamam (Translation and explanation) 6. Kashiyil Kovilgal (Kashi Kaandam) in Tamil 7. Graha Dosham and Pariharam (in Kashi & Tamil Nadu) 8. Kashiteel Shiv Lingey (Marathi) 9. Simple Remedies for Planetary Afflictions 10.Kashiyil Shiva Lingangal (Malayalam) She also proposes to write extensively on spirituality and bring out books in paperback form as well as ebook form. She is thankful to all the well- wishers who helped her in the holy task. (LALITHA. V.) G-1, Block-1, Varuna Enclave, S-2/636, Club Road, Secrole, Varanasi-221 002. 9839061178 (Whatsapp only) SPECIAL CONTRIBUTION BY LATE JAGADHAMBAL The Author deems it necessary to highlight the special contribution made by Late Jagadhambal (to whom this book has been dedicated) with respect to Kashi Khand.