DOCSLIB.ORG

The Maximum Diversity Assortment Selection Problem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Maximum Diversity Assortment Selection Problem Takustr. 7 Zuse Institute Berlin 14195 Berlin Germany FELIX PRAUSE1,KAI HOPPMANN-BAUM2,BORIS DEFOURNY3,THORSTEN KOCH4 The Maximum Diversity Assortment Selection Problem 1 0000-0001-9401-3707 2 0000-0001-9184-8215 3 0000-0003-0405-5538 4 0000-0002-1967-0077 ZIB Report 20-34 (Dezember 2020) Zuse Institute Berlin Takustr. 7 14195 Berlin Germany Telephone: +49 30-84185-0 Telefax: +49 30-84185-125 E-mail: [email protected] URL: http://www.zib.de ZIB-Report (Print) ISSN 1438-0064 ZIB-Report (Internet) ISSN 2192-7782 The Maximum Diversity Assortment Selection Problem Felix Prause1[0000−0001−9401−3707], Kai Hoppmann-Baum1;2[0000−0001−9184−8215], Boris Defourny3[0000−0003−0405−5538], and Thorsten Koch1;2[0000−0002−1967−0077] 1 Zuse Institute Berlin, Takustr. 7, 14195 Berlin, Germany {prause,hoppmann-baum,koch}@zib.de 2 TU Berlin, Chair of Software and Algorithms for Discrete Optimization, Str. des 17. Juni 135, 10623 Berlin, Germany 3 Lehigh University, Department of Industrial and Systems Engineering, 200 W Packer Ave, Bethlehem, PA, 18015, USA [email protected] Abstract. In this paper, we introduce the Maximum Diversity Assort- ment Selection Problem (MADASS), which is a generalization of the 2-dimensional Cutting Stock Problem (2CSP). Given a set of rectan- gles and a rectangular container, the goal of 2CSP is to determine a subset of rectangles that can be placed in the container without overlap- ping, i.e., a feasible assortment, such that a maximum area is covered. In MADASS, we need to determine a set of feasible assortments, each of them covering a certain minimum threshold of the container, such that the diversity among them is maximized. Thereby, diversity is defined as minimum or average normalized Hamming-Distance of all assortment pairs. The MADASS Problem was used in the 11th AIMMS-MOPTA Competition in 2019. The methods we describe in this article and the computational results won the contest. In the following, we give a def- inition of the problem, introduce a mathematical model and solution approaches, determine upper bounds on the diversity, and conclude with computational experiments conducted on test instances derived from the 2CSP literature. 1 Introduction The problem of packing rectangles into rectangular containers or to cut them from rectangular stock sheets arises in a variety of industrial operations. Thereby, one typically aims at determining a feasible solution where the wasted material or space is minimized. Consider for example the paper, glass, wood, textile, or metal industry. Here, rectangular pieces are needed for the production of certain goods, which are typically cut from given stock pieces [43]. Another common application arising in logistics is to load pallets or containers [49]. Furthermore, similar problems appear in the production and operation of microchips, namely 2 Prause et al. in the layout of processor chips [77] and the dynamic allocation of memory as well as in multiprocessor scheduling [43]. Finally, the editing and lay-outing of newspapers [76] or the arrangement of products on supermarket shelves [2] belong to this class of applications, too. These problems are typically modeled as some special variant of the 2-dim Cutting Stock Problem (2CSP), which we introduce in Section 2 and discuss in Section 3. However, for practitioners it is often useful when they are presented not only one optimal but a set of diverse “near-optimal” solutions from which she or he can choose. This holds especially for those tasks where it is hard to formalize or model important side constraints. Consider, for example, the last two exam- ples from above. If a supermarket wants to investigate the buying behavior of its customers, an arrangement of the products minimizing the empty space is certainly desirable. Nevertheless, for this particular task the result is not very meaningful. Instead, the company needs to conduct tests with a variety of ar- rangements to assess whether they increase the purchasing rates [52]. Similarly, when it comes to the layout of texts, pictures, or ads on a newspaper page, the result does not necessarily have to be minimal w.r.t. the resulting empty space, but has to come in some aesthetic appeal. Thus, presenting the user with a se- lection of assortments that cover some minimum threshold of the available area can be advantageous in all areas where experiences and subjective perceptions of humans have an impact on the chosen solution. Problems of this kind are the motivation for the Maximum Diversity As- sortment Selection Problem (MADASS), which we introduce in Section 2. We review the literature on two inherent subproblems in Section 3: the above men- tioned 2CSP and the Maximum Diversity Problem (MDP), where a predefined number of elements has to be selected from a given set such that the diversity among them is maximized. Before discussing an MIQP model for MADASS in Section 5, we introduce MIQP formulations to determine upper bounds on the maximum diversity in Section 4. Next, we present a generic two-stage heuris- tic in Section 6. We present extensive computational experiments in Section 7. Finally, we conclude and give an outlook on future research in Section 8. 2 Definitions and Problem Setup In MADASS, we are given a rectangle C with width w 2 Z≥0 and height h 2 Z≥0, which we call container. Furthermore, we are given a set of rectangles R := fR1; :::; Rng and each of them is associated with its width wi 2 Z≥0 and its height hi 2 Z≥0. Next, an assortment is a subset A ⊆ R of rectangles, i.e., A 2 P(R) where P(R) denotes the powerset of R. We call an assortment A feasible if it can be placed in the container C without overlapping, i.e., if we can 2 assign a bottom-left corner coordinate (xi; yi) 2 R to each rectangle Ri 2 A such that [xi; xi + wi) × [yi; yi + hi) ⊆ [0; w) × [0; h) and for all Ri;Rj 2 A with i 6= j we have [xi; xi + wi)×[yi; yi + hi)\[xj; xj + wj)×[yj; yj + hj) = ;. In the sequel, we denote the set of all feasible assortments by F. Next, each assortment A has an associated value v(A) = P w h , which is the sum of the areas of Ri2A i i The Maximum Diversity Assortment Selection Problem 3 the rectangles it contains. We call an assortment A∗ optimal if it is feasible and if v(A∗) ≥ v(A) holds for every A 2 F. Determining an optimal assortment is called the 2-dimensional Cutting Stock Problem (2CSP). Note that we otherwise allow an arbitrary placement of the rectangles inside the container, i.e., we do not impose any further conditions, and we do not allow the rotation of rectangles. An example can be found in Figure 1. R2 h2 R3 h3 R1 h1 w2 w3 h w1 R5 h5 R4 h4 w4 w5 C w R R4 R4 R4 R3 R5 R5 R1 R1 R1 R1 R2 R2 R2 C C C C A1 A2 A3 A4 Fig. 1: Container C with rectangle set R. While assortment A1 is feasible, A2 is even optimal. On the other hand, assortments A3 and A4 are not feasible. In MADASS we are furthermore given a threshold value v 2 [0; v(C)], with v(C) := wh denoting the area of the container, as well as a natural number m 2 N with m ≥ 2. We call an assortment A v-good if it is feasible and if v(A) ≥ v and we denote the set of v-good assortments by Fv ⊆ F. Furthermore, a selection is a multi-subset S ⊆ P(R) of assortments of cardinality jSj = m, i.e., we allow that an assortment is contained more than once in S. We call S feasible if all of its assortments are v-good, i.e., if S ⊆ Fv. Additionally, we are given a diversity function δ for selections and call δ(S) the diversity of selection S. The two diversity functions that we consider in this paper are based on the Hamming-Distances between assortment pairs contained in S and are discussed in Subsection 2.1. Finally, a selection S∗ is called optimal if it is feasible and if δ(S∗) ≥ δ(S) holds for all feasible selections S. In the following, we denote a MADASS instance I as quintuple I := (C; R; m; v; δ). Lemma 1. MADASS is NP-hard. 4 Prause et al. Proof. We prove this by reduction from 2CSP, which is NP-hard, see Fekete and Schepers [29] and Garey and Johnson [32]. Given an instance of 2CSP with container C and set of rectangles R, for arbitrary m and δ, there exists a feasible assortment of value at least v if and only if there exists a feasible selection for MADASS instance I := (C; R; m; v; δ). 2.1 Diversity of Selections A common distance measure applied to the subsets of a common superset is the Hamming-Distance [41]. Given an assortment A, we associate the vector n i vA 2 f0; 1g with it, where the i-th entry vA is equal to 1 if rectangle Ri is contained in A and 0 otherwise. For two assortments A and A0, the (normalized) Hamming-Distance is n P i i jvA − vA0 j d (A; A0) := i=1 : H jAj + jA0j 0 0 Furthermore, we set dH (A; A ) = 0 in the case A = A = ;. Note that we consider the normalized Hamming-Distance, i.e., we divide by jAj + jA0j, to ensure that the number of rectangles forming the assortments has no impact on the distance.
Load more

Recommended publications
  • The Structure of Poly (Da): Poly (Dt) in a Condensed State and in Solution
    volume 15 Number 14 1987 Nucleic Acids Research The structure of poly(dA): poly(dT) in a condensed state and in solution A.A.Lipanov1 and V.P.Chuprina* Research Computer Center, USSR Academy of Sciences, Pushchino, Moscow Region and 'Institute of Molecular Genetics, USSR Academy of Sciences, Moscow, USSR Received April 3, 1987; Revised June 16, 1987; Accepted June 25, 1987 •V ABSTRACT New X-ray and energetically optimal models of poly(dA):poly(dT) with ^ the hydration spine in the minor groove have been compared with the NMR data in solution (Behling, R.W. and Kearns, D.R. (1986) Biochemistry ^5, 3335-3346). These models have been refined to achieve a better fit with the * NMR data. The obtained results suggest that the poly(dA):poly(dT) structure ^v in a condensed state is similar to that in solution. The proposed conforma- tions of poly(dA):poly(dT), unlike the classic B form, satisfy virtually «.v all geometrical requirements which follow from the NMR data. Thus, the X-ray and energetically optimal poly(dA):poly(dT) structures (or those with slight ^ modifications) can be considered as credible models of the poly(dA):poly(dT) double helix in solution. One of the features distinguishing these models from the classic B form is a narrowed minor groove. • INTRODUCTION "*• The poly(dA) :poly(dT) structure has been extensively discussed lately. >-A One of the reasons of such an increased interest is the observation that some natural DMAs display bending which has been attributed to structural A features of dA :dT runs (ref.
    [Show full text]
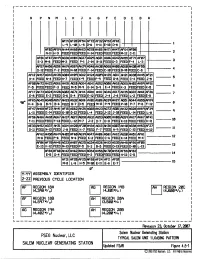
  • Salem Generating Station, Units 1 & 2, Revision 29 to Updated Final Safety Analysis Report, Chapter 4, Figures 4.5-1 to 4.5
    r------------------------------------------- 1 I p M J B I R N L K H G F E D c A I I I I I Af'Jq AF20 AF54 AF72 32 AF52 AF18 I L-q L-10 L-15 D-6 -11 E-10 D-8 l I AF03 Af't;qAH44 AH60 AH63 AG70 AH65 AH7l AH47 AFS4 AF08 I N-ll H-3 FEED FEED FEED H-14 FEED FEED FEED M-12 C-11 2 I AF67 AH4q AH04 AG27 AG2<i' AG21 AG16 AG42 AF71 AF07 AF01 AG36 AH!5!5 3 I E-3 M-6 FEED M-3 FEED P-1 J-14 B-11 FEED D-3 FEED F-4 L-3 I AF67 AH5S AG56 Atflq AGsq AH2<1' AG48 AH30 AG68 AH08 AG60 AH30 AF55 I D-12 FEED F-2 FEED N-11 FEED F-14 FEED C-11 FEED B-11 FEED C-8 4 I AF12 AH57 AG43 AH38 AHtiJq AG12 AH24 AGfR AH25 AGil AG31 AH45 AF21 AGlM AH21 5 I H~4 FEED N-4 FEED H-7 FEED K~q FEED F-q FEED G-8 FEED C-4 FEED J-15 I AF50 AH72 AH22 AGS6 AH15 AGll.lAG64 AG41 AG52 AG88 AH18 AG65 AHIJ2 AH5q AF51 I F-5 FEED FEED F-3 FEED M-5 r+q G-14 o-q E-4 FEED K-3 FEED FEED K-5 6 I f:Fl7 AH73 AG24 AH28 AG82 AG71 AH14 AG18 AHil AG46 AG17 AH35 AG22 AH61 AF26 7 I E-8 FEED E-2 FEED G-6 G-4 FEED E-12 FEED J-4 J-6 FEED L-2 FEED E-5 I Af&q I qeo AF65 AG45 AtM0 AG57 AH33 AG32 AG16 AH01 AGI6 AG3<1' AH27 AG51 AG44 AG55 K-4 B-8 e-q B-6 FEED B-7 P-5 FEEC M-11 P-q FEED P-11 P-7 P-8 F-12 8 I AF47 AH68 AF23 AH41 AF1!5 AG62 AH26 AG03 AH23 AH32 AG28 AHsq AF3<1' q I L-U FEED E-14 FEED G-10 G-12 FEED L-4 FEED FEED L-14 FEED L-8 I ~~ AF66 AH66 AH10 AG67 AH37 AGJq AG68 AG3l AG63 AG05 AH08 AG5q AH17 AH67 AF41 I F-11 FEED FEED F-13 FEED L-12 M-7 J-2 D-7 D-11 FEED K-13 FEED FEED K-11 10 I AE33 AH!52 AG37 AH31 AG14 AH20 AF20 AH34 AG13 AH36 AG07 AH40 AG38 AH!53 AF27 I G-ll FEED N-12 FEED J-8 FEED K-7 FEED
    [Show full text]
  • Policy & Governance Committee
    AGENDA BOG Policy & Governance Committee Meeting Date: February 12, 2021 Location: Videoconference Chair: Kamron Graham Vice-Chair: Kate Denning Members: Gabriel Chase, Kate Denning, John Grant, Rob Milesnick, Curtis Peterson, Joe Piucci, David Rosen Staff Liaison: Helen M. Hierschbiel Charge: Develops and monitors the governing rules and policies relating to the structure and organization of the bar; ensures that all bar programs and services comply with organizational mandates and achieve desired outcomes. Identifies and brings emerging issues to the BOG for discussion and action. 2021 PGC Work Plan 1. Wellness Task Force Report. Review report and decide whether to pursue any Exhibit Action 10 recommendations. 2. Evidence-Based Decision-Making Policy. Review Futures Task Force recommendation regarding evidence-based decision-making To Be Posted Action 10 policy and consider whether to adopt the recommended policy. 3. HOD Authority. Discuss whether to pursue changes to limits of HOD authority either Exhibit Action 10 through amendments to HOD Rules or Bar Act. 4. OSB Bylaw Overhaul. Review draft of OSB bylaw overhaul, splitting between policies and Exhibit Discussion 20 bylaws. 5. Bar Sponsorship of Lawyer Referral Services. Review issue presented by Legal Ethics Exhibit Discussion 20 Committee. February 12, 2021 Policy & Governance Committee Agenda Page 2 6. Section Program Review. Review feedback Exhibit Discussion 20 regarding proposed changes to bylaws. 7. Approve minutes of January 8, 2021 meeting. Exhibit Action 1 2021 POLICY & GOVERNANCE WORK PLAN February 12, 2021 draft 2021 AREAS OF TO DO TASKS IN PROCESS (PGC) PGC TASKS DONE IN PROCESS (BOG) BOG TASKS FOCUS 1. Identify information needed 1.
    [Show full text]
  • Asia-Europe Connectivity Vision 2025
    Asia–Europe Connectivity Vision 2025 Challenges and Opportunities The Asia–Europe Meeting (ASEM) enters into its third decade with commitments for a renewed and deepened engagement between Asia and Europe. After 20 years, and with tremendous global and regional changes behind it, there is a consensus that ASEM must bring out a new road map of Asia–Europe connectivity and cooperation. It is commonly understood that improved connectivity and increased cooperation between Europe and Asia require plans that are both sustainable and that can be upscaled. Asia–Europe Connectivity Vision 2025: Challenges and Opportunities, a joint work of ERIA and the Government of Mongolia for the 11th ASEM Summit 2016 in Ulaanbaatar, provides the ideas for an ASEM connectivity road map for the next decade which can give ASEM a unity of purpose comparable to, if not more advanced than, the integration and cooperation efforts in other regional groups. ASEM has the platform to create a connectivity blueprint for Asia and Europe. This ASEM Connectivity Vision Document provides the template for this blueprint. About ERIA The Economic Research Institute for ASEAN and East Asia (ERIA) was established at the Third East Asia Summit (EAS) in Singapore on 21 November 2007. It is an international organisation providing research and policy support to the East Asia region, and the ASEAN and EAS summit process. The 16 member countries of EAS—Brunei Darussalam, Cambodia, Indonesia, Lao PDR, Malaysia, Myanmar, Philippines, Singapore, Thailand, Viet Nam, Australia, China, India, Japan, Republic of Korea, and New Zealand—are members of ERIA. Anita Prakash is the Director General of Policy Department at ERIA.
    [Show full text]
  • Oneida County Legislative District 1 Date: April 1, 2014
    CARTER RD D D 5 R R 6 B T 3 L L I E P L P S A T K E U C E T 5 C 6 K R D D U W O 3 M R W O D E O R S E R A K T R L Y T N C E E A A S E U D H G R I C Y T O I E O E D E R ID R A R A T R N N R F D C R D E W E O R N S E G S N D R H R E T D T E E S E A L D H S E E R I R T O S T U R I 10 D R M S N W I S R A G E A C N L H R T Y Verona D R AC11 AC12 AC13 AC14 AC15 E AC16 AC17 AC18 H AC19 R C R W H T L D R E I IL D L D D R L S E VERONA 4 R E B R M U N L R D I E T A K C K H A C O O U R S 6 R TA R N D TE 2 D R T OU R LO TE W E 31 Y EL T L U D R D R D O E R R L L B N R O E S T G E N T W E D I B A R L T O D S R NS E D T A D S A M M R R R T H 4 WESTMORELAND 3 R E C E N R RO A E N R E U FR TE N D U G Y T H B R 31 D D R S I I L D E R Y 5 YD R L R 6 L BO R D 5 L R N 3 I I 6 E SPR R H A 3 ING RD M M G E D S 3 R M E L I E T O E W N U T R EL I F U L I O RD E S L R O PR I-90 R D R ING STAT D E RD I- E R T E 90 OU T T A D AD11 AD12 AD13 E AD14 T A AD15 AD16 AD17 AD18 AD19 31 S T R S I-90 I-90 H 0 T I-9 L I OW D E R M S LL S PR VERONA 3 L ING H RD IL 0 OUS H I-90 I-9 E RD FOSTE D R CORN N ERS RD A T S S N D I R A E I-90 R M O Y I-90 O IL DA 5 M D D R 36 I-90 I-90 R E S A T -90 MIT G I C HEL S E U L R WN L R D O I O D T NE N R I D R I-90 I R RD S K SK KINNE R N 0 E N T RD -9 T 5 E I I E 0 L A 6 R L 9 S A J I- P 3 D D T T S R WESTMORELAND 4 D S E Y R E A LL R E W T N E C NL D T H O O E U H C L T F I R O R I L L M E O I R O L L X M W U D IL HIL E L T R R O M 0 T I-9 A E D E O R IN AE11 AE12 AE1R 3 T AE14 D AE15 AE16 L AE17 AE18 AE19 R D S R 3 N C D 1 E EN OW TE
    [Show full text]
  • Purification and Partial Characterization of a Coagulant Tle
    Received: September 4, 2008 J Venom Anim Toxins incl Trop Dis. Accepted: February 13, 2009 V.15, n.3, p.411-423, 2009. Abstract published online: March 5, 2009 Original paper. Full paper published online: August 31, 2009 ISSN 1678-9199. PURIFICATION AND PARTIAL CHARACTERIZATION OF A COAGULANT SERINE PROTEASE FROM THE VENOM OF THE IRANIAN SNAKE Agkistrodon halys Ghorbanpur M (1), Zare Mirakabadi A (2), Zokaee F (1), Zolfagarrian H (2), Rabiei H (2) (1) Chemical Engineering Department, Amirkabir University, Tehran, Iran; (2) Department of Venomous Animals and Antivenom Production, Razi Vaccine and Serum Research Institute, Karaj, Iran. ABSTRACT: Agkistrodon halys is one of several dangerous snake species in Iran. Among the most important signs and symptoms in patients envenomated by this snake is disseminated intravascular coagulation. A thrombin-like enzyme, called AH143, was isolated from Agkistrodon halys venom by gel filtration on a Sephadex G-50 column, ion-exchange chromatography on a DEAE-Sepharose and high performance liquid chromatography (HPLC) on a C18 column. In the final stage of purification, 0.82 mg of purified enzyme was obtained from 182.5 mg of venom. The purified enzyme showed a single protein band by sodium dodecyl sulfate polyacrylamide gel electrophoresis (SDS-PAGE), under reducing conditions, and its molecular mass was found to be about 30 kDa. AH143 revealed clotting activity in human plasma, which was not inhibited by EDTA or heparin. This enzyme still demonstrated coagulation activity when exposed to variations in temperature and pH ranging, respectively, from 30 to 40°C and from 7.0 to 8.0.
    [Show full text]
  • Radiation, Protection of the Public and the Environment (Poster Session 1) Origin and Migration of Cs-137 in Jordanian Soils
    Major scientific thematic areas: TA6 – Radiation, Protection of the Public and the Environment (Poster session 1) Origin and Migration of Cs-137 in Jordanian Soils Ahmed Qwasmeh, Helmut W. Fischer IUP- Institute for Environmental Physics, Bremen University, Germany Abstract Whilst some research and publication has been done and published about natural radioactivity in Jordan, only one paper has been published about artificial radioactivity in Jordanian soils (Al Hamarneh 2003). It reveals high concentrations of 137Cs and 90Sr in some regions in the northwest section of Jordan. The origin of this contamination was not determined. Two sets of soil samples were collected and brought from northwest section of Jordan for two reasons, namely; the comparable high concentration of 137Cs in this region according to the above-mentioned paper and because most of the population concentrates in this region. The first set of samples was collected in April 2004 from eleven different sites of this region of Jordan. The second set of samples has been brought in July 2005 from six of the previous sites where we had found higher 137Cs contamination. The second set was collected as thinner sliced soil samples for further studying and to apply a suitable model for 137Cs migration in soil. Activity of 137Cs was measured using a HpGe detector of 50% relative efficiency and having resolution of 2keV at 1.33MeV. Activity of 90Sr was measured for the samples of four sites of the first set of samples, using a gas-filled proportional detector with efficiency of 21.3% cps/Bq. The total inventory of 137Cs in Bq/m2 has been calculated and the correlation between 137Cs inventory and annual rainfall and site Altitude has been studied.
    [Show full text]
  • 1St IRF Asia Regional Congress & Exhibition
    1st IRF Asia Regional Congress & Exhibition Bali, Indonesia November 17–19 , 2014 For Professionals. By Professionals. "Building the Trans-Asia Highway" Bali’s Mandara toll road Executive Summary International Road Federation Better Roads. Better World. 1 International Road Federation | Washington, D.C. ogether with the Ministry of Public Works Indonesia, we chose the theme “Building the Trans-Asia Highway” to bring new emphasis to a visionary project Tthat traces its roots back to 1959. This Congress brought the region’s stakeholders together to identify new and innovative resources to bridge the current financing gap, while also sharing case studies, best practices and new technologies that can all contribute to making the Trans-Asia Highway a reality. This Congress was a direct result of the IRF’s strategic vision to become the world’s leading industry knowledge platform to help countries everywhere progress towards safer, cleaner, more resilient and better connected transportation systems. The Congress was also a reflection of Indonesia’s rising global stature. Already the largest economy in Southeast Asia, Indonesia aims to be one of world’s leading economies, an achievement that will require the continued development of not just its own transportation network, but also that of its neighbors. Thank you for joining us in Bali for this landmark regional event. H.E. Eng. Abdullah A. Al-Mogbel IRF Chairman Minister of Transport, Kingdom of Saudi Arabia Indonesia Hosts the Region’s Premier Transportation Meeting Indonesia was the proud host to the 1st IRF Asia Regional Congress & Exhibition, a regional gathering of more than 700 transportation professionals from 52 countries — including Ministers, senior national and local government officials, academics, civil society organizations and industry leaders.
    [Show full text]
  • BELLA COOLA to FOUR MILE TRAIL
    BELLA COOLA to FOUR MILE TRAIL Trail Location & Engineering Design Project sponsored by Bella Coola General Hospital Central Coast Regional District & Union of BC Municipalities December 14, 2009 PO Box 216, Hagensborg, BC V0T 1H0 Tel:250-982-2515, [email protected] BC-4Mile Trail Layout Report -i- TABLE OF CONTENTS 1 INTRODUCTION 1 1.1 Layout & Survey Method 1 1.2 Trail Design Criteria 1 2 TRAIL LAYOUT & DESCRIPTION 1 2.1 Cut and Fill 2 2.2 Partial Fill 2 2.3 Overland Fill 3 2.4 Flush Surfacing 3 2.5 Detailed Description 4 2.6 Tatsquan Creek Crossing Options 5 2.6.1 Option A - Hwy 20 Sidewalk 5 2.6.2 Option A2 – Widened Sidewalk on Hwy Bridge 5 2.6.3 Option B – Parallel Footbridge 6 2.6.4 Option C – Downstream Footbridge 7 3 ENVIRONMENT 8 3.1 Fish 8 3.2 Wildlife 8 4 FIELD REVIEW 9 5 CONSTRUCTION 9 5.1 Trail Components 11 5.1.1 Asphalt 11 5.1.2 Crush Gravel 11 5.1.3 Sub-grade Ballast 11 5.1.4 Foot Bridges 11 5.1.5 Culverts 11 5.1.6 Benches 12 5.1.7 Guards 12 5.1.8 Trail Posts 12 5.2 Next Engineering Steps 12 6 TRAIL MAINTENANCE 12 BC-4Mile Trail Layout Report -ii- APPENDIX A – AIRPHOTO MAP OF TRAIL 13 APPENDIX B – SURVEY MAP OF TRAIL 13 APPENDIX C – ENGINEERED PLAN, PROFILE & CROSS SECTIONS 13 Acknowledgement A number of individuals contributed time and knowledge to this initial stage of locating the proposed trail and Frontier Resource Management Ltd is very grateful for this help.
    [Show full text]
  • Asian Highway Handbook United Nations
    ECONOMIC AND SOCIAL COMMISSION FOR ASIA AND THE PACIFIC ASIAN HIGHWAY HANDBOOK UNITED NATIONS New York, 2003 ST/ESCAP/2303 The Asian Highway Handbook was prepared under the direction of the Transport and Tourism Division of the United Nations Economic and Social Commission for Asia and the Pacific. The team of staff members of the Transport and Tourism Division who prepared the Handbook comprised: Fuyo Jenny Yamamoto, Tetsuo Miyairi, Madan B. Regmi, John R. Moon and Barry Cable. Inputs for the tourism- related parts were provided by an external consultant: Imtiaz Muqbil. The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. This publication has been issued without formal editing. CONTENTS I. INTRODUCTION TO THE ASIAN HIGHWAY………………. 1 1. Concept of the Asian Highway Network……………………………… 1 2. Identifying the Network………………………………………………. 2 3. Current status of the Asian Highway………………………………….. 3 4. Formalization of the Asian Highway Network……………………….. 7 5. Promotion of the Asian Highway……………………………………... 9 6. A Vision of the Future………………………………………………… 10 II. ASIAN HIGHWAY ROUTES IN MEMBER COUNTRIES…... 16 1. Afghanistan……………………………………………………………. 16 2. Armenia……………………………………………………………….. 19 3. Azerbaijan……………………………………………………………... 21 4. Bangladesh……………………………………………………………. 23 5. Bhutan…………………………………………………………………. 27 6. Cambodia……………………………………………………………… 29 7. China…………………………………………………………………... 32 8. Democratic People’s Republic of Korea……………………………… 36 9. Georgia………………………………………………………………... 38 10. India…………………………………………………………………… 41 11. Indonesia………………………………………………………………. 45 12. Islamic Republic of Iran………………………………………………. 49 13 Japan…………………………………………………………………..
    [Show full text]
  • 9Th & 10Th Grade
    1/27/2019 SpeechWire Tournament Services Ridge Invitational Declamation (9th & 10th Grade) Elimination round results Final round All Judges Code Name Team LK1 WK1 AA1 All ranks Place recips pref. AH101 Niamh Campbell Phoenix Country Day School 1 1 6 14 6.67 1 LP103 Matthew Floyd Catholic Memorial 2 2 1 15 5.25 2 BD109 Ashin Varghese Randolph High School 3 3 2 16 5.42 3 AO121 Juliette Gringeri Summit High School 5 4 4 23 3.95 4 UT102 Farrah Culmer Democracy Prep Harlem Prep 7 6 3 24 4.48 5 AH108 Enzo Acharya Phoenix Country Day School 6 5 7 26 4.01 6 AG101 Brynn Nelson Fontbonne Hall Academy 4 7 5 26 3.84 7 Semifinal round All Judges Code Name Team AP2 BD1 All ranks Place recips pref. AH101 Niamh Campbell Phoenix Country Day School 1 1 6 4.50 1 BD109 Ashin Varghese Randolph High School 8 4.25 2 UT102 Farrah Culmer Democracy Prep Harlem Prep 8 3.83 3 AH108 Enzo Acharya Phoenix Country Day School 8 3.50 4 AG101 Brynn Nelson Fontbonne Hall Academy 10 3.25 5 AO121 Juliette Gringeri Summit High School 10 3.25 5 LP103 Matthew Floyd Catholic Memorial 2 2 10 3.25 5 AG102 Juliann Bianco Fontbonne Hall Academy 11 3.53 8 AL101 Adrian Tejada Democracy Prep Endurance High 11 3.00 9 AH112 Milan Sewell Phoenix Country Day School 12 2.58 10 BC115 Maria Chabanov Xaverian HS 13 2.08 11 AH109 Devan Amin Phoenix Country Day School 14 2.37 12 GG105 Uswad Qureshi Phillipsburg HS 14 2.33 13 AC107 Nina Li Strath Haven High School 3 4 14 1.92 14 BC116 Amy Gruber Xaverian HS 15 2.70 15 AH133 Ella Brenes Phoenix Country Day School 4 5 15 2.28 16 AM101 Jaina Jallow Livingston High School 5 3 15 1.87 17 AK108 Fatimata Ly Achievement First 17 2.60 18 CZ112 Rajit Sharma Union Catholic 17 2.03 19 Semifinal round All Judges Code Name Team AA5 RY3 All ranks Place recips pref.
    [Show full text]
  • The World's Colonisation and Trade Routes Formation As Imitated By
    The World's Colonisation and Trade Routes Formation as Imitated by Slime Mould Andrew Adamatzky University of the West of England, Bristol, United Kingdom This is unedited preprint with low-resolution photographs. Final and edited version of this paper is published in Int. J. Bifurcation Chaos, 22, 1230028 (2012) [26 pages] DOI: 10.1142/S0218127412300285 Abstract The plasmodium of Physarum polycephalum is renowned for spanning sources of nutrients with networks of protoplasmic tubes. The networks transport nutrients and metabolites across the plas- modium's body. To imitate a hypothetical colonisation of the world and formation of major trans- portation routes we cut continents from agar plates arranged in Petri dishes or on the surface of a three-dimensional globe, represent positions of selected metropolitan areas with oat flakes and inoculate the plasmodium in one of the metropolitan areas. The plasmodium propagates towards the sources of nutrients, spans them with its network of protoplasmic tubes and even crosses bare substrate between the continents. From the laboratory experiments we derive weighted Physarum graphs, analyse their structure, compare them with the basic proximity graphs and generalised graphs derived from the Silk Road and the Asia Highway networks. Keywords: biological transport networks, unconventional computing, slime mould 1 Introduction Nature-inspired computing paradigms and experimental laboratory prototypes are demonstrated reason- able success in approximation of shortest, and often collision-free, paths between two given points in an arXiv:1209.3958v1 [nlin.AO] 18 Sep 2012 Euclidean space or a graph. Examples include ant-based optimisation of communication networks [15], approximation of a shortest path in experimental reaction-diffusion chemical systems [1], gas-discharge analog systems [35], spatially extended crystallisation systems [5], fungi mycelia networks [22], and maze solving by Physarum polycephalum [29].
    [Show full text]