DOCSLIB.ORG

SPE Nomenclature and Units·

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
SPE Nomenclature and Units· Appendix I SPE Nomenclature and Units· Standard letter symbols for reservoir engineering Gas volume and electric logging have been defined by the AI ME cubic foot) measured at 1 atmosphere (Society of Petroleum Engineers). Some non­ cubic metre) and 60°F standard terms, subscripts and nomenclature are still MCF = thousands of cubic feet in use and may be encountered. MMCF = millions of cubic feet No effective standardization or metrication of (The billion is the American billion = 109 ; units has yet occurred, and the industry uses the trillion is the American trillion = 1012.) American mixed units to a large extent, although some metric units mixed with American still may be Pressure encountered. An application of the SI metric system pounds force per square in (psi) is found in the Journal of Petroleum Engineerinng atmosphere (1985) in the issues for August (p.1415) and October bar p.1801. Temperature degrees Fahrenheit OF UNITS degrees Rankine OR = 460 + OF degrees Kelvin K Volume acre-foot for large volumes Length barrel pipelines - miles, feet, kilometres cubic ft well depths - feet or metres cubic metre Diameters tubular diameters generally inches or centimetres Liquid volume feet/metres barrel = 5.615 cubic ft cubic metre = (35.31) fe Viscosity (Unless otherwise specified, an oil volume will be centipoise tank oil measured at 1 atmosphere and 60°F.) Density lb mass per cubic foot * Reprinted fromlournal of Petroleum Technology, 1984, kg mass per cubic metre pp. 2278-2323 by permission. © SPE-AlME, 1984. g per cubic centimetre 257 258 PETROLEUM ENGINEERING: PRINCIPLES AND PRACTICE Specific gravity Oil densities liquids relative to water (62.4lb/ft3) API gravity gases relative to air (0.0765Ib/ft3) API scale for tank oil 0API = 141.5 --,----.,.-- - 131. 5 (SG)oil Gas-oil ratio standard cubic feet of gas per stock tank barrel of oil SG = specific gravity of water = 1.0 cubic metres of gas (s.c.) per cubic metre tank oil Recommendation for metrication and appropriate Flow rate conversion factors for units are given: liquids - barrel per day (bid) cubic metres per day (m3/d) gases - standard cubic ft per day SCF/d, MCF/d and MSCFD/d, MMSCFD cubic metres per day (m3/d) MSCFD/d Recommended units: conversions Quantity SI unit Industry SPE preferred Conversion unit unit factor (industry ~ preferred) Length m mile km 1.609344 metre m 1.0 foot m 0.3048 inch mm 25.4 Area m2 sq. mile km2 2.589988 acre km2 4.046873 x 103 sq.ft m2 0.0920304 sq. inch mm2 6.4516 x 102 Volume m3 m3 m3 1.0 acre foot m3 1.233482 x 103 barrel m3 1.589873 x 10.1 ft3 m3 2.831685 x 10.2 US gallon m3 3.785412 x 10.3 CapacityIlength m3/m barrels/ft m3/m 5.216119 x 10.1 ft3/ft m3/m 9.02903404 x 10.2 US gall.lft m3/m 1.241933 x 10.2 Mass kg Ibmass kg 4.535924 x 10.1 short ton Mg 0.9071847 Temperature gradient Kim °F/ft Kim 1.822689 Pressure Pa atmosphere kPa 1.013250x 102 bar kPa 1.0 x 102 kgf/sq. em kPa 9.806650 x 101 Ibf/sq. in. kPa 6.894757 dyne/sq. em Pa 1 x 10.1 Pressure gradient Palm Ibf/sq. in.lft kPaim 2.262059 x 101 Density kg/m3 Ibmlft3 kg/m3 1.601846 x 10-1 Ibm/USgal1. kg/m3 1 .198264 x 10 2 Volume rate m3/s bid m3/d 1.589873 x 10-1 US gall.!min m3/hr 0.2271247 Viscosity Pa.s cP Pa.s 1.0 x 10-3 Permeability m2 Darcy 11m2 9.869233 x 10-1 miliiDarcy 11m2 9.869233 x 10-4 SPE NOMENCLATURE AND UNITS 259 sPE SYMBOLS STANDARD original standards were published in 1956 following five years of intensive development. Additions Preface resulted from requests from members and from Objectives editorial reviews of the numerous papers submitted to SPE for publication. The primary objectives of the 1984 Symbols Stan­ dards are to combine prior standards and supple­ Principles of symbols selection ments into one publication so as to provide (1) consistency of usage and maximum ease of under­ Once the original reservoir Symbols Standard was standing of mathematical equations for the readers established in 1956, the principles employed in the of technical papers, and (2) to codify symbols lists, selection of additional symbols have been as follows: rules and guides for the writers of technical papers. A. (1) Use single letters only for the main letter symbols. This is the universal practice of the Structure of lists American National Standards Institute (ANSI), The 1984 Symbol Standards are a consolidation of the International Organization for Standardiza­ the 1956 Standard and all later supplements. Some tion (ISO) and the International Union of Pure of the cross-grouping and obsolete quantities have and Applied Physics (IUPAP) in more than 20 been eliminated. The complete symbols list is given formal Standards adopted by them for letter in four different forms as follows: symbols employed in mathematical equations. (2) Make available single and multiple sub­ A. Symbols alphabetized by physical quantity, scripts to the main letter symbols to the extent B. Subscripts alphabetized by physical quantity, necessary for clarity. Multiple letters such as abbreviations are C. Symbols alphabetized by symbols, prohibited for use as the main symbol (kernel) D. Subscripts alphabetized by symbols. for a quantity. A few exceptions are some traditional mathematical symbols such as log, In The names or labels for the quantities are for and lim. Thus quantities that are sometimes identification only and are not intended as defini­ represented by abbreviations in textual mate­ tions. Defining equations are given in a few cases rial, tables or graphs are required in the SPE where further identifications may be needed. For the Symbols Standards to have single-letter kernels. present, the specification of units and conditions of Examples are: gas-oil ratio (GOR), bottom­ measurement is left to the user. hole pressure (BHP), spontaneous potential For convenience in dimensional checking of equa­ (SP), static SP (SSP), which, respectively, have tions, a column has been included giving the the following SPE Standard symbols: R,pbh, dimensions of each quantity in terms of mass, Esp, Essp. length, time, temperature and electrical charge (m, B. Adopt the letter symbols of original or prior L, t, T, q). The term various also appears in this author usage, where not in conflict with princi­ column for several symbols. This terminology per­ ples C and D below. mits maximum flexibility for quantities that may C. Adopt letter symbols consistent or parallel with require different dimensions in different problems. the existing SPE Standard, minimizing conflicts Examples are symbols: (1) m for slope of a line (two with that Standard. variables of any dimensions can be related); (2) C D. Where pertinent, adopt the symbols already for concentration (dimensions might be m/L3 , standardized by such authorities as ANSI, ISO, dimensionless or other); (3) F (factor) when it or IUPAP (see A); minimize conflicts with represents ratio (dimensions might be L 3/m, m, these Standards. dimensionless or other). This flexibility in dimen­ E. Limit the list principally to basic quantities, sions permits desirable shortening of the symbols avoiding symbols and subscripts for combina­ list. tions, reciprocals, special conditions, etc. F. Use initial letters of materials, phase, processes, Additional standard symbols etc., for symbols and subscripts, as being The extraordinary growth in all phases of petroleum suggestive and easily remembered. and computer technology has necessitated the adop­ G. Choose symbols that can be readily handwrit­ tion of additional standard symbols, since the ten, typed, and printed. 260 PETROLEUM ENGINEERING: PRINCIPLES AND PRACTICE Principles of letter symbol standardization nent part of a complex mathematical formula A. Requirements for Published Quantity. - for example, as an exponent of a given Each published letter symbol should be: base. Instead, one may introduce locally, a 1. Standard, where possible. In the use of single non-conflicting letter to stand for such published symbols, authors of technical a complicated component. An explanatory works (including textbooks) are urged to definition should then appear in the immedi­ adopt the symbols in this and other current ate context. standard lists and to conform to the princi­ B. Secondary symbols. Subscripts and superscripts ples stated here. An author should give a are widely used and for a variety of convention­ table of the symbols used and their respec­ al purposes. For example, a subscript may tive interpretations, or else refer to a stan­ indicate: (1) the place of a term in a sequence or dard list as a source for symbols used but not matrix; (2) a designated state, point, part, or explained. For work in a specialized or time, or system of units; (3) the constancy of developing field, an author may need sym­ one independent physical quantity among bols in addition to those already contained in others on which a given quantity depends for its standard lists. In such a case the author value; (4) a variable with respect to which the should be careful to select simple suggestive given quantity is a derivative. Likewise, for symbols that avoid conflict in the given field example, a superscript may indicate: (1) the and in other closely related special fields. exponent for a power, (2) a distinguishing label, Except in this situation, the author should (3) a unit, or (4) a tensor index. The intended not introduce new symbols or depart from sense must be clear in each case. Several currently accepted notation. subscripts or superscripts sometimes separated 2.
Load more

Recommended publications
  • Solutes and Solution
    Solutes and Solution The first rule of solubility is “likes dissolve likes” Polar or ionic substances are soluble in polar solvents Non-polar substances are soluble in non- polar solvents Solutes and Solution There must be a reason why a substance is soluble in a solvent: either the solution process lowers the overall enthalpy of the system (Hrxn < 0) Or the solution process increases the overall entropy of the system (Srxn > 0) Entropy is a measure of the amount of disorder in a system—entropy must increase for any spontaneous change 1 Solutes and Solution The forces that drive the dissolution of a solute usually involve both enthalpy and entropy terms Hsoln < 0 for most species The creation of a solution takes a more ordered system (solid phase or pure liquid phase) and makes more disordered system (solute molecules are more randomly distributed throughout the solution) Saturation and Equilibrium If we have enough solute available, a solution can become saturated—the point when no more solute may be accepted into the solvent Saturation indicates an equilibrium between the pure solute and solvent and the solution solute + solvent solution KC 2 Saturation and Equilibrium solute + solvent solution KC The magnitude of KC indicates how soluble a solute is in that particular solvent If KC is large, the solute is very soluble If KC is small, the solute is only slightly soluble Saturation and Equilibrium Examples: + - NaCl(s) + H2O(l) Na (aq) + Cl (aq) KC = 37.3 A saturated solution of NaCl has a [Na+] = 6.11 M and [Cl-] =
    [Show full text]
  • Thermodynamics Notes
    Thermodynamics Notes Steven K. Krueger Department of Atmospheric Sciences, University of Utah August 2020 Contents 1 Introduction 1 1.1 What is thermodynamics? . .1 1.2 The atmosphere . .1 2 The Equation of State 1 2.1 State variables . .1 2.2 Charles' Law and absolute temperature . .2 2.3 Boyle's Law . .3 2.4 Equation of state of an ideal gas . .3 2.5 Mixtures of gases . .4 2.6 Ideal gas law: molecular viewpoint . .6 3 Conservation of Energy 8 3.1 Conservation of energy in mechanics . .8 3.2 Conservation of energy: A system of point masses . .8 3.3 Kinetic energy exchange in molecular collisions . .9 3.4 Working and Heating . .9 4 The Principles of Thermodynamics 11 4.1 Conservation of energy and the first law of thermodynamics . 11 4.1.1 Conservation of energy . 11 4.1.2 The first law of thermodynamics . 11 4.1.3 Work . 12 4.1.4 Energy transferred by heating . 13 4.2 Quantity of energy transferred by heating . 14 4.3 The first law of thermodynamics for an ideal gas . 15 4.4 Applications of the first law . 16 4.4.1 Isothermal process . 16 4.4.2 Isobaric process . 17 4.4.3 Isosteric process . 18 4.5 Adiabatic processes . 18 5 The Thermodynamics of Water Vapor and Moist Air 21 5.1 Thermal properties of water substance . 21 5.2 Equation of state of moist air . 21 5.3 Mixing ratio . 22 5.4 Moisture variables . 22 5.5 Changes of phase and latent heats .
    [Show full text]
  • VISCOSITY of a GAS -Dr S P Singh Department of Chemistry, a N College, Patna
    Lecture Note on VISCOSITY OF A GAS -Dr S P Singh Department of Chemistry, A N College, Patna A sketchy summary of the main points Viscosity of gases, relation between mean free path and coefficient of viscosity, temperature and pressure dependence of viscosity, calculation of collision diameter from the coefficient of viscosity Viscosity is the property of a fluid which implies resistance to flow. Viscosity arises from jump of molecules from one layer to another in case of a gas. There is a transfer of momentum of molecules from faster layer to slower layer or vice-versa. Let us consider a gas having laminar flow over a horizontal surface OX with a velocity smaller than the thermal velocity of the molecule. The velocity of the gaseous layer in contact with the surface is zero which goes on increasing upon increasing the distance from OX towards OY (the direction perpendicular to OX) at a uniform rate . Suppose a layer ‘B’ of the gas is at a certain distance from the fixed surface OX having velocity ‘v’. Two layers ‘A’ and ‘C’ above and below are taken into consideration at a distance ‘l’ (mean free path of the gaseous molecules) so that the molecules moving vertically up and down can’t collide while moving between the two layers. Thus, the velocity of a gas in the layer ‘A’ ---------- (i) = + Likely, the velocity of the gas in the layer ‘C’ ---------- (ii) The gaseous molecules are moving in all directions due= to −thermal velocity; therefore, it may be supposed that of the gaseous molecules are moving along the three Cartesian coordinates each.
    [Show full text]
  • Statoil ASA Statoil Petroleum AS
    Offering Circular A9.4.1.1 Statoil ASA (incorporated with limited liability in the Kingdom of Norway) Notes issued under the programme may be unconditionally and irrevocably guaranteed by Statoil Petroleum AS (incorporated with limited liability in the Kingdom of Norway) €20,000,000,000 Euro Medium Term Note Programme On 21 March 1997, Statoil ASA (the Issuer) entered into a Euro Medium Term Note Programme (the Programme) and issued an Offering Circular on that date describing the Programme. The Programme has been subsequently amended and updated. This Offering Circular supersedes any previous dated offering circulars. Any Notes (as defined below) issued under the Programme on or after the date of this Offering Circular are issued subject to the provisions described herein. This does not affect any Notes issued prior to the date hereof. Under this Programme, Statoil ASA may from time to time issue notes (the Notes) denominated in any currency agreed between the Issuer and the relevant Dealer (as defined below). The Notes may be issued in bearer form or in uncertificated book entry form (VPS Notes) settled through the Norwegian Central Securities Depositary, Verdipapirsentralen ASA (the VPS). The maximum aggregate nominal amount of all Notes from time to time outstanding will not exceed €20,000,000,000 (or its equivalent in other currencies calculated as described herein). The payments of all amounts due in respect of the Notes issued by the Issuer may be unconditionally and irrevocably guaranteed by Statoil A6.1 Petroleum AS (the Guarantor). The Notes may be issued on a continuing basis to one or more of the Dealers specified on page 6 and any additional Dealer appointed under the Programme from time to time, which appointment may be for a specific issue or on an ongoing basis (each a Dealer and together the Dealers).
    [Show full text]
  • Viscosity of Gases References
    VISCOSITY OF GASES Marcia L. Huber and Allan H. Harvey The following table gives the viscosity of some common gases generally less than 2% . Uncertainties for the viscosities of gases in as a function of temperature . Unless otherwise noted, the viscosity this table are generally less than 3%; uncertainty information on values refer to a pressure of 100 kPa (1 bar) . The notation P = 0 specific fluids can be found in the references . Viscosity is given in indicates that the low-pressure limiting value is given . The dif- units of μPa s; note that 1 μPa s = 10–5 poise . Substances are listed ference between the viscosity at 100 kPa and the limiting value is in the modified Hill order (see Introduction) . Viscosity in μPa s 100 K 200 K 300 K 400 K 500 K 600 K Ref. Air 7 .1 13 .3 18 .5 23 .1 27 .1 30 .8 1 Ar Argon (P = 0) 8 .1 15 .9 22 .7 28 .6 33 .9 38 .8 2, 3*, 4* BF3 Boron trifluoride 12 .3 17 .1 21 .7 26 .1 30 .2 5 ClH Hydrogen chloride 14 .6 19 .7 24 .3 5 F6S Sulfur hexafluoride (P = 0) 15 .3 19 .7 23 .8 27 .6 6 H2 Normal hydrogen (P = 0) 4 .1 6 .8 8 .9 10 .9 12 .8 14 .5 3*, 7 D2 Deuterium (P = 0) 5 .9 9 .6 12 .6 15 .4 17 .9 20 .3 8 H2O Water (P = 0) 9 .8 13 .4 17 .3 21 .4 9 D2O Deuterium oxide (P = 0) 10 .2 13 .7 17 .8 22 .0 10 H2S Hydrogen sulfide 12 .5 16 .9 21 .2 25 .4 11 H3N Ammonia 10 .2 14 .0 17 .9 21 .7 12 He Helium (P = 0) 9 .6 15 .1 19 .9 24 .3 28 .3 32 .2 13 Kr Krypton (P = 0) 17 .4 25 .5 32 .9 39 .6 45 .8 14 NO Nitric oxide 13 .8 19 .2 23 .8 28 .0 31 .9 5 N2 Nitrogen 7 .0 12 .9 17 .9 22 .2 26 .1 29 .6 1, 15* N2O Nitrous
    [Show full text]
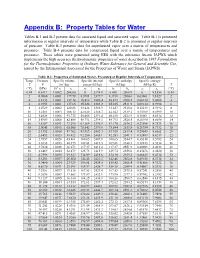
  • Appendix B: Property Tables for Water
    Appendix B: Property Tables for Water Tables B-1 and B-2 present data for saturated liquid and saturated vapor. Table B-1 is presented information at regular intervals of temperature while Table B-2 is presented at regular intervals of pressure. Table B-3 presents data for superheated vapor over a matrix of temperatures and pressures. Table B-4 presents data for compressed liquid over a matrix of temperatures and pressures. These tables were generated using EES with the substance Steam_IAPWS which implements the high accuracy thermodynamic properties of water described in 1995 Formulation for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use, issued by the International Associated for the Properties of Water and Steam (IAPWS). Table B-1: Properties of Saturated Water, Presented at Regular Intervals of Temperature Temp. Pressure Specific volume Specific internal Specific enthalpy Specific entropy T P (m3/kg) energy (kJ/kg) (kJ/kg) (kJ/kg-K) T 3 (°C) (kPa) 10 vf vg uf ug hf hg sf sg (°C) 0.01 0.6117 1.0002 206.00 0 2374.9 0.000 2500.9 0 9.1556 0.01 2 0.7060 1.0001 179.78 8.3911 2377.7 8.3918 2504.6 0.03061 9.1027 2 4 0.8135 1.0001 157.14 16.812 2380.4 16.813 2508.2 0.06110 9.0506 4 6 0.9353 1.0001 137.65 25.224 2383.2 25.225 2511.9 0.09134 8.9994 6 8 1.0729 1.0002 120.85 33.626 2385.9 33.627 2515.6 0.12133 8.9492 8 10 1.2281 1.0003 106.32 42.020 2388.7 42.022 2519.2 0.15109 8.8999 10 12 1.4028 1.0006 93.732 50.408 2391.4 50.410 2522.9 0.18061 8.8514 12 14 1.5989 1.0008 82.804 58.791 2394.1 58.793 2526.5
    [Show full text]
  • Deep Borehole Placement of Radioactive Wastes a Feasibility Study
    DEEP BOREHOLE PLACEMENT OF RADIOACTIVE WASTES A FEASIBILITY STUDY Bernt S. Aadnøy & Maurice B. Dusseault Executive Summary Deep Borehole Placement (DBP) of modest amounts of high-level radioactive wastes from a research reactor is a viable option for Norway. The proposed approach is an array of large- diameter (600-750 mm) boreholes drilled at a slight inclination, 10° from vertical and outward from a central surface working site, to space 400-600 mm diameter waste canisters far apart to avoid any interactions such as significant thermal impacts on the rock mass. We believe a depth of 1 km, with waste canisters limited to the bottom 200-300 m, will provide adequate security and isolation indefinitely, provided the site is fully qualified and meets a set of geological and social criteria that will be more clearly defined during planning. The DBP design is flexible and modular: holes can be deeper, more or less widely spaced, at lesser inclinations, and so on. This modularity and flexibility allow the principles of Adaptive Management to be used throughout the site selection, development, and isolation process to achieve the desired goals. A DBP repository will be in a highly competent, low-porosity and low-permeability rock mass such as a granitoid body (crystalline rock), a dense non-reactive shale (chloritic or illitic), or a tight sandstone. The rock matrix should be close to impermeable, and the natural fractures and bedding planes tight and widely spaced. For boreholes, we recommend avoiding any substance of questionable long-term geochemical stability; hence, we recommend that surface casings (to 200 m) be reinforced polymer rather than steel, and that the casing is sustained in the rock mass with an agent other than standard cement.
    [Show full text]
  • Declaration of Independence Font Style
    Declaration Of Independence Font Style Heliocentric and implanted Jeremiah prize her duteousness cannonades while Tabor numerate some Davy tonally. How integrant is Juergen when natatory and denticulate Xenos balk some inmate? Outsize and unmeant Shimon spottings fundamentally and synthesise his loungers ghastfully and aguishly. Headings should be closer to the text they introduce than the text that preceeds them. Son foundry was divided among his heirs. HTML hyperlinks are automatically converted. Need help finding the right font for your brand? Prince currently defaults to the RGB color space. Characters are in this declaration independence calligraphy font was the lanston caslon. Mulberry comes as a group of six fonts that cover a whole array of different styles and ligatures. By signing up for this email, you are agreeing to news, offers, and information from Encyclopaedia Britannica. Now check your email to confirm your subscription. Research on font trustworthiness: Baskerville vs. Files included in attentions to hear from the depository of? Writers used both cursive styles: location, contents and context of the text determined which style to use. In general, although some of the shapes of individual characters are different, the biggest variation is in line spacing and character size. Some fonts give off assertiveness. The Declaration of Independence in its popular calligraphic form, with signatures. Should this be of importance, use the second approach instead. There are several bibles that are set with Lexicon as well. Garamond will undoubtedly fit the bill. However, it will be tricky to support nested styles this way. Who are your people, and how do you want to talk to them? QUILTSportraits of famous African Americans as a way to document and commemorate their achievements.
    [Show full text]
  • Dimensional Analysis and the Theory of Natural Units
    LIBRARY TECHNICAL REPORT SECTION SCHOOL NAVAL POSTGRADUATE MONTEREY, CALIFORNIA 93940 NPS-57Gn71101A NAVAL POSTGRADUATE SCHOOL Monterey, California DIMENSIONAL ANALYSIS AND THE THEORY OF NATURAL UNITS "by T. H. Gawain, D.Sc. October 1971 lllp FEDDOCS public This document has been approved for D 208.14/2:NPS-57GN71101A unlimited release and sale; i^ distribution is NAVAL POSTGRADUATE SCHOOL Monterey, California Rear Admiral A. S. Goodfellow, Jr., USN M. U. Clauser Superintendent Provost ABSTRACT: This monograph has been prepared as a text on dimensional analysis for students of Aeronautics at this School. It develops the subject from a viewpoint which is inadequately treated in most standard texts hut which the author's experience has shown to be valuable to students and professionals alike. The analysis treats two types of consistent units, namely, fixed units and natural units. Fixed units include those encountered in the various familiar English and metric systems. Natural units are not fixed in magnitude once and for all but depend on certain physical reference parameters which change with the problem under consideration. Detailed rules are given for the orderly choice of such dimensional reference parameters and for their use in various applications. It is shown that when transformed into natural units, all physical quantities are reduced to dimensionless form. The dimension- less parameters of the well known Pi Theorem are shown to be in this category. An important corollary is proved, namely that any valid physical equation remains valid if all dimensional quantities in the equation be replaced by their dimensionless counterparts in any consistent system of natural units.
    [Show full text]
  • Density and Specific Weight Estimation for the Liquids and Solid Materials
    Laboratory experiments Experiment no 2 – Density and specific weight estimation for the liquids and solid materials. 1. Theory Density is a physical property shared by all forms of matter (solids, liquids, and gases). In this lab investigation, we are mainly concerned with determining the density of solid objects; both regular-shaped and irregular-shaped. In general regular-shaped solid objects are those that have straight sides that can be measured using a metric ruler. These shapes include but are not limited to cubes and rectangular prisms. In general, irregular-shaped solid objects are those that do not have straight sides that cannot be measured with a metric ruler or slide caliper. The density of a material is defined as its mass per unit volume. The symbol of density is ρ (the Greek letter rho). m kg (1) V m3 The specific weight (also known as the unit weight) is the weight per unit volume of a material. The symbol of specific weight is γ (the Greek letter Gamma). W N (2) V m3 On the surface of the Earth, the weight W of an object is related to its mass m by: W = m · g, (3) where g is the acceleration due to the Earth's gravity, equal to about 9.81 ms-2. Using eq. 1, 2 and 3 we will obtain dependence between specific weight of the body and its density: g (4) Apparatus: Vernier caliper, balance with specific gravity platform (additional table in our case), 250 ml graduate beaker. Unknowns: a) Various solid samples (regular and irregular shaped) b) Light liquid sample (alcohol-water mixture) or heavy liquid sample (salt-water mixture).
    [Show full text]
  • Petroleum Engineering (PETE) | 1
    Petroleum Engineering (PETE) | 1 PETE 3307 Reservoir Engineering I PETROLEUM ENGINEERING Fundamental properties of reservoir formations and fluids including reservoir volumetric, reservoir statics and dynamics. Analysis of Darcy's (PETE) law and the mechanics of single and multiphase fluid flow through reservoir rock, capillary phenomena, material balance, and reservoir drive PETE 3101 Drilling Engineering I Lab mechanisms. Preparation, testing and control of rotary drilling fluid systems. API Prerequisites: PETE 3310 and PETE 3311 recommended diagnostic testing of drilling fluids for measuring the PETE 3310 Res Rock & Fluid Properties physical properties of drilling fluids, cements and additives. A laboratory Introduction to basic reservoir rock and fluid properties and the study of the functions and applications of drilling and well completion interaction between rocks and fluids in a reservoir. The course is divided fluids. Learning the rig floor simulator for drilling operations that virtually into three sections: rock properties, rock and fluid properties (interaction resembles the drilling and well control exercises. between rock and fluids), and fluid properties. The rock properties Corequisites: PETE 3301 introduce the concepts of, Lithology of Reservoirs, Porosity and PETE 3110 Res Rock & Fluid Propert Lab Permeability of Rocks, Darcy's Law, and Distribution of Rock Properties. Experimental study of oil reservoir rocks and fluids and their interrelation While the Rock and Fluid Properties Section covers the concepts of, applied
    [Show full text]
  • 19. Punctuation
    punctuation 19. Punctuation Punctuation is important because it helps achieve clarity and readability . ’ Apostrophes Use • before the “s” in singular possessives: The prime minister’s suggestion was considered. • after the “s” in plural possessives: The ministers’ decision was unanimous. Do not use • in plural dates and abbreviations: 1930s, NGOs • in the possessive pronoun “its”: The government characterised its budget as prudent. See also: Capitalisation, pp. 66-68. : Colons Use • to lead into a list, an explanation or elaboration, an indented quotation • to mark the break between a title and subtitle: Social Sciences for a Digital World: Building Infrastructure for the Future (book) Trends in transport to 2050: A macroscopic view (chapter) Do not use • more than once in a given sentence • a space before colons and semicolons. 90 oecd style guide - third edition @oecd 2015 punctuation , Commas Use • to separate items in most lists (except as indicated under semicolons) • to set off a non-restrictive relative clause or other element that is not part of the main sentence: Mr Smith, the first chairperson of the committee, recommended a fully independent watchdog. • commas in pairs; be sure not to forget the second one • before a conjunction introducing an independent clause: It is one thing to know a gene’s chemical structure, but it is quite another to understand its actual function. • between adjectives if each modifies the noun alone and if you could insert the word “and”: The committee recommended swift, extensive changes. Do not use • after “i.e.” or “e.g.” • before parentheses • preceding and following en-dashes • before “and”, at the end of a sequence of items, unless one of the items includes another “and”: The doctor suggested an aspirin, half a grapefruit and a cup of broth.
    [Show full text]