DOCSLIB.ORG

U5 Determining Density

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
U5 Determining Density Presentation Name Course Name Unit # – Lesson #.# – Lesson Name Density • Density is a measure of the amount of matter per unit of volume Determining Density High Density Low Density – Objects more dense than water sink – Objects less dense than water float Matter: Mass vs. Weight Matter: Mass vs. Weight Mass and Weight are often confused • Mass is the amount of matter in an object or the • An example using SI units quantity of the inertia of the object – A man has a mass of 100 kg • Weight is the force of gravity on mass W = mg W = mg 2 W = (100 kg)(9.8 m/sec ) W = weight = 980 Newton m = mass g = acceleration of gravity – He weighs 980 N • Many materials are purchased by weight Project Lead The Way, Inc. Copyright 2010 1 Presentation Name Course Name Unit # – Lesson #.# – Lesson Name Matter: Mass vs. Weight Mass vs. Weight Mass and Weight are often confused • Pound-mass (lbm) is a unit of mass • US Customary units example . 1 lbm = 0.45359237 kg (by definition) – A woman weighs 100 pounds . 1 kg = 2.205 lbm (formula sheet) . 1 slug = 32.2 lbm (formula sheet) W = mg W Formula Sheet m = g 100 lb = = 3.1 slugs ft 32.2 s2 – Her mass is 3.1 slugs Mass vs. Weight Mass vs. Weight • Pound-force (lb) is a unit of force • How are pound-mass and pound-force . The gravitational force exerted on a mass of related? 2 one lbm on the surface of the Earth – On Earth (g = 32.174 ft/s ) . 1 lb = 4.44822162 N • 1 pound-mass object weighs1 pound-force . 1 N = 0.225 lb – In outer space (no gravity) • 1 pound-mass object has no weight Formula Sheet – On the moon (g = 5.32 ft/s2) • 1 pound-mass object weighs 0.166 pound-force Project Lead The Way, Inc. Copyright 2010 2 Presentation Name Course Name Unit # – Lesson #.# – Lesson Name Density Mass/Weight Density • Density can be indicated in multiple ways • Mass Density commonly used for SI units – Mass Density = mass per unit volume – g/cm3 or kg/m3 – Weight Density = weight per unit volume • Weight Density commonly used for US Formula Sheet Customary units – lb/in.3 or lb/ft3 m = VDm Material Mass Density Weight Density m 3 3 Dm = (g/cm ) (lb/in. ) V Apples 0.64 0.023 Water (Pure) 1.00 0.036 Water (Sea) 1.03 0.037 Ice 0.92 0.034 W = VDw Concrete 2.40 0.087 W Aluminum 2.71 0.098 D = w V Steel (1018) 7.8 0.282 Gold 19.32 0.698 Mass and Weight: Measurement Volume: Measurement • Balance – measures mass • Volume is the amount of three – Uses objects of known mass to find the dimensional space enclosed by unknown mass of an object an object – Measurement is unaffected by difference in gravity – Two methods to determine volume • Calculate using geometry of object • Scale – measures weight – Measures force caused by gravity – Measurement is affected by difference in the • Measure indirectly using water acceleration of gravity displacement (or 3D scanner) – May display a “mass” measurement reading by using an assumed acceleration of gravity to convert from weight to mass Project Lead The Way, Inc. Copyright 2010 3 Presentation Name Course Name Unit # – Lesson #.# – Lesson Name Volume: Calculation Volume: Indirect Measure • Some object volumes can be calculated • Volume of an irregular object can be • What is the volume formula for each object? determined indirectly with fluid displacement Level Elevates Volume: Indirect Measure Example • What is the density of a 1.12 in. diameter • Record water level with only water sphere of titanium that weighs 0.82 lb? • Add samples 4 V = π r3 • Record new level 3 W = VDw 4 • Difference is sample volume V = π 1.12 in. 3 W 0.82 lb 3 Dw = = V 5.88 in.3 V = 5.88 in3 Dw = 0.14 lb/in.3 Volume Read Change level • What volume of water (mL) would it displace? here 3 1 ft 1L 5.88 in.3 = 0.096 L or 96 mL 3 3 Meniscus shape is 1728 in. 0.0353 ft exaggerated for clarity Project Lead The Way, Inc. Copyright 2010 4 .
Load more

Recommended publications
  • 5 Military Rucking Rules Every Backpacker Should Know 1. One
    5 Military Rucking Rules Every Backpacker Should Know The military has spent years studying the best way to move under a load (aka “rucking”). Here are 5 military rucking rules that translate well to hikers. “Rucking” is the military term for hiking under load. As you can imagine, this is a huge issue for the military, as soldiers must wear body armor and carry weapons, ammo, water, communications equipment, and other gear as they conduct patrols and missions. Rucking performance and injury prevention are hugely important for military operations and personnel. Movement over ground under load is also a key for hiking and backpacking. In reviewing the research the military has already done on this subject, we discovered five rules. Read on to make sure you’re following these military rucking rules on your next backcountry adventure. 1. One pound on your feet equals five pounds on your back. This old backpacking thumb rule holds true, according to a 1984 study from the U.S. Army Research Institute. They tested how much more energy was expended with different footwear (boots and shoes) and concluded that it take 4.7 to 6.4 times as much energy to move at a given pace when weight is carried on the shoe versus on the torso. In practical terms, this means you could carry half a gallon more of water (a little over 4 pounds) if you buy boots that are a pound lighter, which isn’t hard to do; and that’s a lot of water. Now imagine the energy savings of backpacking in light trail running shoes rather than heavy, leather backpacking boots over the course of 7- day backpacking trip.
    [Show full text]
  • Weights and Measures Standards of the United States: a Brief History
    1 .0 11 8 1.25 1.4 I 6_ DOCUMENT RESUME ED 142 418 SE 022 719 AUTHOE Judson, Lewis V. TITLE Weights and Measures Standards of the United States: A Brief History. Updated Edition. INSTITUTION National Bureau of Standards (DOC) ,Washington, D.C. REPORT NO NBS-SP-447 PUB DATE Mar 76 NOTE 42p.; Contains occasional small print; Photographs may not reproduce well AVAILABLE FROM Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402 (Stock Number 003-0O3-01654-3, $1.00) EDRS PRICE MF-$0.83 HC-$2.06 Plus Postage. DESCRIPTORS Government Publications; History; *Mathematics Education; *Measurement; *Metric System; *Science History; *Standards ABSTRACT This document was published by the National Bureau of Standards to meet the current demand for information on the history of weights and measures in the United States. It includes an illustrated discussion of this history through 1962 followed by an addendum covering the period 1963-1975. Appendices provide a bibliography and photographic copies of eight documents important to the development of official standards of measurement. (SD) *********************************************************************** Documents acquired by ERIC include many informal unpublished * materials not available from other sources. ERIC makes every effort * * -to obtain the best copy available. Nevertheless, items of marginal * * reproducibility are often encountered and this affects the quality * * of the microfiche and hardcopy reproductions ERIC makes available * via the ERIC Document Reproduction Service (EDRS). EDRS is not * responsible for the quality of the original document. Reproductions * * supplied by EDRS are the best that can be made from the original. *********************************************************************** U.S. DEPARTMENT OF HEALTH.
    [Show full text]
  • Fundamentals of Math CHAPTER 1
    © Jones and Bartlett Publishers, LLC. NOT FOR SALE OR DISTRIBUTION Fundamentals of Math CHAPTER 1 OBJECTIVES ■ Understand the difference between the Arabic and Roman numeral systems ■ Translate Arabic numerals to Roman numerals ■ Translate Roman numerals to Arabic numerals ■ Understand the metric system ■ Understand the apothecary system ■ Be able to convert metric to apothecary ■ Be able to convert apothecary to metric ARABIC NUMERALS The Arabic number system uses the numerals 1, 2, 3, 4, 5, 6, 7, 8, 9, and zero (0). It is also known as the decimal system. Depending on how these numbers are arranged determines the value of the number. For example, digits 4, 7, and 2 placed together (472) represent the number four hundred seventy-two. A decimal point (.) separates whole numbers, or units, from fractional num- bers, or fractional units. All numbers on the left side of the decimal point are considered whole numbers. All numbers placed on the right of the decimal point are considered fractional units, or less than one whole unit. The following num- ber line shows the relationship of Arabic numerals based on their position in a number. Ten-thousands hundreds ones tenths thousandths hundred-thousandths -----5------8------2-----4-----3---- . ----6------7------9------3------2-------------- thousands tens hundredths ten-thousandths The number 43.6 contains the numerals 4, 3, and 6. This represents forty-three units of one and six-tenths of one unit. Decimals will be covered in more detail in Chapter 2. 1 59612_CH01_FINAL.indd 1 8/20/09 7:38:45 PM © Jones and Bartlett Publishers, LLC. NOT FOR SALE OR DISTRIBUTION 2 Chapter 1 ■ Fundamentals of Math ROMAN NUMERALS The Roman numeral system does not utilize numerals.
    [Show full text]
  • Student Academic Learning Services Pounds Mass and Pounds Force
    Student Academic Learning Services Page 1 of 3 Pounds Mass and Pounds Force One of the greatest sources of confusion in the Imperial (or U.S. Customary) system of measurement is that both mass and force are measured using the same unit, the pound. The differentiate between the two, we call one type of pound the pound-mass (lbm) and the other the pound-force (lbf). Distinguishing between the two, and knowing how to use them in calculations is very important in using and understanding the Imperial system. Definition of Mass The concept of mass is a little difficult to pin down, but basically you can think of the mass of an object as the amount of matter contain within it. In the S.I., mass is measured in kilograms. The kilogram is a fundamental unit of measure that does not come from any other unit of measure.1 Definition of the Pound-mass The pound mass (abbreviated as lbm or just lb) is also a fundamental unit within the Imperial system. It is equal to exactly 0.45359237 kilograms by definition. 1 lbm 0.45359237 kg Definition of Force≡ Force is an action exerted upon an object that causes it to accelerate. In the S.I., force is measured using Newtons. A Newton is defined as the force required to accelerate a 1 kg object at a rate of 1 m/s2. 1 N 1 kg m/s2 Definition of ≡the Pound∙ -force The pound-force (lbf) is defined a bit differently than the Newton. One pound-force is defined as the force required to accelerate an object with a mass of 1 pound-mass at a rate of 32.174 ft/s2.
    [Show full text]
  • Weights and Measures Standards of the United States—A Brief History (1963), by Lewis V
    WEIGHTS and MEASURES STANDARDS OF THE UMIT a brief history U.S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS NBS Special Publication 447 WEIGHTS and MEASURES STANDARDS OF THE TP ii 2ri\ ii iEa <2 ^r/V C II llinCAM NBS Special Publication 447 Originally Issued October 1963 Updated March 1976 For sale by the Superintendent of Documents, U.S. Government Printing Office Wash., D.C. 20402. Price $1; (Add 25 percent additional for other than U.S. mailing). Stock No. 003-003-01654-3 Library of Congress Catalog Card Number: 76-600055 Foreword "Weights and Measures," said John Quincy Adams in 1821, "may be ranked among the necessaries of life to every individual of human society." That sentiment, so appropriate to the agrarian past, is even more appropriate to the technology and commerce of today. The order that we enjoy, the confidence we place in weighing and measuring, is in large part due to the measure- ment standards that have been established. This publication, a reprinting and updating of an earlier publication, provides detailed information on the origin of our standards for mass and length. Ernest Ambler Acting Director iii Preface to 1976 Edition Two publications of the National Bureau of Standards, now out of print, that deal with weights and measures have had widespread use and are still in demand. The publications are NBS Circular 593, The Federal Basis for Weights and Measures (1958), by Ralph W. Smith, and NBS Miscellaneous Publication 247, Weights and Measures Standards of the United States—a Brief History (1963), by Lewis V.
    [Show full text]
  • Imperial Units
    Imperial units From Wikipedia, the free encyclopedia Jump to: navigation, search This article is about the post-1824 measures used in the British Empire and countries in the British sphere of influence. For the units used in England before 1824, see English units. For the system of weight, see Avoirdupois. For United States customary units, see Customary units . Imperial units or the imperial system is a system of units, first defined in the British Weights and Measures Act of 1824, later refined (until 1959) and reduced. The system came into official use across the British Empire. By the late 20th century most nations of the former empire had officially adopted the metric system as their main system of measurement. The former Weights and Measures office in Seven Sisters, London. Contents [hide] • 1 Relation to other systems • 2 Units ○ 2.1 Length ○ 2.2 Area ○ 2.3 Volume 2.3.1 British apothecaries ' volume measures ○ 2.4 Mass • 3 Current use of imperial units ○ 3.1 United Kingdom ○ 3.2 Canada ○ 3.3 Australia ○ 3.4 Republic of Ireland ○ 3.5 Other countries • 4 See also • 5 References • 6 External links [edit] Relation to other systems The imperial system is one of many systems of English or foot-pound-second units, so named because of the base units of length, mass and time. Although most of the units are defined in more than one system, some subsidiary units were used to a much greater extent, or for different purposes, in one area rather than the other. The distinctions between these systems are often not drawn precisely.
    [Show full text]
  • English Customary Weights and Measures
    English Customary Weights and Measures Distance In all traditional measuring systems, short distance units are based on the dimensions of the human body. The inch represents the width of a thumb; in fact, in many languages, the word for "inch" is also the word for "thumb." The foot (12 inches) was originally the length of a human foot, although it has evolved to be longer than most people's feet. The yard (3 feet) seems to have gotten its start in England as the name of a 3-foot measuring stick, but it is also understood to be the distance from the tip of the nose to the end of the middle finger of the outstretched hand. Finally, if you stretch your arms out to the sides as far as possible, your total "arm span," from one fingertip to the other, is a fathom (6 feet). Historically, there are many other "natural units" of the same kind, including the digit (the width of a finger, 0.75 inch), the nail (length of the last two joints of the middle finger, 3 digits or 2.25 inches), the palm (width of the palm, 3 inches), the hand (4 inches), the shaftment (width of the hand and outstretched thumb, 2 palms or 6 inches), the span (width of the outstretched hand, from the tip of the thumb to the tip of the little finger, 3 palms or 9 inches), and the cubit (length of the forearm, 18 inches). In Anglo-Saxon England (before the Norman conquest of 1066), short distances seem to have been measured in several ways.
    [Show full text]
  • Dimensions and Units English Units of Measurement Units of Weight
    English units of measurement Today: A system of weights and measures used in a few nations, the only major industrial one Chapter 6 continued: being the United States. It actually consists of Dimensions and Units two related systems—the U.S. Customary System of units, used in the United States and dependencies, and the British Imperial System. Units of Weight The pound (lb) is the basic unit of weight (which is proportional to mass) (how?). Within the English units of measurement there are three different systems of weights. In the avoirdupois system, the most widely used of Question: the three, the pound is divided into 16 ounces (oz) and the ounce into 16 drams. The ton, used Is there a problem? to measure large masses, is equal to 2,000 lb (short ton) or 2,240 lb (long ton). In Great Britain the stone, equal to 14 lb, is also used. “weight is proportional to mass.” Answer: You need to be aware of Force = Mass* Acceleration the law governing that proportionality: Newton’s Law Acceleration is NOT a constant, mass is. Force = Mass* Acceleration Even on earth, g = 9.81 m/s2 is NOT constant, but varies with latitude and Question: elevation. Is there a problem? “weight is proportional to mass.” “weight is proportional to mass.” 1 Another problem arises from the A mass is NEVER a “weight”. common intermingling of the terms “mass” and “weight”, as in: Force = Mass* Acceleration “How much does a pound of mass weigh?” Or: “If you don’t know whether it’s pound- “Weight” = Force mass or pound-weight, simply say pounds.” “Weight” = Force Forces in SI Units …because on earth all masses are 2 exposed to gravity.
    [Show full text]
  • Measurement Units • a Pound Mass of Steam Releases Approximately 1000 Btu When Condensed
    Measurement Units • A pound mass of steam releases approximately 1000 Btu when condensed. • Condensate at about 200F contains an additional 170 Btu – about 100 Btu is usable • Saturated steam is typically measured in units of mass. 1 Mlb = 1000 lb of steam = about 1 MmBtu • Superheated steam may be measured in units of heat – MmBtu. Metering Options • Volumetric steam flow at a fixed or assumed density • Steam mass flow based on volumetric flow and active density compensation (temperature and/or pressure compensated) • Volumetric condensate flow with fixed or active density compensation Steam • Differential pressure – orifice plate, venturi, nozzle, averaging pitot tube, variable aperture • Oscillatory – Vortex shedder bar, Multi- variable vortex • Positive Displacement – insertion type turbine wheel • Others - Ultrasonic, coriolis, target Condensate • Positive displacement – turbine, nutating disc water meter • Magnetic • Ultrasonic • Bucket Type – Cadillac, Lincoln • Oscillatory – Vortex shedder bar • Relatively low cost and good accuracy • Easy to properly size – just change the orifice • Well established physics and math • Very wide range of suppliers • Limited turndown due to square law – 10:1 flow range = 100:1 DP range • Anything less than perfect impulse line construction can lead to large errors • Calibration and PM is more difficult and can add to ownership cost • Typically used on > 8 inch line sizes and in applications with relatively constant flow • High and low flow (winter/summer) flow stations often required in building applications. • Moderate cost and very good accuracy • Better turndown than DP – 20:1, but output drops to zero at low velocities • Well established physics and math • Very wide range of suppliers • Calibration is very simple and virtually no PM required.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
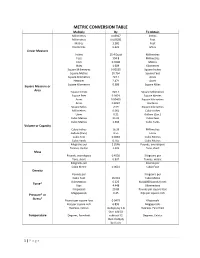
  • Metric Conversion Table
    METRIC CONVERSION TABLE Multiply By To Obtain Millimetres 0.03937 Inches Millimetres 0.003281 Feet Metres 3.281 Feet Kilometres 0.621 Miles Linear Measure Inches 25.4 Exact Millimetres Feet 304.8 Millimetres Feet 0.3048 Metres Miles 1.609 Kilometres Square Millimetres 0.00155 Square Inches Square Metres 10.764 Square Feet Square Kilometres 247.1 Acres Hectares 2.471 Acres Square Kilometres 0.386 Square Miles Square Measure or Area Square Inches 645.2 Square Millimetres Square Feet 0.0929 Square Metres Acres 0.00405 Square Kilometres Acres 0.4047 Hectares Square Miles 2.59 Square Kilometres Millimetres 0.061 Cubic Inches Litres 0.22 Gallons (Can.) Cubic Metres 35.31 Cubic Feet Cubic Metres 1.308 Cubic Yards Volume or Capacity Cubic Inches 16.39 Millimetres Gallons (Can.) 4.55 Litres Cubic Feet 0.0283 Cubic Metres Cubic Yards 0.765 Cubic Metres Kilograms per 2.2046 Pounds, avoirdupois Tonnes, metric 1.102 Tons, short Mass Pounds, avoirdupois 0.4536 Kilograms per Tons, short 0.907 Tonnes, metric Kilograms per Pounds per Cubic Metre 0.0624 Cubic Foot Density Pounds per Kilograms per Cubic Foot 16.019 Cubic Metre Kilonewtons 0.225 Kips(1000 ponds force) Force* Kips 4.448 Kilonewtons Kilopascals 20.89 Pounds per square foot Megapascals 0.45 Kips per square inch Pressure* or Stress* Pounds per square foot 0.0479 Kilopascals Kips per square inch 6.895 Megapascals Degrees, Celsius multiply by 1.8 Degrees, Farenheit then add 32 Temperature Degrees, Farenheit subtract 32 Degrees, Celsius then multiply by 0.555 1 | P a g e METRIC CONVERSION GUIDE Linear Measurement One millimetre (1 mm) is equal to a thousandth part of a metre (0.001 m) and is a little greater than 1/32”.
    [Show full text]
  • Introduction to Mechanical Engineering Measurements Author: John M
    Introduction, Page 1 Introduction to Mechanical Engineering Measurements Author: John M. Cimbala, Penn State University Latest revision, 19 August 2011 Two Main Purposes of Measurements Engineering experimentation - This is where we seek new information, and is generally done when developing a new product. Some example questions which may be asked by the engineer are: How hot does it get? How fast does it go? Operational systems - This is where we monitor and control processes, generally on existing equipment rather than in the design of new products. For example, consider the heating and/or air conditioning control system in a room. The system measures the temperature, and then controls the heating or cooling equipment. Dimensions and Units Primary (or Basic) Dimensions There are seven primary dimensions (also called basic dimensions). All other dimensions can be formed by combinations of these. The primary dimensions are: mass, length, time, temperature, current, amount of light, and amount of matter. Unit Systems Unit systems were invented so that numbers could be assigned to the dimensions. o There are three primary unit systems in use today: . the International System of Units (SI units, from Le Systeme International d’Unites, more commonly simply called the metric system of units) . the English Engineering System of Units (commonly called English system of units) . the British Gravitational System of Units (BG) o The latter two are similar, except for the choice of primary mass unit and use of the degree symbol. The two dominant unit systems in use in the world today are the metric system (SI) and the English system.
    [Show full text]