DOCSLIB.ORG

Greek ‘Cultural Translation’ of Chaldean Learning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Greek ‘Cultural Translation’ of Chaldean Learning GREEK ‘CULTURAL TRANSLATION’ OF CHALDEAN LEARNING by MOONIKA OLL A Thesis Submitted to The University of Birmingham For the Degree of DOCTOR OF PHILOSOPHY Department of Classics, Ancient History and Archaeology School of History and Cultures College of Arts and Law The University of Birmingham May 2014 University of Birmingham Research Archive e-theses repository This unpublished thesis/dissertation is copyright of the author and/or third parties. The intellectual property rights of the author or third parties in respect of this work are as defined by The Copyright Designs and Patents Act 1988 or as modified by any successor legislation. Any use made of information contained in this thesis/dissertation must be in accordance with that legislation and must be properly acknowledged. Further distribution or reproduction in any format is prohibited without the permission of the copyright holder. Abstract The investigation into the relationship between Greek and Babylonian systems of learning has overwhelmingly focused on determining the elements that the former borrowed from the latter, while the fundamental questions relating to the process of transmission of these elements are still largely ignored. This thesis, therefore, offers a preliminary theoretical framework within which the movement of ideas should be analysed. The framework is based on the understanding that all ideas from one culture, when they are to enter another thought and belief system, must be ’translated’ into the concepts and terminology prevalent in their new context. An approach is developed which exploits the concept of ’cultural translation’ as put forward within various modern disciplines. The thesis examines how the ’translatability’ of the material from the perspective of the receiving culture influences its inclusion into the new ’home repertoire’ and determines the changes it undergoes as part of this process. A number of case studies in astronomy, astrology and mathematics are presented to help explain what parts of ’Chaldean knowledge’ were utilised by Greek and Hellenistic scholars, how these were interpreted according to the existing Greek intellectual network into which the new material was inserted and how it was influenced by the ’cultural grid’, a construct reflecting patterns of expectation about a foreign culture. Acknowledgements I would like to thank the Arts and Humanities Research Council without whose generous financial support this study would have never seen the light of day. No smaller amount of gratitude goes to my supervisor Prof. Ken Dowden, not just for his invaluable help, guidance and endless enthusiasm, but most of all for believing in my academic ability long before I learned to believe in it myself. His trust and patience over the last months, and his willingness to then correct the final draft in such a short period of time, have been humbling, his insights into the ancient world and especially the way we study it today have inspired me since he first agreed to supervise my undergraduate dissertation. And for this I am indebted to Dr. Martin Bommas and Dr. Gideon Nisbet, who, I suspect, gave me the necessary recommendation. Thanks are also due to all other members of staff who have helped and inspired me over the years, and scholars from other institutions who have kindly shared with me their unpublished work or articles I would not have had access to otherwise. As so often happens in academic life, people have come into my life very suddenly and drifted out of it as fast. I wish I could thank everyone who has helped and entertained me during my time here in Birmingham: my colleagues, my housemates and all friends I have made over the years, but they are too numerous to name individually. Yet, a few have created such vivid memories and made me not just a better scholar, but a better and braver person, that they deserve special mention. First of all, Carlo and Matt, who never failed to make me laugh and, although it is hard for me to admit, provided me with a social life. Alaa, whose very brave life-choices have taught me to just get on with it. And Magda, who succumbed to my blackmail and bribery and helped me with those tedious final checks and who has kept me sane and grounded in the real world. I also wish to thank my family, even if they still have little to no idea about what I have been doing for the past four years. They have always respected and supported my (somewhat unreasonable) choices and I have aspired to make them proud. They have always believed in me and been there for me, although I have been so far from them for so long. I also take full responsibility for the fact that none of my three very talented younger brothers will ever follow my footsteps into academia. And finally, I want to thank my friends at home for not having given up on me as a person. Contents Abbreviations ............................................................................................................................................ i Introduction ............................................................................................................................................ 1 Chapter 1: The Theory of Cultural Translation ........................................................................................ 9 1.1 Introduction................................................................................................................................... 9 1.2 The Concept of Cultural Translation and Historical Studies ........................................................ 11 1.3 Research Framework of Cultural Translation .............................................................................. 14 1.3.1 Dynamics of Knowledge Acquisition and Diffusion .............................................................. 14 1.3.2 Creation of Meaning............................................................................................................. 16 1.3.3 Primary Cultural Translation Against an Existing Scientific Grid .......................................... 17 1.3.4 Onward Development Conditioned by the Cultural and Intellectual Koinē ........................ 20 1.4 Conclusion ................................................................................................................................... 23 Chapter 2: Chaldea and the Near East as Greek Cultural Concepts ...................................................... 25 2.1 Introduction................................................................................................................................. 25 2.2 Intellectual Context and Extra-Textual Constraints .................................................................... 26 2.2.1 Sources of Oral Traditions during the Archaic Period .......................................................... 26 2.2.2 From Oral to Literary History ............................................................................................... 34 2.2.3 The Barbarian Stereotype and Literary Topoi ...................................................................... 39 2.3 Individual Erzählmotive of the Babylonian Logoi ........................................................................ 46 2.3.1 Babylonian Bride-Market and Temple Prostitution ............................................................. 46 2.3.2 Legendary Rulers from Ninus to Sardanapallos ................................................................... 53 2.3.3 The Hanging Gardens ........................................................................................................... 71 2.3.4 Antiquity of Knowledge and the Emergence of Science ...................................................... 77 2.4 Conclusion ................................................................................................................................... 93 Chapter 3: Astronomy ........................................................................................................................... 96 3.1 Introduction................................................................................................................................. 96 3.2 ‘The Source Text’ – Mesopotamian Astronomical Tradition....................................................... 97 3.2.1 Early Mesopotamian Astronomy – Ideas and Ideals ............................................................ 97 3.2.2 Towards More Accurate Functions .................................................................................... 105 3.2.3 Mesopotamian Mathematical Astronomy ......................................................................... 108 3.3 Greek Reckoning of Time: Parapēgmata and the Intercalation Cycles ..................................... 116 3.4 ‘Home Repertoire’ – from Cosmological Speculation to Mathematical Astronomy ................ 125 3.4.1 Hipparchus (c.190-120 BC) ................................................................................................. 138 3.4.2 Linear Methods of Practical Astronomy ............................................................................. 149 3.5 Conclusions................................................................................................................................ 157 Chapter 4: Astrology ........................................................................................................................... 162 4.1 Introduction............................................................................................................................... 162 4.2
Load more

Recommended publications
  • The Satrap of Western Anatolia and the Greeks
    University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations 2017 The aS trap Of Western Anatolia And The Greeks Eyal Meyer University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Ancient History, Greek and Roman through Late Antiquity Commons Recommended Citation Meyer, Eyal, "The aS trap Of Western Anatolia And The Greeks" (2017). Publicly Accessible Penn Dissertations. 2473. https://repository.upenn.edu/edissertations/2473 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/2473 For more information, please contact [email protected]. The aS trap Of Western Anatolia And The Greeks Abstract This dissertation explores the extent to which Persian policies in the western satrapies originated from the provincial capitals in the Anatolian periphery rather than from the royal centers in the Persian heartland in the fifth ec ntury BC. I begin by establishing that the Persian administrative apparatus was a product of a grand reform initiated by Darius I, which was aimed at producing a more uniform and centralized administrative infrastructure. In the following chapter I show that the provincial administration was embedded with chancellors, scribes, secretaries and military personnel of royal status and that the satrapies were periodically inspected by the Persian King or his loyal agents, which allowed to central authorities to monitory the provinces. In chapter three I delineate the extent of satrapal authority, responsibility and resources, and conclude that the satraps were supplied with considerable resources which enabled to fulfill the duties of their office. After the power dynamic between the Great Persian King and his provincial governors and the nature of the office of satrap has been analyzed, I begin a diachronic scrutiny of Greco-Persian interactions in the fifth century BC.
    [Show full text]
  • Sample Pages
    SECTION ONE: ENTRIES Invasions and Conquests_P1-001-158.indd 1 10/28/16 5:43 PM Invasions and Conquests_P1-001-158.indd 2 10/28/16 5:43 PM THE ANCIENT WORLD Assyrian Empire Canaan, Israelite Invasion of Chaldean (Neo-Babylonian) Empire, Expansion of Cyrus The Great Egypt, Hyksos Invasion of Hittites, Expansion of India, Aryan Invasion of Kush, Expansion of Palestine, Egyptian Invasions of Persian Empire, Expansion of Sargon The Great (Z) Chou Dynasty, Expansion of Invasions and Conquests_P1-001-158.indd 3 10/28/16 5:43 PM WARFARE IN THE ANCIENT WORLD As soon as man learned to use rocks and sharp sticks to hunt for meat he probably realized that such weapons could be used to impose his will on other people. The earliest for of warfare was brute muscle power with those throwing the most accurate stone or swinging the heaviest club enjoying the advan- tage. Over time, people realized that a sharp rock or stick was more effective than a dull one, so how to create and maintain that sharp edge came to be a major goal in weapon development. Using rocks as a projectile became more effective when someone realized that they could go further and faster when thrown by a long piece of leather. The development of the sling created the ability to harass and harm one’s enemy at great range, hurting him while keeping oneself safe. Slingers became important units in ancient armies and men talented in its use were in demand as mercenaries. In order to maintain a steady supply of projectiles of proper size and weight, rocks were supplanted by pellets made of baked clay and later of lead.
    [Show full text]
  • Public Finance and Democratic Ideology in Fourth-Century BC Athens by Christopher Scott Welser BA, Sw
    Dēmos and Dioikēsis: Public Finance and Democratic Ideology in Fourth-Century B.C. Athens By Christopher Scott Welser B.A., Swarthmore College, 1994 M.A., University of Maryland, 1999 Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of Classics at Brown University, Providence, Rhode Island. May, 2011 © Copyright 2011 by Christopher Scott Welser This dissertation by Christopher Scott Welser is accepted in its present form by the Department of Classics as satisfying the dissertation requirement for the degree of Doctor of Philosophy. Date________________ _______________________________________ Adele C. Scafuro, Advisor Recommended to the Graduate Council Date________________ _______________________________________ Alan L. Boegehold, Reader Date________________ _______________________________________ David Konstan, Reader Approved by the Graduate Council Date________________ _______________________________________ Peter M. Weber, Dean of the Graduate School iii CURRICULUM VITAE Christopher Scott Welser was born in Romeo, Michigan in 1971. He attended Roeper City and Country School in Bloomfield Hills, Michigan, and in 1994 he graduated from Swarthmore College, earning an Honors B.A. in Economics (his major) and Biology (his minor). After working for several years at public policy research firms in Pennsylvania and New Jersey, he decided to pursue the study of Classics, an interest of his since childhood. Upon earning an M.A. with Distinction in Latin and Greek from the University of Maryland at College Park in 1999, he enrolled in the Ph.D. program in Classics at Brown University. While working on his Ph.D., he spent two years as Seymour Fellow (2002-2003) and Capps Fellow (2004-2005) at the American School of Classical Studies at Athens and participated in the summer program of the American Academy in Rome (2000).
    [Show full text]
  • Meet the Philosophers of Ancient Greece
    Meet the Philosophers of Ancient Greece Everything You Always Wanted to Know About Ancient Greek Philosophy but didn’t Know Who to Ask Edited by Patricia F. O’Grady MEET THE PHILOSOPHERS OF ANCIENT GREECE Dedicated to the memory of Panagiotis, a humble man, who found pleasure when reading about the philosophers of Ancient Greece Meet the Philosophers of Ancient Greece Everything you always wanted to know about Ancient Greek philosophy but didn’t know who to ask Edited by PATRICIA F. O’GRADY Flinders University of South Australia © Patricia F. O’Grady 2005 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise without the prior permission of the publisher. Patricia F. O’Grady has asserted her right under the Copyright, Designs and Patents Act, 1988, to be identi.ed as the editor of this work. Published by Ashgate Publishing Limited Ashgate Publishing Company Wey Court East Suite 420 Union Road 101 Cherry Street Farnham Burlington Surrey, GU9 7PT VT 05401-4405 England USA Ashgate website: http://www.ashgate.com British Library Cataloguing in Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask 1. Philosophy, Ancient 2. Philosophers – Greece 3. Greece – Intellectual life – To 146 B.C. I. O’Grady, Patricia F. 180 Library of Congress Cataloging-in-Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask / Patricia F.
    [Show full text]
  • The Antigonids and the Ruler Cult. Global and Local Perspectives?
    The Antigonids and the Ruler Cult Global and Local Perspectives? 1 Franca Landucci DOI – 10.7358/erga-2016-002-land AbsTRACT – Demetrius Poliorketes is considered by modern scholars the true founder of ruler cult. In particular the Athenians attributed him several divine honors between 307 and 290 BC. The ancient authors in general consider these honors in a negative perspec- tive, while offering words of appreciation about an ideal sovereignty intended as a glorious form of servitude and embodied in Antigonus Gonatas, Demetrius Poliorketes’ son and heir. An analysis of the epigraphic evidences referring to this king leads to the conclusion that Antigonus Gonatas did not officially encourage the worship towards himself. KEYWORDS – Antigonids, Antigonus Gonatas, Demetrius Poliorketes, Hellenism, ruler cult. Antigonidi, Antigono Gonata, culto del sovrano, Demetrio Poliorcete, ellenismo. Modern scholars consider Demetrius Poliorketes the true founder of ruler cult due to the impressively vast literary tradition on the divine honours bestowed upon this historical figure, especially by Athens, between the late fourth and the early third century BC 2. As evidenced also in modern bib- liography, these honours seem to climax in the celebration of Poliorketes as deus praesens in the well-known ithyphallus dedicated to him by the Athenians around 290 3. Documentation is however pervaded by a tone that is strongly hostile to the granting of such honours. Furthermore, despite the fact that it has been handed down to us through Roman Imperial writers like Diodorus, Plutarch and Athenaeus, the tradition reflects a tendency contemporary to the age of the Diadochi, since these same authors refer, often explicitly, to a 1 All dates are BC, unless otherwise stated.
    [Show full text]
  • Central Balkans Cradle of Aegean Culture
    ANTONIJE SHKOKLJEV SLAVE NIKOLOVSKI - KATIN PREHISTORY CENTRAL BALKANS CRADLE OF AEGEAN CULTURE Prehistory - Central Balkans Cradle of Aegean culture By Antonije Shkokljev Slave Nikolovski – Katin Translated from Macedonian to English and edited By Risto Stefov Prehistory - Central Balkans Cradle of Aegean culture Published by: Risto Stefov Publications [email protected] Toronto, Canada All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage and retrieval system without written consent from the author, except for the inclusion of brief and documented quotations in a review. Copyright 2013 by Antonije Shkokljev, Slave Nikolovski – Katin & Risto Stefov e-book edition 2 Index Index........................................................................................................3 COMMON HISTORY AND FUTURE ..................................................5 I - GEOGRAPHICAL CONFIGURATION OF THE BALKANS.........8 II - ARCHAEOLOGICAL DISCOVERIES .........................................10 III - EPISTEMOLOGY OF THE PANNONIAN ONOMASTICS.......11 IV - DEVELOPMENT OF PALEOGRAPHY IN THE BALKANS....33 V – THRACE ........................................................................................37 VI – PREHISTORIC MACEDONIA....................................................41 VII - THESSALY - PREHISTORIC AEOLIA.....................................62 VIII – EPIRUS – PELASGIAN TESPROTIA......................................69
    [Show full text]
  • The Great City
    Morandi Bonacossi (eds) Bonacossi Morandi & Petit NINEVEH, THE GREAT CITY ‘Well, as for Nineveh, skipper, it was wiped out long ago. There’s not a trace of it left, and one can’t even guess where it was’ (Lucian, 2nd century AD). Nineveh, the once-flourishing capital of the Assyrian Empire, has fascinated writers, travellers and historians alike since its complete annihilation by allied forces in 612 BC. It was said to have been a great and populous city with 90-km walls, stunning palaces and colossal statues of pure gold. Since 1842 archaeologists have been investigating CITY GREAT THE NINEVEH, the ruins of Nineveh, which are located on the eastern banks of the river Tigris, near the modern Iraqi city of Mosul. The hundreds of thousands of objects that have been collected tell an intriguing story of life and death in a remarkable Mesopotamian city. The edited volume Nineveh, the Great City contains more than 65 articles by international specialists, providing the reader with a detailed and thorough study of the site of Nineveh. It describes the history of the city, the excavations and the dispersed material culture that can today be appreciated in more than 100 museums and institutes around the world. Special attention is paid to the endangered heritage of Nineveh, which recently faced destruction for the second time in its history. This lavishly illustrated volume is intended to appeal to readers interested NINEVEH in culture and heritage, as well as to students and professional academics. THE GREAT CITY Symbol of Beauty and Power edited by L.P.
    [Show full text]
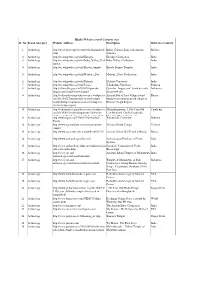
  • 2.Hindu Websites Sorted Category Wise
    Hindu Websites sorted Category wise Sl. No. Broad catergory Website Address Description Reference Country 1 Archaelogy http://aryaculture.tripod.com/vedicdharma/id10. India's Cultural Link with Ancient Mexico html America 2 Archaelogy http://en.wikipedia.org/wiki/Harappa Harappa Civilisation India 3 Archaelogy http://en.wikipedia.org/wiki/Indus_Valley_Civil Indus Valley Civilisation India ization 4 Archaelogy http://en.wikipedia.org/wiki/Kiradu_temples Kiradu Barmer Temples India 5 Archaelogy http://en.wikipedia.org/wiki/Mohenjo_Daro Mohenjo_Daro Civilisation India 6 Archaelogy http://en.wikipedia.org/wiki/Nalanda Nalanda University India 7 Archaelogy http://en.wikipedia.org/wiki/Taxila Takshashila University Pakistan 8 Archaelogy http://selians.blogspot.in/2010/01/ganesha- Ganesha, ‘lingga yoni’ found at newly Indonesia lingga-yoni-found-at-newly.html discovered site 9 Archaelogy http://vedicarcheologicaldiscoveries.wordpress.c Ancient Idol of Lord Vishnu found Russia om/2012/05/27/ancient-idol-of-lord-vishnu- during excavation in an old village in found-during-excavation-in-an-old-village-in- Russia’s Volga Region russias-volga-region/ 10 Archaelogy http://vedicarcheologicaldiscoveries.wordpress.c Mahendraparvata, 1,200-Year-Old Cambodia om/2013/06/15/mahendraparvata-1200-year- Lost Medieval City In Cambodia, old-lost-medieval-city-in-cambodia-unearthed- Unearthed By Archaeologists 11 Archaelogy http://wikimapia.org/7359843/Takshashila- Takshashila University Pakistan Taxila 12 Archaelogy http://www.agamahindu.com/vietnam-hindu- Vietnam
    [Show full text]
  • University Microfilms, Inc., Ann Arbor, Michigan LINDA JANE PIPER 1967
    This dissertation has been microfilmed exactly as received 66-15,122 PIPER, Linda Jane, 1935- A HISTORY OF SPARTA: 323-146 B.C. The Ohio State University, Ph.D., 1966 History, ancient University Microfilms, Inc., Ann Arbor, Michigan LINDA JANE PIPER 1967 All Rights Reserved A HISTORY OF SPARTA: 323-1^6 B.C. DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Linda Jane Piper, A.B., M.A. The Ohio State University 1966 Approved by Adviser Department of History PREFACE The history of Sparta from the death of Alexander in 323 B.C; to the destruction of Corinth in 1^6 B.C. is the history of social revolution and Sparta's second rise to military promi­ nence in the Peloponnesus; the history of kings and tyrants; the history of Sparta's struggle to remain autonomous in a period of amalgamation. It is also a period in Sparta's history too often neglected by historians both past and present. There is no monograph directly concerned with Hellenistic Sparta. For the most part, this period is briefly and only inci­ dentally covered in works dealing either with the whole history of ancient Sparta, or simply as a part of Hellenic or Hellenistic 1 2 history in toto. Both Pierre Roussel and Eug&ne Cavaignac, in their respective surveys of Spartan history, have written clear and concise chapters on the Hellenistic period. Because of the scope of their subject, however, they were forced to limit them­ selves to only the most important events and people of this time, and great gaps are left in between.
    [Show full text]
  • Proquest Dissertations
    INFORMATION TO USERS This manuscript has been reproduced from the microfilm master UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print t>leedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6’ x 9” black arxf white photographic prints are available for any pfiotographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. Bell & Howell Information and Learning 300 North Zeeb Road, Ann Arbor, Ml 48106-1346 USA 800-521-0600 UMI TRADE IN THE EASTERN MEDITERRANEAN, 100-700 AD: THE CERAMIC EVIDENCE DISSERTATION Presented in Partial Fulfillment of the Requirements for The Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Robert Scott Moore, M.A., B.A. The Ohio State University 2000 Dissertation Committee: Approved by Professor Timothy E.
    [Show full text]
  • Religion and Reconciliation in Greek Cities (2010)
    Religion and Reconciliation in Greek Cities AMERICAN PHILOLOGICAL ASSOCIATION american classical studies volume 54 Series Editor Kathryn J. Gutzwiller Studies in Classical History and Society Meyer Reinhold Sextus Empiricus The Transmission and Recovery of Pyrrhonism Luciano Floridi The Augustan Succession An Historical Commentary on Cassius Dio’s Roman History Books 55 56 (9 B.C. A.D. 14) Peter Michael Swan Greek Mythography in the Roman World Alan Cameron Virgil Recomposed The Mythological and Secular Centos in Antiquity Scott McGill Representing Agrippina Constructions of Female Power in the Early Roman Empire Judith Ginsburg Figuring Genre in Roman Satire Catherine Keane Homer’s Cosmic Fabrication Choice and Design in the Iliad Bruce Heiden Hyperides Funeral Oration Judson Herrman Religion and Reconciliation in Greek Cities The Sacred Laws of Selinus and Cyrene Noel Robertson Religion and Reconciliation in Greek Cities The Sacred Laws of Selinus and Cyrene NOEL ROBERTSON 1 2010 3 Oxford University Press, Inc., publishes works that further Oxford University’s objective of excellence in research, scholarship, and education. Oxford New York Auckland Cape Town Dar es Salaam Hong Kong Karachi Kuala Lumpur Madrid Melbourne Mexico City Nairobi New Delhi Shanghai Taipei Toronto With offices in Argentina Austria Brazil Chile Czech Republic France Greece Guatemala Hungary Italy Japan Poland Portugal Singapore South Korea Switzerland Thailand Turkey Ukraine Vietnam Copyright q 2010 by the American Philological Association Published by Oxford University Press, Inc. 198 Madison Avenue, New York, New York 10016 www.oup.com Oxford is a registered trademark of Oxford University Press. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of Oxford University Press.
    [Show full text]
  • Download PDF Datastream
    A Dividing Sea The Adriatic World from the Fourth to the First Centuries BC By Keith Robert Fairbank, Jr. B.A. Brigham Young University, 2010 M.A. Brigham Young University, 2012 Submitted in partial fulfillment of the requirements for the Degree of Doctor of Philosophy in the Program in Ancient History at Brown University PROVIDENCE, RHODE ISLAND MAY 2018 © Copyright 2018 by Keith R. Fairbank, Jr. This dissertation by Keith R. Fairbank, Jr. is accepted in its present form by the Program in Ancient History as satisfying the dissertation requirement for the degree of Doctor of Philosophy. Date _______________ ____________________________________ Graham Oliver, Advisor Recommended to the Graduate Council Date _______________ ____________________________________ Peter van Dommelen, Reader Date _______________ ____________________________________ Lisa Mignone, Reader Approved by the Graduate Council Date _______________ ____________________________________ Andrew G. Campbell, Dean of the Graduate School iii CURRICULUM VITAE Keith Robert Fairbank, Jr. hails from the great states of New York and Montana. He grew up feeding cattle under the Big Sky, serving as senior class president and continuing on to Brigham Young University in Utah for his BA in Humanities and Classics (2010). Keith worked as a volunteer missionary for two years in Brazil, where he learned Portuguese (2004–2006). Keith furthered his education at Brigham Young University, earning an MA in Classics (2012). While there he developed a curriculum for accelerated first year Latin focused on competency- based learning. He matriculated at Brown University in fall 2012 in the Program in Ancient History. While at Brown, Keith published an appendix in The Landmark Caesar. He also co- directed a Mellon Graduate Student Workshop on colonial entanglements.
    [Show full text]