DOCSLIB.ORG

Discrete Cosine Transform Based Image Fusion Techniques VPS Naidu MSDF Lab, FMCD, National Aerospace Laboratories, Bangalore, INDIA E.Mail: [email protected]

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Cosine Transform Based Image Fusion Techniques VPS Naidu MSDF Lab, FMCD, National Aerospace Laboratories, Bangalore, INDIA E.Mail: Vpsnaidu@Gmail.Com View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NAL-IR Journal of Communication, Navigation and Signal Processing (January 2012) Vol. 1, No. 1, pp. 35-45 Discrete Cosine Transform based Image Fusion Techniques VPS Naidu MSDF Lab, FMCD, National Aerospace Laboratories, Bangalore, INDIA E.mail: [email protected] Abstract: Six different types of image fusion algorithms based on 1 discrete cosine transform (DCT) were developed and their , k 1 0 performance was evaluated. Fusion performance is not good while N Where (k ) 1 and using the algorithms with block size less than 8x8 and also the block 1 2 size equivalent to the image size itself. DCTe and DCTmx based , 1 k 1 N 1 1 image fusion algorithms performed well. These algorithms are very N 1 simple and might be suitable for real time applications. 1 , k 0 Keywords: DCT, Contrast measure, Image fusion 2 N 2 (k 1 ) I. INTRODUCTION 2 , 1 k 2 N 2 1 Off late, different image fusion algorithms have been developed N 2 to merge the multiple images into a single image that contain all useful information. Pixel averaging of the source images k 1 & k 2 discrete frequency variables (n1 , n 2 ) pixel index (the images to be fused) is the simplest image fusion technique and it often produces undesirable side effects in the fused image Similarly, the 2D inverse discrete cosine transform is defined including reduced contrast. To overcome this side effects many as: researchers have developed multi resolution [1-3], multi scale [4,5] and statistical signal processing [6,7] based image fusion x(n1 , n 2 ) (k 1 ) (k 2 ) N 1 N 1 techniques. 1 2 (2n1 1)k 1 In similar line, contrast based image fusion algorithm in (k 1 ) (k 2 ) X (k 1 , k 2 ) cos k 0 k 0 2 N DCT domain has been presented [8] to fuse the out of focus 1 2 1 images. Local contrast is measured by 8x8 blocks. However, (2n 1)k 0 n1 N 1 1 there is no discussion on the fusion performance by choosing cos 2 2 , 2 N 0 n N 1 different block sizes. The present paper presents six different 2 2 2 (2) DCT based image fusion techniques and studies their performance. III. CONTRAST MEASURE II. DISCRETE COSINE TRANSFORM DCT decomposes the image/block into a series of waveforms, Discrete cosine transform (DCT) is an important transform each with a particular frequency. DCT coefficients are extensively used in digital image processing. Large DCT segregated into 21N different frequency bands for image or coefficients are concentrated in the low frequency region; th block of size NxN . The m band is composed of the hence, it is known to have excellent energy compactness properties [9-11]. The 2D discrete cosine transform coefficients with m k12 k . The contrast measure at each X (k 1 , k 2 ) of an image or 2D signal x(n1 , n 2 ) of size coefficient in the band is computed as [15-17]: N xN is defined as [12-14]: 1 2 X ( k , k ) C ( k , k ) 12 12 m 1 X (k 1 , k 2 ) (k 1 ) (k 2 ) E j N 1 1 N 2 1 j 0 (2n1 1)k 1 (3) x(n1 , n 2 ) cos 2 N (1) n1 0 n 2 0 1 X ( p,t ) 0 k N 1 Where j t p and j1 j N (2n 2 1)k 2 1 1 E j Y cos , Y 2( N 1 ) j 1 j N 2 N 2 0 k 2 N 2 1 (4) th E j is the average amplitude over a j spectral band. The DCT output for image or block size of 8x8 is shown in Fig-1. It also illustrates the 1st and 5th bands (enclosed with rectangles). VPS Naidu DCT av: In this fusion rule, all DCT coefficients from both E image blocks are averaged to get fused DCT coefficients. It is E1 5 X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)00 01 02 03 04 05 06 07 very simple and basic image fusion technique in DCT domain. X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)10 11 12 13 14 15 16 17 X(k,kf 1 2 )05 . X(k,k1 1 2 ) X(k,k 2 1 2 ) (5) X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)20 21 22 23 24 25 26 27 Where k,k12 0 ,, 1 2 ,...,N 1 X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)30 31 32 33 34 35 36 37 X DCTma: The DC components from both image blocks are X(,)40 X(,)X(,)X(,)X(,)X(,)X(,)X(,)41 42 43 44 45 46 47 averaged. The largest magnitude AC coefficients are chosen, since the detailed coeficients correspond to sharper brightness X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)50 51 52 53 54 55 56 57 changes in the images such as edges and object boundaries etc. These coeficients are fluctuating around zero. X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)60 61 62 63 64 65 66 67 X(,).X(,)X(,)0 0 0 5 0 0 0 0 X(,)X(,)X(,)X(,)X(,)X(,)X(,)X(,)70 71 72 73 74 75 76 77 f 12 (6a) X(k,k) X(k,k) X(k,k) Fig-1 DCT output of an image or a bock size of 8x8 1 1 2 1 1 2 2 1 2 X ( k ,k ) f 12 X(k,k) X(k,k) X(k,k) IV. IMAGE FUSION 2 1 2 1 1 2 2 1 2 (6b) Six different types of image fusion techniques using DCT are Where k,k1 , 2 , 3 ,...,N 1 12 presented in this section. Image to be fused are divided into non-overlapping blocks of size NxN as shown in Fig-2. DCT DCTah: The lowest AC components including DC coefficients coefficients are computed for each block and fusion rules are are averaged and the remaining AC coefficients are chosen applied to get fused DCT coefficients. IDCT is then applied on based on largest magnitude. the fused coefficients to produce the fused image/block. The procedure is repeated for each block. X(k,kf 1 2 )05 . X(k,k1 1 2 ) X(k,k 2 1 2 ) (7a) Where k,k12 0 ,,,...,.N 1 2 0 5 1 CT (7b) Where k,k0 .N,. 5 0 5 1 ,.N 0 5 2 ,...,N 1 12 T DCTcm: The DC coefficients are averaged and the AC coefficients are chosen based on largest contrast measure. CT (8a) X(k,k1 1 2 ) C(k,k 1 1 2 ) C(k,k 2 1 2 ) Xf ( k12 ,k ) X(k,k2 1 2 ) C(k,k 1 1 2 ) C(k,k 2 1 2 ) (8b) Fig-2 Framework of DCT based image fusion algorithm Where k,k12 1 , 2 , 3 ,...,N 1 The following fusion rules are used in image fusion process. DCTch: It is very much similar to DCT ah. The lowest AC components including DC coefficients are averaged and the Let the X1 be the DCT coefficients of image block from image remaining AC coefficients are chosen based on largest contrast I1 and similarly let the X 2 be the DCT coefficients of image measure. block from image I . Assume the image block is of size 2 (9a) NxN and X f be the fused DCT coefficients. Where 36 Discrete Cosine Transform based Image Fusion Techniques X(k,k1 1 2 ) C(k,k 1 1 2 ) C(k,k 2 1 2 ) 2 : Variance of Xf ( k12 ,k ) It X(k,k ) C(k,k ) C(k,k ) 2 1 2 1 1 2 2 1 2 (9b) 2 : Variance of If Where If : Covariance of and DCTe: It is similar to DCTcm. DC components are averaged IItf together. AC coefficients correspond to the frequency band 2 2 having largest energy is chosen. c1 (0 . 01 L ) and c3 (0 . 03 L ) are the constants to stabilize the division with weak denominator (10a) X1 ( k 1 , k 2 ) Ejj 1 E 2 When the ground truth image is not available, the following metrics can be used to evaluate the proposed six fusion Xf ( k12 , k ) algorithms. X2 ( k 1 , k 2 ) Ejj 1 E 2 (10b) X(,).X(,)X(,)f 10. 0Spatial 0 5 Frequency12 0 0 [6,21] 0 0 Where and j k12 k The frequency in spatial domain indicates the overall activity level in the fused image and it is computed as V. FUSION EVALUATION METRICS Row frequency: MN11 1 2 (13a) The following fusion evaluation metrics are used to evaluate RF I(i,j)I(i,jff1 ) MN the performance of the developed six image fusion algorithms. ij01 When the ground truth image is available: Column frequency: NM11 1. Peak Signal to Noise Ratio (PSNR) [3,6,18] 1 2 (13b) CF I(i,j)I(iff1 ,j) PSNR value will be high when the fused and the ground MN ji01 truth images are comparable. Higher value implies better fusion. The peak signal to noise ratio is computed as: Spatial frequency: SF RF 2 CF 2 (14) The fused image with high SF would be considered. 2 L PSNR 20 log (11) 10 M N 2. Fusion quality index [22] 1 2 The range of this metric is 0 to 1. One indicates the fused image I r (i, j) I f (i, j) MN i 1 j 1 containsk,k 12all the information0 .N,.
Load more

Recommended publications
  • Digital Signals
    Technical Information Digital Signals 1 1 bit t Part 1 Fundamentals Technical Information Part 1: Fundamentals Part 2: Self-operated Regulators Part 3: Control Valves Part 4: Communication Part 5: Building Automation Part 6: Process Automation Should you have any further questions or suggestions, please do not hesitate to contact us: SAMSON AG Phone (+49 69) 4 00 94 67 V74 / Schulung Telefax (+49 69) 4 00 97 16 Weismüllerstraße 3 E-Mail: [email protected] D-60314 Frankfurt Internet: http://www.samson.de Part 1 ⋅ L150EN Digital Signals Range of values and discretization . 5 Bits and bytes in hexadecimal notation. 7 Digital encoding of information. 8 Advantages of digital signal processing . 10 High interference immunity. 10 Short-time and permanent storage . 11 Flexible processing . 11 Various transmission options . 11 Transmission of digital signals . 12 Bit-parallel transmission. 12 Bit-serial transmission . 12 Appendix A1: Additional Literature. 14 99/12 ⋅ SAMSON AG CONTENTS 3 Fundamentals ⋅ Digital Signals V74/ DKE ⋅ SAMSON AG 4 Part 1 ⋅ L150EN Digital Signals In electronic signal and information processing and transmission, digital technology is increasingly being used because, in various applications, digi- tal signal transmission has many advantages over analog signal transmis- sion. Numerous and very successful applications of digital technology include the continuously growing number of PCs, the communication net- work ISDN as well as the increasing use of digital control stations (Direct Di- gital Control: DDC). Unlike analog technology which uses continuous signals, digital technology continuous or encodes the information into discrete signal states (Fig. 1). When only two discrete signals states are assigned per digital signal, these signals are termed binary si- gnals.
    [Show full text]
  • How I Came up with the Discrete Cosine Transform Nasir Ahmed Electrical and Computer Engineering Department, University of New Mexico, Albuquerque, New Mexico 87131
    mxT*L. BImL4L. PRocEsSlNG 1,4-5 (1991) How I Came Up with the Discrete Cosine Transform Nasir Ahmed Electrical and Computer Engineering Department, University of New Mexico, Albuquerque, New Mexico 87131 During the late sixties and early seventies, there to study a “cosine transform” using Chebyshev poly- was a great deal of research activity related to digital nomials of the form orthogonal transforms and their use for image data compression. As such, there were a large number of T,(m) = (l/N)‘/“, m = 1, 2, . , N transforms being introduced with claims of better per- formance relative to others transforms. Such compari- em- lh) h = 1 2 N T,(m) = (2/N)‘%os 2N t ,...) . sons were typically made on a qualitative basis, by viewing a set of “standard” images that had been sub- jected to data compression using transform coding The motivation for looking into such “cosine func- techniques. At the same time, a number of researchers tions” was that they closely resembled KLT basis were doing some excellent work on making compari- functions for a range of values of the correlation coef- sons on a quantitative basis. In particular, researchers ficient p (in the covariance matrix). Further, this at the University of Southern California’s Image Pro- range of values for p was relevant to image data per- cessing Institute (Bill Pratt, Harry Andrews, Ali Ha- taining to a variety of applications. bibi, and others) and the University of California at Much to my disappointment, NSF did not fund the Los Angeles (Judea Pearl) played a key role.
    [Show full text]
  • Temperature Compensation Circuit for ISFET Sensor
    Journal of Low Power Electronics and Applications Article Temperature Compensation Circuit for ISFET Sensor Ahmed Gaddour 1,2,* , Wael Dghais 2,3, Belgacem Hamdi 2,3 and Mounir Ben Ali 3,4 1 National Engineering School of Monastir (ENIM), University of Monastir, Monastir 5000, Tunisia 2 Electronics and Microelectronics Laboratory, LR99ES30, Faculty of Sciences of Monastir, University of Monastir, Monastir 5000, Tunisia; [email protected] (W.D.); [email protected] (B.H.) 3 Higher Institute of Applied Sciences and Technology of Sousse (ISSATSo), University of Sousse, Sousse 4003, Tunisia; [email protected] 4 Nanomaterials, Microsystems for Health, Environment and Energy Laboratory, LR16CRMN01, Centre for Research on Microelectronics and Nanotechnology, Sousse 4034, Tunisia * Correspondence: [email protected]; Tel.: +216-50998008 Received: 3 November 2019; Accepted: 21 December 2019; Published: 4 January 2020 Abstract: PH measurements are widely used in agriculture, biomedical engineering, the food industry, environmental studies, etc. Several healthcare and biomedical research studies have reported that all aqueous samples have their pH tested at some point in their lifecycle for evaluation of the diagnosis of diseases or susceptibility, wound healing, cellular internalization, etc. The ion-sensitive field effect transistor (ISFET) is capable of pH measurements. Such use of the ISFET has become popular, as it allows sensing, preprocessing, and computational circuitry to be encapsulated on a single chip, enabling miniaturization and portability. However, the extracted data from the sensor have been affected by the variation of the temperature. This paper presents a new integrated circuit that can enhance the immunity of ion-sensitive field effect transistors (ISFET) against the temperature.
    [Show full text]
  • Reception Performance Improvement of AM/FM Tuner by Digital Signal Processing Technology
    Reception performance improvement of AM/FM tuner by digital signal processing technology Akira Hatakeyama Osamu Keishima Kiyotaka Nakagawa Yoshiaki Inoue Takehiro Sakai Hirokazu Matsunaga Abstract With developments in digital technology, CDs, MDs, DVDs, HDDs and digital media have become the mainstream of car AV products. In terms of broadcasting media, various types of digital broadcasting have begun in countries all over the world. Thus, there is a demand for smaller and thinner products, in order to enhance radio performance and to achieve consolidation with the above-mentioned digital media in limited space. Due to these circumstances, we are attaining such performance enhancement through digital signal processing for AM/FM IF and beyond, and both tuner miniaturization and lighter products have been realized. The digital signal processing tuner which we will introduce was developed with Freescale Semiconductor, Inc. for the 2005 line model. In this paper, we explain regarding the function outline, characteristics, and main tech- nology involved. 22 Reception performance improvement of AM/FM tuner by digital signal processing technology Introduction1. Introduction from IF signals, interference and noise prevention perfor- 1 mance have surpassed those of analog systems. In recent years, CDs, MDs, DVDs, and digital media have become the mainstream in the car AV market. 2.2 Goals of digitalization In terms of broadcast media, with terrestrial digital The following items were the goals in the develop- TV and audio broadcasting, and satellite broadcasting ment of this digital processing platform for radio: having begun in Japan, while overseas DAB (digital audio ①Improvements in performance (differentiation with broadcasting) is used mainly in Europe and SDARS (satel- other companies through software algorithms) lite digital audio radio service) and IBOC (in band on ・Reduction in noise (improvements in AM/FM noise channel) are used in the United States, digital broadcast- reduction performance, and FM multi-pass perfor- ing is expected to increase in the future.
    [Show full text]
  • Next-Generation Photonic Transport Network Using Digital Signal Processing
    Next-Generation Photonic Transport Network Using Digital Signal Processing Yasuhiko Aoki Hisao Nakashima Shoichiro Oda Paparao Palacharla Coherent optical-fiber transmission technology using digital signal processing is being actively researched and developed for use in transmitting high-speed signals of the 100-Gb/s class over long distances. It is expected that network capacity can be further expanded by operating a flexible photonic network having high spectral efficiency achieved by applying an optimal modulation format and signal processing algorithm depending on the transmission distance and required bit rate between transmit and receive nodes. A system that uses such adaptive modulation technology should be able to assign in real time a transmission path between a transmitter and receiver. Furthermore, in the research and development stage, optical transmission characteristics for each modulation format and signal processing algorithm to be used by the system should be evaluated under emulated quasi-field conditions. We first discuss how the use of transmitters and receivers supporting multiple modulation formats can affect network capacity. We then introduce an evaluation platform consisting of a coherent receiver based on a field programmable gate array (FPGA) and polarization mode dispersion/polarization dependent loss (PMD/PDL) emulators with a recirculating-loop experimental system. Finally, we report the results of using this platform to evaluate the transmission characteristics of 112-Gb/s dual-polarization, quadrature phase shift keying (DP-QPSK) signals by emulating the factors that degrade signal transmission in a real environment. 1. Introduction amplifiers—which is becoming a limiting factor In the field of optical communications in system capacity—can be efficiently used.
    [Show full text]
  • Digital Signal Processing: Theory and Practice, Hardware and Software
    AC 2009-959: DIGITAL SIGNAL PROCESSING: THEORY AND PRACTICE, HARDWARE AND SOFTWARE Wei PAN, Idaho State University Wei Pan is Assistant Professor and Director of VLSI Laboratory, Electrical Engineering Department, Idaho State University. She has several years of industrial experience including Siemens (project engineering/management.) Dr. Pan is an active member of ASEE and IEEE and serves on the membership committee of the IEEE Education Society. S. Hossein Mousavinezhad, Idaho State University S. Hossein Mousavinezhad is Professor and Chair, Electrical Engineering Department, Idaho State University. Dr. Mousavinezhad is active in ASEE and IEEE and is an ABET program evaluator. Hossein is the founding general chair of the IEEE International Conferences on Electro Information Technology. Kenyon Hart, Idaho State University Kenyon Hart is Specialist Engineer and Associate Lecturer, Electrical Engineering Department, Idaho State University, Pocatello, Idaho. Page 14.491.1 Page © American Society for Engineering Education, 2009 Digital Signal Processing, Theory/Practice, HW/SW Abstract Digital Signal Processing (DSP) is a course offered by many Electrical and Computer Engineering (ECE) programs. In our school we offer a senior-level, first-year graduate course with both lecture and laboratory sections. Our experience has shown that some students consider the subject matter to be too theoretical, relying heavily on mathematical concepts and abstraction. There are several visible applications of DSP including: cellular communication systems, digital image processing and biomedical signal processing. Authors have incorporated many examples utilizing software packages including MATLAB/MATHCAD in the course and also used classroom demonstrations to help students visualize some difficult (but important) concepts such as digital filters and their design, various signal transformations, convolution, difference equations modeling, signals/systems classifications and power spectral estimation as well as optimal filters.
    [Show full text]
  • A Novel MEMS Pressure Sensor with MOSFET on Chip
    A Novel MEMS Pressure Sensor with MOSFET on Chip Zhao-Hua Zhang *, Yan-Hong Zhang, Li-Tian Liu, Tian-Ling Ren Tsinghua National Laboratory for Information Science and Technology Institute of Microelectronics, Tsinghua University Beijing 100084, China [email protected] Abstract—A novel MOSFET pressure sensor was proposed Figure 1. Two PMOSFET’s and two piezoresistors are based on the MOSFET stress sensitive phenomenon, in which connected to form a Wheatstone bridge. To obtain the the source-drain current changes with the stress in channel maximum sensitivity, these components are placed near the region. Two MOSFET’s and two piezoresistors were employed four sides of the silicon diaphragm, which are the high stress to form a Wheatstone bridge served as sensitive unit in the regions. The MOSFET’s has the same structure parameter novel sensor. Compared with the traditional piezoresistive W/L, same threshold voltage VT and gate-source voltage VGS pressure sensor, this MOSFET sensor’s sensitivity is improved (equal to VG-Vdd). They are designed to work in the significantly, meanwhile the power consumption can be saturation region. The piezoresistors also have the same decreased. The fabrication of the novel pressure sensor is low- resistance R . cost and compatible with standard IC process. It shows the 0 great promising application of MOSFET-bridge-circuit structure for the high performance pressure sensor. This kind of MEMS pressure sensor with signal process circuit on the same chip can be used in positive or negative Tire Pressure Monitoring System (TPMS) which is very hot in automotive electron research field. I.
    [Show full text]
  • Simplifying Current Sensing (Rev. A)
    Simplifying Current Sensing How to design with current sense amplifiers Table of contents Introduction . 3 Chapter 4: Integrating the current-sensing signal chain Chapter 1: Current-sensing overview Integrating the current-sensing signal path . 40 Integrating the current-sense resistor . 42 How integrated-resistor current sensors simplify Integrated, current-sensing PCB designs . 4 analog-to-digital converter . 45 Shunt-based current-sensing solutions for BMS Enabling Precision Current Sensing Designs with applications in HEVs and EVs . 6 Non-Ratiometric Magnetic Current Sensors . 48 Common uses for multichannel current monitoring . 9 Power and energy monitoring with digital Chapter 5: Wide VIN and isolated current sensors . 11 current measurement 12-V Battery Monitoring in an Automotive Module . 14 Simplifying voltage and current measurements in Interfacing a differential-output (isolated) amplifier battery test equipment . 17 to a single-ended-input ADC . 50 Extending beyond the maximum common-mode range of discrete current-sense amplifiers . 52 Chapter 2: Out-of-range current measurements Low-Drift, Precision, In-Line Isolated Magnetic Motor Current Measurements . 55 Measuring current to detect out-of-range conditions . 20 Monitoring current for multiple out-of-range Authors: conditions . 22 Scott Hill, Dennis Hudgins, Arjun Prakash, Greg Hupp, High-side motor current monitoring for overcurrent protection . 25 Scott Vestal, Alex Smith, Leaphar Castro, Kevin Zhang, Maka Luo, Raphael Puzio, Kurt Eckles, Guang Zhou, Chapter 3: Current sensing in Stephen Loveless, Peter Iliya switching systems Low-drift, precision, in-line motor current measurements with enhanced PWM rejection . 28 High-side drive, high-side solenoid monitor with PWM rejection . 30 Current-mode control in switching power supplies .
    [Show full text]
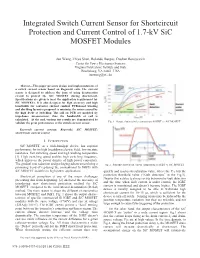
  • Integrated Switch Current Sensor for Shortcircuit Protection and Current Control of 1.7-Kv Sic MOSFET Modules
    Integrated Switch Current Sensor for Shortcircuit Protection and Current Control of 1.7-kV SiC MOSFET Modules Jun Wang, Zhiyu Shen, Rolando Burgos, Dushan Boroyevich Center for Power Electronics Systems Virginia Polytechnic Institute and State Blacksburg, VA 24061, USA [email protected] Abstract—This paper presents design and implementations of a switch current sensor based on Rogowski coils. The current sensor is designed to address the issue of using desaturation circuit to protect the SiC MOSFET during shortcircuit. Specifications are given to meet the application requirement for SiC MOSFETs. It is also designed for high accuracy and high bandwidth for converter current control. PCB-based winding and shielding layout is proposed to minimize the noises caused by the high dv/dt at switching. The coil on PCB are modeled by impedance measurement, thus the bandwidth of coil is calculated. At the end, various test results are demonstrated to validate the great performance of the switch current sensor. Fig. 1. Output characteristics comparison: Si IGBT vs. SiC MOSFET Keywords—current sensing; Rogowski; SiC MOSFET; shortcircuit; current control I. INTRODUCTION SiC MOSFET, as a wide-bandgap device, has superior performance for its high breakdown electric field, low on-state resistance, fast switching speed and high working temperature [1]. High switching speed enables high switching frequency, which improves the power density of high power converters. The gradual cost reduction and packaging advancement bring a Fig. 2. Principle shortcircuit current comparison: Si IGBT vs. SiC MOSFET promising trend of replacing the conventional Si IGBTs with SiC MOSFET modules in high power applications. quickly and reaches its saturation value, where the VCE hits the Shortcircuit protection is one of the major challenges protection threshold value (“Fault detection” in the Fig.1).
    [Show full text]
  • Development of MEMS Capacitive Sensor Using a MOSFET Structure
    Extended Summary 本文は pp.102-107 Development of MEMS Capacitive Sensor Using a MOSFET Structure Hayato Izumi Non-member (Kansai University, [email protected]) Yohei Matsumoto Non-member (Kansai University, [email protected] u.ac.jp) Seiji Aoyagi Member (Kansai University, [email protected] u.ac.jp) Yusaku Harada Non-member (Kansai University, [email protected] u.ac.jp) Shoso Shingubara Non-member (Kansai University, [email protected]) Minoru Sasaki Member (Toyota Technological Institute, [email protected]) Kazuhiro Hane Member (Tohoku University, [email protected]) Hiroshi Tokunaga Non-member (M. T. C. Corp., [email protected]) Keywords : MOSFET, capacitive sensor, accelerometer, circuit for temperature compensation The concept of a capacitive MOSFET sensor for detecting voltage change, is proposed (Fig. 4). This circuitry is effective for vertical force applied to its floating gate was already reported by compensating ambient temperature, since two MOSFETs are the authors (Fig. 1). This sensor detects the displacement of the simultaneously suffer almost the same temperature change. The movable gate electrode from changes in drain current, and this performance of this circuitry is confirmed by SPICE simulation. current can be amplified electrically by adding voltage to the gate, The operating point, i.e., the output voltage, is stable irrespective i.e., the MOSFET itself serves as a mechanical sensor structure. of the ambient temperature change (Fig. 5(a)). The output voltage Following this, in the present paper, a practical test device is has comparatively good linearity to the gap length, which would fabricated.
    [Show full text]
  • THE IMPACT QF MOSFET-BASED SENSORS * Abstract The
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Universiteit Twente Repository Sensors and Actuators, 8 (1985) 109 - 127 109 THE IMPACT QF MOSFET-BASED SENSORS * P BERGVELD Department of Electrical Engmeermg, Twente Unwerslty of Technology, P 0 Box 217, 7500 AE Enschede (The Netherlands) (Received May 21,1985, m revlsed form October 4,1985, accepted October 29, 1985) Abstract The basic structure as well as the physical existence of the MOS held- effect transistor 1s without doubt of great importance for the development of a whole series of sensors for the measurement of physical and chemical environmental parameters The equation for the MOSFET dram current already shows a number of parameters that can be directly influenced by an external quantity, but small technological varlatlons of the orlgmal MOSFET configuration also give rise to a large number of sensing propertles All devices have m common that a surface charge 1s measured m a slllcon chip, depending on an electric field m the adJacent insulator FET-based sensors such as the GASFET, OGFET, ADFET, SAFET, CFT, PRESSFET, ISFET, CHEMFET, REFET, ENFET, IMFET, BIOFET, etc developed up to the present or those to be developed m the near future will be discussed m relation to the conslderatlons mentioned above 1. Introduction The measurement of semiconductor surface charge as a function of an electric field perpendicular to the surface was mentloned as early as 1925 by Llhenfeld and Hell as a possible principle for an electronic device that would not consume any power
    [Show full text]
  • Multiplexing and Sampling Theory
    Multiplexing and Sampling Theory THE ECONOMY OF MULTIPLEXING contact type determine its current carrying capacity. For instance, laboratory instrument relays typically switch Sampled-Data Systems up to 3A, while industrial applications use larger relays An ideal data acquisition system uses a single ADC for to switch higher currents, often 5 to 10A. each measurement channel. In this way, all data are captured in parallel and events in each channel can be Solid-state switches, on the other hand, are much faster compared in real time. But using a multiplexer, Figure than relays and can reach sampling rates of several MHz. 3.01, that switches among the inputs of multiple chan- However, these devices can’t handle inputs higher than nels and drives a single ADC can substantially reduce 25V, and they are not well suited for isolated applica- the cost of a system. This approach is used in so-called tions. Moreover, solid-state devices are typically limited sampled-data systems. The higher the sample rate, the to handling currents of only one mA or less. closer the system mimics the ideal data acquisition system. But only a few specialized data acquisition Another characteristic that varies between mechani- systems require sample rates of extraordinary speed. cal relays and solid-state switches is called ON resis- Most applications can cope with the more modest tance. An ideal mechanical switch or relay contact sample rates typically offered by mainstream data pair has zero ON resistance. But real devices such acquisition systems. as common reed-relay contacts are 0.010 W or less, a quality analog switch can be 10 to 100 W, and an Solid State Switches vs.
    [Show full text]