TWO TYPES of PROJECTION Math 225 Suppose That V and W Are
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Linear Algebra for Dummies
Linear Algebra for Dummies Jorge A. Menendez October 6, 2017 Contents 1 Matrices and Vectors1 2 Matrix Multiplication2 3 Matrix Inverse, Pseudo-inverse4 4 Outer products 5 5 Inner Products 5 6 Example: Linear Regression7 7 Eigenstuff 8 8 Example: Covariance Matrices 11 9 Example: PCA 12 10 Useful resources 12 1 Matrices and Vectors An m × n matrix is simply an array of numbers: 2 3 a11 a12 : : : a1n 6 a21 a22 : : : a2n 7 A = 6 7 6 . 7 4 . 5 am1 am2 : : : amn where we define the indexing Aij = aij to designate the component in the ith row and jth column of A. The transpose of a matrix is obtained by flipping the rows with the columns: 2 3 a11 a21 : : : an1 6 a12 a22 : : : an2 7 AT = 6 7 6 . 7 4 . 5 a1m a2m : : : anm T which evidently is now an n × m matrix, with components Aij = Aji = aji. In other words, the transpose is obtained by simply flipping the row and column indeces. One particularly important matrix is called the identity matrix, which is composed of 1’s on the diagonal and 0’s everywhere else: 21 0 ::: 03 60 1 ::: 07 6 7 6. .. .7 4. .5 0 0 ::: 1 1 It is called the identity matrix because the product of any matrix with the identity matrix is identical to itself: AI = A In other words, I is the equivalent of the number 1 for matrices. For our purposes, a vector can simply be thought of as a matrix with one column1: 2 3 a1 6a2 7 a = 6 7 6 . -

Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes
Learning Geometric Algebra by Modeling Motions of the Earth and Shadows of Gnomons to Predict Solar Azimuths and Altitudes April 24, 2018 James Smith [email protected] https://mx.linkedin.com/in/james-smith-1b195047 \Our first step in developing an expression for the orientation of \our" gnomon: Diagramming its location at the instant of the 2016 December solstice." Abstract Because the shortage of worked-out examples at introductory levels is an obstacle to widespread adoption of Geometric Algebra (GA), we use GA to calculate Solar azimuths and altitudes as a function of time via the heliocentric model. We begin by representing the Earth's motions in GA terms. Our representation incorporates an estimate of the time at which the Earth would have reached perihelion in 2017 if not affected by the Moon's gravity. Using the geometry of the December 2016 solstice as a starting 1 point, we then employ GA's capacities for handling rotations to determine the orientation of a gnomon at any given latitude and longitude during the period between the December solstices of 2016 and 2017. Subsequently, we derive equations for two angles: that between the Sun's rays and the gnomon's shaft, and that between the gnomon's shadow and the direction \north" as traced on the ground at the gnomon's location. To validate our equations, we convert those angles to Solar azimuths and altitudes for comparison with simulations made by the program Stellarium. As further validation, we analyze our equations algebraically to predict (for example) the precise timings and locations of sunrises, sunsets, and Solar zeniths on the solstices and equinoxes. -

Schaum's Outline of Linear Algebra (4Th Edition)
SCHAUM’S SCHAUM’S outlines outlines Linear Algebra Fourth Edition Seymour Lipschutz, Ph.D. Temple University Marc Lars Lipson, Ph.D. University of Virginia Schaum’s Outline Series New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto Copyright © 2009, 2001, 1991, 1968 by The McGraw-Hill Companies, Inc. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior writ- ten permission of the publisher. ISBN: 978-0-07-154353-8 MHID: 0-07-154353-8 The material in this eBook also appears in the print version of this title: ISBN: 978-0-07-154352-1, MHID: 0-07-154352-X. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. To contact a representative please e-mail us at [email protected]. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (“McGraw-Hill”) and its licensors reserve all rights in and to the work. -

Equations of Lines and Planes
Equations of Lines and 12.5 Planes Copyright © Cengage Learning. All rights reserved. Lines A line in the xy-plane is determined when a point on the line and the direction of the line (its slope or angle of inclination) are given. The equation of the line can then be written using the point-slope form. Likewise, a line L in three-dimensional space is determined when we know a point P0(x0, y0, z0) on L and the direction of L. In three dimensions the direction of a line is conveniently described by a vector, so we let v be a vector parallel to L. 2 Lines Let P(x, y, z) be an arbitrary point on L and let r0 and r be the position vectors of P0 and P (that is, they have representations and ). If a is the vector with representation as in Figure 1, then the Triangle Law for vector addition gives r = r0 + a. Figure 1 3 Lines But, since a and v are parallel vectors, there is a scalar t such that a = t v. Thus which is a vector equation of L. Each value of the parameter t gives the position vector r of a point on L. In other words, as t varies, the line is traced out by the tip of the vector r. 4 Lines As Figure 2 indicates, positive values of t correspond to points on L that lie on one side of P0, whereas negative values of t correspond to points that lie on the other side of P0. -

Lecture 3.Pdf
ENGR-1100 Introduction to Engineering Analysis Lecture 3 POSITION VECTORS & FORCE VECTORS Today’s Objectives: Students will be able to : a) Represent a position vector in Cartesian coordinate form, from given geometry. In-Class Activities: • Applications / b) Represent a force vector directed along Relevance a line. • Write Position Vectors • Write a Force Vector along a line 1 DOT PRODUCT Today’s Objective: Students will be able to use the vector dot product to: a) determine an angle between In-Class Activities: two vectors, and, •Applications / Relevance b) determine the projection of a vector • Dot product - Definition along a specified line. • Angle Determination • Determining the Projection APPLICATIONS This ship’s mooring line, connected to the bow, can be represented as a Cartesian vector. What are the forces in the mooring line and how do we find their directions? Why would we want to know these things? 2 APPLICATIONS (continued) This awning is held up by three chains. What are the forces in the chains and how do we find their directions? Why would we want to know these things? POSITION VECTOR A position vector is defined as a fixed vector that locates a point in space relative to another point. Consider two points, A and B, in 3-D space. Let their coordinates be (XA, YA, ZA) and (XB, YB, ZB), respectively. 3 POSITION VECTOR The position vector directed from A to B, rAB , is defined as rAB = {( XB –XA ) i + ( YB –YA ) j + ( ZB –ZA ) k }m Please note that B is the ending point and A is the starting point. -

Exercise 7.5
IN SUMMARY Key Idea • A projection of one vector onto another can be either a scalar or a vector. The difference is the vector projection has a direction. A A a a u u O O b NB b N B Scalar projection of a on b Vector projection of a on b Need to Know ! ! ! ! a # b ! • The scalar projection of a on b ϭϭ! 0 a 0 cos u, where u is the angle @ b @ ! ! between a and b. ! ! ! ! ! ! a # b ! a # b ! • The vector projection of a on b ϭ ! b ϭ a ! ! b b @ b @ 2 b # b ! • The direction cosines for OP ϭ 1a, b, c2 are a b cos a ϭ , cos b ϭ , 2 2 2 2 2 2 Va ϩ b ϩ c Va ϩ b ϩ c c cos g ϭ , where a, b, and g are the direction angles 2 2 2 Va ϩ b ϩ c ! between the position vector OP and the positive x-axis, y-axis and z-axis, respectively. Exercise 7.5 PART A ! 1. a. The vector a ϭ 12, 32 is projected onto the x-axis. What is the scalar projection? What is the vector projection? ! b. What are the scalar and vector projections when a is projected onto the y-axis? 2. Explain why it is not possible to obtain! either a scalar! projection or a vector projection when a nonzero vector x is projected on 0. 398 7.5 SCALAR AND VECTOR PROJECTIONS NEL ! ! 3. Consider two nonzero vectors,a and b, that are perpendicular! ! to each other.! Explain why the scalar and vector projections of a on b must! be !0 and 0, respectively. -

MATH 304 Linear Algebra Lecture 24: Scalar Product. Vectors: Geometric Approach
MATH 304 Linear Algebra Lecture 24: Scalar product. Vectors: geometric approach B A B′ A′ A vector is represented by a directed segment. • Directed segment is drawn as an arrow. • Different arrows represent the same vector if • they are of the same length and direction. Vectors: geometric approach v B A v B′ A′ −→AB denotes the vector represented by the arrow with tip at B and tail at A. −→AA is called the zero vector and denoted 0. Vectors: geometric approach v B − A v B′ A′ If v = −→AB then −→BA is called the negative vector of v and denoted v. − Vector addition Given vectors a and b, their sum a + b is defined by the rule −→AB + −→BC = −→AC. That is, choose points A, B, C so that −→AB = a and −→BC = b. Then a + b = −→AC. B b a C a b + B′ b A a C ′ a + b A′ The difference of the two vectors is defined as a b = a + ( b). − − b a b − a Properties of vector addition: a + b = b + a (commutative law) (a + b) + c = a + (b + c) (associative law) a + 0 = 0 + a = a a + ( a) = ( a) + a = 0 − − Let −→AB = a. Then a + 0 = −→AB + −→BB = −→AB = a, a + ( a) = −→AB + −→BA = −→AA = 0. − Let −→AB = a, −→BC = b, and −→CD = c. Then (a + b) + c = (−→AB + −→BC) + −→CD = −→AC + −→CD = −→AD, a + (b + c) = −→AB + (−→BC + −→CD) = −→AB + −→BD = −→AD. Parallelogram rule Let −→AB = a, −→BC = b, −−→AB′ = b, and −−→B′C ′ = a. Then a + b = −→AC, b + a = −−→AC ′. -

Linear Algebra - Part II Projection, Eigendecomposition, SVD
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Punit Shah's slides) 2019 Linear Algebra, Part II 2019 1 / 22 Brief Review from Part 1 Matrix Multiplication is a linear tranformation. Symmetric Matrix: A = AT Orthogonal Matrix: AT A = AAT = I and A−1 = AT L2 Norm: s X 2 jjxjj2 = xi i Linear Algebra, Part II 2019 2 / 22 Angle Between Vectors Dot product of two vectors can be written in terms of their L2 norms and the angle θ between them. T a b = jjajj2jjbjj2 cos(θ) Linear Algebra, Part II 2019 3 / 22 Cosine Similarity Cosine between two vectors is a measure of their similarity: a · b cos(θ) = jjajj jjbjj Orthogonal Vectors: Two vectors a and b are orthogonal to each other if a · b = 0. Linear Algebra, Part II 2019 4 / 22 Vector Projection ^ b Given two vectors a and b, let b = jjbjj be the unit vector in the direction of b. ^ Then a1 = a1 · b is the orthogonal projection of a onto a straight line parallel to b, where b a = jjajj cos(θ) = a · b^ = a · 1 jjbjj Image taken from wikipedia. Linear Algebra, Part II 2019 5 / 22 Diagonal Matrix Diagonal matrix has mostly zeros with non-zero entries only in the diagonal, e.g. identity matrix. A square diagonal matrix with diagonal elements given by entries of vector v is denoted: diag(v) Multiplying vector x by a diagonal matrix is efficient: diag(v)x = v x is the entrywise product. Inverting a square diagonal matrix is efficient: 1 1 diag(v)−1 = diag [ ;:::; ]T v1 vn Linear Algebra, Part II 2019 6 / 22 Determinant Determinant of a square matrix is a mapping to a scalar. -

Basics of Linear Algebra
Basics of Linear Algebra Jos and Sophia Vectors ● Linear Algebra Definition: A list of numbers with a magnitude and a direction. ○ Magnitude: a = [4,3] |a| =sqrt(4^2+3^2)= 5 ○ Direction: angle vector points ● Computer Science Definition: A list of numbers. ○ Example: Heights = [60, 68, 72, 67] Dot Product of Vectors Formula: a · b = |a| × |b| × cos(θ) ● Definition: Multiplication of two vectors which results in a scalar value ● In the diagram: ○ |a| is the magnitude (length) of vector a ○ |b| is the magnitude of vector b ○ Θ is the angle between a and b Matrix ● Definition: ● Matrix elements: ● a)Matrix is an arrangement of numbers into rows and columns. ● b) A matrix is an m × n array of scalars from a given field F. The individual values in the matrix are called entries. ● Matrix dimensions: the number of rows and columns of the matrix, in that order. Multiplication of Matrices ● The multiplication of two matrices ● Result matrix dimensions ○ Notation: (Row, Column) ○ Columns of the 1st matrix must equal the rows of the 2nd matrix ○ Result matrix is equal to the number of (1, 2, 3) • (7, 9, 11) = 1×7 +2×9 + 3×11 rows in 1st matrix and the number of = 58 columns in the 2nd matrix ○ Ex. 3 x 4 ॱ 5 x 3 ■ Dot product does not work ○ Ex. 5 x 3 ॱ 3 x 4 ■ Dot product does work ■ Result: 5 x 4 Dot Product Application ● Application: Ray tracing program ○ Quickly create an image with lower quality ○ “Refinement rendering pass” occurs ■ Removes the jagged edges ○ Dot product used to calculate ■ Intersection between a ray and a sphere ■ Measure the length to the intersection points ● Application: Forward Propagation ○ Input matrix * weighted matrix = prediction matrix http://immersivemath.com/ila/ch03_dotprodu ct/ch03.html#fig_dp_ray_tracer Projections One important use of dot products is in projections. -

An Elementary System of Axioms for Euclidean Geometry Based on Symmetry Principles
An Elementary System of Axioms for Euclidean Geometry based on Symmetry Principles Boris Čulina Department of Mathematics, University of Applied Sciences Velika Gorica, Zagrebačka cesta 5, Velika Gorica, CROATIA email: [email protected] arXiv:2105.14072v1 [math.HO] 28 May 2021 1 Abstract. In this article I develop an elementary system of axioms for Euclidean geometry. On one hand, the system is based on the symmetry principles which express our a priori ignorant approach to space: all places are the same to us (the homogeneity of space), all directions are the same to us (the isotropy of space) and all units of length we use to create geometric figures are the same to us (the scale invariance of space). On the other hand, through the process of algebraic simplification, this system of axioms directly provides the Weyl’s system of axioms for Euclidean geometry. The system of axioms, together with its a priori interpretation, offers new views to philosophy and pedagogy of mathematics: (i) it supports the thesis that Euclidean geometry is a priori, (ii) it supports the thesis that in modern mathematics the Weyl’s system of axioms is dominant to the Euclid’s system because it reflects the a priori underlying symmetries, (iii) it gives a new and promising approach to learn geometry which, through the Weyl’s system of axioms, leads from the essential geometric symmetry principles of the mathematical nature directly to modern mathematics. keywords: symmetry, Euclidean geometry, axioms, Weyl’s axioms, phi- losophy of geometry, pedagogy of geometry 1 Introduction The connection of Euclidean geometry with symmetries has a long history. -
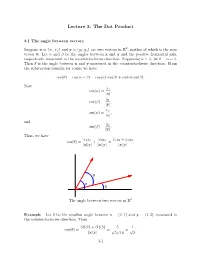
The Dot Product
Lecture 3: The Dot Product 3.1 The angle between vectors 2 Suppose x = (x1; x2) and y = (y1; y2) are two vectors in R , neither of which is the zero vector 0. Let α and β be the angles between x and y and the positive horizontal axis, respectively, measured in the counterclockwise direction. Supposing α β, let θ = α β. Then θ is the angle between x and y measured in the counterclockwise≥ direction. From− the subtraction formula for cosine we have cos(θ) = cos(α β) = cos(α) cos(β) + sin(α) sin(β): − Now x cos(α) = 1 ; x j j y cos(β) = 1 ; y j j x sin(α) = 2 ; x j j and y sin(β) = 2 : y j j Thus, we have x y x y x y + x y cos(θ) = 1 1 + 2 2 = 1 1 2 2 : x y x y x y j jj j j jj j j jj j θ α β The angle between two vectors in R2 Example Let θ be the smallest angle between x = (2; 1) and y = (1; 3), measured in the counterclockwise direction. Then (2)(1) + (1)(3) 5 1 cos(θ) = = = : x y p5p10 p2 j jj j 3-1 Lecture 3: The Dot Product 3-2 Hence 1 1 π θ = cos− = : p2 4 With more work it is possible to show that if x = (x1; x2; x3) and y = (y1; y2; y3) are two vectors in R3, neither of which is the zero vector 0, and θ is the smallest positive angle between x and y, then x y + x y + x y cos(θ) = 1 1 2 2 3 3 x y j jj j 3.2 The dot product n Definition If x = (x1; x2; : : : ; xn) and y = (y1; y2; : : : ; yn) are vectors in R , then the dot product of x and y, denoted x y, is given by · x y = x1y1 + x2y2 + + xnyn: · ··· Note that the dot product of two vectors is a scalar, not another vector. -

Quantum Flatland and Monolayer Graphene from a Viewpoint of Geometric Algebra A
Vol. 124 (2013) ACTA PHYSICA POLONICA A No. 4 Quantum Flatland and Monolayer Graphene from a Viewpoint of Geometric Algebra A. Dargys∗ Center for Physical Sciences and Technology, Semiconductor Physics Institute A. Go²tauto 11, LT-01108 Vilnius, Lithuania (Received May 11, 2013) Quantum mechanical properties of the graphene are, as a rule, treated within the Hilbert space formalism. However a dierent approach is possible using the geometric algebra, where quantum mechanics is done in a real space rather than in the abstract Hilbert space. In this article the geometric algebra is applied to a simple quantum system, a single valley of monolayer graphene, to show the advantages and drawbacks of geometric algebra over the Hilbert space approach. In particular, 3D and 2D Euclidean space algebras Cl3;0 and Cl2;0 are applied to analyze relativistic properties of the graphene. It is shown that only three-dimensional Cl3;0 rather than two-dimensional Cl2;0 algebra is compatible with a relativistic atland. DOI: 10.12693/APhysPolA.124.732 PACS: 73.43.Cd, 81.05.U−, 03.65.Pm 1. Introduction mension has been reduced, one is automatically forced to change the type of Cliord algebra and its irreducible Graphene is a two-dimensional crystal made up of car- representation. bon atoms. The intense interest in graphene is stimulated On the other hand, if the problem was formulated in by its potential application in the construction of novel the Hilbert space terms then, generally, the neglect of nanodevices based on relativistic physics, or at least with one of space dimensions does not spoil the Hilbert space.