DOCSLIB.ORG

Applying Path Planning Algorithms to Train Schedules

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Applying Path Planning Algorithms to Train Schedules Applying Path Planning Algorithms to Train Schedules Tim Soethout 3117901 Universiteit Utrecht February 1, 2012 < Shl, −2, a, 12 : 44 > < Shl, −2, d, 12 : 43 > 0 0 < Shl, −2, d, 12 : 44 > < Shl, −2, d, 12 : 42 >0 8 <0 Shl, 3545, d, 12 : 44 > 8 < Shl, −2, a, 12 : 34 > < Asdz, 3545, a, 12 : 52 > 1 < Shl, −2, a, 12 : 33 > 1 < Asdz, 3545, d, 12 : 53 > 0 5 < Shl, −2, a, 12 : 32 > < Asb, 3545, a, 12 : 58 > 5 1 < Shl, 2649, a, 12 : 27 > < Asb, 3545, d, 12 : 59 > 6 < Asdl, 2649, d, 12 : 21 > 17 < Ut, 3545, a, 13 : 16 > 0 < Asdl, 2649, a, 12 : 21 > 1 0 < Ass, −2, a, 12 : 36 > 1 4 0 1 < Ass, −2, a, 12 : 37 > < Ass, −2, d, 12 : 35 > 0 3 3 0 < Ut, −4, a, 14 : 00 > 5 < Ass, 2649, d, 12 : 17 > < Ass, −2, a, 12 : 323 > 5 5 < Ass, −2, d, 12 : 43 > 0 1 1 1 000 0 0 0 0 0 0 0 0 < Ass, 3045, d, 12 : 43 > 1 < Ass, −2, d, 12 : 31 > < Ass, 2649, a, 12 : 16 > 5 1 < Ut, 3045, a, 13 : 19 > 6 6 6 1 1 19 < Ass, −2, a, 12 : 20 > 51 < Ass, − , a, > < Asd, 3045, a, 12 : 49 > 5 1 2 12 : 21 < Ass, −2, a, 12 : 29 > 19 19 19 5 3 33 19 < Ass, 2249, a, 12 : 15 > 5 5 5 3 1 19 19 3 3 19 19 < Ass, −2, a, 12 : 24 > 3 1 1 1 1 1 7 5 5 < Asd, 2649, d, 12 : 11 > 1 1 < Ass, −2, d, 12 : 25 > 2 < Asa, 3045, d, 13 : 00 > 1 1 1 7 < Asd, 3045, d, 12 : 52 > < Asd, 2249, d, 12 : 10 > 1 2 22 1 0 5 7 77 0 5 2 < Ass, −2, d, 12 : 28 > 1 < Asa, 3045, a, 12 : 59 > < Ass, 3034, a, 12 : 19 > 7 2 0 0 1 0 1 0 0 0 00 00 1 < Asd, −2, d, 12 : 10 > 11 1 1 1 7 0 0 11 1 < Asd, − , d, > 0 2 12 : 11 < Asa, −2, d, 13 : 00 > < Asd, −2, d, 12 : 52 > 1 0 1 1 < Ass, 845, d, 12 : 28 > 1 0 < Asd, −2, a, 12 : 09 > 11 6 0 1 1 1 7 6 0 < Asd, −2, a, 12 : 08 > 0 1 1 11 1 66 < Asd, −2, d, 12 : 07 > 1 1 0 < Asd,1 3034, d, 12 : 12 > 6 11 11 6 00 00 6 6 6 6 6 0 0 1 < Asd, 845, a, 12 : 34 > < Asd, −2, a, 12 : 06 > 0 0 1 5 5 11 5 0 < Asa, −2, a, 12 : 49 > 6 0 < Asd, −2, d, 120 : 12 >0 < Asd, −3, d, 12 : 00 > 0 6 < Asa, −2, a, 12 : 49 > < Asd, −2, a, 12 : 46 > 2 < Asd, −2, a, 12 : 39 > 1 6 2 1 1 2 < Asa, −2, d, 12 : 45 > 3 1 < Asd, −2, d, 12 : 40 > 0 0 00 1 1 0 1 1 5 < Asd, −2, a, 12 : 14 > 0 8 < Asd, −2, d, 12 : 41 > < Asd, −2, d, 12 : 45 > < Asa, −2, d, 12 : 45 > 1 0 2 0 0 0 8 8 < Asa, 845, a, 12 : 44 > 8 1 2 < Asd, −2, a, 12 : 44 > 1 1 < Asd, −2, d, 12 : 22 > 0 2 < Asa, −2, a, 12 : 36 > < Asd, −2, d, 12 : 42 > < Asd, −2, a, 12 : 38 > 2 < Asd, 3043, d, 12 : 22 > 7 7 2 5 < Asa, −2, a, 12 : 341> < Asd, 845, d, 12 : 37 > 2 < Asa, 3043, a, 12 : 29 > 1 < Asd, −2, d, 12 : 370> < Asd, −2, a, 12 : 24 > 0 0 0 0 < Asd, −2, a, 12 : 36 > < Asd, −2, d, 12 : 25 > 0 2 2 0 < Asd, −2, d, 12 : 34 > < Asd, −2, a, 12 : 25 > 4 1 4 1 < Asd, −2, d, 12 : 29 > < Asd, −2, a, 12 : 27 > 0 0 0 < Asd, −2, a, 12 :1 27 > 1 < Asd, −2, d, 12 : 27 > 0 Bachelor’s thesis Cognitive Artificial Intelligence (15 ECTS) Supervisor: dhr. prof. dr. Vincent van Oostrom Contents 1 Introduction 3 2 Representation 3 2.1 Formal...............................................3 2.1.1 Basic vertices and edges.................................3 2.1.2 Costs...........................................4 2.1.3 Station Lines.......................................5 2.1.4 Departure and Arrival vertices.............................6 2.1.5 Possible extensions....................................7 2.2 Correct/usable?.........................................7 2.2.1 Pruning..........................................7 3 Shortest Path Problem7 3.1 Introduction............................................7 3.2 Algorithms............................................7 3.2.1 Dijkstra’s Algorithm...................................7 3.2.2 Bellman-Ford.......................................8 3.2.3 k Shortest Paths.....................................9 4 Implementation 12 4.1 General.............................................. 12 4.2 Representation.......................................... 14 4.2.1 Data Set.......................................... 14 4.2.2 Implementation...................................... 15 4.2.3 Time Complexity..................................... 17 4.2.4 Performance....................................... 17 4.3 Algorithms............................................ 17 4.3.1 Dijkstra’s Algorithm................................... 17 4.3.2 Bellman-Ford....................................... 19 4.3.3 k Shortest Paths..................................... 19 4.4 Visualisation........................................... 20 4.5 Performance............................................ 20 5 Conclusion 22 6 Future Work 23 6.1 Graph Representation...................................... 23 6.2 Algorithm............................................. 23 A Source files 25 A.1 Station Abbreviations source file................................ 25 A.2 Made up time table source file................................. 28 2 1 Introduction This bachelor’s thesis for Cognitive Artificial Intelligence began with an idea to do something with trains. Of course it had something to do with one or more of the foundations of the study of cognitive artificial intelligence. It soon became clear the emphasis would be on logic and computer science. This rather broad subject had soon to become more defined than this vague notion of combining trains, logic and computers. There are many possibilities spreading from an artificial intelligence for building the perfect train transportation systems in game like environments like the classic computer game Transport Tycoon to giving the best travel advice to a person to get from A to B or generating a train time schedule from scratch. As every enthusiastic student I set out to do as much as possible, but quickly limited my view to the shortest path problem. This is the problem of getting from A to B in the cheapest way. It soon became clear that to tackle this problem much more comes to the surface than simply running a shortest path algorithm such as the well known Dijkstra’s algorithm. The first step is to figure out a way to represent the train time table into a graph model on which the algorithms can be run. It all began with a very simple representation and all seemed trivial at first, but a lot more had to be done to really grasp all the features of the train time table. Also extensibility and generality had to be kept in mind. The second step was to study some algorithms to generate the correct travel advise. This could be done with shortest path algorithms. The obvious Dijkstra’s algorithm is of course described. But more interesting was the k shortest path algorithm. Especially for its relevance for this application to give alternative travel advise. The main focus lies on Eppstein’s version of the k shortest path algorithm. This thesis is divided in three main parts. The first part is the logic, theoretic part of the representation of the time table graph and can be found in section2. The second part is a study into the shortest path problem and the different shortest path algorithm and is found in section3. The third and biggest part is the implementation of the representation and the shortest path algorithms and found in section4. The accompanying source code of the implementation is attached. Before I start off with the content I would like to thank the following people for their support: Vincent van Oostrom for supervising me for this extended period of time, Jochem Bongaerts for constantly being available for discussions to re-order my mind on the subject and many more people for constantly reminding me to finish my bachelors thesis already. It is here at last. 2 Representation 2.1 Formal 2.1.1 Basic vertices and edges We represent a time table of a train as a graph over which the algorithms can generate their response. We start by defining a directed graph G containing vertices (V ) and edges (E). G = hV, Ei1 Each vertex is a set with the following properties: V = hS, R, K, T i + Where S is a station, R ∈ R ∪ {aa, ad, st} where the numbers denote a route number or the arrival (aa) or departure (ad) vertex for an algorithm or station line (st), K ∈ {d, a} indicates a departure or an arrival and T is the corresponding time. S is denoted with an abbreviation for a specific station, mapping can be found in the Appendix on page 25. A vertex can be seen on figure1. Transitions (edges) are of form: E = hV, W, V i The first V is the source vertex and the second V the target vertex. W ∈ {t, w} describes whether the transit is a real transfer or a wait in a train, this is important for the number of hops. In most cases W will be w, only when a transfer from station line into a train is done t will be used. This will become clear in section 2.1.3. An edge can be seen on figure2. Note that the ∆T is also displayed in the pictures 1The structure of the graph is inspired on the graphs used to create the dutch railways timetables[Sch08]. 3 Asd, 1, d, 13.30 Asd, 1, d, 13.30 Asd, 1, a, 13.30 Figure 1: Vertex represent- t, 20m w, 10m ing Amsterdam central station, route number 1 and departure at 13.30h.
Load more

Recommended publications
  • Indeling Van Nederland in 40 COROP-Gebieden Gemeentelijke Indeling Van Nederland Op 1 Januari 2019
    Indeling van Nederland in 40 COROP-gebieden Gemeentelijke indeling van Nederland op 1 januari 2019 Legenda COROP-grens Het Hogeland Schiermonnikoog Gemeentegrens Ameland Woonkern Terschelling Het Hogeland 02 Noardeast-Fryslân Loppersum Appingedam Delfzijl Dantumadiel 03 Achtkarspelen Vlieland Waadhoeke 04 Westerkwartier GRONINGEN Midden-Groningen Oldambt Tytsjerksteradiel Harlingen LEEUWARDEN Smallingerland Veendam Westerwolde Noordenveld Tynaarlo Pekela Texel Opsterland Súdwest-Fryslân 01 06 Assen Aa en Hunze Stadskanaal Ooststellingwerf 05 07 Heerenveen Den Helder Borger-Odoorn De Fryske Marren Weststellingwerf Midden-Drenthe Hollands Westerveld Kroon Schagen 08 18 Steenwijkerland EMMEN 09 Coevorden Hoogeveen Medemblik Enkhuizen Opmeer Noordoostpolder Langedijk Stede Broec Meppel Heerhugowaard Bergen Drechterland Urk De Wolden Hoorn Koggenland 19 Staphorst Heiloo ALKMAAR Zwartewaterland Hardenberg Castricum Beemster Kampen 10 Edam- Volendam Uitgeest 40 ZWOLLE Ommen Heemskerk Dalfsen Wormerland Purmerend Dronten Beverwijk Lelystad 22 Hattem ZAANSTAD Twenterand 20 Oostzaan Waterland Oldebroek Velsen Landsmeer Tubbergen Bloemendaal Elburg Heerde Dinkelland Raalte 21 HAARLEM AMSTERDAM Zandvoort ALMERE Hellendoorn Almelo Heemstede Zeewolde Wierden 23 Diemen Harderwijk Nunspeet Olst- Wijhe 11 Losser Epe Borne HAARLEMMERMEER Gooise Oldenzaal Weesp Hillegom Meren Rijssen-Holten Ouder- Amstel Huizen Ermelo Amstelveen Blaricum Noordwijk Deventer 12 Hengelo Lisse Aalsmeer 24 Eemnes Laren Putten 25 Uithoorn Wijdemeren Bunschoten Hof van Voorst Teylingen
    [Show full text]
  • Historisch Onderzoek Nen5725 Gelriaweg 16 Te Epe
    HISTORISCH ONDERZOEK NEN5725 GELRIAWEG 16 TE EPE VMI GROUP EPE 21 juli 2014 077998780:A B03203.000018.0100 Historisch onderzoek NEN5725 Gelriaweg 16 te Epe Inhoud 1 Inleiding, doel en probleemstelling ................................................................................................................. 3 2 Bodemgebruik ...................................................................................................................................................... 5 2.1 Voormalige bodemgebruik ....................................................................................................................... 5 2.2 Huidige bodemgebruik ............................................................................................................................. 5 2.3 Toekomstig bodemgebruik....................................................................................................................... 5 3 Bestaande bodeminformatie .............................................................................................................................. 6 3.1 Bodemopbouw en geologie ...................................................................................................................... 6 3.2 bodemkwaliteitskaart ................................................................................................................................ 6 3.3 Asbestkaart ................................................................................................................................................
    [Show full text]
  • Netherlands Web 2006
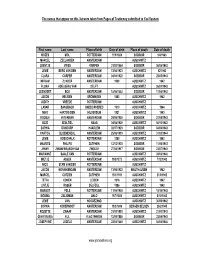
    The names that appear on this list were taken from Pages of Testimony submitted to Yad Vashem First name Last name Place of birth Date of birth Place of death Date of death MOZES MOL ROTTERDAM 17/9/1889 SOBIBOR 9/4/1943 MARCEL ZEELANDER AMSTERDAM AUSCHWITZ LEENTJE VRIES KAMPEN 21/03/1884 SOBIBOR 08/06/1943 LEVIE BERG VAN DEN AMSTERDAM 13/04/1923 AUSCHWITZ 02/1942 CLARA CORPER AMSTERDAM 04/04/1922 SOBIBOR 28/05/1943 MIRJAM ZLINDER AMSTERDAM 1909 AUSCHWITZ 1942 FLORA ADELBERG VAN DELFT AUSCHWITZ 26/01/1943 LEENDERT BOS AMSTERDAM 18/06/1883 SOBIBOR 11/06/1943 JACOB HEIJDEN GRONINGEN 1883 AUSCHWITZ 1942 JUDITH VREEDE ROTTERDAM AUSCHWITZ LASAR BANGBACH UNDECIPHERED 1910 AUSCHWITZ 1944 NIKO HARTOG DEN HILVERSUM 1921 AUSCHWITZ 1943 ROOSJE VETERMAN AMSTERDAM 29/09/1900 SOBIBOR 21/05/1943 SUZE SEALTIEL HAAG 04/08/1929 AUSCHWITZ 08/10/1942 SOPHIA DONDORP HAARLEM 02/07/1929 SOBIBOR 04/06/1943 HARTOG BLOEMENDAL AMSTERDAM 25/06/1919 AUSCHWITZ 31/03/1944 LEVIE GOSSCHALK ROTTERDAM 1889 AUSCHWITZ 1942 MAURITS PHILIPS ZUTPHEN 12/12/1935 SOBIBOR 11/06/1943 JENNY ZWANENBURGH VAN ZWOLLE 27/08/1917 SOBIBOR 23/07/1943 MARIANNE BAALE VAN ROTTERDAM AUSCHWITZ 03/08/1942 MIETJE ASSER AMSTERDAM 19/3/1873 AUSCHWITZ 7/12/1942 NICO STAM VAN DER ROTTERDAM AUSCHWITZ JACOB MONNIKENDAM AMSTERDAM 13/06/1922 MAUTHAUSEN 1942 MARCEL CUTZIEN ZUTPHEN 15/1/1931 AUSCHWITZ 21/9/1942 TETTA COHEN LEIDEN 1916 AUSCHWITZ 1942 LINTJE VISSER DELFZIJL 1886 AUSCHWITZ 1942 MARGOT PELS ROTTERDAM 11/09/1905 AUSCHWITZ 15/10/1942 MOSINA ZALIGMAN ANLO 15/7/1886 AUSCHWITZ 8/10/1942 LEVIE VAN
    [Show full text]
  • Tweede Kamer Der Staten-Generaal 2
    Tweede Kamer der Staten-Generaal 2 Vergaderjaar 2003–2004 28 855 Gemeentelijke herindeling van een deel van de Achterhoek, de Graafschap en de Liemers en Bathmen, tevens wijziging van de grens tussen de provincies Gelderland en Overijssel Nr. 18 AMENDEMENT VAN DE LEDEN VAN DER HAM EN EERDMANS Ontvangen 30 januari 2004 De ondergetekenden stellen het volgende amendement voor: I In artikel 1 vervallen «Borculo», «Eibergen», «Neede» en «Ruurlo». II In artikel 2, eerste lid, vervalt «Berkelland». III In de tabel van artikel 2, tweede lid, vervalt: Berkelland Borculo Eibergen Neede Ruurlo IV In artikel 4 wordt «Rijnwaarden en Doetinchem» vervangen door: Eibergen, Ruurlo, Rijnwaarden en Doetinchem. V In de tabel van artikel 5 vervalt: Berkelland Eibergen KST74016 0304tkkst28855-18 ISSN 0921 - 7371 Sdu Uitgevers ’s-Gravenhage 2004 Tweede Kamer, vergaderjaar 2003–2004, 28 855, nr. 18 1 VI In de tabel van artikel 6 vervalt: Berkelland Borculo Eibergen Neede Ruurlo VII Artikel 8, onderdeel b, komt als volgt te luiden: b. Het gestelde onder «Arrondissement Zutphen» wordt vervangen door: Aalten, Apeldoorn, Borculo, Bronckhorst, Brummen, Doetinchem, Eibergen, Elburg, Epe, Ermelo, Groenlo, Harderwijk, Hattem, Heerde,Lo- chem, Montferland, Neede, Nunspeet, Oldebroek, Putten, Ruurlo, Oude IJsselstreek, Voorst, Winterswijk, Zutphen. VIII Artikel 10, onderdeel b., komt als volgt te luiden: b. Het gestelde onder «Noord- en Oost-Gelderland» wordt vervangen door: Apeldoorn, Aalten, Borculo, Bronckhorst, Brummen, Doetinchem, Eibergen, Elburg, Epe, Ermelo, Groenlo, Harderwijk, Hattem, Heerde, Lochem, Montferland, Neede, Nunspeet, Oldebroek, Oude IJsselstreek, Putten, Ruurlo, Voorst, Winterswijk, Zutphen. IX De kaart, behorende bij de wet wordt gewijzigd zoals aangegeven op het bij dit amendement behorende kaartbeeld1.
    [Show full text]
  • Estimating Railway Ridership
    28-04-2016 Estimating Railway Ridership DEMAND FOR NEW RAILWAY STATIONS IN THE NETHERLANDS TSJIBBE HARTHOLT S1496352 COMMITTEE: K. GEURS (Chairman) University of Twente L. LA PAIX PUELLO University of Twente T. BRANDS Goudappel Coffeng 0 1 I. SUMMARY Demand estimation for new railway stations is an essential step in determining the feasibility of a new proposed railway stations. Multiple demand estimation models already exist. However these are not always accurate or freely available for use. Therefore a new demand estimation model was developed which is able to provide rail ridership estimations. Main question of this thesis that will be answered is: How can the daily number of passengers of a new train station be forecasted on the basis of departure station choice and network accessibility? Aim is to estimate a demand estimation model which is valid for the whole of the Netherlands and focusses on proposed sprinter train stations. Factors determining total rail ridership Rail ridership can be determined by three main factors: Built environment factors Socio-economic factors Network dependent factors Built environment factors are factors that describe the situation in the direct environment of the station. A subdivision can be made into station environment factors based on the three d’s as described by Cervero and Knockel-man (1997): o Density: Describing the amount of activities in the proximity of the station. This could be the e.g. number of jobs, number of students, shops or total population. o Diversity: describing the diversity of the activities that take place in the proximity of the station. o Design: variables describing the properties of a station (area) as a direct consequence of its design.
    [Show full text]
  • 2009-04-06 Toegankelijkheid Gemeentes Volledig
    ID_BUSH_PL GEMEENTE KERN HALTENAAM 1.152 Barneveld Barneveld Station Centrum 11.013 Bronckhorst Vorden Horsterkamp Zuid 8.095 Bronckhorst Vorden Station 10.669 Bronckhorst Vorden Station 1.911 Bronckhorst Zelhem Markt 10.552 Bronckhorst Zelhem Markt 815 Brummen Eerbeek Loubergweg 6.063 Brummen Eerbeek Loubergweg 812 Brummen Eerbeek Ringlaan 6.056 Brummen Eerbeek Ringlaan 813 Brummen Eerbeek Vondellaan 6.057 Brummen Eerbeek Vondellaan 8.452 Doetinchem Doetinchem Slingeland Ziekenhuis 8.577 Druten buitengebied Koningstraat 9.695 Druten buitengebied Scharrenburg/N322 9.694 Druten buitengebied Scharrenburg/N322 15.238 Druten Deest Grotestraat 13.312 Druten Druten Busstation 9.702 Druten Druten Busstation 13.587 Druten Druten Busstation 9.688 Druten Druten Hermes Garage 9.685 Druten Druten Markt 9.686 Druten Druten Markt 9.683 Druten Druten Pax Christi College 9.689 Druten Druten Pax Christi College 6.185 Ede Ede Bovenbuurtweg 6.184 Ede Ede Bovenbuurtweg 13.569 Ede Ede Ede / Wageningen Zd 9.988 Ede Ede Stadspoort 6.326 Ede Ede Stadspoort 10.633 Ede Ede Zkh Gelderse Vallei 10.634 Ede Ede Zkh Gelderse Vallei 2.325 Elburg Elburg Centrum 2.328 Elburg Elburg Coragestraat 2.334 Elburg Elburg Het Nieuwe Feithenhof 8.469 Elburg Elburg Het Nieuwe Feithenhof 2.324 Elburg Elburg Molendorp 8.467 Elburg Elburg Zwolscheweg 2.329 Elburg Oostendorp Klokbekerweg 8.464 Elburg Oostendorp Klokbekerweg 2.530 Ermelo Ermelo Hamburgerweg 6.457 Ermelo Ermelo Hamburgerweg 2.486 Lochem Harfsen School 2.487 Lochem Harfsen School 3.508 Neder-Betuwe Kesteren Station 2.622 Nijkerk Nijkerk Station NS 6.442 Nijkerk Nijkerk Station NS 2.611 Nijkerk Nijkerk Tinbergenlaan 6.438 Nijkerk Nijkerk Tinbergenlaan 2.613 Nijkerk Nijkerk Van Renselaerstraat 6.439 Nijkerk Nijkerk Van Renselaerstraat 6.453 Nijkerk Nijkerk Zilverschoon 2.615 Nijkerk Nijkerk Zilverschoon 6.436 Nijkerk Nijkerkerveen Centrum 2.605 Nijkerk Nijkerkerveen Centrum 1.217 Nunspeet Elspeet Centrum 10.333 Nunspeet Nunspeet Boterdijk 2.267 Oldebroek Wezep W.
    [Show full text]
  • The Roots of Nationalism
    HERITAGE AND MEMORY STUDIES 1 HERITAGE AND MEMORY STUDIES Did nations and nation states exist in the early modern period? In the Jensen (ed.) field of nationalism studies, this question has created a rift between the so-called ‘modernists’, who regard the nation as a quintessentially modern political phenomenon, and the ‘traditionalists’, who believe that nations already began to take shape before the advent of modernity. While the modernist paradigm has been dominant, it has been challenged in recent years by a growing number of case studies that situate the origins of nationalism and nationhood in earlier times. Furthermore, scholars from various disciplines, including anthropology, political history and literary studies, have tried to move beyond this historiographical dichotomy by introducing new approaches. The Roots of Nationalism: National Identity Formation in Early Modern Europe, 1600-1815 challenges current international scholarly views on the formation of national identities, by offering a wide range of contributions which deal with early modern national identity formation from various European perspectives – especially in its cultural manifestations. The Roots of Nationalism Lotte Jensen is Associate Professor of Dutch Literary History at Radboud University, Nijmegen. She has published widely on Dutch historical literature, cultural history and national identity. Edited by Lotte Jensen The Roots of Nationalism National Identity Formation in Early Modern Europe, 1600-1815 ISBN: 978-94-6298-107-2 AUP.nl 9 7 8 9 4 6 2 9 8 1 0 7 2 The Roots of Nationalism Heritage and Memory Studies This ground-breaking series examines the dynamics of heritage and memory from a transnational, interdisciplinary and integrated approaches.
    [Show full text]
  • NOTA Ruimtelijke Kwaliteit BRUMMEN VOORWOORD
    NOTA Ruimtelijke Kwaliteit BRUMMEN VOORWOORD De gemeente Brummen heeft veel moois te bieden. Van historische landschappen tot statige herenhuizen, van schitterend natuurschoon tot gezellige dorpen en buurtschappen. De gemeente Brummen is een gemeente met veel gezichten in een aantrekkelijke en goed verzorgde omgeving. Dit verhoogt de kwaliteit van Voorwoord de dagelijkse leef-, woon- en werkomgeving en de waarde van het onroerend goed. Maar hoe houden we dat met elkaar zo? De één wil zijn erfafscheiding uitbreiden of een dakkapel plaatsen, de ander wil een reclamebord aan zijn gevel of een zonnepaneel op het dak. Allemaal prachtige initiatieven, maar hoe gaan we daarmee om en zorgen we dat Brummen zijn schoonheid behoudt? Het welstandsbeleid van de gemeente Brummen is daar een belangrijk instrument voor. Het zorgt voor de kwaliteit van de gebouwde omgeving. Om het welstandsbeleid voor burgers inzichtelijk te maken, is er een Nota Ruimtelijke Kwaliteit, voorheen welstandsnota, opgesteld. Deze nota is in samenwerking met het Gelders Genootschap tot stand gekomen. De Nota Ruimtelijke Kwaliteit die voor u ligt, is een inspiratiebron voor kwaliteit en duurzaamheid. Het bevat handvatten voor verbouwingen en beschrijft hoe om te gaan met verbouwingen aan huizen, bedrijven, landgoederen en monumenten. Ook worden suggesties gegeven over duurzaamheid en worden oplossingsrichtingen gegeven voor de herindeling van boerenerven. Via deze nota kunt u zich vooraf verdiepen zodat u weet welke eisen aan uw verbouwings- of uitbreidingsaanvraag worden gesteld. Samen houden we de kwaliteit van de gemeente Brummen op peil! Wij wensen u een plezierige tijd in de gemeente Brummen. Vriendelijke groet, Hennie Beelen Wethouder Ruimtelijke Ordening en Duurzaamheid INHOUDSOPGAVE 01.
    [Show full text]
  • De Bevolking Van De Regio Gelre-Ijssel, 2006
    1 De bevolking van de regio Gelre-IJssel De gezondheid van de bevolking hangt samen met demografische en sociaal- economische factoren. Zo leven lager opgeleide mannen en vrouwen gemiddeld korter dan hoog opgeleiden. Het gemiddelde verschil in het aantal jaren dat in minder goede gezondheid wordt doorgebracht is zo’n 15 jaar. Deze verschillen nemen niet af in de tijd. Demografische en sociaal-economische factoren zijn ook sterk gerelateerd aan stedelijkheid waardoor er in de steden andere gezondheidsproblemen te verwachten zijn dan in de dorpen en het buiten- gebied. Zo vinden we in alle grote Nederlandse steden sociaal-economische gezondheidsverschillen tussen wijken. Veel studies hebben aangetoond dat slechte gezondheid en schadelijk gezondheidsgedrag vaker voorkomen in achterstandswijken. Een beschrijving van de kerncijfers voor de gemeenten in de regio Gelre-IJssel geeft inzicht in de gezondheidsproblemen die kunnen optreden. DE REGIO GELRE-IJSSEL Gemeente Aantal Bevolkingsdichtheid Sinds 1 januari 2005 bestaat de regio Gelre-IJssel uit de inwoners (inw/km2) volgende 15 gemeenten: Aalten, Apeldoorn, Berkelland, Bronckhorst, Brummen, Deventer, Doetinchem, Epe, Aalten 27.446 284 Lochem, Montferland, Oost Gelre (voorheen Groenlo en Apeldoorn 156.064 459 Lichtenvoorde), Oude-IJsselstreek, Voorst, Winterswijk en Berkelland 45.227 175 Bronckhorst 37.616 133 Zutphen. Bijna alle gemeenten liggen in de provincie Brummen 21.403 255 Gelderland, alleen Deventer behoort bij de provincie Deventer 95.620 703 Overijssel. Een aantal van deze gemeenten is ontstaan na Doetinchem 56.754 717 gemeentelijke herindelingen die hebben plaatsgevonden. Epe 33.108 212 De regio Gelre-IJssel is een uitgestrekte regio die circa Groenlo 30.416 277 2322 km2 beslaat.
    [Show full text]
  • 0182038 Folder Hoogwater Brummen.Indd
    Hoogwater in Cortenoever Wat te doen voor, tijdens en na hoogwater en evacuatie Voorwoord Leven met het water, verantwoordelijkheid van gemeente én inwoners U woont in een mooi gebied aan de IJssel. Door de eeuwen heen hebben mensen hier leren leven met het water. Steeds hogere en bredere dijken hebben de kans op een overstroming sterk doen afnemen. Maar nog altijd moeten we leven met het water. Dat bleek wel in 1995, toen het water tot grote hoogte steeg. Dit maakte duidelijk dat de rivier meer ruimte nodig had om ook in de toekomst het water veilig af te voeren. In de afgelopen jaren zijn hiervoor overal langs de grote rivieren maatregelen genomen. Zoals de dijkverlegging in Cortenoever, die sinds 2017 klaar is. In deze folder leest u meer over hoogwater na deze dijkverlegging. Zolang het water niet extreem hoog stijgt, houden de kades (de oude dijken) het water tegen. Zo blijft het gebied achter de kades en tussen de winterdijk droog. Alleen als het water in de IJssel bij Zutphen-Noord een hoogte van +8 meter bereikt, zullen de afgravingen in de kades overstromen. In deze folder leest u wat u kan doen als het gebied waarin u woont, dreigt te overstromen. En welke hulp u van de gemeente mag verwachten. We hebben dan immers een gezamenlijke verantwoordelijkheid. De gemeente waarschuwt als u zich op een evacuatie moet voorbereiden. Als de omstandigheden daarna echt kritisch worden, krijgt u een dringend advies om te evacueren. Wilt u toch thuis blijven? Dat mag natuurlijk. Punt van aandacht is wel dat het risico dan ook bij u ligt.
    [Show full text]
  • Travelling by Train with NS All the Information You Need About Your Journey by Train Table of Contents
    Travelling by train with NS All the information you need about your journey by train Table of contents Find the information you need. Welcome 3 Hiring a car at Sprinters and the station 13 Intercitys 22 Preparation 4 Sprinter 22 OV-chipkaart 4 Railway map 14 Intercity 22 It’s easy to take care Standard facilities 22 of it all online 5 The ticket machines 16 Free WiFi 22 View the details of Keuzedagen your trip with Mijn NS 5 (Optional Days) 17 Rules for travel 23 Planning your trip 5 Group travel at a Zones in the Intercity 23 Explore stations discount 17 Baggage, strollers digitally 6 Travelling with and bicycles 23 children 17 Departures 23 Season Tickets 7 Pets on the train 18 Keeping the area Which type of clean 24 traveller are you? 7 Bicycles on the train 18 Smoking 24 Ordering Season Travel information 18 Tickets 7 Checking out 25 Holidays 8 Checking in 19 Forgot to check out? 25 Bijabonnement 8 Why it’s necessary NS-Business Card 8 to check in and out 19 Delay? Money back! 26 Where can you How to request a Individual tickets check in? 19 refund 26 and supplements 9 International travel 1. Single-use chipkaart 9 and e-tickets 20 Lost something? 27 2. Special promotions 9 Have you checked in Lost or stolen 3. Extra comfort 9 successfully? 20 OV-chipkaart? 27 Seeing someone off NS Season Tickets 10 or making a purchase 20 Changing trains/ Getting to and connections 20 from the station 12 By bicycle 12 Assistance at the By car 12 station 21 Continue your journey Our employees 21 with the OV-fiets 12 Safety 21 The convenience of the NS Zonetaxi 13 2 Travelling by train with NS Welcome You are planning to travel by train.
    [Show full text]
  • Circular Buildings the Urban Living Lab Way a Practical Facilitation Tool As Guidance for a Circular Building Process As Collaborative Ecosystem
    Circular Buildings the Urban Living Lab Way A Practical Facilitation Tool as Guidance for a Circular Building Process as Collaborative Ecosystem Quinton Jie MSc Thesis Industrial Ecology Circular Buildings the Urban Living Lab Way A Practical Facilitation Tool as Guidance for a Circular Building Process as Collaborative Ecosystem Thesis Research Project by Quinton Jie Leiden University: S1326589 | Delft University of Technology: 4281799 In partial fulfilment of the requirements for the degree of Master of Science in Industrial Ecology Date of Submission: February 3, 2016 First Supervisor : Dr. Nancy M.P. Bocken, Faculty of Industrial Design Engineering, Delft University of Technology Second Supervisor : Dr. ir. Jaco N. Quist, Faculty of Technology, Policy and Management, Delft University of Technology External Supervisor : Douwe Jan Joustra, Director of ICE-Amsterdam (Implement Circular Economy Amsterdam) Contact : [email protected] Cover Image: “Home symbol with chimney made from jigsaw puzzle pieces”, retrieved from https://www.flickr.com/photos/horiavarlan/4640819987 Executive Summary The built environment is a major contributor to current global problems of resource depletion, pollution and climate change. It is an energy and material intensive sector that relies on the availability of resources. It is an environment where multiple human activities come together that can have their direct and/or indirect impacts within its environment in which the three pillars of sustainability (i.e. People, Planet, Profit) are present. In the case of the Dutch building sector, here presents a challenge, as it is currently highly reliant on the importation of these materials. The concept of Circular Economy introduces new opportunities to become increasingly innovative and becoming more material efficient.
    [Show full text]